2021—2022学年华东师大版数学八年级上册13.4尺规作图 课件 (共32张PPT)
文档属性
| 名称 | 2021—2022学年华东师大版数学八年级上册13.4尺规作图 课件 (共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 20:14:27 | ||
图片预览








文档简介
(共32张PPT)
基本概念
在几何里,把限定用直尺和圆规来画图,称为尺规作图.
要求:直尺是没有刻度的;
只能用没有刻度的直尺和圆规这两种工具来作图,称为尺规作图.
圆规的功能:
以一点为圆心,一定长度为半径作一个圆;以一点为圆心,一定长度为半径画一段弧.
直尺的功能:
在两点间连结一条线段;将线段向一方或两方延长;作直线(三角尺只能当作直尺用)
尺规作图的步骤及作图语言的规范
(3)作法:
根据作图的过程写出每一步的操作过程.当不要求写作法时,要保留作图痕迹.对于较复杂的作图,可先画出草图,使它同所要作的图形大致相同,然后借助草图寻找作法.
(1)已知:
当作图题是用文字语言叙述的,要根据文字语言用数学语言写出题目中的条件;
(2)求作:
根据题目写出要求作出的图形及此图形应满足的条件;
1.尺规作图的步骤
(3)在××上截取一点×,使××=××.
2.作图语言的规范叙述
用直尺作图时的规范语言主要有:
(2)连结××,以点×为端点作线段××,延长线段××到点×;延长线段××到点×,使××=××.
(1)过点×作直线××,作线段××,以点×为端点作射线××;
用圆规作图时的规范语言主要有:
(1)以点×为圆心,××为半径作圆;
(2)以点×为圆心,××为半径作弧交××于点×;
下面就介绍五种基本作图:
一些复杂的尺规作图都是由基本作图组成的.以前学过的”作一条线段等于已知线段”,就是一种基本作图.
最基本,最常用的尺规作图,通常称基本作图.
1、作一条线段等于已知线段
2、作一个角等于已知角
3、平分已知角
4、作已知线段的垂直平分线
5、过一点作已知直线的垂线
五种基本作图:
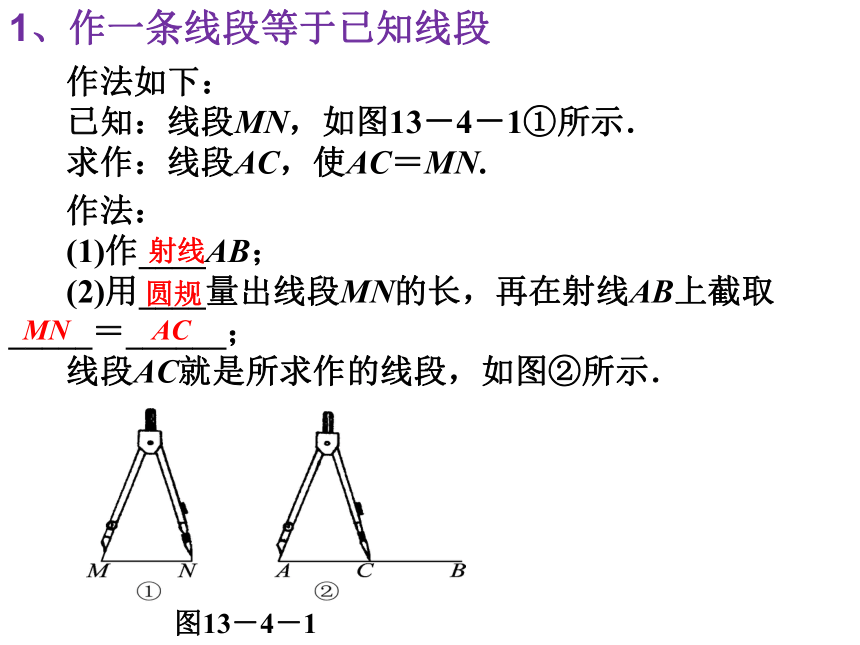
1、作一条线段等于已知线段
AC
射线
圆规
MN
作法:
(1)作____AB;
(2)用____量出线段MN的长,再在射线AB上截取 _____=______;
线段AC就是所求作的线段,如图②所示.
作法如下:
已知:线段MN,如图13-4-1①所示.
求作:线段AC,使AC=MN.
图13-4-1
例1 如图13-4-3所示,已知线段AB和CD,求作一条线段,使它的长度等于2AB+CD.
图13-4-3
[归纳总结] 步骤:
(1)先画一条射线;
(2)在射线上用圆规截取相应的线段,求和时顺次截取叠加,求差时从线段中截取;
(3)指明所作的线段是哪一段,并用字母表示.
注意:
画射线用直尺,截取线段用圆规,作图时要正确使用作图工具,尽量减小误差,用铅笔作图,保留作图痕迹.
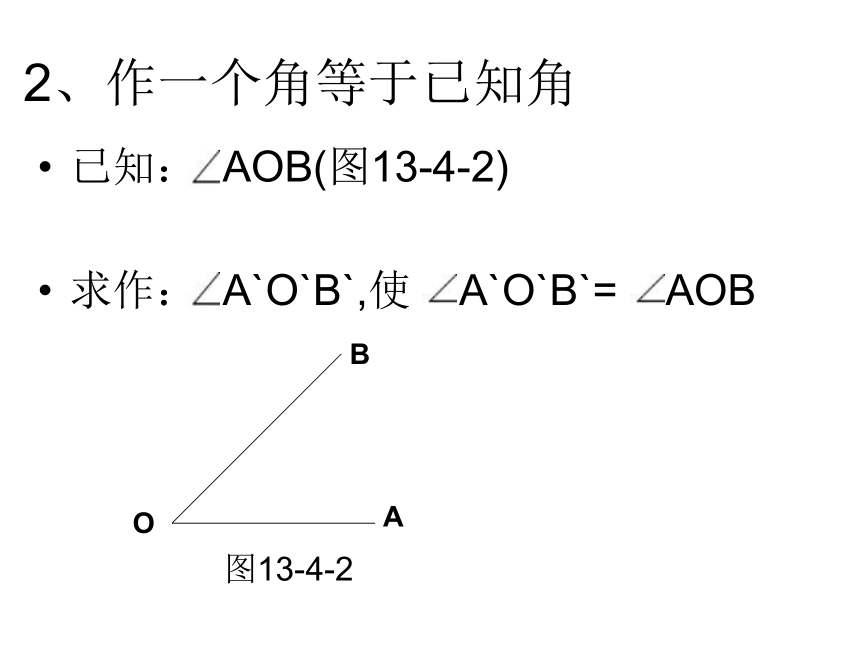
2、作一个角等于已知角
已知: AOB(图13-4-2)
求作: A`O`B`,使 A`O`B`= AOB
O
A
B
图13-4-2
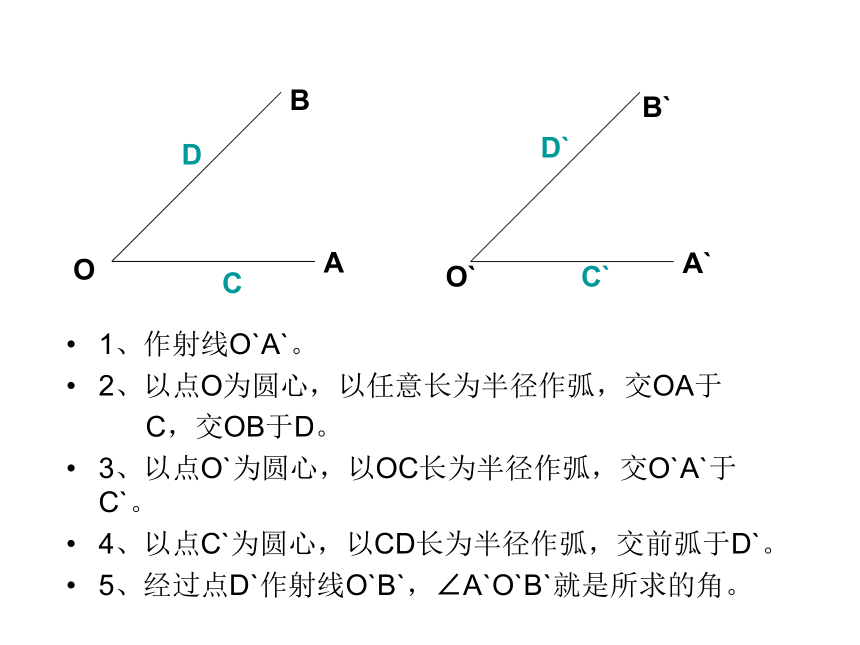
1、作射线O`A`。
2、以点O为圆心,以任意长为半径作弧,交OA于
C,交OB于D。
3、以点O`为圆心,以OC长为半径作弧,交O`A`于 C`。
4、以点C`为圆心,以CD长为半径作弧,交前弧于D`。
5、经过点D`作射线O`B`,∠A`O`B`就是所求的角。
O
A
B
C
D
O`
A`
C`
D`
B`
证明:连结CD、C’D’ ,由作法可知
△C`O`D`≌△COD(SSS),
∴∠C`O`D`=∠COD(全等三角形的对应角相等),
即∠A`O`B`=∠AOB。
O
A
B
C
D
B`
O`
A`
C`
D`
13.4.1 作一条线段等于已知线段 13.4.2 作一个角等于已知角
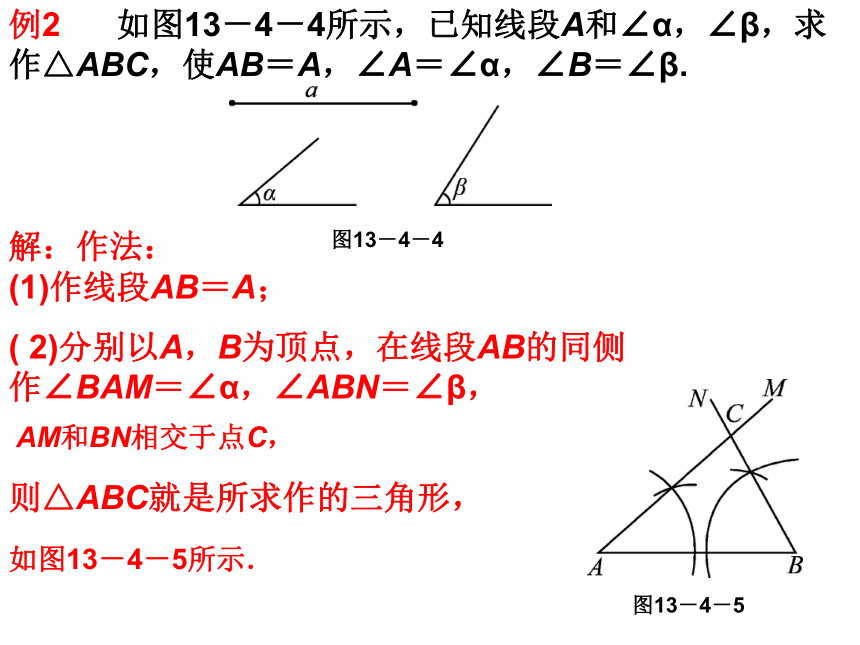
例2 如图13-4-4所示,已知线段A和∠α,∠β,求作△ABC,使AB=A,∠A=∠α,∠B=∠β.
解:作法:
(1)作线段AB=A;
图13-4-5
图13-4-4
( 2)分别以A,B为顶点,在线段AB的同侧作∠BAM=∠α,∠ABN=∠β,
AM和BN相交于点C,
则△ABC就是所求作的三角形,
如图13-4-5所示.
13.4.1 作一条线段等于已知线段 13.4.2 作一个角等于已知角
[归纳总结] 注意:
(1)求作两角和或差时,一定要注明“外部”或“内部”;
(2)求作三角形,一般情况下先作线段再作角,并结合全等三角形的判定方法作图;
(3)本题实质是已知两角及其夹边作三角形.由“角边角”定理,在此条件下所作的三角形是唯一的.
一般情况下先作线段,再作两个角,必须指明在线段的同侧,否则不会相交.基本作图的“作法”不必再详说,如作线段AB的步骤,作∠BAM=∠α的步骤,但必须保留作图痕迹.
3、平分已知角
已知: AOB(图13-4-5)
求作:射线OC,使 AOC= BOC
A
O
B
图13-4-5
1、在OA和OB上,分别截取OD、OE,使OD=OE。
2、分别以D、E为圆心,大于DE的长为半径作弧,在∠AOB内,两弧交于点C。
3、作射线OC。
4、OC就是所求的射线。
A
O
B
C
D
E
例3 如图13-4-6所示,作出△ABC三个内角的平分线,并观察你作出的图形,有什么新的发现?
解:发现三条内角平分线相交于同一点.
[归纳总结]
(1)作已知角的平分线,是根据“三边对应相等的两个三角形全等”和“全等三角形的对应角相等”的原理来解决的.
(2)在作图步骤的第二步一定要注意是以大于某条线段的1/2长为半径作圆弧的,否则两弧没有交点或两弧交点不明显.
(3)通过作图了解三角形三个内角的平分线相交于一点.
图13-4-6
13.4.3 作已知角的平分线
例4 如图13-4-7所示,已知∠CAB,以确定的点B为顶点作∠ABD,使∠ABD=∠A.(不写作法,保留作图痕迹)
图13-4-7
[解析] 先作∠A的平分线AE,以B为顶点作∠ABD=∠EAB,则∠ABD即为所求.
图13-4-8
解:如图13-4-8所示
[归纳总结]
作一个角等于已知角是属于定量作图,而作角的平分线则是属于定位作图.在综合作图题中,有时既需要定量,又需要定位.
4、画已知线段的垂直平分线
定义:
于一条线段并且 这条线段的直线,叫做线段的垂直平分线(或叫中垂线).
已知:线段AB,
求作:作直线CD交AB于O,使CD⊥AB,AO=BO.
垂直
平分
步骤:
1、以点A为圆心,以大于AB一半的长为半径画弧;
2、以点B为圆心,以同样的长为半径画弧,
两弧的交点分别记为C、D,连结CD,则CD是线段AB的垂直平分线.
例5 如图13-4-9所示,
作△ABC的边BC上的高.
图13-4-9
解:即过A点作直线BC的垂线,垂线段即为高,如图13-4-10中线段AF即为所求.
图13-4-10
[归纳总结] 作三角形的高是作垂线的简单运用.由于钝角三角形有两条高是在三角形的外部,所以作图时要注意延长三角形的边,保留痕迹.
例6 如图13-4-11所示,已知线段AB和线段CD,求作一点P,使点P既在线段AB的垂直平分线上,又在线段CD的垂直平分线上.
图13-4-11
解:(1)作线段AB的垂直平分线EF;
(2)作线段CD的垂直平分线MN,MN交EF于点P.
则点P就是所求作的点,
如图13-4-12.
图13-4-12
5.过定点作已知直线的垂线
①.如图,点C在直线l上,试过点C画出直线l的垂线.
能否利用画线段垂直平分线的方法解决呢?试试看,完成整个作图.
以C为圆心,任一线段的长为半径画弧,交l于A、B两点,则C是线段AB的中点.因此,过C画直线l的垂线转化为画线段AB的垂直平分线.
②.如图,如果点C不在直线l上,试和同学讨论,应采取怎样的步骤,过点C画出直线l的垂线?
作法:(1)以点C为圆心,任一线段的长为半径画弧,交直线l于点A、B;
(3)以点B为圆心,以同样的长为半径在直线的同一侧画弧,两弧交于点D;
(4)经过点C、D作直线CD.
(2)以A为圆心,以大于CB长为半径在直线一侧画弧;
①.如图,点C在直线l上,试过点C画出直线l的垂线.
(4)经过点C、D作直线CD.
(3)以点B为圆心,以CB长为半径在直线另一侧画弧,交前一条弧于点D.
作法:(1)以点C为圆心,以适当长为半径画弧,交直线l于点A、B;
(2)以点A为圆心,以CB长为半径在直线另一侧画弧.
②.如图,如果点C不在直线l上,试和同学讨论,应采取怎样的步骤,过点C画出直线l的垂线?
例7 如图13-4-13所示,过点P作∠A两边的垂线.
图13-4-13
[解析] 此题即为过直线外一点作直线的垂线.
解:如图所示,PM,PN即为所求作的直线.
[归纳总结]
(1)过直线上一点作垂线即作出平角的平分线.
(2)过直线外一点作垂线,利用等腰三角形“三线合一”的性质.
(3)作“高”即过直线外一点作已知直线的垂线,垂线段即为高.
如图,已知∠AOB及M、N两点,求作:点P,使点P到∠AOB的两边距离相等,且到M、N的两点也距离相等。
练习
生活离不开数学
A、B是两个村庄,要从灌溉总渠引两条水渠便于灌溉,请你选择最佳方案。
已知:线段a,c,∠α
求作:ΔABC,使BC=a,AB=c,∠ABC=∠ α
作法:1)作一条线段BC=a
2)以B为顶点,BC为一边,作,∠DBC=∠ α
3)在射线BD上截取线段BA=c
4)连接AC, ΔABC就是所求作的三角形
a
c
α
探索研究:
2、三条公路两两相交,交点分别为A,B,C,现计划建一个加油站,要求到三条公路的距离相等,问满足要求的加油站地址有几种情况?
A
B
C
?五种基本作图
(1)作一条线段等于已知线段
(2)作一个角等于已知角
小结
(3)作一个角的平分线
(4)作已知线段的中垂线
(5)过一点作已知直线的垂线
基本概念
在几何里,把限定用直尺和圆规来画图,称为尺规作图.
要求:直尺是没有刻度的;
只能用没有刻度的直尺和圆规这两种工具来作图,称为尺规作图.
圆规的功能:
以一点为圆心,一定长度为半径作一个圆;以一点为圆心,一定长度为半径画一段弧.
直尺的功能:
在两点间连结一条线段;将线段向一方或两方延长;作直线(三角尺只能当作直尺用)
尺规作图的步骤及作图语言的规范
(3)作法:
根据作图的过程写出每一步的操作过程.当不要求写作法时,要保留作图痕迹.对于较复杂的作图,可先画出草图,使它同所要作的图形大致相同,然后借助草图寻找作法.
(1)已知:
当作图题是用文字语言叙述的,要根据文字语言用数学语言写出题目中的条件;
(2)求作:
根据题目写出要求作出的图形及此图形应满足的条件;
1.尺规作图的步骤
(3)在××上截取一点×,使××=××.
2.作图语言的规范叙述
用直尺作图时的规范语言主要有:
(2)连结××,以点×为端点作线段××,延长线段××到点×;延长线段××到点×,使××=××.
(1)过点×作直线××,作线段××,以点×为端点作射线××;
用圆规作图时的规范语言主要有:
(1)以点×为圆心,××为半径作圆;
(2)以点×为圆心,××为半径作弧交××于点×;
下面就介绍五种基本作图:
一些复杂的尺规作图都是由基本作图组成的.以前学过的”作一条线段等于已知线段”,就是一种基本作图.
最基本,最常用的尺规作图,通常称基本作图.
1、作一条线段等于已知线段
2、作一个角等于已知角
3、平分已知角
4、作已知线段的垂直平分线
5、过一点作已知直线的垂线
五种基本作图:
1、作一条线段等于已知线段
AC
射线
圆规
MN
作法:
(1)作____AB;
(2)用____量出线段MN的长,再在射线AB上截取 _____=______;
线段AC就是所求作的线段,如图②所示.
作法如下:
已知:线段MN,如图13-4-1①所示.
求作:线段AC,使AC=MN.
图13-4-1
例1 如图13-4-3所示,已知线段AB和CD,求作一条线段,使它的长度等于2AB+CD.
图13-4-3
[归纳总结] 步骤:
(1)先画一条射线;
(2)在射线上用圆规截取相应的线段,求和时顺次截取叠加,求差时从线段中截取;
(3)指明所作的线段是哪一段,并用字母表示.
注意:
画射线用直尺,截取线段用圆规,作图时要正确使用作图工具,尽量减小误差,用铅笔作图,保留作图痕迹.
2、作一个角等于已知角
已知: AOB(图13-4-2)
求作: A`O`B`,使 A`O`B`= AOB
O
A
B
图13-4-2
1、作射线O`A`。
2、以点O为圆心,以任意长为半径作弧,交OA于
C,交OB于D。
3、以点O`为圆心,以OC长为半径作弧,交O`A`于 C`。
4、以点C`为圆心,以CD长为半径作弧,交前弧于D`。
5、经过点D`作射线O`B`,∠A`O`B`就是所求的角。
O
A
B
C
D
O`
A`
C`
D`
B`
证明:连结CD、C’D’ ,由作法可知
△C`O`D`≌△COD(SSS),
∴∠C`O`D`=∠COD(全等三角形的对应角相等),
即∠A`O`B`=∠AOB。
O
A
B
C
D
B`
O`
A`
C`
D`
13.4.1 作一条线段等于已知线段 13.4.2 作一个角等于已知角
例2 如图13-4-4所示,已知线段A和∠α,∠β,求作△ABC,使AB=A,∠A=∠α,∠B=∠β.
解:作法:
(1)作线段AB=A;
图13-4-5
图13-4-4
( 2)分别以A,B为顶点,在线段AB的同侧作∠BAM=∠α,∠ABN=∠β,
AM和BN相交于点C,
则△ABC就是所求作的三角形,
如图13-4-5所示.
13.4.1 作一条线段等于已知线段 13.4.2 作一个角等于已知角
[归纳总结] 注意:
(1)求作两角和或差时,一定要注明“外部”或“内部”;
(2)求作三角形,一般情况下先作线段再作角,并结合全等三角形的判定方法作图;
(3)本题实质是已知两角及其夹边作三角形.由“角边角”定理,在此条件下所作的三角形是唯一的.
一般情况下先作线段,再作两个角,必须指明在线段的同侧,否则不会相交.基本作图的“作法”不必再详说,如作线段AB的步骤,作∠BAM=∠α的步骤,但必须保留作图痕迹.
3、平分已知角
已知: AOB(图13-4-5)
求作:射线OC,使 AOC= BOC
A
O
B
图13-4-5
1、在OA和OB上,分别截取OD、OE,使OD=OE。
2、分别以D、E为圆心,大于DE的长为半径作弧,在∠AOB内,两弧交于点C。
3、作射线OC。
4、OC就是所求的射线。
A
O
B
C
D
E
例3 如图13-4-6所示,作出△ABC三个内角的平分线,并观察你作出的图形,有什么新的发现?
解:发现三条内角平分线相交于同一点.
[归纳总结]
(1)作已知角的平分线,是根据“三边对应相等的两个三角形全等”和“全等三角形的对应角相等”的原理来解决的.
(2)在作图步骤的第二步一定要注意是以大于某条线段的1/2长为半径作圆弧的,否则两弧没有交点或两弧交点不明显.
(3)通过作图了解三角形三个内角的平分线相交于一点.
图13-4-6
13.4.3 作已知角的平分线
例4 如图13-4-7所示,已知∠CAB,以确定的点B为顶点作∠ABD,使∠ABD=∠A.(不写作法,保留作图痕迹)
图13-4-7
[解析] 先作∠A的平分线AE,以B为顶点作∠ABD=∠EAB,则∠ABD即为所求.
图13-4-8
解:如图13-4-8所示
[归纳总结]
作一个角等于已知角是属于定量作图,而作角的平分线则是属于定位作图.在综合作图题中,有时既需要定量,又需要定位.
4、画已知线段的垂直平分线
定义:
于一条线段并且 这条线段的直线,叫做线段的垂直平分线(或叫中垂线).
已知:线段AB,
求作:作直线CD交AB于O,使CD⊥AB,AO=BO.
垂直
平分
步骤:
1、以点A为圆心,以大于AB一半的长为半径画弧;
2、以点B为圆心,以同样的长为半径画弧,
两弧的交点分别记为C、D,连结CD,则CD是线段AB的垂直平分线.
例5 如图13-4-9所示,
作△ABC的边BC上的高.
图13-4-9
解:即过A点作直线BC的垂线,垂线段即为高,如图13-4-10中线段AF即为所求.
图13-4-10
[归纳总结] 作三角形的高是作垂线的简单运用.由于钝角三角形有两条高是在三角形的外部,所以作图时要注意延长三角形的边,保留痕迹.
例6 如图13-4-11所示,已知线段AB和线段CD,求作一点P,使点P既在线段AB的垂直平分线上,又在线段CD的垂直平分线上.
图13-4-11
解:(1)作线段AB的垂直平分线EF;
(2)作线段CD的垂直平分线MN,MN交EF于点P.
则点P就是所求作的点,
如图13-4-12.
图13-4-12
5.过定点作已知直线的垂线
①.如图,点C在直线l上,试过点C画出直线l的垂线.
能否利用画线段垂直平分线的方法解决呢?试试看,完成整个作图.
以C为圆心,任一线段的长为半径画弧,交l于A、B两点,则C是线段AB的中点.因此,过C画直线l的垂线转化为画线段AB的垂直平分线.
②.如图,如果点C不在直线l上,试和同学讨论,应采取怎样的步骤,过点C画出直线l的垂线?
作法:(1)以点C为圆心,任一线段的长为半径画弧,交直线l于点A、B;
(3)以点B为圆心,以同样的长为半径在直线的同一侧画弧,两弧交于点D;
(4)经过点C、D作直线CD.
(2)以A为圆心,以大于CB长为半径在直线一侧画弧;
①.如图,点C在直线l上,试过点C画出直线l的垂线.
(4)经过点C、D作直线CD.
(3)以点B为圆心,以CB长为半径在直线另一侧画弧,交前一条弧于点D.
作法:(1)以点C为圆心,以适当长为半径画弧,交直线l于点A、B;
(2)以点A为圆心,以CB长为半径在直线另一侧画弧.
②.如图,如果点C不在直线l上,试和同学讨论,应采取怎样的步骤,过点C画出直线l的垂线?
例7 如图13-4-13所示,过点P作∠A两边的垂线.
图13-4-13
[解析] 此题即为过直线外一点作直线的垂线.
解:如图所示,PM,PN即为所求作的直线.
[归纳总结]
(1)过直线上一点作垂线即作出平角的平分线.
(2)过直线外一点作垂线,利用等腰三角形“三线合一”的性质.
(3)作“高”即过直线外一点作已知直线的垂线,垂线段即为高.
如图,已知∠AOB及M、N两点,求作:点P,使点P到∠AOB的两边距离相等,且到M、N的两点也距离相等。
练习
生活离不开数学
A、B是两个村庄,要从灌溉总渠引两条水渠便于灌溉,请你选择最佳方案。
已知:线段a,c,∠α
求作:ΔABC,使BC=a,AB=c,∠ABC=∠ α
作法:1)作一条线段BC=a
2)以B为顶点,BC为一边,作,∠DBC=∠ α
3)在射线BD上截取线段BA=c
4)连接AC, ΔABC就是所求作的三角形
a
c
α
探索研究:
2、三条公路两两相交,交点分别为A,B,C,现计划建一个加油站,要求到三条公路的距离相等,问满足要求的加油站地址有几种情况?
A
B
C
?五种基本作图
(1)作一条线段等于已知线段
(2)作一个角等于已知角
小结
(3)作一个角的平分线
(4)作已知线段的中垂线
(5)过一点作已知直线的垂线
