2021-2022学年华东师大版九年级数学上册24.3 锐角三角函数课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学上册24.3 锐角三角函数课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 20:22:12 | ||
图片预览





文档简介
(共21张PPT)
解直角三角形
------锐角三角函数
∠A的邻边b
A
C
B
∠A的对边a
斜边c
知识点1:直角三角形的认识
1:对于∠A来说:
2:对于∠B来说,它们分别是什么?
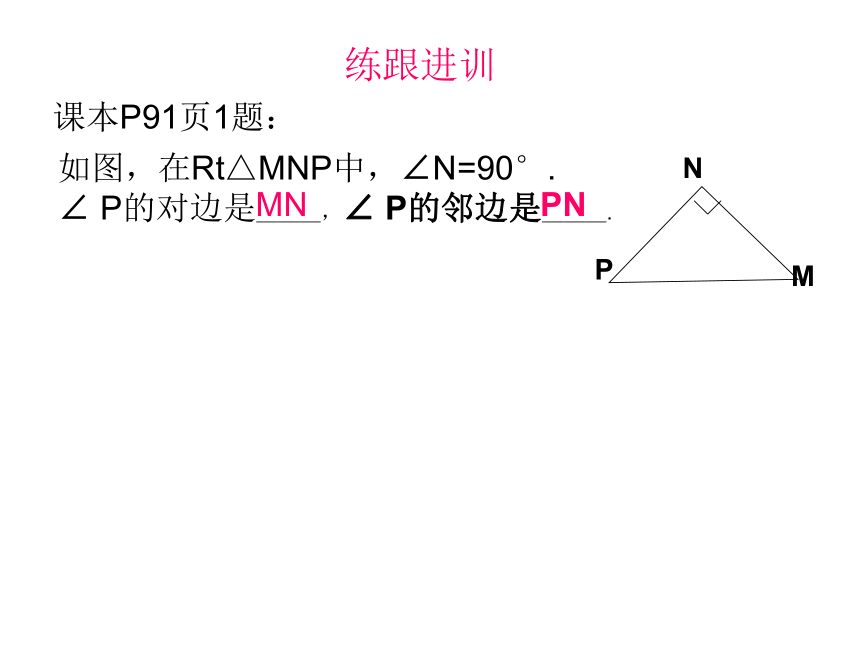
练跟进训
课本P91页1题:
如图,在Rt△MNP中,∠N=90°.
∠ P的对边是___,∠ P的邻边是___.
N
P
M
MN
PN
思考:在Rt△AB3C3中,当锐角A取其它的固定值的时候,∠A的对边与邻边的比值还会是一个固定值吗?
A
B3
C3
C1
C2
B2
B1
分析:易知 Rt△AB1C1∽
Rt△AB2C2 ∽ Rt△AB3C3
∴
可见:在Rt△ABC中,对于锐角A的每一个确定的值,它的对边与邻边的比值是一个定值。实际上,对边与斜边、邻边与斜边的比值也是一个定值。
知识点2:锐角三角函数定义
1、∠A的对边与斜边的比值叫做∠A的正弦,记作sinA,
即
2、∠A的邻边与斜边的比值叫做∠A的余弦,记作cosA,
即
3、∠A的对边与邻边的比值叫做∠A的正切,记作tanA,即
4、∠A的邻边与对边的比值叫做∠A的余切,记作cotA,
即
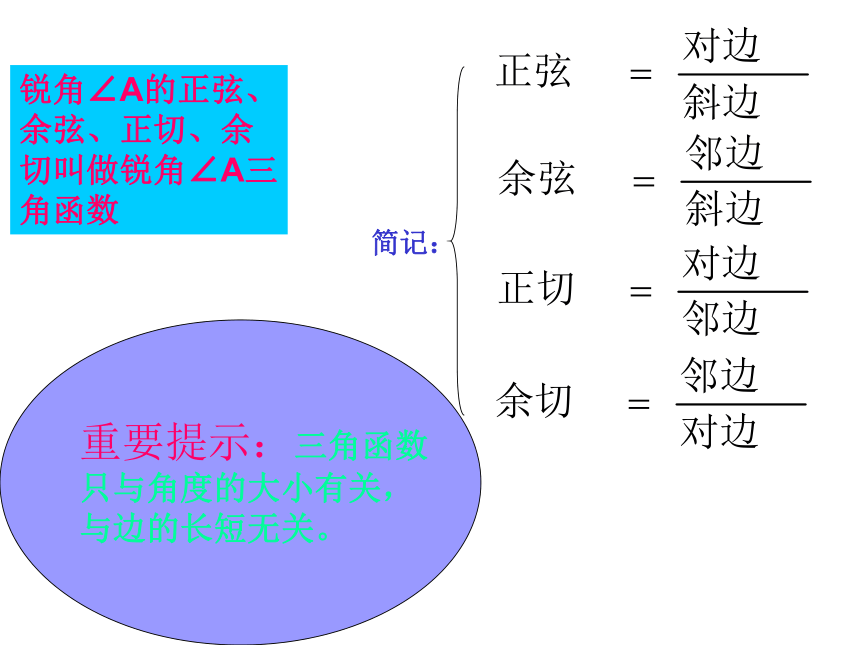
锐角∠A的正弦、余弦、正切、余切叫做锐角∠A三角函数
简记:
重要提示:三角函数
只与角度的大小有关,
与边的长短无关。
锐角三角函数定义
正弦,余弦,正切,余切:
回顾与思考
1
驶向胜利的彼岸
b
A
B
C
a
┌
c
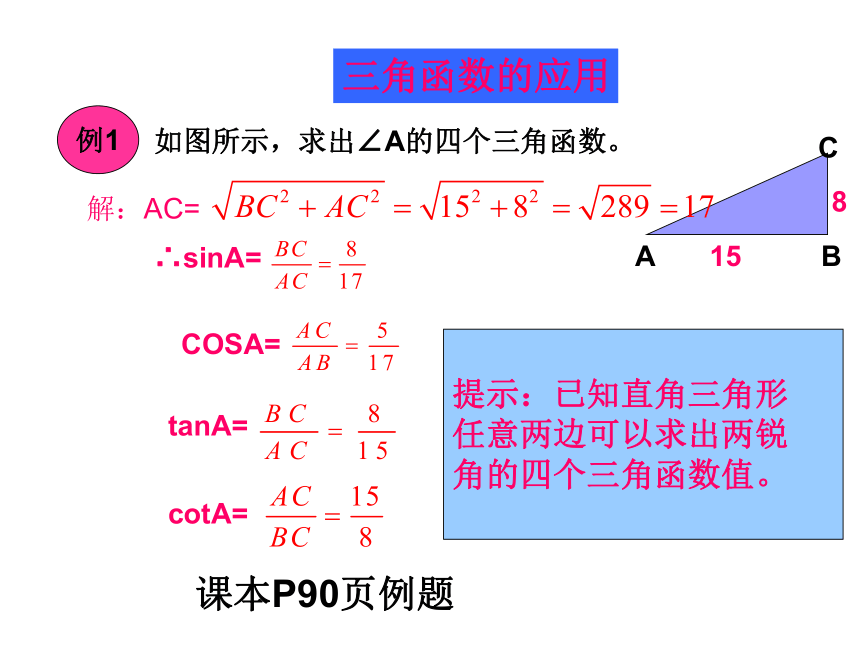
三角函数的应用
例1
如图所示,求出∠A的四个三角函数。
A
B
C
15
8
解:AC=
∴sinA=
COSA=
tanA=
cotA=
提示:已知直角三角形
任意两边可以求出两锐
角的四个三角函数值。
课本P90页例题
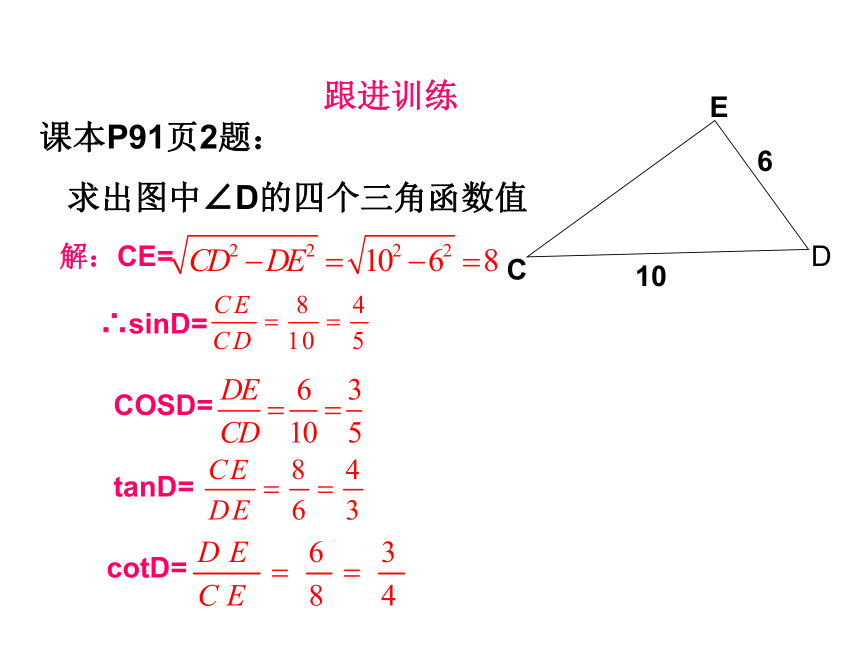
跟进训练
课本P91页2题:
求出图中∠D的四个三角函数值
C
D
E
10
6
解:CE=
∴sinD=
COSD=
tanD=
cotD=
例2
如图所示,在△ABC中,AB=AC=13,cosB=
则BC=__________。
A
B
C
D
分析:三角函数是在直角三角形中,而题中没有直角三角形,所以,需要作辅助线,将∠B放入一个直角三角形中。
∵cosB=
∴
∴BD=5,
∴BC=
2BD=10
10
跟进训练
在Rt△ABC中,∠B=90°,sinC= 求∠A的四个三角函数值。
解:∵sinC=
分析:∠B=90°,则斜边应为AC
B
C
A
AB:AC=5:13
∴可设AB= 。AC= 。
5k
13k
5k
13k
∴BC=
12k
∴sinA=
COSA=
tanA=
cotA=
方法总结:已知一个三角函数值,相当于已知两边的比,设每一份为k,求出第三边,然后根据三角函数的定义就可求出其它三角函数值
知识点3:三角函数的性质
1:取值范围:
A
C
B
0<sinA<1
0<cosA<1
tanA>0
cotA>0
a
b
c
∵a<c,b<c,且a、b、c都大于0
2.互余两角之间的三角函数关系:
直角三角形两锐角互余:∠A+∠B=900.
则∠B=90°- ∠A
b
A
B
C
a
┌
c
则 sinA=cosB或cosA=sinB.
tanA=cotB或cotA=tanB.
sinA=cos(90°-A) 或cosA=sin (90°-A). tanA=cot (90°-A)或cotA=tan (90°-A).
一个角的正弦等于它的余角的余弦;一个角的余弦等于它的余角的正弦;一个角的正切等于它的余角的余切;一个角的余切等于它的余角的正切。
强化训练
1、sin30°= 则cos60°=______.
2、tan60°= 则cot30°=______.
3、cosA=0.32, 则__________=0.32
Sin(90°-A)
3.同角之间的三角函数的关系
(1)平方和关系:
b
A
B
C
a
┌
c
(2)商的关系:
(3)倒数关系:
例3
已知sinA= ,求∠A的其他三个三角函数值
解:cosA=
tanA=
cotA=
∵sinA=a:c,
∴可设a=k,
C=3k,由勾股
定理可求出b,
然后根据定义
求出其他三个
三角函数值可
跟进训练
拓展训练
∴可设_______=5k,_______12k
又∵ =1
知识点4:直角三角形的性质
这个结论你知道是如何得出的吗?
理由如下:过点C作AB边上的中线CD
B
C
A
D
∵∠ACB=900
∴AD=CD=BD
∵∠B=300
∴∠DCB=300
∴∠ACD=600
∴△ACD是等边三角形
∴AC=AD=
小结
sinA=cos(90°-A) 或cosA=sin (90°-A). tanA=cot (90°-A)或cotA=tan (90°-A).
b
A
B
C
a
┌
c
1.直角三角形三边的关系:
2.直角三角形两锐角的关系:
∠A+∠B=90°.
3.直角三角形边与角之间的关系:
4、互为余角的三角函数间的关系:
5、同角之间的三角函数关系:
6、直角三角形30°所对直角边的性质:
作业
课本P93页习题25.2 1 、 2题
补充
1:在Rt△ABC中,∠C=90°,斜边AB是直角边 AC的3倍。求∠A的四个三角函数值
2:已知sinA= ,求∠A的另外三个三角函数值
解直角三角形
------锐角三角函数
∠A的邻边b
A
C
B
∠A的对边a
斜边c
知识点1:直角三角形的认识
1:对于∠A来说:
2:对于∠B来说,它们分别是什么?
练跟进训
课本P91页1题:
如图,在Rt△MNP中,∠N=90°.
∠ P的对边是___,∠ P的邻边是___.
N
P
M
MN
PN
思考:在Rt△AB3C3中,当锐角A取其它的固定值的时候,∠A的对边与邻边的比值还会是一个固定值吗?
A
B3
C3
C1
C2
B2
B1
分析:易知 Rt△AB1C1∽
Rt△AB2C2 ∽ Rt△AB3C3
∴
可见:在Rt△ABC中,对于锐角A的每一个确定的值,它的对边与邻边的比值是一个定值。实际上,对边与斜边、邻边与斜边的比值也是一个定值。
知识点2:锐角三角函数定义
1、∠A的对边与斜边的比值叫做∠A的正弦,记作sinA,
即
2、∠A的邻边与斜边的比值叫做∠A的余弦,记作cosA,
即
3、∠A的对边与邻边的比值叫做∠A的正切,记作tanA,即
4、∠A的邻边与对边的比值叫做∠A的余切,记作cotA,
即
锐角∠A的正弦、余弦、正切、余切叫做锐角∠A三角函数
简记:
重要提示:三角函数
只与角度的大小有关,
与边的长短无关。
锐角三角函数定义
正弦,余弦,正切,余切:
回顾与思考
1
驶向胜利的彼岸
b
A
B
C
a
┌
c
三角函数的应用
例1
如图所示,求出∠A的四个三角函数。
A
B
C
15
8
解:AC=
∴sinA=
COSA=
tanA=
cotA=
提示:已知直角三角形
任意两边可以求出两锐
角的四个三角函数值。
课本P90页例题
跟进训练
课本P91页2题:
求出图中∠D的四个三角函数值
C
D
E
10
6
解:CE=
∴sinD=
COSD=
tanD=
cotD=
例2
如图所示,在△ABC中,AB=AC=13,cosB=
则BC=__________。
A
B
C
D
分析:三角函数是在直角三角形中,而题中没有直角三角形,所以,需要作辅助线,将∠B放入一个直角三角形中。
∵cosB=
∴
∴BD=5,
∴BC=
2BD=10
10
跟进训练
在Rt△ABC中,∠B=90°,sinC= 求∠A的四个三角函数值。
解:∵sinC=
分析:∠B=90°,则斜边应为AC
B
C
A
AB:AC=5:13
∴可设AB= 。AC= 。
5k
13k
5k
13k
∴BC=
12k
∴sinA=
COSA=
tanA=
cotA=
方法总结:已知一个三角函数值,相当于已知两边的比,设每一份为k,求出第三边,然后根据三角函数的定义就可求出其它三角函数值
知识点3:三角函数的性质
1:取值范围:
A
C
B
0<sinA<1
0<cosA<1
tanA>0
cotA>0
a
b
c
∵a<c,b<c,且a、b、c都大于0
2.互余两角之间的三角函数关系:
直角三角形两锐角互余:∠A+∠B=900.
则∠B=90°- ∠A
b
A
B
C
a
┌
c
则 sinA=cosB或cosA=sinB.
tanA=cotB或cotA=tanB.
sinA=cos(90°-A) 或cosA=sin (90°-A). tanA=cot (90°-A)或cotA=tan (90°-A).
一个角的正弦等于它的余角的余弦;一个角的余弦等于它的余角的正弦;一个角的正切等于它的余角的余切;一个角的余切等于它的余角的正切。
强化训练
1、sin30°= 则cos60°=______.
2、tan60°= 则cot30°=______.
3、cosA=0.32, 则__________=0.32
Sin(90°-A)
3.同角之间的三角函数的关系
(1)平方和关系:
b
A
B
C
a
┌
c
(2)商的关系:
(3)倒数关系:
例3
已知sinA= ,求∠A的其他三个三角函数值
解:cosA=
tanA=
cotA=
∵sinA=a:c,
∴可设a=k,
C=3k,由勾股
定理可求出b,
然后根据定义
求出其他三个
三角函数值可
跟进训练
拓展训练
∴可设_______=5k,_______12k
又∵ =1
知识点4:直角三角形的性质
这个结论你知道是如何得出的吗?
理由如下:过点C作AB边上的中线CD
B
C
A
D
∵∠ACB=900
∴AD=CD=BD
∵∠B=300
∴∠DCB=300
∴∠ACD=600
∴△ACD是等边三角形
∴AC=AD=
小结
sinA=cos(90°-A) 或cosA=sin (90°-A). tanA=cot (90°-A)或cotA=tan (90°-A).
b
A
B
C
a
┌
c
1.直角三角形三边的关系:
2.直角三角形两锐角的关系:
∠A+∠B=90°.
3.直角三角形边与角之间的关系:
4、互为余角的三角函数间的关系:
5、同角之间的三角函数关系:
6、直角三角形30°所对直角边的性质:
作业
课本P93页习题25.2 1 、 2题
补充
1:在Rt△ABC中,∠C=90°,斜边AB是直角边 AC的3倍。求∠A的四个三角函数值
2:已知sinA= ,求∠A的另外三个三角函数值
