2021—2022学年华东师大版数学八年级上册第14章勾股定理复习课件 (共14张PPT)
文档属性
| 名称 | 2021—2022学年华东师大版数学八年级上册第14章勾股定理复习课件 (共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 156.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 20:24:44 | ||
图片预览




文档简介
(共14张PPT)
勾股定理复习
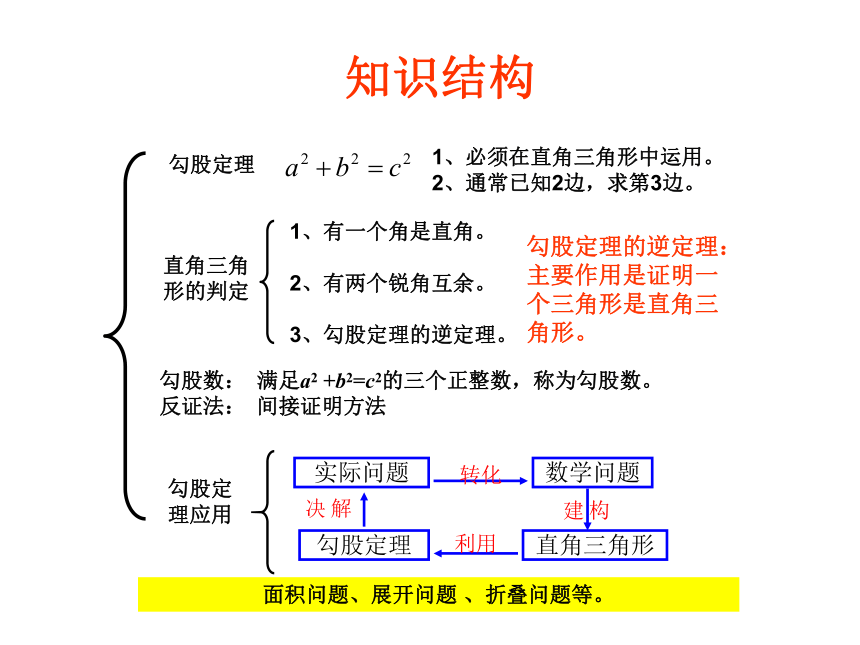
知识结构
勾股定理
1、必须在直角三角形中运用。
2、通常已知2边,求第3边。
直角三角形的判定
1、有一个角是直角。
2、有两个锐角互余。
3、勾股定理的逆定理。
勾股定理的逆定理:主要作用是证明一个三角形是直角三角形。
勾股定理应用
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
解决
勾股数: 满足a2 +b2=c2的三个正整数,称为勾股数。
反证法: 间接证明方法
面积问题、展开问题 、折叠问题等。
本节课重点复习
易错题复习
勾股定理的应用
展开问题
折叠问题
1. ABC的两边AB=5,AC=12,则BC=13 ( )
1 . 对 2. 错
2.直角 ABC中∠B=90°,a=6,b=8,则c=10 ( ) 1 . 对 2. 错
3、已知:数3和4,请你再写一个数,使这些数恰好是一个直角三角形三边长,则这
个数可以是( )
分类思想:
直角三角形中,直角边、斜边不知道时,应分类讨论。
易错题复习
2.重点复习:展开问题和折叠问题.
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
解决
1.
勾股定理的应用
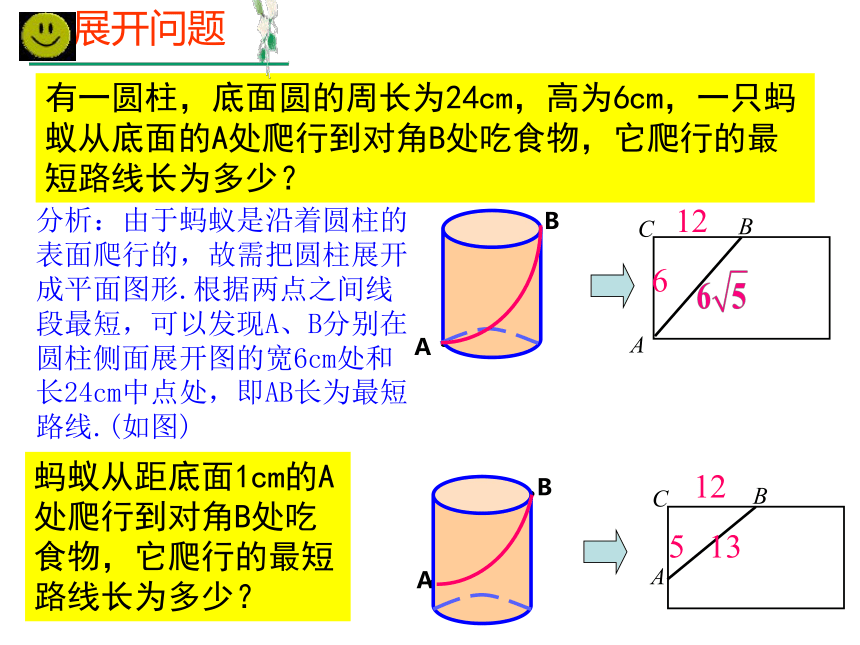
有一圆柱,底面圆的周长为24cm,高为6cm,一只蚂蚁从底面的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?
A
B
B
A
C
蚂蚁从距底面1cm的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?
A
B
B
A
C
展开问题
分析:由于蚂蚁是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽6cm处和长24cm中点处,即AB长为最短路线.(如图)
12
6
12
5
13
A
变式1:
有一木质圆柱形笔筒的高为h,底面半径为r,现要围绕笔筒的表面由A至C,(A,C在圆柱的同一轴截面上)镶入一条银色金属线作为装饰,这条金属线的最短长度是多少?
C
B
A
D
C
A
B
10
10
10
B
C
A
C
变式2:如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面由A至B需要爬行的最短路程又是多少呢?
正方体有六种路线,路程都一样。
变式3:如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
A
B
3
2
1
分析:有3种情况,六条路线。
(1)经过前面和上底面; (或经过后面和下底面)
(2)经过前面和右面; (或经过左面和后面)
(3)经过左面和上底面. (或经过下底面和右面)
A
B
2
3
A
B
1
C
3
2
1
B
C
A
3
2
1
B
C
A
3
2
1
练习1:
一只蚂蚁从实心长方体的顶点A1出发,沿长方体的表面爬到对角顶点C处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?
A
B
A1
B1
D
C
D1
C1
2
1
4
A1
B1
1
4
5
A1
A
4
1
A1
D1
4
2
第一种路线最短
长方体需要讨论分析最短路线
折叠长方形纸片,先折出折痕对角线BD,在绕点D折叠,使点A落在BD的E处,折痕DG,若AB=4,BC=3,求AG的长。
D
A
G
B
C
E
折叠问题
4
x
3
4
3
4-x
x
3
你还能用其他方法求AG的长吗?
折叠长方形纸片,先折出折痕对角线BD,在绕点D折叠,使点A落在BD的E处,折痕DG,若AB=4,BC=3,求AG的长。
D
A
G
B
C
E
拓展延伸
4
x
3
4
3
4-x
x
3
你还能用其他方法求AG的长吗?
2.注意:运用勾股定理解决实际问题,关键在于“找”到合适的直角三角形.
勾股定理的应用
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
解决
1.
勾股定理复习
知识结构
勾股定理
1、必须在直角三角形中运用。
2、通常已知2边,求第3边。
直角三角形的判定
1、有一个角是直角。
2、有两个锐角互余。
3、勾股定理的逆定理。
勾股定理的逆定理:主要作用是证明一个三角形是直角三角形。
勾股定理应用
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
解决
勾股数: 满足a2 +b2=c2的三个正整数,称为勾股数。
反证法: 间接证明方法
面积问题、展开问题 、折叠问题等。
本节课重点复习
易错题复习
勾股定理的应用
展开问题
折叠问题
1. ABC的两边AB=5,AC=12,则BC=13 ( )
1 . 对 2. 错
2.直角 ABC中∠B=90°,a=6,b=8,则c=10 ( ) 1 . 对 2. 错
3、已知:数3和4,请你再写一个数,使这些数恰好是一个直角三角形三边长,则这
个数可以是( )
分类思想:
直角三角形中,直角边、斜边不知道时,应分类讨论。
易错题复习
2.重点复习:展开问题和折叠问题.
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
解决
1.
勾股定理的应用
有一圆柱,底面圆的周长为24cm,高为6cm,一只蚂蚁从底面的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?
A
B
B
A
C
蚂蚁从距底面1cm的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?
A
B
B
A
C
展开问题
分析:由于蚂蚁是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽6cm处和长24cm中点处,即AB长为最短路线.(如图)
12
6
12
5
13
A
变式1:
有一木质圆柱形笔筒的高为h,底面半径为r,现要围绕笔筒的表面由A至C,(A,C在圆柱的同一轴截面上)镶入一条银色金属线作为装饰,这条金属线的最短长度是多少?
C
B
A
D
C
A
B
10
10
10
B
C
A
C
变式2:如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面由A至B需要爬行的最短路程又是多少呢?
正方体有六种路线,路程都一样。
变式3:如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
A
B
3
2
1
分析:有3种情况,六条路线。
(1)经过前面和上底面; (或经过后面和下底面)
(2)经过前面和右面; (或经过左面和后面)
(3)经过左面和上底面. (或经过下底面和右面)
A
B
2
3
A
B
1
C
3
2
1
B
C
A
3
2
1
B
C
A
3
2
1
练习1:
一只蚂蚁从实心长方体的顶点A1出发,沿长方体的表面爬到对角顶点C处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?
A
B
A1
B1
D
C
D1
C1
2
1
4
A1
B1
1
4
5
A1
A
4
1
A1
D1
4
2
第一种路线最短
长方体需要讨论分析最短路线
折叠长方形纸片,先折出折痕对角线BD,在绕点D折叠,使点A落在BD的E处,折痕DG,若AB=4,BC=3,求AG的长。
D
A
G
B
C
E
折叠问题
4
x
3
4
3
4-x
x
3
你还能用其他方法求AG的长吗?
折叠长方形纸片,先折出折痕对角线BD,在绕点D折叠,使点A落在BD的E处,折痕DG,若AB=4,BC=3,求AG的长。
D
A
G
B
C
E
拓展延伸
4
x
3
4
3
4-x
x
3
你还能用其他方法求AG的长吗?
2.注意:运用勾股定理解决实际问题,关键在于“找”到合适的直角三角形.
勾股定理的应用
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
解决
1.
