2021-2022学年人教版九年级上 24.2点和圆、直线和圆的位置关系同步练习
文档属性
| 名称 | 2021-2022学年人教版九年级上 24.2点和圆、直线和圆的位置关系同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版九年级上 24.2点和圆、直线和圆的位置关系同步练习
一.选择题
1.(2021秋 龙湾区期中)已知⊙O的半径为5,OA=6,则点A在( )
A.⊙O内 B.⊙O上 C.⊙O外 D.无法确定
2.(2021秋 莘县期中)已知半径为5的圆,直线l上一点到圆心的距离是5,则直线和圆的位置关系为( )
A.相切 B.相离 C.相切或相交 D.相切或相离
3.(2021秋 溧水区期中)已知⊙O的半径为4,直线l上有一点M.若OM=4,则直线l与⊙O的位置关系是( )
A.相交 B.相离或相交 C.相离或相切 D.相交或相切
4.(2021 安阳一模)如图,PA是⊙O的切线,A为切点,连接OP交⊙O于点C,点B在⊙O上,且∠ABC=24°,则∠APC等于( )
A.31° B.42° C.53° D.64°
5.(2021秋 沙坪坝区校级期中)如图,PA、PB分别与⊙O相切于A、B两点,C是圆上一点,连接AC、BC,若∠ACB=62°,则∠P的度数为( )
A.56° B.62° C.66° D.68°
6.(2020秋 北碚区校级期末)如图,⊙O是△ABC的外接圆,∠CAB=30°,∠ACB=105°,CD⊥AB于点D且CD=2,则⊙O的半径为( )
A.2 B.4 C.4 D.4
7.(2020秋 衢江区期末)如图,PA、PB分别切⊙O于点A、B,且PA=8,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长为( )
A.32 B.24 C.16 D.8
8.(2021 荆门一模)如图,点O为△ABC的内心,∠A=60°,OB=2,OC=4,则△OBC的面积是( )
A. B. C.2 D.4
9.(2021 安徽模拟)如图,O为Rt△ABC的内心,∠A=90°,AB=6,AC=8,OD∥AB交BC于点D,则CD的值为( )
A. B. C.8 D.
10.(2021秋 滨城区期中)已知PA,PB是⊙O的切线,A,B是切点,点C是⊙O上不同于点A、点B的一个动点,若∠P=54°,则∠ACB的度数是( )
A.63° B.117° C.53°或127° D.117°或63°
11.(2020 高青县一模)如图,以△ABC的一边AB为直径作⊙O,交于BC的中点D,过点D作直线EF与⊙O相切,交AC于点E,交AB的延长线于点F.若△ABC的面积为△CDE的面积的8倍,则下列结论中,错误的是( )
A.AC=2AO B.EF=2AE C.AB=2BF D.DF=2DE
12.(2021 鹿城区校级二模)如图,PA,PB是⊙O的切线,切点分别为A,B.BC是⊙O的直径,连结AC,若AC=1,BC=,则PA=( )
A. B.2 C. D.
二.填空题
13.(2021秋 西城区校级期中)已知∠AOB=30°,P是OA上的一点,OP=4cm,以r为半径作⊙P.若r=cm,则⊙P与OB的位置关系是 .
14.(2021秋 下城区校级期中)已知点P到圆上的点的最大距离为11,最小距离为7,则此圆的半径为 .
15.(2021秋 姜堰区期中)如图,I是△ABC的内心,∠A=50°,则∠BIC= .
16.(2021秋 亭湖区月考)矩形ABCD中,边AB=6cm,AD=8cm,以A为圆心作⊙A,使B、C、D三点有两个点在⊙A内,有一点在⊙A外,则⊙A的半径r的取值范围是 .
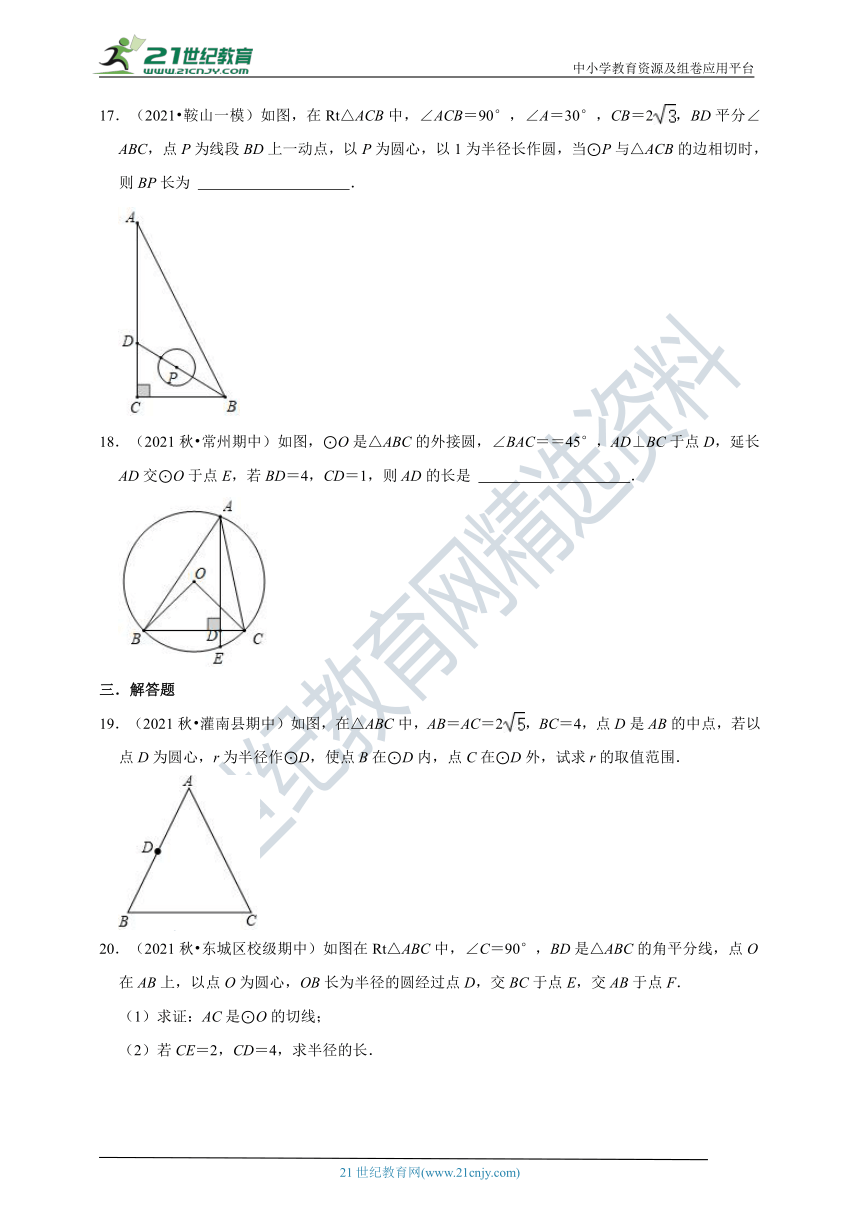
17.(2021 鞍山一模)如图,在Rt△ACB中,∠ACB=90°,∠A=30°,CB=2,BD平分∠ABC,点P为线段BD上一动点,以P为圆心,以1为半径长作圆,当⊙P与△ACB的边相切时,则BP长为 .
18.(2021秋 常州期中)如图,⊙O是△ABC的外接圆,∠BAC==45°,AD⊥BC于点D,延长AD交⊙O于点E,若BD=4,CD=1,则AD的长是 .
三.解答题
19.(2021秋 灌南县期中)如图,在△ABC中,AB=AC=2,BC=4,点D是AB的中点,若以点D为圆心,r为半径作⊙D,使点B在⊙D内,点C在⊙D外,试求r的取值范围.
20.(2021秋 东城区校级期中)如图在Rt△ABC中,∠C=90°,BD是△ABC的角平分线,点O在AB上,以点O为圆心,OB长为半径的圆经过点D,交BC于点E,交AB于点F.
(1)求证:AC是⊙O的切线;
(2)若CE=2,CD=4,求半径的长.
21.(2021 南浔区模拟)如图,AB为⊙O的直径,PQ是⊙O的切线,E为切点,AC⊥PQ于C,交⊙O于D.
(1)求证:AE平分∠BAC;
(2)若AD=EC=2,求⊙O的半径.
22.(2021 临海市一模)如图,⊙O是△ABC的外接圆,且AB=AC,四边形ABCD是平行四边形,边CD与⊙O交于点E,连接AE.
(1)求证:AE=AD;
(2)若∠B=72°,求证:点E是的中点.
23.(2020秋 宁蒗县期末)已知:在△ABC中,∠C=90°,⊙I是Rt△ABC的内切圆,切点分别为D、E、F,连接IE、IF.
(1)四边形IECF是什么特殊的四边形?并说明理由.
(2)若AC=8,BC=6,求半径IE的长.
24.(2021 江都区模拟)如图,AB是⊙O的直径,C是⊙O上一点,过点C作⊙O的切线,交BA的延长线交于点D,过点B作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC.
(1)求证:∠ECB=∠EBC;
(2)连接BF,CO,若BF=5,sin∠FBC=,求AC的长.
25.(2021 夹江县模拟)如图,AB是⊙O的直径,点C是⊙O上的一点,OD⊥AB交AC于点E,∠D=2∠A.
(1)求证:CD是⊙O的切线;
(2)求证:DE=DC;
(3)若OD=5,CD=3,求AE的长.
26.(2020秋 大冶市期末)如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D、过D作直线DG∥BC.
(1)求证:DG是⊙O的切线;
(2)求证:DE=CD;
(3)若DE=2,BC=8,求⊙O的半径.
答案与解析
一.选择题
1.(2021秋 龙湾区期中)已知⊙O的半径为5,OA=6,则点A在( )
A.⊙O内 B.⊙O上 C.⊙O外 D.无法确定
【解析】解:∵OA=6>5,
∴点A与⊙O的位置关系是点在圆外,
故选:C.
2.(2021秋 莘县期中)已知半径为5的圆,直线l上一点到圆心的距离是5,则直线和圆的位置关系为( )
A.相切 B.相离 C.相切或相交 D.相切或相离
【解析】解:∵若直线L与⊙O只有一个交点,即为点P,则直线L与⊙O的位置关系为:相切;
若直线L与⊙O有两个交点,其中一个为点P,则直线L与⊙O的位置关系为:相交;
∴直线L与⊙O的位置关系为:相交或相切.
故选:C.
3.(2021秋 溧水区期中)已知⊙O的半径为4,直线l上有一点M.若OM=4,则直线l与⊙O的位置关系是( )
A.相交 B.相离或相交 C.相离或相切 D.相交或相切
【解析】解:当OM垂直于直线l时,即圆心O到直线l的距离d=4=r,⊙O与l相切;
当OM不垂直于直线l时,即圆心O到直线l的距离d<4=r,⊙O与直线l相交.
故直线l与⊙O的位置关系是相切或相交.
故选:D.
4.(2021 安阳一模)如图,PA是⊙O的切线,A为切点,连接OP交⊙O于点C,点B在⊙O上,且∠ABC=24°,则∠APC等于( )
A.31° B.42° C.53° D.64°
【解析】解:连接OA,
∵∠ABC=24°,
∴∠AOC=2∠ABC=48°,
∵PA是⊙O的切线,
∴∠OAP=90°,
∴∠APC=90°﹣∠AOP=42°,
故选:B.
5.(2021秋 沙坪坝区校级期中)如图,PA、PB分别与⊙O相切于A、B两点,C是圆上一点,连接AC、BC,若∠ACB=62°,则∠P的度数为( )
A.56° B.62° C.66° D.68°
【解析】解:连接OA、OB,
由圆周角定理得:∠AOB=2∠ACB=124°,
∵PA、PB分别与⊙O相切于A、B两点,
∴∠OAP=∠OBP=90°,
∴∠P=360°﹣90°﹣90°﹣124°=56°,
故选:A.
6.(2020秋 北碚区校级期末)如图,⊙O是△ABC的外接圆,∠CAB=30°,∠ACB=105°,CD⊥AB于点D且CD=2,则⊙O的半径为( )
A.2 B.4 C.4 D.4
【解析】解:如图,连接OA,OC,
∵CD⊥AB,
∴∠ADC=90°,
∵∠CAB=30°,CD=2,
∴AC=2CD=4,
∵∠ACB=105°,∠ACD=60°,
∴∠CBA=45°,
∵∠COA=2∠CBA=2×45°=90°,
在Rt△AOC中,由勾股定理得:AC2=OA2+OC2,
∵OA=OC,
∴OA=AC=4,
∴⊙O的半径为4,
故选:B.
7.(2020秋 衢江区期末)如图,PA、PB分别切⊙O于点A、B,且PA=8,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长为( )
A.32 B.24 C.16 D.8
【解析】解:∵PA、PB分别切⊙O于点A、B,
∴PA=PB=8,
∵CD切⊙O于点E,
∴CA=CE,DB=DE,
∴△PCD的周长=PC+CD+PD=PC+CE+DE+PD=PC+AC+BD+PD=PA+PB=16.
故选:C.
8.(2021 荆门一模)如图,点O为△ABC的内心,∠A=60°,OB=2,OC=4,则△OBC的面积是( )
A. B. C.2 D.4
【解析】解:如图,过点C作CH⊥BO的延长线于点H,
∵点O为△ABC的内心,∠A=60°,
∴∠BOC=180°﹣∠OBC﹣∠OCB=90°+A=120°,
∴∠COH=60°,
∵OB=2,OC=4,
∴OH=2
∴CH=2,
∴△OBC的面积=OB CH=2×2=2.
故选:B.
9.(2021 安徽模拟)如图,O为Rt△ABC的内心,∠A=90°,AB=6,AC=8,OD∥AB交BC于点D,则CD的值为( )
A. B. C.8 D.
【解析】解:如图,设圆O与Rt△ABC分别切于点E、F、G,
设OE=OF=OG=x,
∵圆O与Rt△ABC分别切于点E、F、G,
∴OE⊥AC,OF⊥AB,OG⊥BC,
∴四边形OEAF为矩形,
∵OE=OF,
∴四边形OEAF为正方形,
∴AE=AF=OE=OF=x,
∵AB=6,AC=8,
∴BG=BF=6﹣x,CG=CE=8﹣x,
∵BC=,
∴6﹣x+8﹣x=10,
∴x=2,
∴CE=CA﹣AE=8﹣2=6,
∵OD∥AB,∠A=90°,OE⊥AC,
∴D、O、E三点共线,
∴OE∥AB,
∴,
∴,
∴CD=,
故选:A.
10.(2021秋 滨城区期中)已知PA,PB是⊙O的切线,A,B是切点,点C是⊙O上不同于点A、点B的一个动点,若∠P=54°,则∠ACB的度数是( )
A.63° B.117° C.53°或127° D.117°或63°
【解析】解:连接OA,OB,
∵PA、PB是⊙O的切线,
∴OA⊥AP,OB⊥PB,
∴∠OAP=∠OBP=90°,
∵∠APB=54°,
∴∠AOB=126°,
当C在优弧ACB上时,∠ACB=∠AOB=63°;
当C′在弧AB上时,∠AC′B=180°﹣∠ACB=117°,
则∠ACB的度数为63°或117°,
故选:D.
11.(2020 高青县一模)如图,以△ABC的一边AB为直径作⊙O,交于BC的中点D,过点D作直线EF与⊙O相切,交AC于点E,交AB的延长线于点F.若△ABC的面积为△CDE的面积的8倍,则下列结论中,错误的是( )
A.AC=2AO B.EF=2AE C.AB=2BF D.DF=2DE
【解析】解:连接OD、AD,
∵OB=OA,BD=DC,
∴AC=2OD,
∵OA=OD,
∴AC=2OD,A正确,不符合题意;
∵EF是⊙O的切线,
∴OD⊥EF,
∵OB=OA,BD=DC,
∴OD∥AC,
∴AE⊥EF,
∵△ABC的面积为△CDE的面积的8倍,D是BC的中点,
∴△ADC的面积为△CDE的面积的4倍,
∴△ADE的面积为△CDE的面积的3倍,
∴AE=3EC,
∴=,
∵OD∥AC,
∴==,
∴FA=2AE,B错误,符合题意;
AB=2BF,C正确,不符合题意;
==,
∴DF=2DE,D正确,不符合题意;
故选:B.
12.(2021 鹿城区校级二模)如图,PA,PB是⊙O的切线,切点分别为A,B.BC是⊙O的直径,连结AC,若AC=1,BC=,则PA=( )
A. B.2 C. D.
【解析】解:连接OP,
∵BC是⊙O的直径,
∴∠CAB=90°,
∵AC=1,BC=,
∴AB==2,
∵PA、PB是⊙O的切线,
∴CB⊥PB,PA=PB,
∴∠POB=∠ACB,
∴tan∠POB=tan∠ACB=2,
∴=2,即=2,
解得:PB=,
∴PA=,
故选:C.
二.填空题
13.(2021秋 西城区校级期中)已知∠AOB=30°,P是OA上的一点,OP=4cm,以r为半径作⊙P.若r=cm,则⊙P与OB的位置关系是 相离 .
【解析】解:过点P作PC⊥OB,垂足为D,则∠OCP=90°,
∵∠AOB=30°,OP=4cm,
∴PC=OP=2cm.
当r=cm时,r<PD,
∴⊙P与OB相离,
即⊙P与OB位置关系是相离.
故答案为:相离.
14.(2021秋 下城区校级期中)已知点P到圆上的点的最大距离为11,最小距离为7,则此圆的半径为 2或9 .
【解析】解:如图,分为两种情况:
①当点P在圆内时,最近点的距离为7,最大距离为11,则直径是18,因而半径是9;
②当点P在圆外时,最近点的距离为7,最大距离为11,则直径是4,因而半径是2.
故此圆的半径为2或9,
故答案为:2或9.
15.(2021秋 姜堰区期中)如图,I是△ABC的内心,∠A=50°,则∠BIC= 115° .
【解析】解:∵∠A=50°,
∴∠ABC+∠ACB=130°,
∵△ABC的内心为I,
∴BI和CI分别平分∠ABC和∠ACB,
∴∠IBC=ABC,∠ICB=ACB,
∴∠BIC=180°﹣(∠IBC+∠ICB)
=180°﹣(∠ABC+∠ACB)
=180°﹣×130°
=115°,
故答案为:115°.
16.(2021秋 亭湖区月考)矩形ABCD中,边AB=6cm,AD=8cm,以A为圆心作⊙A,使B、C、D三点有两个点在⊙A内,有一点在⊙A外,则⊙A的半径r的取值范围是 8(cm)<r<10(cm) .
【解析】解:连接AC,
∵矩形ABCD,
∴AB=CD=6(cm),∠ADC=90°,
在Rt△ACD中,
AC==10(cm),
当点D在⊙A上时,半径r=8cm,
当点C在⊙A上时,半径r=10cm,
∴当点B、C、D三点有两个点在⊙A内,有一点在⊙A外需满足8(cm)<r<10(cm),
故答案为8(cm)<r<10(cm).
17.(2021 鞍山一模)如图,在Rt△ACB中,∠ACB=90°,∠A=30°,CB=2,BD平分∠ABC,点P为线段BD上一动点,以P为圆心,以1为半径长作圆,当⊙P与△ACB的边相切时,则BP长为 2或 .
【解析】解:∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=30°,
∵BC=2,
∴DC=,
∴BD=2DC=4,
①若⊙P与BC相切于点E,连接PE,则∠PEB=90°,
∵PE=1,∠PBE=30°,
∴PB=2,
∵BD平分∠ABC,
过点P作PF⊥AB,
∴PE=PF,
∴此时⊙P与AB相切;
②若⊙P与AC相切于点E,连接PE,则PE⊥AC,
∴PE∥BC,
∴∠DPE=30°,
∵PE=1,
∴DE=,
∴PD=2DE=,
∴PB=BD﹣PD=4﹣,
综合以上可得,当⊙P与△ACB的边相切时,BP长为2或4﹣.
故答案为2或.
18.(2021秋 常州期中)如图,⊙O是△ABC的外接圆,∠BAC==45°,AD⊥BC于点D,延长AD交⊙O于点E,若BD=4,CD=1,则AD的长是 .
【解析】解:如图,连接OA,过O点作OF⊥BC于F,作OG⊥AE于G,
∵⊙O是△ABC的外接圆,∠BAC=45°,
∴∠BOC=90°,
∵BD=4,CD=1,
∴BC=4+1=5,
∴OB=OC=,
∴OA=,OF=BF=,
∴DF=BD﹣BF=,
∴OG=,GD=,
在Rt△AGO中,AG==,
∴AD=AG+GD=.
故答案为:.
三.解答题
19.(2021秋 灌南县期中)如图,在△ABC中,AB=AC=2,BC=4,点D是AB的中点,若以点D为圆心,r为半径作⊙D,使点B在⊙D内,点C在⊙D外,试求r的取值范围.
【解析】解:连接CD,,过点A作AE⊥BC于点E.过点D作DF⊥BC于点F,显然DF∥AE,
∵AB=AC=2,BC=4,
∴BE=BC=2,
∴AE==4,,
∵点D是AB中点,即DF是中位线
∴DF=AE=2,BF=BE=1,
∴CF=3,
∴CD==,
又DB=AB=,
∴r的取值范围是<r<.
20.(2021秋 东城区校级期中)如图在Rt△ABC中,∠C=90°,BD是△ABC的角平分线,点O在AB上,以点O为圆心,OB长为半径的圆经过点D,交BC于点E,交AB于点F.
(1)求证:AC是⊙O的切线;
(2)若CE=2,CD=4,求半径的长.
【解析】(1)证明:如图,连接OD,
∵OD=OB,
∴∠ODB=∠OBD,
∵BD是△ABC的角平分线,
∴∠OBD=∠DBC,
∴∠ODB=∠DBC,
∴OD∥BC,
∴∠ODA=∠C=90°,
∵AC经过⊙为的半径OD的端点D,且AC⊥OD,
∴AC是⊙O的切线.
(2)如图,设⊙O的半径为r,则OB=OG=r,
作OG⊥BE于点G,则BG=EG,∠OGB=90°,
∵∠ODC=∠C=∠OGC=90°,
∴四边形ODCG是矩形,
∵CE=2,CD=4,
∴OG=CD=4,CG=OD=r,
∴BG=EG=r﹣2,
∵OB2=OG2+BG2,
∴r2=42+(r﹣2)2,
解得r=5,
∴⊙O的半径长为5.
21.(2021 南浔区模拟)如图,AB为⊙O的直径,PQ是⊙O的切线,E为切点,AC⊥PQ于C,交⊙O于D.
(1)求证:AE平分∠BAC;
(2)若AD=EC=2,求⊙O的半径.
【解析】(1)证明:连接OE,
∴OA=OE,
∴∠OEA=∠OAE,
∵PQ切⊙O于E,
∴OE⊥PQ,
∵AC⊥PQ,
∴OE∥AC,
∴∠OEA=∠EAC,
∴∠OAE=∠EAC,
∴AE平分∠BAC;
(2)解:过点O作OM⊥AC于M,
∴AM=MD=AD,
∵AD=EC=2,
∴AM=MD=1,
又∠OEC=∠ACE=∠OMC=90°,
∴四边形OECM为矩形,
∴OM=EC=2,
在Rt△AOM中,OA===,
即⊙O的半径为.
22.(2021 临海市一模)如图,⊙O是△ABC的外接圆,且AB=AC,四边形ABCD是平行四边形,边CD与⊙O交于点E,连接AE.
(1)求证:AE=AD;
(2)若∠B=72°,求证:点E是的中点.
【解析】证明:(1)∵四边形ABCD是平行四边形,
∴∠ABC=∠D,
∵四边形ABCE为⊙O的内接四边形,
∴∠ABC+∠AEC=180°,
∵∠AED+∠AEC=180°,
∴∠ABC=∠AED,
∴∠D=∠AED,
∴AE=AD;
(2)∵AB=AC,∠B=72°,
∴∠ABC=∠ACB=72°,∠AEC=180°﹣∠B=108°,
∴∠BAC=180°﹣72°×2=36°,
∵AB∥CD,
∴∠ACE=∠BAC=36°,
∴∠EAC=180°﹣∠AEC﹣∠ACE=36°,
∴∠ACE=∠EAC,
∴=,即点E是的中点.
23.(2020秋 宁蒗县期末)已知:在△ABC中,∠C=90°,⊙I是Rt△ABC的内切圆,切点分别为D、E、F,连接IE、IF.
(1)四边形IECF是什么特殊的四边形?并说明理由.
(2)若AC=8,BC=6,求半径IE的长.
【解析】解:(1)四边形IECF是正方形,理由如下:
∵⊙I是Rt△ABC的内切圆,即AC、BC都是⊙I的切线,
∴∠IEC=∠IFC=90°,
∵∠C=90°,
∴四边形IECF是矩形,
∵IE=IF,
∴四边形IECF是正方形;
(2)在△ABC中,∠C=90°,AC=8,BC=6,
∴AB===10,
由切线长定理可知:
AE=AD,BD=BF,CE=CF,
设半径IE的长为x,则CE=CF=x,
∴AE=AD=8﹣x,BD=BF=6﹣x,
∴(8﹣x)+(6﹣x)=10,
解得x=2,
∴IE的长为2.
24.(2021 江都区模拟)如图,AB是⊙O的直径,C是⊙O上一点,过点C作⊙O的切线,交BA的延长线交于点D,过点B作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC.
(1)求证:∠ECB=∠EBC;
(2)连接BF,CO,若BF=5,sin∠FBC=,求AC的长.
【解析】解:(1)证明:∵BE⊥BA于点,
∴BE是⊙O的切线,而又已知EC是⊙O的切线,C为切点,
∴EC=EB,
∴∠ECB=∠EBC;
(2)如图所示,连接BF、CO,
∵EC=EB,OC=OB,
∴EO⊥BC,
∴∠CHF=∠CHO=90°,CH=BH,
∵在Rt△BFH中,BF=5,sin∠FBC=,
∴FH=BF sin∠FBC=5×=3,
∴由勾股定理得:BH=4,
设OB=OF=x,在Rt△BOH中,由勾股定理得:
x2=42+(x﹣3)2,
∴x=,
∴OH=,
∵O为AB中点,H为BC中点,
∴AC=2OH=.
∴AC的长为.
25.(2021 夹江县模拟)如图,AB是⊙O的直径,点C是⊙O上的一点,OD⊥AB交AC于点E,∠D=2∠A.
(1)求证:CD是⊙O的切线;
(2)求证:DE=DC;
(3)若OD=5,CD=3,求AE的长.
【解析】(1)证明:连接OC,如图,
∵OA=OC,
∴∠ACO=∠A,
∴∠COB=∠A+∠ACO=2∠A,
又∵∠D=2∠A,
∴∠D=∠COB.
又∵OD⊥AB,
∴∠COB+∠COD=90°,
∴∠D+∠COD=90°,即∠DCO=90°,
∴OC⊥DC,
又点C在⊙O上,
∴CD是⊙O的切线;
(2)证明:∵∠DCO=90°,
∴∠DCE+∠ACO=90°,
又∵OD⊥AB,
∴∠AEO+∠A=90°,
又∵∠A=∠ACO,∠DEC=∠AEO,
∴∠DEC=∠DCE,
∴DE=DC;
(3)解:∵∠DCO=90°,OD=5,DC=3,
∴OC===4,
∴OA=OC=4,
又DE=DC=3,
∴OE=OD﹣DE=2,
在Rt△AEO中,由勾股定理得:AE2=OA2+OE2=42+22=20,
∴AE=2.
26.(2020秋 大冶市期末)如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D、过D作直线DG∥BC.
(1)求证:DG是⊙O的切线;
(2)求证:DE=CD;
(3)若DE=2,BC=8,求⊙O的半径.
【解析】(1)证明:连接OD交BC于H,如图,
∵点E是△ABC的内心
∴AD平分∠BAC,
即∠BAD=∠CAD,
∴,
∴OD⊥BC,BH=CH,
∵DG∥BC,
∴OD⊥DG,
∴DG是⊙O的切线;
(2)证明:连接BD,
∵点E是△ABC的内心,
∴∠ABE=∠CBE,
∵∠DBC=∠BAD,
∴∠DEB=∠BAD+∠ABE=∠DBC+∠CBE=∠DBE,
即∠BED=∠DBE,
∴BD=DE,
∵,
∴BD=CD,
∴DE=CD;
(3)解:连接OD,OB,如图,
由(1)得OD⊥BC,BH=CH,
∵BC=8,
∴BH=CH=4,
∵DE=2,BD=DE,
∴BD=2,
在Rt△BHD中,BD2=BH2+HD2,
∴(2)2=42+HD2,解得:HD=2,
在Rt△BHO中,
r2=BH2+(r﹣2)2,解得:r=5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级上 24.2点和圆、直线和圆的位置关系同步练习
一.选择题
1.(2021秋 龙湾区期中)已知⊙O的半径为5,OA=6,则点A在( )
A.⊙O内 B.⊙O上 C.⊙O外 D.无法确定
2.(2021秋 莘县期中)已知半径为5的圆,直线l上一点到圆心的距离是5,则直线和圆的位置关系为( )
A.相切 B.相离 C.相切或相交 D.相切或相离
3.(2021秋 溧水区期中)已知⊙O的半径为4,直线l上有一点M.若OM=4,则直线l与⊙O的位置关系是( )
A.相交 B.相离或相交 C.相离或相切 D.相交或相切
4.(2021 安阳一模)如图,PA是⊙O的切线,A为切点,连接OP交⊙O于点C,点B在⊙O上,且∠ABC=24°,则∠APC等于( )
A.31° B.42° C.53° D.64°
5.(2021秋 沙坪坝区校级期中)如图,PA、PB分别与⊙O相切于A、B两点,C是圆上一点,连接AC、BC,若∠ACB=62°,则∠P的度数为( )
A.56° B.62° C.66° D.68°
6.(2020秋 北碚区校级期末)如图,⊙O是△ABC的外接圆,∠CAB=30°,∠ACB=105°,CD⊥AB于点D且CD=2,则⊙O的半径为( )
A.2 B.4 C.4 D.4
7.(2020秋 衢江区期末)如图,PA、PB分别切⊙O于点A、B,且PA=8,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长为( )
A.32 B.24 C.16 D.8
8.(2021 荆门一模)如图,点O为△ABC的内心,∠A=60°,OB=2,OC=4,则△OBC的面积是( )
A. B. C.2 D.4
9.(2021 安徽模拟)如图,O为Rt△ABC的内心,∠A=90°,AB=6,AC=8,OD∥AB交BC于点D,则CD的值为( )
A. B. C.8 D.
10.(2021秋 滨城区期中)已知PA,PB是⊙O的切线,A,B是切点,点C是⊙O上不同于点A、点B的一个动点,若∠P=54°,则∠ACB的度数是( )
A.63° B.117° C.53°或127° D.117°或63°
11.(2020 高青县一模)如图,以△ABC的一边AB为直径作⊙O,交于BC的中点D,过点D作直线EF与⊙O相切,交AC于点E,交AB的延长线于点F.若△ABC的面积为△CDE的面积的8倍,则下列结论中,错误的是( )
A.AC=2AO B.EF=2AE C.AB=2BF D.DF=2DE
12.(2021 鹿城区校级二模)如图,PA,PB是⊙O的切线,切点分别为A,B.BC是⊙O的直径,连结AC,若AC=1,BC=,则PA=( )
A. B.2 C. D.
二.填空题
13.(2021秋 西城区校级期中)已知∠AOB=30°,P是OA上的一点,OP=4cm,以r为半径作⊙P.若r=cm,则⊙P与OB的位置关系是 .
14.(2021秋 下城区校级期中)已知点P到圆上的点的最大距离为11,最小距离为7,则此圆的半径为 .
15.(2021秋 姜堰区期中)如图,I是△ABC的内心,∠A=50°,则∠BIC= .
16.(2021秋 亭湖区月考)矩形ABCD中,边AB=6cm,AD=8cm,以A为圆心作⊙A,使B、C、D三点有两个点在⊙A内,有一点在⊙A外,则⊙A的半径r的取值范围是 .
17.(2021 鞍山一模)如图,在Rt△ACB中,∠ACB=90°,∠A=30°,CB=2,BD平分∠ABC,点P为线段BD上一动点,以P为圆心,以1为半径长作圆,当⊙P与△ACB的边相切时,则BP长为 .
18.(2021秋 常州期中)如图,⊙O是△ABC的外接圆,∠BAC==45°,AD⊥BC于点D,延长AD交⊙O于点E,若BD=4,CD=1,则AD的长是 .
三.解答题
19.(2021秋 灌南县期中)如图,在△ABC中,AB=AC=2,BC=4,点D是AB的中点,若以点D为圆心,r为半径作⊙D,使点B在⊙D内,点C在⊙D外,试求r的取值范围.
20.(2021秋 东城区校级期中)如图在Rt△ABC中,∠C=90°,BD是△ABC的角平分线,点O在AB上,以点O为圆心,OB长为半径的圆经过点D,交BC于点E,交AB于点F.
(1)求证:AC是⊙O的切线;
(2)若CE=2,CD=4,求半径的长.
21.(2021 南浔区模拟)如图,AB为⊙O的直径,PQ是⊙O的切线,E为切点,AC⊥PQ于C,交⊙O于D.
(1)求证:AE平分∠BAC;
(2)若AD=EC=2,求⊙O的半径.
22.(2021 临海市一模)如图,⊙O是△ABC的外接圆,且AB=AC,四边形ABCD是平行四边形,边CD与⊙O交于点E,连接AE.
(1)求证:AE=AD;
(2)若∠B=72°,求证:点E是的中点.
23.(2020秋 宁蒗县期末)已知:在△ABC中,∠C=90°,⊙I是Rt△ABC的内切圆,切点分别为D、E、F,连接IE、IF.
(1)四边形IECF是什么特殊的四边形?并说明理由.
(2)若AC=8,BC=6,求半径IE的长.
24.(2021 江都区模拟)如图,AB是⊙O的直径,C是⊙O上一点,过点C作⊙O的切线,交BA的延长线交于点D,过点B作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC.
(1)求证:∠ECB=∠EBC;
(2)连接BF,CO,若BF=5,sin∠FBC=,求AC的长.
25.(2021 夹江县模拟)如图,AB是⊙O的直径,点C是⊙O上的一点,OD⊥AB交AC于点E,∠D=2∠A.
(1)求证:CD是⊙O的切线;
(2)求证:DE=DC;
(3)若OD=5,CD=3,求AE的长.
26.(2020秋 大冶市期末)如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D、过D作直线DG∥BC.
(1)求证:DG是⊙O的切线;
(2)求证:DE=CD;
(3)若DE=2,BC=8,求⊙O的半径.
答案与解析
一.选择题
1.(2021秋 龙湾区期中)已知⊙O的半径为5,OA=6,则点A在( )
A.⊙O内 B.⊙O上 C.⊙O外 D.无法确定
【解析】解:∵OA=6>5,
∴点A与⊙O的位置关系是点在圆外,
故选:C.
2.(2021秋 莘县期中)已知半径为5的圆,直线l上一点到圆心的距离是5,则直线和圆的位置关系为( )
A.相切 B.相离 C.相切或相交 D.相切或相离
【解析】解:∵若直线L与⊙O只有一个交点,即为点P,则直线L与⊙O的位置关系为:相切;
若直线L与⊙O有两个交点,其中一个为点P,则直线L与⊙O的位置关系为:相交;
∴直线L与⊙O的位置关系为:相交或相切.
故选:C.
3.(2021秋 溧水区期中)已知⊙O的半径为4,直线l上有一点M.若OM=4,则直线l与⊙O的位置关系是( )
A.相交 B.相离或相交 C.相离或相切 D.相交或相切
【解析】解:当OM垂直于直线l时,即圆心O到直线l的距离d=4=r,⊙O与l相切;
当OM不垂直于直线l时,即圆心O到直线l的距离d<4=r,⊙O与直线l相交.
故直线l与⊙O的位置关系是相切或相交.
故选:D.
4.(2021 安阳一模)如图,PA是⊙O的切线,A为切点,连接OP交⊙O于点C,点B在⊙O上,且∠ABC=24°,则∠APC等于( )
A.31° B.42° C.53° D.64°
【解析】解:连接OA,
∵∠ABC=24°,
∴∠AOC=2∠ABC=48°,
∵PA是⊙O的切线,
∴∠OAP=90°,
∴∠APC=90°﹣∠AOP=42°,
故选:B.
5.(2021秋 沙坪坝区校级期中)如图,PA、PB分别与⊙O相切于A、B两点,C是圆上一点,连接AC、BC,若∠ACB=62°,则∠P的度数为( )
A.56° B.62° C.66° D.68°
【解析】解:连接OA、OB,
由圆周角定理得:∠AOB=2∠ACB=124°,
∵PA、PB分别与⊙O相切于A、B两点,
∴∠OAP=∠OBP=90°,
∴∠P=360°﹣90°﹣90°﹣124°=56°,
故选:A.
6.(2020秋 北碚区校级期末)如图,⊙O是△ABC的外接圆,∠CAB=30°,∠ACB=105°,CD⊥AB于点D且CD=2,则⊙O的半径为( )
A.2 B.4 C.4 D.4
【解析】解:如图,连接OA,OC,
∵CD⊥AB,
∴∠ADC=90°,
∵∠CAB=30°,CD=2,
∴AC=2CD=4,
∵∠ACB=105°,∠ACD=60°,
∴∠CBA=45°,
∵∠COA=2∠CBA=2×45°=90°,
在Rt△AOC中,由勾股定理得:AC2=OA2+OC2,
∵OA=OC,
∴OA=AC=4,
∴⊙O的半径为4,
故选:B.
7.(2020秋 衢江区期末)如图,PA、PB分别切⊙O于点A、B,且PA=8,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长为( )
A.32 B.24 C.16 D.8
【解析】解:∵PA、PB分别切⊙O于点A、B,
∴PA=PB=8,
∵CD切⊙O于点E,
∴CA=CE,DB=DE,
∴△PCD的周长=PC+CD+PD=PC+CE+DE+PD=PC+AC+BD+PD=PA+PB=16.
故选:C.
8.(2021 荆门一模)如图,点O为△ABC的内心,∠A=60°,OB=2,OC=4,则△OBC的面积是( )
A. B. C.2 D.4
【解析】解:如图,过点C作CH⊥BO的延长线于点H,
∵点O为△ABC的内心,∠A=60°,
∴∠BOC=180°﹣∠OBC﹣∠OCB=90°+A=120°,
∴∠COH=60°,
∵OB=2,OC=4,
∴OH=2
∴CH=2,
∴△OBC的面积=OB CH=2×2=2.
故选:B.
9.(2021 安徽模拟)如图,O为Rt△ABC的内心,∠A=90°,AB=6,AC=8,OD∥AB交BC于点D,则CD的值为( )
A. B. C.8 D.
【解析】解:如图,设圆O与Rt△ABC分别切于点E、F、G,
设OE=OF=OG=x,
∵圆O与Rt△ABC分别切于点E、F、G,
∴OE⊥AC,OF⊥AB,OG⊥BC,
∴四边形OEAF为矩形,
∵OE=OF,
∴四边形OEAF为正方形,
∴AE=AF=OE=OF=x,
∵AB=6,AC=8,
∴BG=BF=6﹣x,CG=CE=8﹣x,
∵BC=,
∴6﹣x+8﹣x=10,
∴x=2,
∴CE=CA﹣AE=8﹣2=6,
∵OD∥AB,∠A=90°,OE⊥AC,
∴D、O、E三点共线,
∴OE∥AB,
∴,
∴,
∴CD=,
故选:A.
10.(2021秋 滨城区期中)已知PA,PB是⊙O的切线,A,B是切点,点C是⊙O上不同于点A、点B的一个动点,若∠P=54°,则∠ACB的度数是( )
A.63° B.117° C.53°或127° D.117°或63°
【解析】解:连接OA,OB,
∵PA、PB是⊙O的切线,
∴OA⊥AP,OB⊥PB,
∴∠OAP=∠OBP=90°,
∵∠APB=54°,
∴∠AOB=126°,
当C在优弧ACB上时,∠ACB=∠AOB=63°;
当C′在弧AB上时,∠AC′B=180°﹣∠ACB=117°,
则∠ACB的度数为63°或117°,
故选:D.
11.(2020 高青县一模)如图,以△ABC的一边AB为直径作⊙O,交于BC的中点D,过点D作直线EF与⊙O相切,交AC于点E,交AB的延长线于点F.若△ABC的面积为△CDE的面积的8倍,则下列结论中,错误的是( )
A.AC=2AO B.EF=2AE C.AB=2BF D.DF=2DE
【解析】解:连接OD、AD,
∵OB=OA,BD=DC,
∴AC=2OD,
∵OA=OD,
∴AC=2OD,A正确,不符合题意;
∵EF是⊙O的切线,
∴OD⊥EF,
∵OB=OA,BD=DC,
∴OD∥AC,
∴AE⊥EF,
∵△ABC的面积为△CDE的面积的8倍,D是BC的中点,
∴△ADC的面积为△CDE的面积的4倍,
∴△ADE的面积为△CDE的面积的3倍,
∴AE=3EC,
∴=,
∵OD∥AC,
∴==,
∴FA=2AE,B错误,符合题意;
AB=2BF,C正确,不符合题意;
==,
∴DF=2DE,D正确,不符合题意;
故选:B.
12.(2021 鹿城区校级二模)如图,PA,PB是⊙O的切线,切点分别为A,B.BC是⊙O的直径,连结AC,若AC=1,BC=,则PA=( )
A. B.2 C. D.
【解析】解:连接OP,
∵BC是⊙O的直径,
∴∠CAB=90°,
∵AC=1,BC=,
∴AB==2,
∵PA、PB是⊙O的切线,
∴CB⊥PB,PA=PB,
∴∠POB=∠ACB,
∴tan∠POB=tan∠ACB=2,
∴=2,即=2,
解得:PB=,
∴PA=,
故选:C.
二.填空题
13.(2021秋 西城区校级期中)已知∠AOB=30°,P是OA上的一点,OP=4cm,以r为半径作⊙P.若r=cm,则⊙P与OB的位置关系是 相离 .
【解析】解:过点P作PC⊥OB,垂足为D,则∠OCP=90°,
∵∠AOB=30°,OP=4cm,
∴PC=OP=2cm.
当r=cm时,r<PD,
∴⊙P与OB相离,
即⊙P与OB位置关系是相离.
故答案为:相离.
14.(2021秋 下城区校级期中)已知点P到圆上的点的最大距离为11,最小距离为7,则此圆的半径为 2或9 .
【解析】解:如图,分为两种情况:
①当点P在圆内时,最近点的距离为7,最大距离为11,则直径是18,因而半径是9;
②当点P在圆外时,最近点的距离为7,最大距离为11,则直径是4,因而半径是2.
故此圆的半径为2或9,
故答案为:2或9.
15.(2021秋 姜堰区期中)如图,I是△ABC的内心,∠A=50°,则∠BIC= 115° .
【解析】解:∵∠A=50°,
∴∠ABC+∠ACB=130°,
∵△ABC的内心为I,
∴BI和CI分别平分∠ABC和∠ACB,
∴∠IBC=ABC,∠ICB=ACB,
∴∠BIC=180°﹣(∠IBC+∠ICB)
=180°﹣(∠ABC+∠ACB)
=180°﹣×130°
=115°,
故答案为:115°.
16.(2021秋 亭湖区月考)矩形ABCD中,边AB=6cm,AD=8cm,以A为圆心作⊙A,使B、C、D三点有两个点在⊙A内,有一点在⊙A外,则⊙A的半径r的取值范围是 8(cm)<r<10(cm) .
【解析】解:连接AC,
∵矩形ABCD,
∴AB=CD=6(cm),∠ADC=90°,
在Rt△ACD中,
AC==10(cm),
当点D在⊙A上时,半径r=8cm,
当点C在⊙A上时,半径r=10cm,
∴当点B、C、D三点有两个点在⊙A内,有一点在⊙A外需满足8(cm)<r<10(cm),
故答案为8(cm)<r<10(cm).
17.(2021 鞍山一模)如图,在Rt△ACB中,∠ACB=90°,∠A=30°,CB=2,BD平分∠ABC,点P为线段BD上一动点,以P为圆心,以1为半径长作圆,当⊙P与△ACB的边相切时,则BP长为 2或 .
【解析】解:∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=30°,
∵BC=2,
∴DC=,
∴BD=2DC=4,
①若⊙P与BC相切于点E,连接PE,则∠PEB=90°,
∵PE=1,∠PBE=30°,
∴PB=2,
∵BD平分∠ABC,
过点P作PF⊥AB,
∴PE=PF,
∴此时⊙P与AB相切;
②若⊙P与AC相切于点E,连接PE,则PE⊥AC,
∴PE∥BC,
∴∠DPE=30°,
∵PE=1,
∴DE=,
∴PD=2DE=,
∴PB=BD﹣PD=4﹣,
综合以上可得,当⊙P与△ACB的边相切时,BP长为2或4﹣.
故答案为2或.
18.(2021秋 常州期中)如图,⊙O是△ABC的外接圆,∠BAC==45°,AD⊥BC于点D,延长AD交⊙O于点E,若BD=4,CD=1,则AD的长是 .
【解析】解:如图,连接OA,过O点作OF⊥BC于F,作OG⊥AE于G,
∵⊙O是△ABC的外接圆,∠BAC=45°,
∴∠BOC=90°,
∵BD=4,CD=1,
∴BC=4+1=5,
∴OB=OC=,
∴OA=,OF=BF=,
∴DF=BD﹣BF=,
∴OG=,GD=,
在Rt△AGO中,AG==,
∴AD=AG+GD=.
故答案为:.
三.解答题
19.(2021秋 灌南县期中)如图,在△ABC中,AB=AC=2,BC=4,点D是AB的中点,若以点D为圆心,r为半径作⊙D,使点B在⊙D内,点C在⊙D外,试求r的取值范围.
【解析】解:连接CD,,过点A作AE⊥BC于点E.过点D作DF⊥BC于点F,显然DF∥AE,
∵AB=AC=2,BC=4,
∴BE=BC=2,
∴AE==4,,
∵点D是AB中点,即DF是中位线
∴DF=AE=2,BF=BE=1,
∴CF=3,
∴CD==,
又DB=AB=,
∴r的取值范围是<r<.
20.(2021秋 东城区校级期中)如图在Rt△ABC中,∠C=90°,BD是△ABC的角平分线,点O在AB上,以点O为圆心,OB长为半径的圆经过点D,交BC于点E,交AB于点F.
(1)求证:AC是⊙O的切线;
(2)若CE=2,CD=4,求半径的长.
【解析】(1)证明:如图,连接OD,
∵OD=OB,
∴∠ODB=∠OBD,
∵BD是△ABC的角平分线,
∴∠OBD=∠DBC,
∴∠ODB=∠DBC,
∴OD∥BC,
∴∠ODA=∠C=90°,
∵AC经过⊙为的半径OD的端点D,且AC⊥OD,
∴AC是⊙O的切线.
(2)如图,设⊙O的半径为r,则OB=OG=r,
作OG⊥BE于点G,则BG=EG,∠OGB=90°,
∵∠ODC=∠C=∠OGC=90°,
∴四边形ODCG是矩形,
∵CE=2,CD=4,
∴OG=CD=4,CG=OD=r,
∴BG=EG=r﹣2,
∵OB2=OG2+BG2,
∴r2=42+(r﹣2)2,
解得r=5,
∴⊙O的半径长为5.
21.(2021 南浔区模拟)如图,AB为⊙O的直径,PQ是⊙O的切线,E为切点,AC⊥PQ于C,交⊙O于D.
(1)求证:AE平分∠BAC;
(2)若AD=EC=2,求⊙O的半径.
【解析】(1)证明:连接OE,
∴OA=OE,
∴∠OEA=∠OAE,
∵PQ切⊙O于E,
∴OE⊥PQ,
∵AC⊥PQ,
∴OE∥AC,
∴∠OEA=∠EAC,
∴∠OAE=∠EAC,
∴AE平分∠BAC;
(2)解:过点O作OM⊥AC于M,
∴AM=MD=AD,
∵AD=EC=2,
∴AM=MD=1,
又∠OEC=∠ACE=∠OMC=90°,
∴四边形OECM为矩形,
∴OM=EC=2,
在Rt△AOM中,OA===,
即⊙O的半径为.
22.(2021 临海市一模)如图,⊙O是△ABC的外接圆,且AB=AC,四边形ABCD是平行四边形,边CD与⊙O交于点E,连接AE.
(1)求证:AE=AD;
(2)若∠B=72°,求证:点E是的中点.
【解析】证明:(1)∵四边形ABCD是平行四边形,
∴∠ABC=∠D,
∵四边形ABCE为⊙O的内接四边形,
∴∠ABC+∠AEC=180°,
∵∠AED+∠AEC=180°,
∴∠ABC=∠AED,
∴∠D=∠AED,
∴AE=AD;
(2)∵AB=AC,∠B=72°,
∴∠ABC=∠ACB=72°,∠AEC=180°﹣∠B=108°,
∴∠BAC=180°﹣72°×2=36°,
∵AB∥CD,
∴∠ACE=∠BAC=36°,
∴∠EAC=180°﹣∠AEC﹣∠ACE=36°,
∴∠ACE=∠EAC,
∴=,即点E是的中点.
23.(2020秋 宁蒗县期末)已知:在△ABC中,∠C=90°,⊙I是Rt△ABC的内切圆,切点分别为D、E、F,连接IE、IF.
(1)四边形IECF是什么特殊的四边形?并说明理由.
(2)若AC=8,BC=6,求半径IE的长.
【解析】解:(1)四边形IECF是正方形,理由如下:
∵⊙I是Rt△ABC的内切圆,即AC、BC都是⊙I的切线,
∴∠IEC=∠IFC=90°,
∵∠C=90°,
∴四边形IECF是矩形,
∵IE=IF,
∴四边形IECF是正方形;
(2)在△ABC中,∠C=90°,AC=8,BC=6,
∴AB===10,
由切线长定理可知:
AE=AD,BD=BF,CE=CF,
设半径IE的长为x,则CE=CF=x,
∴AE=AD=8﹣x,BD=BF=6﹣x,
∴(8﹣x)+(6﹣x)=10,
解得x=2,
∴IE的长为2.
24.(2021 江都区模拟)如图,AB是⊙O的直径,C是⊙O上一点,过点C作⊙O的切线,交BA的延长线交于点D,过点B作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC.
(1)求证:∠ECB=∠EBC;
(2)连接BF,CO,若BF=5,sin∠FBC=,求AC的长.
【解析】解:(1)证明:∵BE⊥BA于点,
∴BE是⊙O的切线,而又已知EC是⊙O的切线,C为切点,
∴EC=EB,
∴∠ECB=∠EBC;
(2)如图所示,连接BF、CO,
∵EC=EB,OC=OB,
∴EO⊥BC,
∴∠CHF=∠CHO=90°,CH=BH,
∵在Rt△BFH中,BF=5,sin∠FBC=,
∴FH=BF sin∠FBC=5×=3,
∴由勾股定理得:BH=4,
设OB=OF=x,在Rt△BOH中,由勾股定理得:
x2=42+(x﹣3)2,
∴x=,
∴OH=,
∵O为AB中点,H为BC中点,
∴AC=2OH=.
∴AC的长为.
25.(2021 夹江县模拟)如图,AB是⊙O的直径,点C是⊙O上的一点,OD⊥AB交AC于点E,∠D=2∠A.
(1)求证:CD是⊙O的切线;
(2)求证:DE=DC;
(3)若OD=5,CD=3,求AE的长.
【解析】(1)证明:连接OC,如图,
∵OA=OC,
∴∠ACO=∠A,
∴∠COB=∠A+∠ACO=2∠A,
又∵∠D=2∠A,
∴∠D=∠COB.
又∵OD⊥AB,
∴∠COB+∠COD=90°,
∴∠D+∠COD=90°,即∠DCO=90°,
∴OC⊥DC,
又点C在⊙O上,
∴CD是⊙O的切线;
(2)证明:∵∠DCO=90°,
∴∠DCE+∠ACO=90°,
又∵OD⊥AB,
∴∠AEO+∠A=90°,
又∵∠A=∠ACO,∠DEC=∠AEO,
∴∠DEC=∠DCE,
∴DE=DC;
(3)解:∵∠DCO=90°,OD=5,DC=3,
∴OC===4,
∴OA=OC=4,
又DE=DC=3,
∴OE=OD﹣DE=2,
在Rt△AEO中,由勾股定理得:AE2=OA2+OE2=42+22=20,
∴AE=2.
26.(2020秋 大冶市期末)如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D、过D作直线DG∥BC.
(1)求证:DG是⊙O的切线;
(2)求证:DE=CD;
(3)若DE=2,BC=8,求⊙O的半径.
【解析】(1)证明:连接OD交BC于H,如图,
∵点E是△ABC的内心
∴AD平分∠BAC,
即∠BAD=∠CAD,
∴,
∴OD⊥BC,BH=CH,
∵DG∥BC,
∴OD⊥DG,
∴DG是⊙O的切线;
(2)证明:连接BD,
∵点E是△ABC的内心,
∴∠ABE=∠CBE,
∵∠DBC=∠BAD,
∴∠DEB=∠BAD+∠ABE=∠DBC+∠CBE=∠DBE,
即∠BED=∠DBE,
∴BD=DE,
∵,
∴BD=CD,
∴DE=CD;
(3)解:连接OD,OB,如图,
由(1)得OD⊥BC,BH=CH,
∵BC=8,
∴BH=CH=4,
∵DE=2,BD=DE,
∴BD=2,
在Rt△BHD中,BD2=BH2+HD2,
∴(2)2=42+HD2,解得:HD=2,
在Rt△BHO中,
r2=BH2+(r﹣2)2,解得:r=5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
