2021-2022学年人教版九年级上 24.3正多边形和圆同步练习(含解析)
文档属性
| 名称 | 2021-2022学年人教版九年级上 24.3正多边形和圆同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 07:48:57 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版九年级上 24.3正多边形和圆同步练习
一.选择题
1.(2021秋 镇江期中)如图,⊙O是正五边形ABCDE的外接圆,则∠ADE的度数为( )
A.40° B.36° C.32° D.30°
2.(2021 广陵区校级三模)如图,⊙O是正五边形ABCDE的外接圆,点P为上的一点,则∠APC的度数为( )
A.36° B.60° C.72° D.75°
3.(2021秋 江阴市期中)若正六边形的周长为24,则它的外接圆的半径为( )
A.4 B.4 C.2 D.2
4.(2020秋 斗门区期末)若正六边形的边长为4,则它的外接圆的半径为( )
A.4 B.4 C.2 D.2
5.(2021春 迁安市期末)一个正多边形的边长为2,它的内角和是外角和的3倍,则这个多边形的周长是( )
A.6 B.8 C.12 D.16
6.(2021 贵阳)如图,⊙O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC的度数是( )
A.144° B.130° C.129° D.108°
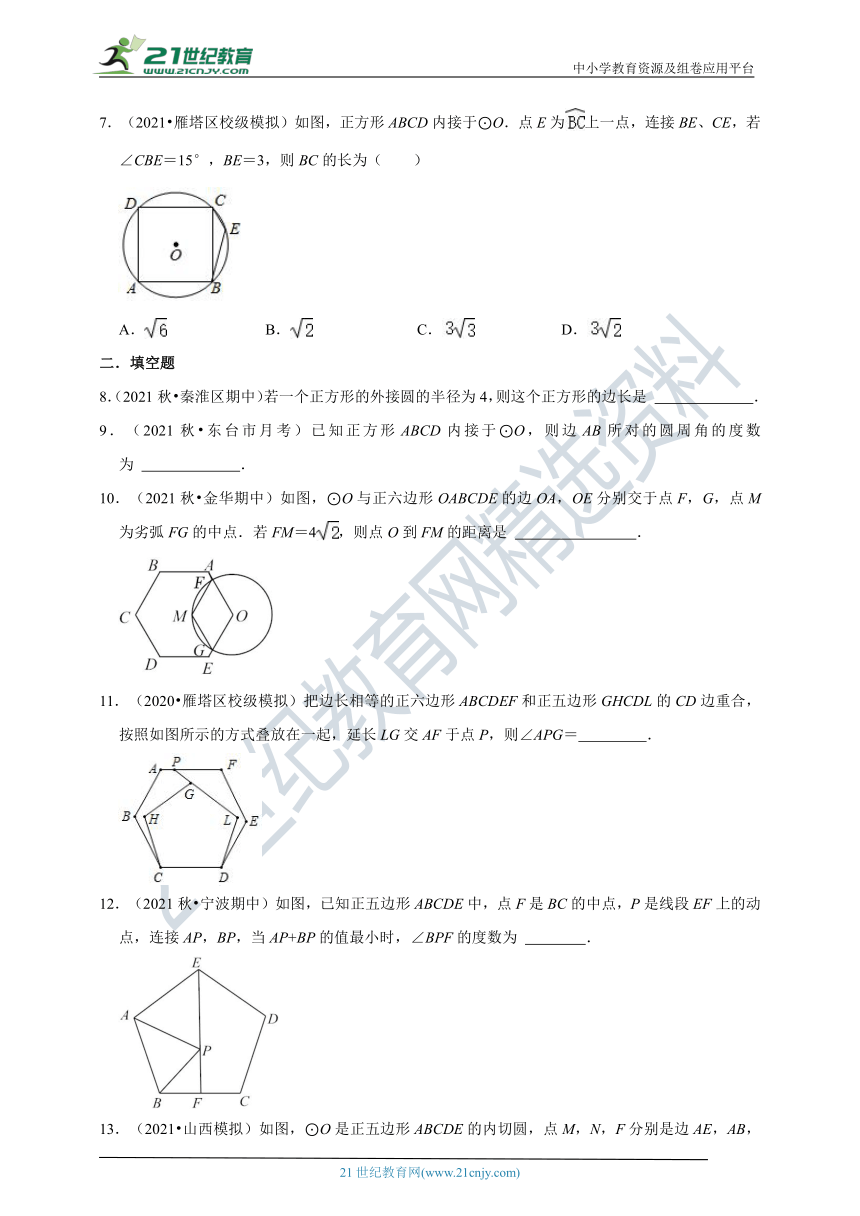
7.(2021 雁塔区校级模拟)如图,正方形ABCD内接于⊙O.点E为上一点,连接BE、CE,若∠CBE=15°,BE=3,则BC的长为( )
A. B. C. D.
二.填空题
8.(2021秋 秦淮区期中)若一个正方形的外接圆的半径为4,则这个正方形的边长是 .
9.(2021秋 东台市月考)已知正方形ABCD内接于⊙O,则边AB所对的圆周角的度数为 .
10.(2021秋 金华期中)如图,⊙O与正六边形OABCDE的边OA,OE分别交于点F,G,点M为劣弧FG的中点.若FM=4,则点O到FM的距离是 .
11.(2020 雁塔区校级模拟)把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合,按照如图所示的方式叠放在一起,延长LG交AF于点P,则∠APG= .
12.(2021秋 宁波期中)如图,已知正五边形ABCDE中,点F是BC的中点,P是线段EF上的动点,连接AP,BP,当AP+BP的值最小时,∠BPF的度数为 .
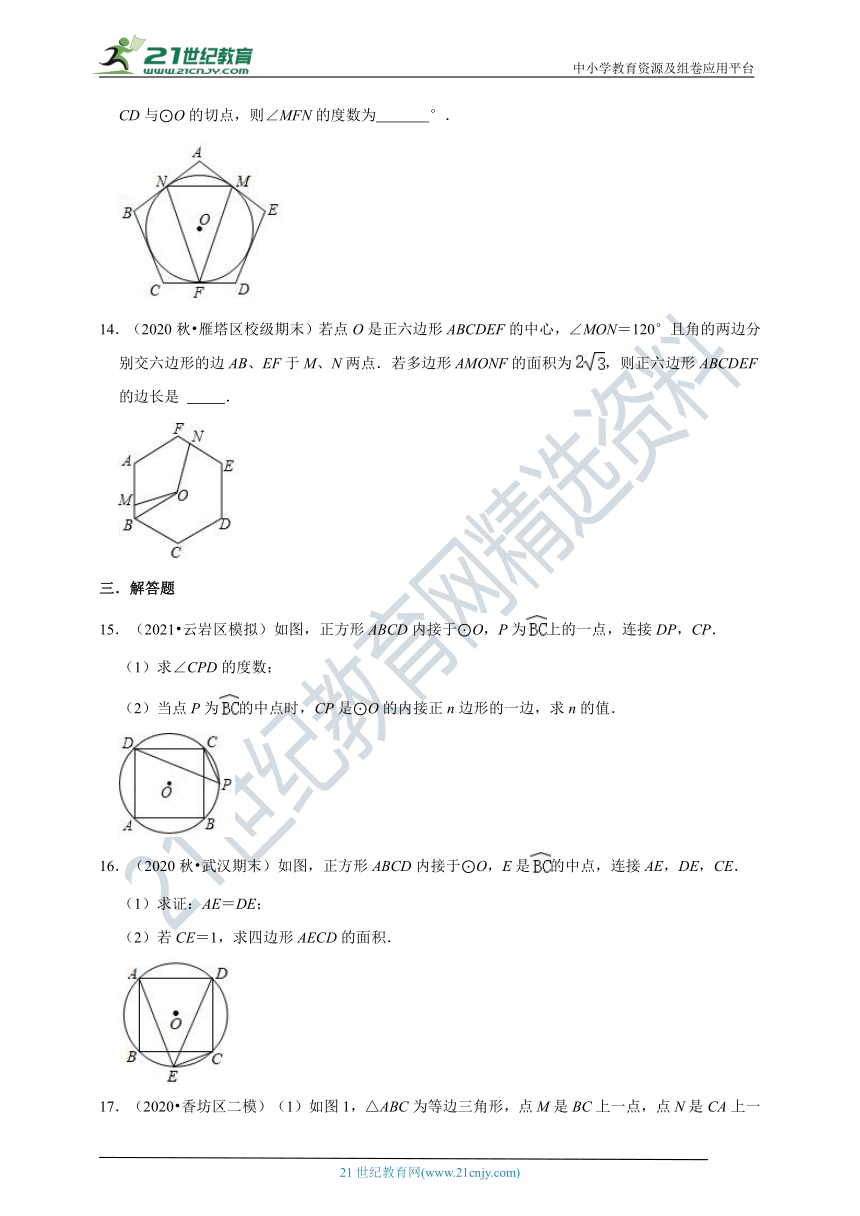
13.(2021 山西模拟)如图,⊙O是正五边形ABCDE的内切圆,点M,N,F分别是边AE,AB,CD与⊙O的切点,则∠MFN的度数为 °.
14.(2020秋 雁塔区校级期末)若点O是正六边形ABCDEF的中心,∠MON=120°且角的两边分别交六边形的边AB、EF于M、N两点.若多边形AMONF的面积为,则正六边形ABCDEF的边长是 .
三.解答题
15.(2021 云岩区模拟)如图,正方形ABCD内接于⊙O,P为上的一点,连接DP,CP.
(1)求∠CPD的度数;
(2)当点P为的中点时,CP是⊙O的内接正n边形的一边,求n的值.
16.(2020秋 武汉期末)如图,正方形ABCD内接于⊙O,E是的中点,连接AE,DE,CE.
(1)求证:AE=DE;
(2)若CE=1,求四边形AECD的面积.
17.(2020 香坊区二模)(1)如图1,△ABC为等边三角形,点M是BC上一点,点N是CA上一点,BM=CN,BN、AM相交于点Q,求∠BQM的度数;
(2)当(1)中的“等边△ABC”的边数逐渐增加,分别变为正方形ABCD(如图2)、正五边形ABCDE(如图3)、正六边形ABCDEF(如图4)…,“点N是CA上一点”变为点N是CD上一点,其余条件不变,分别确定∠BQM的度数,并直接将结论填入下表:
正多边形 正方形 正五边形 正六边形 … 正n边形
∠BQM的度数 …
18.(2020秋 庐阳区期末)已知,正方形ABCD内接于⊙O,点P是弧AD上一点.
(1)如图1,若点P是弧AD的中点,求证:CE=CD;
(2)如图2,若图中PE=OE,求的值.
答案与解析
一.选择题
1.(2021秋 镇江期中)如图,⊙O是正五边形ABCDE的外接圆,则∠ADE的度数为( )
A.40° B.36° C.32° D.30°
【解析】解:如图:连接AO、EO,
在正五边形ABCDE中,∠AOE==72°,
∴∠ADE=∠AOE=×72°=36°,
故选:B.
2.(2021 广陵区校级三模)如图,⊙O是正五边形ABCDE的外接圆,点P为上的一点,则∠APC的度数为( )
A.36° B.60° C.72° D.75°
【解析】解:如图,连接OA,OC,
∵ABCDE是正五边形,
∴∠AOC=×2=144°,
∴∠APC=∠AOC=72°,
故选:C.
3.(2021秋 江阴市期中)若正六边形的周长为24,则它的外接圆的半径为( )
A.4 B.4 C.2 D.2
【解析】解:如图,
∵⊙O的内接正六边形ABCDEF的周长为24,
∴边长为4;
∵∠AOB=×360°=60°,且OA=OB,
∴△OAB为等边三角形,
∴OA=AB=4,
即该圆的半径为4,
故选:B.
4.(2020秋 斗门区期末)若正六边形的边长为4,则它的外接圆的半径为( )
A.4 B.4 C.2 D.2
【解析】解:连接OA、OB,
∵六边形ABCDEF是⊙O的内接正六边形,
∴∠AOB==60°,
∵OA=OB,
∴△AOB是等边三角形,
∵AB=4,
∴OA=OB=AB=4,
即正六边形ABCDEF的外接圆的半径是4,
故选:B.
5.(2021春 迁安市期末)一个正多边形的边长为2,它的内角和是外角和的3倍,则这个多边形的周长是( )
A.6 B.8 C.12 D.16
【解析】解:设正多边形的边数为n,由题意得:
(n﹣2) 180°=3×360°,
解得:n=8,
∵这个正多边形的边长为2,
∴这个正多边形的周长为16.
故选:D.
6.(2021 贵阳)如图,⊙O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC的度数是( )
A.144° B.130° C.129° D.108°
【解析】解:正五边形的内角=(5﹣2)×180°÷5=108°,
∴∠E=∠D=108°,
∵AE、CD分别与⊙O相切于A、C两点,
∴∠OAE=∠OCD=90°,
∴∠AOC=540°﹣90°﹣90°﹣108°﹣108°=144°,
故选:A.
7.(2021 雁塔区校级模拟)如图,正方形ABCD内接于⊙O.点E为上一点,连接BE、CE,若∠CBE=15°,BE=3,则BC的长为( )
A. B. C. D.
【解析】解:连接OA,OB,OE,
∵正方形ABCD内接于⊙O,
∴OA=OB=OE,∠AOB==90°,AB=BC,∠ABC=90°,
∴∠OAB=∠OBA=(180°﹣∠AOB)=45°,
∴∠OBC=∠ABC﹣∠OBA=45°,
∵∠CBE=15°,
∴∠OBE=∠OBC+∠CBE=60°,
∴△OBE是等边三角形,
∴OB=BE=3,
∴OA=3,
∴AB==3,
∴BC=3,
故选:D.
二.填空题
8.(2021秋 秦淮区期中)若一个正方形的外接圆的半径为4,则这个正方形的边长是 4 .
【解析】解:如图所示:
∵四边形ABCD是正方形,
∴∠B=90°,AB=BC,
∴AC是⊙O的直径,△ABC是等腰直角三角形,
∴AC=8,AB=BC=AC=4,
故答案为:4.
9.(2021秋 东台市月考)已知正方形ABCD内接于⊙O,则边AB所对的圆周角的度数为 45°或135° .
【解析】解:圆内接正方形的边BC所对的圆心角360°÷4=90°,则360°﹣90°=270°,
根据圆周角等于同弧所对圆心角的一半,
BC所对的圆周角的度数是90×=45°或270°×=135°.
故答案为45°或135°.
10.(2021秋 金华期中)如图,⊙O与正六边形OABCDE的边OA,OE分别交于点F,G,点M为劣弧FG的中点.若FM=4,则点O到FM的距离是 2 .
【解析】解:连接OM,过O作OH⊥FM于H,
∵正六边形OABCDE,
∴∠FOG=120°,
∵点M为劣弧FG的中点,
∴∠FOM=60°,
∵OH⊥FM,OF=OM,
∴∠OFH=60°,∠OHF=90°,FH=FM=2,
∴OH=FH=2,
故答案为:2.
11.(2020 雁塔区校级模拟)把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合,按照如图所示的方式叠放在一起,延长LG交AF于点P,则∠APG= 144° .
【解析】解:∵六边形ABCDEF,
∴∠A=∠B=∠BCD=,
∵五边形GHCDL是正五边形,
∴∠CDL=∠L=,
∵∠A+∠B+∠BCD+∠CDL+∠L+∠APG=(6﹣2)×180°=720°,
∴∠APG=720°﹣120°×3﹣108°×2=144°,
故答案为:144°.
12.(2021秋 宁波期中)如图,已知正五边形ABCDE中,点F是BC的中点,P是线段EF上的动点,连接AP,BP,当AP+BP的值最小时,∠BPF的度数为 54° .
【解析】解:如图,连接AC,PC,设AC交EF于点P′,连接BP′.
∵正五边形ABCDE中,点F是BC的中点,
∵EF⊥BC,
∴B,C关于EF对称,
∴PB=PC,
∵PA+PB=PA+PC≥AC,
∴当点P与P′重合时,PA+PB的值最小,
∵ABCDE是正五边形,
∴BA=BC,∠ABC=108°,
∴∠BAC=∠BCA=36°,
∵P′B=CP′,
∴∠P′BC=∠P′CB=36°,
∵∠EFB=90°,
∴∠BP′F=90°﹣∠P′BC=90°﹣36°=54°.
故答案为:54°.
13.(2021 山西模拟)如图,⊙O是正五边形ABCDE的内切圆,点M,N,F分别是边AE,AB,CD与⊙O的切点,则∠MFN的度数为 36 °.
【解析】解:如图,连接OM,ON.
∵M,N,F分别是AE,AB,CD与⊙O的切点,
∴OM⊥AE,ON⊥AB,
∴∠OMA=∠ONA=90°,
∵∠A=108°,
∴∠MON=180°﹣108°=72°,
∴∠MFN=∠MON=36°,
故答案为:36.
14.(2020秋 雁塔区校级期末)若点O是正六边形ABCDEF的中心,∠MON=120°且角的两边分别交六边形的边AB、EF于M、N两点.若多边形AMONF的面积为,则正六边形ABCDEF的边长是 2 .
【解析】解:连接OF、OA,作OG⊥AF于点G,如图
正六边形中心角∠AOB==60°,
∴∠BOF=60°×2=120°,∠OFE=∠OBA=60°,OF=AF=OA,
∴∠MON﹣∠MOF=∠BOF﹣∠MOF,
即∠FON=∠BOM,
在△FON和△BOM中
,
∴△FON≌△BOM(AAS),
∴S△FON=S△BOM,
∴S多边形AMONF=S四边形ABOF=2S△OAF,
在Rt△OFG中,∠OFG=60°,
sin60°=,
∴OG=OF=AF,
∴S△OAF=AF OG=AF2,
即2×AF2=2,
解得AF=2,
故答案为2.
三.解答题
15.(2021 云岩区模拟)如图,正方形ABCD内接于⊙O,P为上的一点,连接DP,CP.
(1)求∠CPD的度数;
(2)当点P为的中点时,CP是⊙O的内接正n边形的一边,求n的值.
【解析】解:(1)连接OD,OC,
∵正方形ABCD内接于⊙O,
∴∠DOC=90°.
∴;
(2)连接PO,OB,
∵正方形ABCD内接于⊙O,
∴∠COB=90°,
∵点P为BC的中点,
∴=,
∴,
∴n=360÷45=8.
16.(2020秋 武汉期末)如图,正方形ABCD内接于⊙O,E是的中点,连接AE,DE,CE.
(1)求证:AE=DE;
(2)若CE=1,求四边形AECD的面积.
【解析】(1)证明:∵四边形ABCD是正方形,
∴AB=CD,
∴=,
∵E是的中点,
∴=,
∴+=+,即=,
∴AE=DE.
(2)解:连接BD,AO,过点D作DF⊥DE交EC的延长线于F.
∵四边形ABCD是正方形,
∴∠DBC=∠DEC=45°,DA=DC,
∵∠EDF=90°,
∴∠F=∠EDF﹣∠DEF=90°﹣45°=45°,
∴DE=DF,
∵∠AED=∠AOD=45°,
∴∠AED=∠F=45°,
∵∠ADC=∠EDF=90°,
∴∠ADE+∠EDC=∠CDF+∠EDC=90°,
∴∠ADE=∠CDF
在△ADE和△CDF中,
,
∴△ADE≌△CDF(AAS),
∴AE=CF,
∴S△ADE=S△CDF,
∴S四边形AECD=S△DEF,
∵EF=DE=EC+DE,EC=1,
∴1+DE=DE,
∴DE=+1,
∴S四边形AECD=S△DEF=DE2=+.
17.(2020 香坊区二模)(1)如图1,△ABC为等边三角形,点M是BC上一点,点N是CA上一点,BM=CN,BN、AM相交于点Q,求∠BQM的度数;
(2)当(1)中的“等边△ABC”的边数逐渐增加,分别变为正方形ABCD(如图2)、正五边形ABCDE(如图3)、正六边形ABCDEF(如图4)…,“点N是CA上一点”变为点N是CD上一点,其余条件不变,分别确定∠BQM的度数,并直接将结论填入下表:
正多边形 正方形 正五边形 正六边形 … 正n边形
∠BQM的度数 90° 108° 120° …
【解析】解:(1)在△ABM与△BCN中,
,
∴△ABM≌△BCN(SAS),
∴∠BAM=∠NBC,
∴∠AQN=∠BAM+∠ABQ,
=∠NBC+∠ABQ
=∠ABM=60°,
∴∠AQN=60°.
(2)由(1)可知,∠AQN=各个多边形的一个角的大小,
所以正方形中∠AQN=90°,
正五边形中∠AQN=108°,
正六边形中∠AQN=120°,
…
正n边形中∠AQN=.
故答案为:90°,108°,120°,.
18.(2020秋 庐阳区期末)已知,正方形ABCD内接于⊙O,点P是弧AD上一点.
(1)如图1,若点P是弧AD的中点,求证:CE=CD;
(2)如图2,若图中PE=OE,求的值.
【解析】(1)证明:如图1,连接DE,
∵四边形ABCD是正方形,
∴AC⊥BD,OB=OD=OC,
∴EB=ED,∠ODC=∠OCD=45°,
∴∠EBD=∠EDB,
∵点P是弧AD的中点,
∴∠PBD=∠ABD=×∠AOD=22.5°,
∴∠EDC=∠CDO+∠ODE=45°+22.5°=67.5°,
∴∠CED=180°﹣DCE﹣∠CDE=180°﹣45°﹣67.5°=67.5°,
∴∠CED=∠EDC,
∴CE=CD;
(2)解:如图2,连接DE,DP,
∵四边形ABCD是正方形,
∴∠BAD=∠EOD=90°,OA=OD,
∴∠P=∠BAD=90°,
∵PE=OE,DE=DE,
∴Rt△PDE≌Rt△ODE(HL),
∴∠PDE=∠2,由(1)知∠1=∠2,
∴∠1=∠2=∠PDE,
∴∠1+∠2+∠PDE=90°,
∴∠2=30°,
∴OE=DE,
∴DE=2OE,
∴OD==OE,
∴=,
∴OD=OA=OE,
∴AE=OA﹣OE=(﹣1)OE,EC=OE+OC=(+1)OE,
∴==2﹣.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级上 24.3正多边形和圆同步练习
一.选择题
1.(2021秋 镇江期中)如图,⊙O是正五边形ABCDE的外接圆,则∠ADE的度数为( )
A.40° B.36° C.32° D.30°
2.(2021 广陵区校级三模)如图,⊙O是正五边形ABCDE的外接圆,点P为上的一点,则∠APC的度数为( )
A.36° B.60° C.72° D.75°
3.(2021秋 江阴市期中)若正六边形的周长为24,则它的外接圆的半径为( )
A.4 B.4 C.2 D.2
4.(2020秋 斗门区期末)若正六边形的边长为4,则它的外接圆的半径为( )
A.4 B.4 C.2 D.2
5.(2021春 迁安市期末)一个正多边形的边长为2,它的内角和是外角和的3倍,则这个多边形的周长是( )
A.6 B.8 C.12 D.16
6.(2021 贵阳)如图,⊙O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC的度数是( )
A.144° B.130° C.129° D.108°
7.(2021 雁塔区校级模拟)如图,正方形ABCD内接于⊙O.点E为上一点,连接BE、CE,若∠CBE=15°,BE=3,则BC的长为( )
A. B. C. D.
二.填空题
8.(2021秋 秦淮区期中)若一个正方形的外接圆的半径为4,则这个正方形的边长是 .
9.(2021秋 东台市月考)已知正方形ABCD内接于⊙O,则边AB所对的圆周角的度数为 .
10.(2021秋 金华期中)如图,⊙O与正六边形OABCDE的边OA,OE分别交于点F,G,点M为劣弧FG的中点.若FM=4,则点O到FM的距离是 .
11.(2020 雁塔区校级模拟)把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合,按照如图所示的方式叠放在一起,延长LG交AF于点P,则∠APG= .
12.(2021秋 宁波期中)如图,已知正五边形ABCDE中,点F是BC的中点,P是线段EF上的动点,连接AP,BP,当AP+BP的值最小时,∠BPF的度数为 .
13.(2021 山西模拟)如图,⊙O是正五边形ABCDE的内切圆,点M,N,F分别是边AE,AB,CD与⊙O的切点,则∠MFN的度数为 °.
14.(2020秋 雁塔区校级期末)若点O是正六边形ABCDEF的中心,∠MON=120°且角的两边分别交六边形的边AB、EF于M、N两点.若多边形AMONF的面积为,则正六边形ABCDEF的边长是 .
三.解答题
15.(2021 云岩区模拟)如图,正方形ABCD内接于⊙O,P为上的一点,连接DP,CP.
(1)求∠CPD的度数;
(2)当点P为的中点时,CP是⊙O的内接正n边形的一边,求n的值.
16.(2020秋 武汉期末)如图,正方形ABCD内接于⊙O,E是的中点,连接AE,DE,CE.
(1)求证:AE=DE;
(2)若CE=1,求四边形AECD的面积.
17.(2020 香坊区二模)(1)如图1,△ABC为等边三角形,点M是BC上一点,点N是CA上一点,BM=CN,BN、AM相交于点Q,求∠BQM的度数;
(2)当(1)中的“等边△ABC”的边数逐渐增加,分别变为正方形ABCD(如图2)、正五边形ABCDE(如图3)、正六边形ABCDEF(如图4)…,“点N是CA上一点”变为点N是CD上一点,其余条件不变,分别确定∠BQM的度数,并直接将结论填入下表:
正多边形 正方形 正五边形 正六边形 … 正n边形
∠BQM的度数 …
18.(2020秋 庐阳区期末)已知,正方形ABCD内接于⊙O,点P是弧AD上一点.
(1)如图1,若点P是弧AD的中点,求证:CE=CD;
(2)如图2,若图中PE=OE,求的值.
答案与解析
一.选择题
1.(2021秋 镇江期中)如图,⊙O是正五边形ABCDE的外接圆,则∠ADE的度数为( )
A.40° B.36° C.32° D.30°
【解析】解:如图:连接AO、EO,
在正五边形ABCDE中,∠AOE==72°,
∴∠ADE=∠AOE=×72°=36°,
故选:B.
2.(2021 广陵区校级三模)如图,⊙O是正五边形ABCDE的外接圆,点P为上的一点,则∠APC的度数为( )
A.36° B.60° C.72° D.75°
【解析】解:如图,连接OA,OC,
∵ABCDE是正五边形,
∴∠AOC=×2=144°,
∴∠APC=∠AOC=72°,
故选:C.
3.(2021秋 江阴市期中)若正六边形的周长为24,则它的外接圆的半径为( )
A.4 B.4 C.2 D.2
【解析】解:如图,
∵⊙O的内接正六边形ABCDEF的周长为24,
∴边长为4;
∵∠AOB=×360°=60°,且OA=OB,
∴△OAB为等边三角形,
∴OA=AB=4,
即该圆的半径为4,
故选:B.
4.(2020秋 斗门区期末)若正六边形的边长为4,则它的外接圆的半径为( )
A.4 B.4 C.2 D.2
【解析】解:连接OA、OB,
∵六边形ABCDEF是⊙O的内接正六边形,
∴∠AOB==60°,
∵OA=OB,
∴△AOB是等边三角形,
∵AB=4,
∴OA=OB=AB=4,
即正六边形ABCDEF的外接圆的半径是4,
故选:B.
5.(2021春 迁安市期末)一个正多边形的边长为2,它的内角和是外角和的3倍,则这个多边形的周长是( )
A.6 B.8 C.12 D.16
【解析】解:设正多边形的边数为n,由题意得:
(n﹣2) 180°=3×360°,
解得:n=8,
∵这个正多边形的边长为2,
∴这个正多边形的周长为16.
故选:D.
6.(2021 贵阳)如图,⊙O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC的度数是( )
A.144° B.130° C.129° D.108°
【解析】解:正五边形的内角=(5﹣2)×180°÷5=108°,
∴∠E=∠D=108°,
∵AE、CD分别与⊙O相切于A、C两点,
∴∠OAE=∠OCD=90°,
∴∠AOC=540°﹣90°﹣90°﹣108°﹣108°=144°,
故选:A.
7.(2021 雁塔区校级模拟)如图,正方形ABCD内接于⊙O.点E为上一点,连接BE、CE,若∠CBE=15°,BE=3,则BC的长为( )
A. B. C. D.
【解析】解:连接OA,OB,OE,
∵正方形ABCD内接于⊙O,
∴OA=OB=OE,∠AOB==90°,AB=BC,∠ABC=90°,
∴∠OAB=∠OBA=(180°﹣∠AOB)=45°,
∴∠OBC=∠ABC﹣∠OBA=45°,
∵∠CBE=15°,
∴∠OBE=∠OBC+∠CBE=60°,
∴△OBE是等边三角形,
∴OB=BE=3,
∴OA=3,
∴AB==3,
∴BC=3,
故选:D.
二.填空题
8.(2021秋 秦淮区期中)若一个正方形的外接圆的半径为4,则这个正方形的边长是 4 .
【解析】解:如图所示:
∵四边形ABCD是正方形,
∴∠B=90°,AB=BC,
∴AC是⊙O的直径,△ABC是等腰直角三角形,
∴AC=8,AB=BC=AC=4,
故答案为:4.
9.(2021秋 东台市月考)已知正方形ABCD内接于⊙O,则边AB所对的圆周角的度数为 45°或135° .
【解析】解:圆内接正方形的边BC所对的圆心角360°÷4=90°,则360°﹣90°=270°,
根据圆周角等于同弧所对圆心角的一半,
BC所对的圆周角的度数是90×=45°或270°×=135°.
故答案为45°或135°.
10.(2021秋 金华期中)如图,⊙O与正六边形OABCDE的边OA,OE分别交于点F,G,点M为劣弧FG的中点.若FM=4,则点O到FM的距离是 2 .
【解析】解:连接OM,过O作OH⊥FM于H,
∵正六边形OABCDE,
∴∠FOG=120°,
∵点M为劣弧FG的中点,
∴∠FOM=60°,
∵OH⊥FM,OF=OM,
∴∠OFH=60°,∠OHF=90°,FH=FM=2,
∴OH=FH=2,
故答案为:2.
11.(2020 雁塔区校级模拟)把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合,按照如图所示的方式叠放在一起,延长LG交AF于点P,则∠APG= 144° .
【解析】解:∵六边形ABCDEF,
∴∠A=∠B=∠BCD=,
∵五边形GHCDL是正五边形,
∴∠CDL=∠L=,
∵∠A+∠B+∠BCD+∠CDL+∠L+∠APG=(6﹣2)×180°=720°,
∴∠APG=720°﹣120°×3﹣108°×2=144°,
故答案为:144°.
12.(2021秋 宁波期中)如图,已知正五边形ABCDE中,点F是BC的中点,P是线段EF上的动点,连接AP,BP,当AP+BP的值最小时,∠BPF的度数为 54° .
【解析】解:如图,连接AC,PC,设AC交EF于点P′,连接BP′.
∵正五边形ABCDE中,点F是BC的中点,
∵EF⊥BC,
∴B,C关于EF对称,
∴PB=PC,
∵PA+PB=PA+PC≥AC,
∴当点P与P′重合时,PA+PB的值最小,
∵ABCDE是正五边形,
∴BA=BC,∠ABC=108°,
∴∠BAC=∠BCA=36°,
∵P′B=CP′,
∴∠P′BC=∠P′CB=36°,
∵∠EFB=90°,
∴∠BP′F=90°﹣∠P′BC=90°﹣36°=54°.
故答案为:54°.
13.(2021 山西模拟)如图,⊙O是正五边形ABCDE的内切圆,点M,N,F分别是边AE,AB,CD与⊙O的切点,则∠MFN的度数为 36 °.
【解析】解:如图,连接OM,ON.
∵M,N,F分别是AE,AB,CD与⊙O的切点,
∴OM⊥AE,ON⊥AB,
∴∠OMA=∠ONA=90°,
∵∠A=108°,
∴∠MON=180°﹣108°=72°,
∴∠MFN=∠MON=36°,
故答案为:36.
14.(2020秋 雁塔区校级期末)若点O是正六边形ABCDEF的中心,∠MON=120°且角的两边分别交六边形的边AB、EF于M、N两点.若多边形AMONF的面积为,则正六边形ABCDEF的边长是 2 .
【解析】解:连接OF、OA,作OG⊥AF于点G,如图
正六边形中心角∠AOB==60°,
∴∠BOF=60°×2=120°,∠OFE=∠OBA=60°,OF=AF=OA,
∴∠MON﹣∠MOF=∠BOF﹣∠MOF,
即∠FON=∠BOM,
在△FON和△BOM中
,
∴△FON≌△BOM(AAS),
∴S△FON=S△BOM,
∴S多边形AMONF=S四边形ABOF=2S△OAF,
在Rt△OFG中,∠OFG=60°,
sin60°=,
∴OG=OF=AF,
∴S△OAF=AF OG=AF2,
即2×AF2=2,
解得AF=2,
故答案为2.
三.解答题
15.(2021 云岩区模拟)如图,正方形ABCD内接于⊙O,P为上的一点,连接DP,CP.
(1)求∠CPD的度数;
(2)当点P为的中点时,CP是⊙O的内接正n边形的一边,求n的值.
【解析】解:(1)连接OD,OC,
∵正方形ABCD内接于⊙O,
∴∠DOC=90°.
∴;
(2)连接PO,OB,
∵正方形ABCD内接于⊙O,
∴∠COB=90°,
∵点P为BC的中点,
∴=,
∴,
∴n=360÷45=8.
16.(2020秋 武汉期末)如图,正方形ABCD内接于⊙O,E是的中点,连接AE,DE,CE.
(1)求证:AE=DE;
(2)若CE=1,求四边形AECD的面积.
【解析】(1)证明:∵四边形ABCD是正方形,
∴AB=CD,
∴=,
∵E是的中点,
∴=,
∴+=+,即=,
∴AE=DE.
(2)解:连接BD,AO,过点D作DF⊥DE交EC的延长线于F.
∵四边形ABCD是正方形,
∴∠DBC=∠DEC=45°,DA=DC,
∵∠EDF=90°,
∴∠F=∠EDF﹣∠DEF=90°﹣45°=45°,
∴DE=DF,
∵∠AED=∠AOD=45°,
∴∠AED=∠F=45°,
∵∠ADC=∠EDF=90°,
∴∠ADE+∠EDC=∠CDF+∠EDC=90°,
∴∠ADE=∠CDF
在△ADE和△CDF中,
,
∴△ADE≌△CDF(AAS),
∴AE=CF,
∴S△ADE=S△CDF,
∴S四边形AECD=S△DEF,
∵EF=DE=EC+DE,EC=1,
∴1+DE=DE,
∴DE=+1,
∴S四边形AECD=S△DEF=DE2=+.
17.(2020 香坊区二模)(1)如图1,△ABC为等边三角形,点M是BC上一点,点N是CA上一点,BM=CN,BN、AM相交于点Q,求∠BQM的度数;
(2)当(1)中的“等边△ABC”的边数逐渐增加,分别变为正方形ABCD(如图2)、正五边形ABCDE(如图3)、正六边形ABCDEF(如图4)…,“点N是CA上一点”变为点N是CD上一点,其余条件不变,分别确定∠BQM的度数,并直接将结论填入下表:
正多边形 正方形 正五边形 正六边形 … 正n边形
∠BQM的度数 90° 108° 120° …
【解析】解:(1)在△ABM与△BCN中,
,
∴△ABM≌△BCN(SAS),
∴∠BAM=∠NBC,
∴∠AQN=∠BAM+∠ABQ,
=∠NBC+∠ABQ
=∠ABM=60°,
∴∠AQN=60°.
(2)由(1)可知,∠AQN=各个多边形的一个角的大小,
所以正方形中∠AQN=90°,
正五边形中∠AQN=108°,
正六边形中∠AQN=120°,
…
正n边形中∠AQN=.
故答案为:90°,108°,120°,.
18.(2020秋 庐阳区期末)已知,正方形ABCD内接于⊙O,点P是弧AD上一点.
(1)如图1,若点P是弧AD的中点,求证:CE=CD;
(2)如图2,若图中PE=OE,求的值.
【解析】(1)证明:如图1,连接DE,
∵四边形ABCD是正方形,
∴AC⊥BD,OB=OD=OC,
∴EB=ED,∠ODC=∠OCD=45°,
∴∠EBD=∠EDB,
∵点P是弧AD的中点,
∴∠PBD=∠ABD=×∠AOD=22.5°,
∴∠EDC=∠CDO+∠ODE=45°+22.5°=67.5°,
∴∠CED=180°﹣DCE﹣∠CDE=180°﹣45°﹣67.5°=67.5°,
∴∠CED=∠EDC,
∴CE=CD;
(2)解:如图2,连接DE,DP,
∵四边形ABCD是正方形,
∴∠BAD=∠EOD=90°,OA=OD,
∴∠P=∠BAD=90°,
∵PE=OE,DE=DE,
∴Rt△PDE≌Rt△ODE(HL),
∴∠PDE=∠2,由(1)知∠1=∠2,
∴∠1=∠2=∠PDE,
∴∠1+∠2+∠PDE=90°,
∴∠2=30°,
∴OE=DE,
∴DE=2OE,
∴OD==OE,
∴=,
∴OD=OA=OE,
∴AE=OA﹣OE=(﹣1)OE,EC=OE+OC=(+1)OE,
∴==2﹣.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
