五年级上册数学 整数乘法运算定律推广到小数-小小采购员 课件(26张PPT)
文档属性
| 名称 | 五年级上册数学 整数乘法运算定律推广到小数-小小采购员 课件(26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 17:08:18 | ||
图片预览




文档简介
(共26张PPT)
小小采购员
—整数乘法运算定律推广到小数
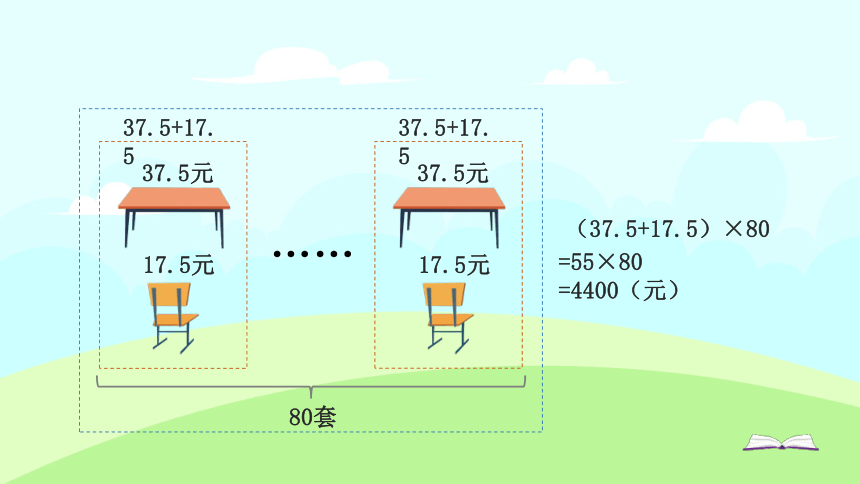
学校要添置80套单人课桌椅,每张课桌37.5元,每把椅子17.5元。添置这些课桌椅一共需要多少元钱?
……
37.5元
37.5元
80张
37.5×80
37.5×80
……
37.5元
37.5元
80张
80把
……
17.5元
17.5元
17.5×80
=3000+1400
=4400(元)
……
37.5元
37.5元
80张
80把
……
17.5元
17.5元
37.5×80+17.5×80
17.5元
37.5元
37.5+17.5
17.5元
37.5元
37.5+17.5
……
17.5元
37.5元
37.5+17.5
80套
(37.5+17.5)×80
=55×80
=4400(元)
(37.5+17.5)×80
=55×80
=4400(元)
=3000+1400
=4400(元)
37.5×80+17.5×80
学校要添置80套单人课桌椅,每张课桌37.5元,每把椅子17.5元。添置这些课桌椅一共需要多少元钱?
方法一:
方法二:
答:添置这些课桌椅一共需要4400元。
=
乘法分配律 适用 于小数
37.5×80+17.5×80
(37.5+17.5)×80
类比 与 迁移
乘法交换律
乘法结合律
乘法分配律
整数
适用于小数
乘法交换律
乘法结合律
乘法分配律
简算
4×4.3×0.25
组合凑整
乘法交换律
乘法结合律
乘法分配律
简算
4×4.3×0.25
组合凑整
=4×0.25×4.3
=1×4.3
=4.3
乘法交换律
乘法结合律
乘法分配律
简算
99×5.2
数字拆合
乘法交换律
乘法结合律
乘法分配律
简算
99×5.2
数字拆合
=(100-1)×5.2
=100×5.2-1×5.2
=520-5.2
=514.8
=0.25×0.4×0.6×8×1.25
0.25×4.8×0.4×1.25
数字拆合
=(0.25×0.4)×0.6×(8×1.25)
=0.1×0.6×10
=0.6
=0.25×0.4×0.6×8×1.25
0.25×4.8×0.4×1.25
组合凑整
=(0.25×0.4)×0.6×(8×1.25)
=0.1×0.6×10
=0.6
=0.25×0.4×0.6×8×1.25
0.25×4.8×0.4×1.25
难点点拨
根据需要拆分因数,但不能改变因数大小
10.5×8.3+10.5×1.7
98×0.85
=10.5×(8.3+1.7)
=10.5×10
=105
=(100-2)×0.85
=100×0.85- 2×0.85
=85-1.7
=83.3
组合凑整
98×0.85
=(100-2)×0.85
=100×0.85- 2×0.85
=85-1.7
=83.3
重点提示
乘法分配律不但可以逆用,还可以推广到求两积之差的简算中。
10.5×8.3+10.5×1.7
=10.5×(8.3+1.7)
=10.5×10
=105
98×0.85
=(100-2)×0.85
=100×0.85- 2×0.85
=85-1.7
=83.3
易错提示
运用乘法分配律时,公共的因数要和括号内的每一个数相乘。
3.29×99+3.29
=3.29×99+3.29×1
数字拆合
3.29×99+3.29
=3.29×99+3.29×1
=3.29×(99+1)
=3.29×100
=329
组合凑整
3.8×0.67+ 0.38×4.2 - 0.038×9
=3.8×0.67+ 3.8×0.42 - 3.8×0.09
积不变规律
积不变规律
3.8×0.67+ 0.38×4.2 - 0.038×9
=3.8×0.67+ 3.8×0.42 - 3.8×0.09
=3.8×(0.67+0.42-0.09)
=3.8×1
=3.8
组合凑整
3.8×0.67+ 0.38×4.2 - 0.038×9
=3.8×0.67+ 3.8×0.42 - 3.8×0.09
=3.8×(0.67+0.42-0.09)
=3.8×1
=3.8
方法总结
因数有相同数字
1.先利用积不变规律,使因
数相同;
2.再逆用乘法分配律简算。
下次再见
小小采购员
—整数乘法运算定律推广到小数
学校要添置80套单人课桌椅,每张课桌37.5元,每把椅子17.5元。添置这些课桌椅一共需要多少元钱?
……
37.5元
37.5元
80张
37.5×80
37.5×80
……
37.5元
37.5元
80张
80把
……
17.5元
17.5元
17.5×80
=3000+1400
=4400(元)
……
37.5元
37.5元
80张
80把
……
17.5元
17.5元
37.5×80+17.5×80
17.5元
37.5元
37.5+17.5
17.5元
37.5元
37.5+17.5
……
17.5元
37.5元
37.5+17.5
80套
(37.5+17.5)×80
=55×80
=4400(元)
(37.5+17.5)×80
=55×80
=4400(元)
=3000+1400
=4400(元)
37.5×80+17.5×80
学校要添置80套单人课桌椅,每张课桌37.5元,每把椅子17.5元。添置这些课桌椅一共需要多少元钱?
方法一:
方法二:
答:添置这些课桌椅一共需要4400元。
=
乘法分配律 适用 于小数
37.5×80+17.5×80
(37.5+17.5)×80
类比 与 迁移
乘法交换律
乘法结合律
乘法分配律
整数
适用于小数
乘法交换律
乘法结合律
乘法分配律
简算
4×4.3×0.25
组合凑整
乘法交换律
乘法结合律
乘法分配律
简算
4×4.3×0.25
组合凑整
=4×0.25×4.3
=1×4.3
=4.3
乘法交换律
乘法结合律
乘法分配律
简算
99×5.2
数字拆合
乘法交换律
乘法结合律
乘法分配律
简算
99×5.2
数字拆合
=(100-1)×5.2
=100×5.2-1×5.2
=520-5.2
=514.8
=0.25×0.4×0.6×8×1.25
0.25×4.8×0.4×1.25
数字拆合
=(0.25×0.4)×0.6×(8×1.25)
=0.1×0.6×10
=0.6
=0.25×0.4×0.6×8×1.25
0.25×4.8×0.4×1.25
组合凑整
=(0.25×0.4)×0.6×(8×1.25)
=0.1×0.6×10
=0.6
=0.25×0.4×0.6×8×1.25
0.25×4.8×0.4×1.25
难点点拨
根据需要拆分因数,但不能改变因数大小
10.5×8.3+10.5×1.7
98×0.85
=10.5×(8.3+1.7)
=10.5×10
=105
=(100-2)×0.85
=100×0.85- 2×0.85
=85-1.7
=83.3
组合凑整
98×0.85
=(100-2)×0.85
=100×0.85- 2×0.85
=85-1.7
=83.3
重点提示
乘法分配律不但可以逆用,还可以推广到求两积之差的简算中。
10.5×8.3+10.5×1.7
=10.5×(8.3+1.7)
=10.5×10
=105
98×0.85
=(100-2)×0.85
=100×0.85- 2×0.85
=85-1.7
=83.3
易错提示
运用乘法分配律时,公共的因数要和括号内的每一个数相乘。
3.29×99+3.29
=3.29×99+3.29×1
数字拆合
3.29×99+3.29
=3.29×99+3.29×1
=3.29×(99+1)
=3.29×100
=329
组合凑整
3.8×0.67+ 0.38×4.2 - 0.038×9
=3.8×0.67+ 3.8×0.42 - 3.8×0.09
积不变规律
积不变规律
3.8×0.67+ 0.38×4.2 - 0.038×9
=3.8×0.67+ 3.8×0.42 - 3.8×0.09
=3.8×(0.67+0.42-0.09)
=3.8×1
=3.8
组合凑整
3.8×0.67+ 0.38×4.2 - 0.038×9
=3.8×0.67+ 3.8×0.42 - 3.8×0.09
=3.8×(0.67+0.42-0.09)
=3.8×1
=3.8
方法总结
因数有相同数字
1.先利用积不变规律,使因
数相同;
2.再逆用乘法分配律简算。
下次再见
