2021-2022学年 京改版数学 九年级上册21.4 圆周角 课后习题(Word版含解析)
文档属性
| 名称 | 2021-2022学年 京改版数学 九年级上册21.4 圆周角 课后习题(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 409.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 00:00:00 | ||
图片预览


文档简介
21.4 圆周角
一、单选题
1.如图,△ABC内接于⊙O,∠C=30°,AB=2,则⊙O的半径为( )
A. B. C. D.
2.已知四边形ABCD内接于,,则的度数为( ).
A.30° B.60° C.120° D.140°
3.如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数是( )
A.40 B.80 C.50 D.45
4.如图,点A、B、C在⊙O上,∠ACB=52°,则∠ABO的度数是( )
A.52° B.26° C.38° D.104°
5.如图,已知⊙O的直径AD=10.任一圆周角∠ACB=45°,则弦AB的长为( )
A.5 B.5 C.5 D.5
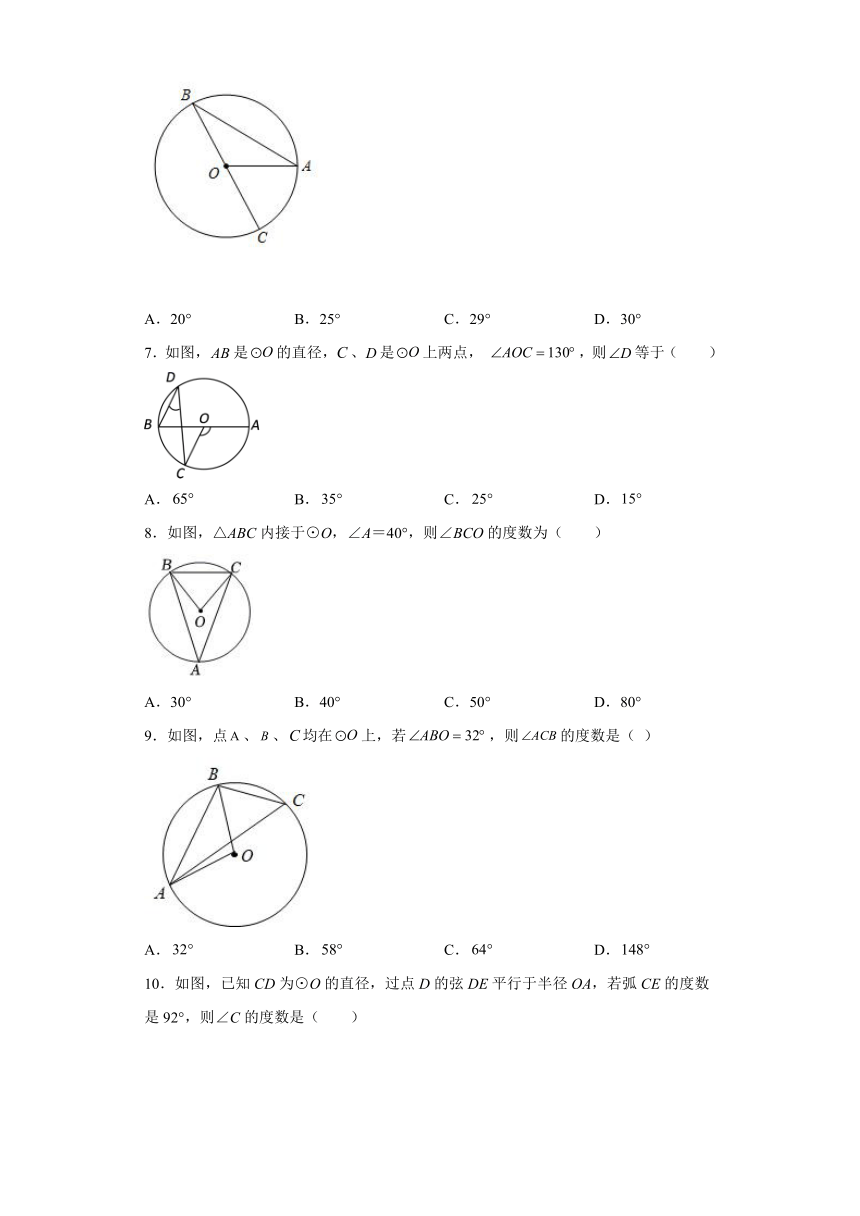
6.如图,BC是⊙O的直径,AB是⊙O的弦,若∠AOC=58°,则∠OAB的度数是( )
A.20° B.25° C.29° D.30°
7.如图,是的直径,、是上两点, ,则等于( )
A. B. C. D.
8.如图,△ABC内接于⊙O,∠A=40°,则∠BCO的度数为( )
A.30° B.40° C.50° D.80°
9.如图,点、、均在上,若,则的度数是( )
A. B. C. D.
10.如图,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若弧CE的度数是92°,则∠C的度数是( )
A.46° B.88° C.24° D.23°
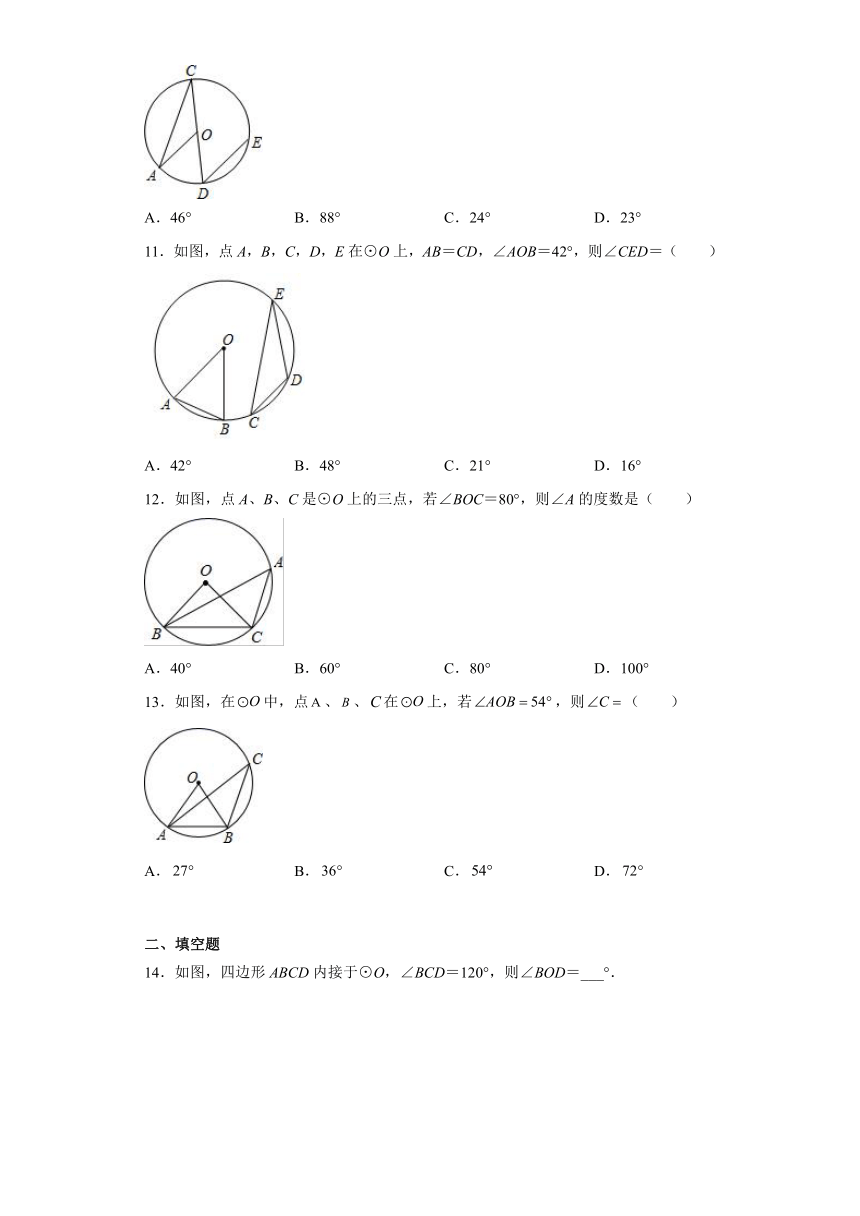
11.如图,点A,B,C,D,E在⊙O上,AB=CD,∠AOB=42°,则∠CED=( )
A.42° B.48° C.21° D.16°
12.如图,点A、B、C是⊙O上的三点,若∠BOC=80°,则∠A的度数是( )
A.40° B.60° C.80° D.100°
13.如图,在中,点、、在上,若,则( )
A. B. C. D.
二、填空题
14.如图,四边形ABCD内接于⊙O,∠BCD=120°,则∠BOD=___°.
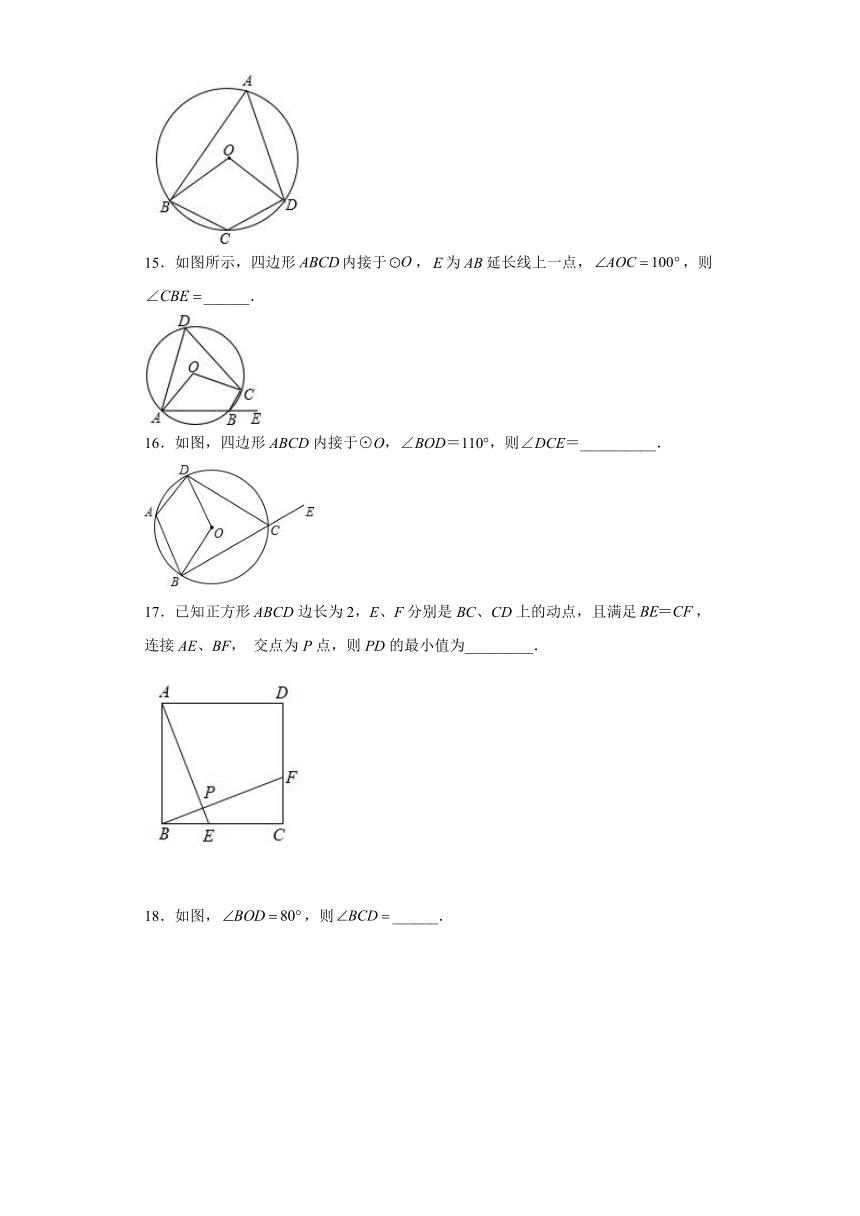
15.如图所示,四边形内接于,为延长线上一点,,则______.
16.如图,四边形ABCD内接于⊙O,∠BOD=110°,则∠DCE=__________.
17.已知正方形ABCD边长为2,E、F分别是BC、CD上的动点,且满足,连接AE、BF, 交点为P点,则PD的最小值为_________.
18.如图,,则______.
19.如图,AB是半圆的直径,C、D是半圆上的两点,∠CAB=24°,则∠ADC的度数为___.
20.如图,为半圆弧的中点,为弧上任意一点,且与交于点,连接. 若,则的最小值为_________
21.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为5,∠B=135°,则弦AC的长为_______.
三、解答题
22.如图,⊙O是三角形ABC的外接圆,AD是⊙O的直径,AD⊥BC于点E.
(1)求证:∠BAD=∠CAD;
(2)若BC长为8,DE=3,求⊙O的半径长.
23.如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,∠EAC=120°.
(1)连OB,OC,求∠BOC;
(2)连DB,DC,求证:DB=DC;
(3)探究线段AD,AB,AC之间的数量关系,并证明你的结论.
24.如图,在△ABC中,AB=AC,以AB为直径作圆O,交BC于点D,交AC于点E.
(1)求证:BD=CD.
(2)若弧DE=50°,求∠C的度数.
参考答案
1.B
解:如图所示,连接OA,OB,
∵∠C=30°,
∴∠OAB=60°,
∵OA=OB,
∴△OAB是等边三角形,
∴OA=AB=2,
∴圆O的半径为2,
故选B.
2.C
解:如图,四边形ABCD内接于,
故选C
3.C
解:∵OB=OC,
∴∠OBC=∠OCB=40°,
∴∠BOC=180° ∠OBC ∠OCB=100°,
∴∠A=∠BOC=50°.
故选:C.
4.C
解:∵∠ACB=52°,
∴∠AOB=2∠ACB=104°,
∵OB=OA,
∴∠ABO=∠BAO=(180°-∠AOB)= (180°-104°)=38°,
故选C.
5.B
解:连接OB.∵∠ACB=45°,
∴∠AOB=2∠ACB=90°,
∵AO=BO=5
∴△AOB是等腰直角三角形
∴AB=.
故选:B.
6.C
∵OA=OB
∴∠OAB=∠OBA
∵∠OBA、∠AOC对着同一段弧
∴
∴∠OAB=29゜
故选:C
7.C
,
,
,
故选:C.
8.C
解:∵△ABC内接于⊙O,
∴∠BOC=2∠A=80°,
∵OB=OC,
∴∠BCO=∠CBO=50°,
故选:C.
9.B
解:∵,
∴,
∴,
∴,
故选:B.
10.D
解:如图,连接OE,
∵弧CE的度数是92°,
∴∠COE=92°,
∴∠CDE=∠COE=46°,
∵OADE,
∴∠AOD=∠CDE=46°,
∴∠C=∠AOD=23°,
故选:D.
11.C
解: 点A、B、C、D、E在上,,,
,
,
故选:C.
12.A
解:∵与是同弧所对的圆心角与圆周角,,
∴,
故选:A.
13.A
解:∵,
∴∠C=.
故答案为:A.
14.
解: 四边形ABCD内接于⊙O,∠BCD=120°,
故答案为:
15.50°
由圆周角定理得,∠D=∠AOC=50°,
由圆内接四边形的性质得,∠CBE=∠D=50°;
答案应为:50°.
16.125°度
解:∵∠BOD=110°,
∴∠,
∴∠DCE=,
故答案为:125°.
17.
解:如图所示:
在正方形ABCD中,,,
在和中,
,
∴ ,
∴,
∵,
∴,
即,
∴,
根据圆周角定理,作一个以AB为直径的圆,角所对的弦是直径,
∴点P在以AB为直径的圆上,如图所示:
∵E、F分别是BC、CD上的动点,
∴当点E到达点C时,此时点F到达点D,此时即为PD的最小值,
在中,,
∴,
∴,
故答案为:.
18.##
解:如图,作圆周角
四边形为的内接四边形,
故答案为:
19.114°
解:连接BD,如图:
∵AB是半圆的直径,
∴∠ADB=90°,
∵∠CAB=∠BDC=24°,
∴∠ADC=∠BDC+∠ADB=24°+90°=114°.
故答案为:114°.
20.
解:如图,设半圆弧所在圆的圆心为,连接,分别过点作的垂线,两垂线交于点,延长至点,使得,连接,
为半圆弧的中点,
,
又,
四边形是正方形,
,
在中,,
,
,
是等腰直角三角形,,
由圆周角定理得:,
,即,
,
,
又,
点四点共圆,且所在圆的圆心为点,
,
由三角形的三边关系定理、两点之间线段最短得:,即,当且仅当点共线时,等号成立,
则的最小值为,
故答案为:.
21.
如图所示,连接、、,
四边形是的内接四边形,
,
,
,
,
的半径为5,
,
故答案为:.
22.(1)见解析;(2)
(1)证明:∵直径AD⊥弦BC
∴弧BD=弧BC,
∵点A在圆上
∴∠BAD=∠CAD;
(2)解:连接OB
∵直径AD⊥弦BC,BC=8
∴BE=4,∠OEB=90°
设圆的半径是x,则OE=x-DE
∵DE=3
∴OE=x-3
由勾股定理得:
∴.
23.(1)120°;(2)见解析;(3)AC=AD+AB,理由见解析.
(1)解:连接OB,OC,
∵∠EAC=120°,
∴∠BAC=60°.
∴∠BDC=∠BAC=60°.
∴∠BOC=2∠BDC=2×60°=120°;
(2)证明:∵AD是△ABC的外角∠EAC的平分线,
∴∠DAC=∠EAC==60°.
∴∠DBC=∠DAC=60°.
由(1)知∠BDC=60°,
∴∠BDC=∠DBC=60°.
∴△BDC是等边三角形.
∴BD=CD;
(3)解:AC=AD+AB,理由如下:
如图,延长AD至F,使DF=AB,连接CF,
∵四边形ABCD是⊙O的内角四边形,
∴∠ADC+∠ABC=180°.
∵∠ADC+∠CDF=180°,
∴∠ABC=∠CDF.
由(2)知△BDC是等边三角形,
∴BC=CD.
∴△FDC≌△ABC(SAS).
∴∠ACB=∠DCF,AC=CF.
∴∠ACF=∠BCD=60°.
∴△ACF是等边三角形.
∴AC=AF=AD+AB.
24.(1)证明过程见解析;(2)65°
(1)证明:连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=DC;
(2)解:连接OE,OD.
∵的度数=50°,
∴∠DOE=50°,
∴∠DAC=∠DOE=25°,
∵AD⊥BC,
∴∠C=90°﹣25°=65°.
一、单选题
1.如图,△ABC内接于⊙O,∠C=30°,AB=2,则⊙O的半径为( )
A. B. C. D.
2.已知四边形ABCD内接于,,则的度数为( ).
A.30° B.60° C.120° D.140°
3.如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数是( )
A.40 B.80 C.50 D.45
4.如图,点A、B、C在⊙O上,∠ACB=52°,则∠ABO的度数是( )
A.52° B.26° C.38° D.104°
5.如图,已知⊙O的直径AD=10.任一圆周角∠ACB=45°,则弦AB的长为( )
A.5 B.5 C.5 D.5
6.如图,BC是⊙O的直径,AB是⊙O的弦,若∠AOC=58°,则∠OAB的度数是( )
A.20° B.25° C.29° D.30°
7.如图,是的直径,、是上两点, ,则等于( )
A. B. C. D.
8.如图,△ABC内接于⊙O,∠A=40°,则∠BCO的度数为( )
A.30° B.40° C.50° D.80°
9.如图,点、、均在上,若,则的度数是( )
A. B. C. D.
10.如图,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若弧CE的度数是92°,则∠C的度数是( )
A.46° B.88° C.24° D.23°
11.如图,点A,B,C,D,E在⊙O上,AB=CD,∠AOB=42°,则∠CED=( )
A.42° B.48° C.21° D.16°
12.如图,点A、B、C是⊙O上的三点,若∠BOC=80°,则∠A的度数是( )
A.40° B.60° C.80° D.100°
13.如图,在中,点、、在上,若,则( )
A. B. C. D.
二、填空题
14.如图,四边形ABCD内接于⊙O,∠BCD=120°,则∠BOD=___°.
15.如图所示,四边形内接于,为延长线上一点,,则______.
16.如图,四边形ABCD内接于⊙O,∠BOD=110°,则∠DCE=__________.
17.已知正方形ABCD边长为2,E、F分别是BC、CD上的动点,且满足,连接AE、BF, 交点为P点,则PD的最小值为_________.
18.如图,,则______.
19.如图,AB是半圆的直径,C、D是半圆上的两点,∠CAB=24°,则∠ADC的度数为___.
20.如图,为半圆弧的中点,为弧上任意一点,且与交于点,连接. 若,则的最小值为_________
21.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为5,∠B=135°,则弦AC的长为_______.
三、解答题
22.如图,⊙O是三角形ABC的外接圆,AD是⊙O的直径,AD⊥BC于点E.
(1)求证:∠BAD=∠CAD;
(2)若BC长为8,DE=3,求⊙O的半径长.
23.如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,∠EAC=120°.
(1)连OB,OC,求∠BOC;
(2)连DB,DC,求证:DB=DC;
(3)探究线段AD,AB,AC之间的数量关系,并证明你的结论.
24.如图,在△ABC中,AB=AC,以AB为直径作圆O,交BC于点D,交AC于点E.
(1)求证:BD=CD.
(2)若弧DE=50°,求∠C的度数.
参考答案
1.B
解:如图所示,连接OA,OB,
∵∠C=30°,
∴∠OAB=60°,
∵OA=OB,
∴△OAB是等边三角形,
∴OA=AB=2,
∴圆O的半径为2,
故选B.
2.C
解:如图,四边形ABCD内接于,
故选C
3.C
解:∵OB=OC,
∴∠OBC=∠OCB=40°,
∴∠BOC=180° ∠OBC ∠OCB=100°,
∴∠A=∠BOC=50°.
故选:C.
4.C
解:∵∠ACB=52°,
∴∠AOB=2∠ACB=104°,
∵OB=OA,
∴∠ABO=∠BAO=(180°-∠AOB)= (180°-104°)=38°,
故选C.
5.B
解:连接OB.∵∠ACB=45°,
∴∠AOB=2∠ACB=90°,
∵AO=BO=5
∴△AOB是等腰直角三角形
∴AB=.
故选:B.
6.C
∵OA=OB
∴∠OAB=∠OBA
∵∠OBA、∠AOC对着同一段弧
∴
∴∠OAB=29゜
故选:C
7.C
,
,
,
故选:C.
8.C
解:∵△ABC内接于⊙O,
∴∠BOC=2∠A=80°,
∵OB=OC,
∴∠BCO=∠CBO=50°,
故选:C.
9.B
解:∵,
∴,
∴,
∴,
故选:B.
10.D
解:如图,连接OE,
∵弧CE的度数是92°,
∴∠COE=92°,
∴∠CDE=∠COE=46°,
∵OADE,
∴∠AOD=∠CDE=46°,
∴∠C=∠AOD=23°,
故选:D.
11.C
解: 点A、B、C、D、E在上,,,
,
,
故选:C.
12.A
解:∵与是同弧所对的圆心角与圆周角,,
∴,
故选:A.
13.A
解:∵,
∴∠C=.
故答案为:A.
14.
解: 四边形ABCD内接于⊙O,∠BCD=120°,
故答案为:
15.50°
由圆周角定理得,∠D=∠AOC=50°,
由圆内接四边形的性质得,∠CBE=∠D=50°;
答案应为:50°.
16.125°度
解:∵∠BOD=110°,
∴∠,
∴∠DCE=,
故答案为:125°.
17.
解:如图所示:
在正方形ABCD中,,,
在和中,
,
∴ ,
∴,
∵,
∴,
即,
∴,
根据圆周角定理,作一个以AB为直径的圆,角所对的弦是直径,
∴点P在以AB为直径的圆上,如图所示:
∵E、F分别是BC、CD上的动点,
∴当点E到达点C时,此时点F到达点D,此时即为PD的最小值,
在中,,
∴,
∴,
故答案为:.
18.##
解:如图,作圆周角
四边形为的内接四边形,
故答案为:
19.114°
解:连接BD,如图:
∵AB是半圆的直径,
∴∠ADB=90°,
∵∠CAB=∠BDC=24°,
∴∠ADC=∠BDC+∠ADB=24°+90°=114°.
故答案为:114°.
20.
解:如图,设半圆弧所在圆的圆心为,连接,分别过点作的垂线,两垂线交于点,延长至点,使得,连接,
为半圆弧的中点,
,
又,
四边形是正方形,
,
在中,,
,
,
是等腰直角三角形,,
由圆周角定理得:,
,即,
,
,
又,
点四点共圆,且所在圆的圆心为点,
,
由三角形的三边关系定理、两点之间线段最短得:,即,当且仅当点共线时,等号成立,
则的最小值为,
故答案为:.
21.
如图所示,连接、、,
四边形是的内接四边形,
,
,
,
,
的半径为5,
,
故答案为:.
22.(1)见解析;(2)
(1)证明:∵直径AD⊥弦BC
∴弧BD=弧BC,
∵点A在圆上
∴∠BAD=∠CAD;
(2)解:连接OB
∵直径AD⊥弦BC,BC=8
∴BE=4,∠OEB=90°
设圆的半径是x,则OE=x-DE
∵DE=3
∴OE=x-3
由勾股定理得:
∴.
23.(1)120°;(2)见解析;(3)AC=AD+AB,理由见解析.
(1)解:连接OB,OC,
∵∠EAC=120°,
∴∠BAC=60°.
∴∠BDC=∠BAC=60°.
∴∠BOC=2∠BDC=2×60°=120°;
(2)证明:∵AD是△ABC的外角∠EAC的平分线,
∴∠DAC=∠EAC==60°.
∴∠DBC=∠DAC=60°.
由(1)知∠BDC=60°,
∴∠BDC=∠DBC=60°.
∴△BDC是等边三角形.
∴BD=CD;
(3)解:AC=AD+AB,理由如下:
如图,延长AD至F,使DF=AB,连接CF,
∵四边形ABCD是⊙O的内角四边形,
∴∠ADC+∠ABC=180°.
∵∠ADC+∠CDF=180°,
∴∠ABC=∠CDF.
由(2)知△BDC是等边三角形,
∴BC=CD.
∴△FDC≌△ABC(SAS).
∴∠ACB=∠DCF,AC=CF.
∴∠ACF=∠BCD=60°.
∴△ACF是等边三角形.
∴AC=AF=AD+AB.
24.(1)证明过程见解析;(2)65°
(1)证明:连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=DC;
(2)解:连接OE,OD.
∵的度数=50°,
∴∠DOE=50°,
∴∠DAC=∠DOE=25°,
∵AD⊥BC,
∴∠C=90°﹣25°=65°.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
