2021-2022学年湖南省邵阳市邵阳县八年级(上)期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年湖南省邵阳市邵阳县八年级(上)期中数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 349.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 00:00:00 | ||
图片预览




文档简介
2021-2022学年湖南省邵阳市邵阳县八年级(上)期中数学试卷
一、选择题(每小题3分,共30分)
1.(3分)下列式子:,,,3x+,中,是分式的有( )
A.2个 B.3个 C.4个 D.5个
2.(3分)如图,AB∥DE,AF=DC,若要证明△ABC≌△DEF,还需补充的条件是( )
A.AC=DF B.AB=DE C.∠A=∠D D.BC=EF
3.(3分)如图,△ABC≌△BAD,点A和点B,点C和点D是对应点.如果∠D=70°,∠CAB=50°,那么∠DAB度数是( )
A.80° B.70° C.60° D.50°
4.(3分)若式子中的x、y都扩大2倍,则分式的值( )
A.不变 B.扩大2倍 C.扩大4倍 D.缩小2倍
5.(3分)如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB、AC于点D、E.若AB=5,AC=4,则△ADE的周长是( )
A.9 B.10 C.12 D.14
6.(3分)若方程=有增根,则a的值为( )
A.﹣1 B.1 C.2 D.﹣2
7.(3分)分式﹣可变形为( )
A.﹣ B. C.﹣ D.
8.(3分)货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是( )
A. B. C. D.
9.(3分)已知,则的值是( )
A.28 B.30 C.32 D.34
10.(3分)如图,在△ABC中,DE是AC的垂直平分线,AE=4cm,且△ABD的周长为16cm,则△ABC的周长为( )
A.24cm B.22cm C.20cm D.18cm
二、填空题(每小题3分,共24分)
11.(3分)科学家测得新冠病毒的直径约为0.0000103cm,用科学记数法表示为 .
12.(3分)如图,在△ABC中,D、E分别是AB,AC上面的点,若已知∠1=∠2,BE=CD,AB=9,AE=2,则CE= .
13.(3分)若2x=2,4y=4,则2x﹣2y的值为 .
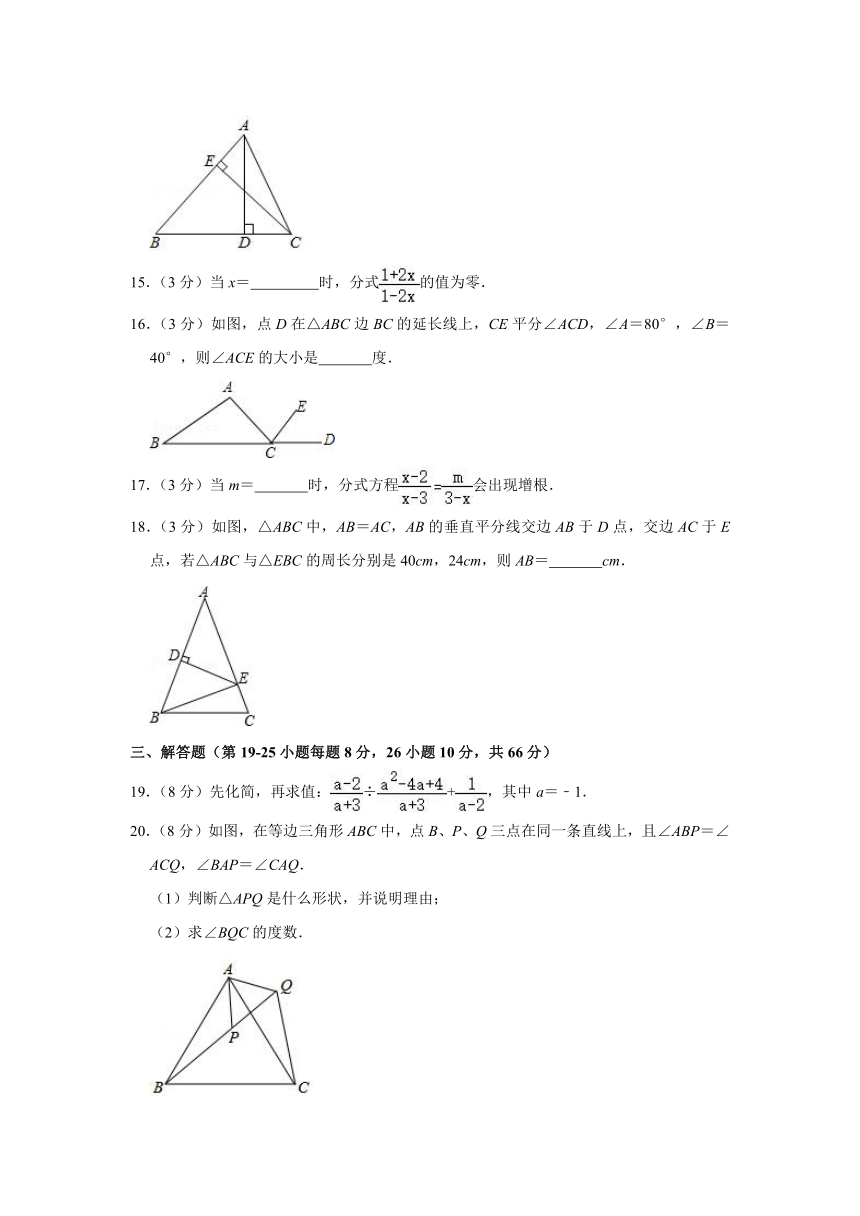
14.(3分)如图,AD,CE是△ABC的两条高,已知AD=5,CE=4,AB=8,则BC的长是 .
15.(3分)当x= 时,分式的值为零.
16.(3分)如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是 度.
17.(3分)当m= 时,分式方程会出现增根.
18.(3分)如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB= cm.
三、解答题(第19-25小题每题8分,26小题10分,共66分)
19.(8分)先化简,再求值:÷+,其中a=﹣1.
20.(8分)如图,在等边三角形ABC中,点B、P、Q三点在同一条直线上,且∠ABP=∠ACQ,∠BAP=∠CAQ.
(1)判断△APQ是什么形状,并说明理由;
(2)求∠BQC的度数.
21.(8分)解方程:
(1)=;
(2)+=3.
22.(8分)如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且AE=AB.
(1)若∠BAE=40°,求∠C的度数;
(2)若△ABC周长26cm,AC=10cm,求DC长.
23.(8分)已知==,求的值.
24.(8分)如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:
(1)FC=AD;
(2)AB=BC+AD.
25.(8分)今年新冠疫情期间,某公司计划将1200套新型防护服进行加工,分给甲乙两个工厂,甲工厂单独完成任务,比乙工厂单独完成任务多用10天,乙工厂每天加工数量是甲的1.5倍,甲工厂每天费用200元,乙工厂每天费用350元.
(1)求甲乙两个工厂每天分别能加工多少套?
(2)从经济角度考虑,选用哪个工厂较好?
26.(10分)如图,BE、CF分别是△ABC的边AC、AB上的高,且BP=AC,CQ=AB.求证:
(1)AP=AQ;
(2)AP⊥AQ.
2021-2022学年湖南省邵阳市邵阳县八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.(3分)下列式子:,,,3x+,中,是分式的有( )
A.2个 B.3个 C.4个 D.5个
【分析】判断分式的依据是看代数式的分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式,然后找出分式的个数.
【解答】解:,3x+,的分母中含有字母,属于分式,共有3个.
故选:B.
2.(3分)如图,AB∥DE,AF=DC,若要证明△ABC≌△DEF,还需补充的条件是( )
A.AC=DF B.AB=DE C.∠A=∠D D.BC=EF
【分析】根据平行线的性质得出∠A=∠D,求出AC=DF,根据全等三角形的判定定理逐个判断即可.
【解答】解:AB=DE,
理由是:∵AB∥DE,
∴∠A=∠D,
∵AF=DC,
∴AF+FC=DC+FC,
∴AC=DF,
在△ABC和△DEF中
∴△ABC≌△DEF(SAS),即选项B正确,
选项A、C、D都不能推出△ABC≌△DEF,即选项A、C、D都错误,
故选:B.
3.(3分)如图,△ABC≌△BAD,点A和点B,点C和点D是对应点.如果∠D=70°,∠CAB=50°,那么∠DAB度数是( )
A.80° B.70° C.60° D.50°
【分析】根据全等三角形的性质得到∠DBA=∠CAB=50°,根据三角形内角和定理计算即可.
【解答】解:△ABC≌△BAD,点A和点B,点C和点D是对应点,
∴∠DBA=∠CAB=50°,
∴∠DAB=180°﹣70°﹣50°=60°,
故选:C.
4.(3分)若式子中的x、y都扩大2倍,则分式的值( )
A.不变 B.扩大2倍 C.扩大4倍 D.缩小2倍
【分析】先根据题意列出算式,再根据分式的基本性质进行化简即可.
【解答】解:===,
所以式子中的x、y都扩大2倍,那么分式的值扩大2倍,
故选:B.
5.(3分)如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB、AC于点D、E.若AB=5,AC=4,则△ADE的周长是( )
A.9 B.10 C.12 D.14
【分析】先由角平分线的定义得∠DBF=∠CBF,∠ECF=∠BCF,再由平行线的性质得∠DFB=∠CBF,∠BCF=∠EFC,则∠DBF=∠DFB,∠ECF=∠EFC,得DB=DF,EF=EC,即可解决问题.
【解答】解:∵∠ABC和∠ACB的平分线相交于点F,
∴∠DBF=∠CBF,∠ECF=∠BCF,
∵DE∥BC,
∴∠DFB=∠CBF,∠BCF=∠EFC,
∴∠DBF=∠DFB,∠ECF=∠EFC,
∴DB=DF,EF=EC,
∴△ADE的周长=AD+DE+AE
=AD+DF+EF+AE
=AD+BD+EC+AE
=AB+AC
=5+4
=9.
故选:A.
6.(3分)若方程=有增根,则a的值为( )
A.﹣1 B.1 C.2 D.﹣2
【分析】分式方程去分母转化为整式方程,由分式方程有增根求出x的值,代入整式方程计算即可求出a的值.
【解答】解:去分母得:x﹣1=a,
由分式方程有增根,得到x﹣2=0,即x=2,
代入整式方程得:a=1,
故选:B.
7.(3分)分式﹣可变形为( )
A.﹣ B. C.﹣ D.
【分析】根据分式的基本性质进行解答即可.
【解答】解:由分式的基本性质,把分式的分子和分母同时乘以﹣1得,(﹣1)×(﹣)=.
故选:D.
8.(3分)货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是( )
A. B. C. D.
【分析】题中等量关系:货车行驶25千米与小车行驶35千米所用时间相同,列出关系式.
【解答】解:根据题意,得
.
故选:C.
9.(3分)已知,则的值是( )
A.28 B.30 C.32 D.34
【分析】将代入=(x﹣)2﹣4计算可得答案.
【解答】解:∵,
∴
=(x﹣)2﹣4
=62﹣4
=36﹣4
=32.
故选:C.
10.(3分)如图,在△ABC中,DE是AC的垂直平分线,AE=4cm,且△ABD的周长为16cm,则△ABC的周长为( )
A.24cm B.22cm C.20cm D.18cm
【分析】根据线段垂直平分线的性质得到AC=2AE=8cm,AD=DC,求得AB+BD+AD=AB+BD+CD=AB+BC=16cm,于是得到结论.
【解答】解:∵DE是AC的垂直平分线,AE=4cm,
∴AC=2AE=8cm,AD=DC,
∵△ABD的周长为16cm,
∴AB+BD+AD=AB+BD+CD=AB+BC=16(cm),
∴△ABC的周长为AB+BC+AC=16+8=24(cm),
故选:A.
二、填空题(每小题3分,共24分)
11.(3分)科学家测得新冠病毒的直径约为0.0000103cm,用科学记数法表示为 1.03×10﹣5cm .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
【解答】解:0.0000103cm用科学记数法表示为1.03×10﹣5cm.
故答案为:1.03×10﹣5cm.
12.(3分)如图,在△ABC中,D、E分别是AB,AC上面的点,若已知∠1=∠2,BE=CD,AB=9,AE=2,则CE= 7 .
【分析】根据AAS即可证明△ABE≌△ACD,根据该全等三角形的对应边相等证得结论.
【解答】(1)证明:在△ABE和△ACD中,
,
∴△ABE≌△ACD(AAS).
∴AB=AC=9,AE=AD=2,
∴CE=AC﹣AE=9﹣2=7.
故答案为:7.
13.(3分)若2x=2,4y=4,则2x﹣2y的值为 .
【分析】根据幂的乘方运算法则可得4y=22y=4,再根据同底数幂的除法法则计算即可,
【解答】解:∵2x=2,4y=22y=4,
∴2x﹣2y=2x÷22y=2÷4=.
故答案为:.
14.(3分)如图,AD,CE是△ABC的两条高,已知AD=5,CE=4,AB=8,则BC的长是 6.4 .
【分析】利用三角形的面积可得CB AD=AB CE,再代入数据即可.
【解答】解:∵AD,CE是△ABC的两条高,
∴S△ACB=CB AD=AB CE,
∵AD=5,CE=4,AB=8,
∴×BC×5=,
解得:BC=6.4,
故答案为:6.4.
15.(3分)当x= ﹣0.5 时,分式的值为零.
【分析】分式的值为0的条件是:(1)分子=0;(2)分母≠0.两个条件需同时具备,缺一不可.据此可以解答本题.
【解答】解:分式的值为零,则1+2x=0,解得x=﹣0.5.
又∵1﹣2x≠0,解得x≠0.5.
∴x=﹣0.5.
故答案为﹣0.5.
16.(3分)如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是 60 度.
【分析】由∠A=80°,∠B=40°,根据三角形任意一个外角等于与之不相邻的两内角的和得到∠ACD=∠B+∠A,然后利用角平分线的定义计算即可.
【解答】解:∵∠ACD=∠B+∠A,
而∠A=80°,∠B=40°,
∴∠ACD=80°+40°=120°.
∵CE平分∠ACD,
∴∠ACE=60°,
故答案为60
17.(3分)当m= ﹣1 时,分式方程会出现增根.
【分析】分式方程去分母转化为整式方程,由分式方程有增根确定出x的值,代入整式方程计算即可求出m的值.
【解答】解:分式方程去分母得:x﹣2=﹣m,
由分式方程有增根,得到x﹣3=0,即x=3,
把x=3代入整式方程得:m=﹣1.
故答案为:﹣1.
18.(3分)如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB= 16 cm.
【分析】首先根据DE是AB的垂直平分线,可得AE=BE;然后根据△ABC的周长=AB+AC+BC,△EBC的周长=BE+EC+BC=AE+EC+BC=AC+BC,可得△ABC的周长﹣△EBC的周长=AB,据此求出AB的长度是多少即可.
【解答】解:∵DE是AB的垂直平分线,
∴AE=BE;
∵△ABC的周长=AB+AC+BC,△EBC的周长=BE+EC+BC=AE+EC+BC=AC+BC,
∴△ABC的周长﹣△EBC的周长=AB,
∴AB=40﹣24=16(cm).
故答案为:16.
三、解答题(第19-25小题每题8分,26小题10分,共66分)
19.(8分)先化简,再求值:÷+,其中a=﹣1.
【分析】原式第一项利用除法法则变形,约分后两项通分并利用同分母分式的加法法则计算得到最简结果,把a的值代入计算即可求出值.
【解答】解:原式= +
=+
=,
当a=﹣1时,原式==﹣.
20.(8分)如图,在等边三角形ABC中,点B、P、Q三点在同一条直线上,且∠ABP=∠ACQ,∠BAP=∠CAQ.
(1)判断△APQ是什么形状,并说明理由;
(2)求∠BQC的度数.
【分析】(1)根据等边三角形的性质得到AB=AC,∠BAC=60°,根据全等三角形的性质得到AP=AQ,根据等边三角形的判定定理得到△PAQ是等边三角形;
(2)如图,设BQ,AC交于O,根据对顶角的性质和三角形的内角和定理即可得到结论.
【解答】解:(1)△APQ是等边三角形,
理由:∵△ACB是等边三角形,
∴AB=AC,∠BAC=60°,
在△ABP与△ACQ中,
,
∴△ABP≌△ACQ(ASA),
∴AP=AQ,
∵∠BAP+∠PAC=∠PAC+∠CAQ,
即∠BAC=∠PAQ=60°,
∴△PAQ是等边三角形;
(2)如图,设BQ,AC交于O,
∵∠ABP=∠ACQ,∠AOB=∠QOC,
∴∠BAC=∠BQC=60°.
21.(8分)解方程:
(1)=;
(2)+=3.
【分析】(1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【解答】解:(1)去分母得:x+3=4x,
解得:x=1,
检验:把x=1代入得:x(x+3)≠0,
∴分式方程的解为x=1;
(2)去分母得:x﹣2=3x﹣3,
解得:x=,
检验:把x=代入得:x﹣1≠0,
∴分式方程的解为x=.
22.(8分)如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且AE=AB.
(1)若∠BAE=40°,求∠C的度数;
(2)若△ABC周长26cm,AC=10cm,求DC长.
【分析】(1)根据线段垂直平分线和等腰三角形性质得出AB=AE=CE,求出∠AEB和∠C=∠EAC,即可得出答案;
(2)根据已知能推出2DE+2EC=10cm,即可得出答案.
【解答】解:(1)∵AD⊥BC,AE=AB,EF垂直平分AC,
∴AB=AE=EC,
∴∠C=∠CAE,
∵∠BAE=40°,
∴∠AED=×(180°﹣40°)=70°,
∴∠C=∠AED=35°;
(2)∵△ABC周长26cm,AC=10cm,
∴AB+BC=16(cm),
∴AB+BE+EC=16(cm),
即2DE+2EC=16(cm),
∴DE+EC=8(cm),
∴DC=DE+EC=8(cm).
23.(8分)已知==,求的值.
【分析】设===k,根据比例的性质知x=3k,y=4k,z=5k.将它们代入所求的代数式,通过约分求值.
【解答】解:∵当x=y=z时,分式无意义,
∴x、y、z均不为0,
∴设===k(k≠0),则x=3k,y=4k,z=5k.
所以,==,即的值是.
24.(8分)如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:
(1)FC=AD;
(2)AB=BC+AD.
【分析】(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)根据线段垂直平分线的性质判断出AB=BF即可.
【解答】证明:(1)∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
∵在△ADE与△FCE中,
,
∴△ADE≌△FCE(ASA),
∴FC=AD(全等三角形的性质).
(2)∵△ADE≌△FCE,
∴AE=EF,AD=CF(全等三角形的对应边相等),
又∵BE⊥AF,
∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF,
∵AD=CF(已证),
∴AB=BC+AD(等量代换).
25.(8分)今年新冠疫情期间,某公司计划将1200套新型防护服进行加工,分给甲乙两个工厂,甲工厂单独完成任务,比乙工厂单独完成任务多用10天,乙工厂每天加工数量是甲的1.5倍,甲工厂每天费用200元,乙工厂每天费用350元.
(1)求甲乙两个工厂每天分别能加工多少套?
(2)从经济角度考虑,选用哪个工厂较好?
【分析】(1)设甲工厂每天能加工x套新型防护服,则乙工厂每天能加工1.5x套新型防护服,根据工作时间=工作总量÷工作效率结合甲工厂单独完成任务比乙工厂单独完成任务多用10天,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)利用总费用=每天需要的费用×工作时间,可分别求出选择甲、乙两工厂所需费用,比较后即可得出结论.
【解答】解:(1)设甲工厂每天能加工x套新型防护服,则乙工厂每天能加工1.5x套新型防护服,
依题意得:﹣=10,
解得:x=40,
经检验,x=40是原方程的解且符合题意,
∴1.5x=60.
答:甲工厂每天能加工40套新型防护服,乙工厂每天能加工60套新型防护服.
(2)选择甲工厂所需费用为200×=6000(元);
选择乙工厂所需费用为350×=7000(元).
∵6000<7000,
∴从经济角度考虑,选用甲工厂较好.
26.(10分)如图,BE、CF分别是△ABC的边AC、AB上的高,且BP=AC,CQ=AB.求证:
(1)AP=AQ;
(2)AP⊥AQ.
【分析】(1)首先证明∠FCA=∠ABP,再加上条件BP=AC,CQ=AB可以证明△QAC≌△APB进而得到AP=AQ;
(2)根据△QAC≌△APB可得∠AQF=∠PAF,再证明∠FQA+∠FAQ=90°可得∠FQA+∠PAF=90°,进而得到∠PAQ=90°,即可证出AP⊥AQ.
【解答】证明:(1)∵AC⊥BE,AB⊥QC,
∴∠BFP=∠CEP=90°,
∴∠BAC+∠FCA=90°,∠ABP+∠BAC=90°
∴∠FCA=∠ABP,
在△QAC和△APB中,,
∴△QAC≌△APB(SAS),
∴AP=AQ;
(2)∵△QAC≌△APB,
∴∠AQF=∠PAF,
又AB⊥QC,
∴∠QFA=90°,
∴∠FQA+∠FAQ=90°,
∴∠FQA+∠PAF=90°,
即∠PAQ=90°,
∴AP⊥AQ.
一、选择题(每小题3分,共30分)
1.(3分)下列式子:,,,3x+,中,是分式的有( )
A.2个 B.3个 C.4个 D.5个
2.(3分)如图,AB∥DE,AF=DC,若要证明△ABC≌△DEF,还需补充的条件是( )
A.AC=DF B.AB=DE C.∠A=∠D D.BC=EF
3.(3分)如图,△ABC≌△BAD,点A和点B,点C和点D是对应点.如果∠D=70°,∠CAB=50°,那么∠DAB度数是( )
A.80° B.70° C.60° D.50°
4.(3分)若式子中的x、y都扩大2倍,则分式的值( )
A.不变 B.扩大2倍 C.扩大4倍 D.缩小2倍
5.(3分)如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB、AC于点D、E.若AB=5,AC=4,则△ADE的周长是( )
A.9 B.10 C.12 D.14
6.(3分)若方程=有增根,则a的值为( )
A.﹣1 B.1 C.2 D.﹣2
7.(3分)分式﹣可变形为( )
A.﹣ B. C.﹣ D.
8.(3分)货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是( )
A. B. C. D.
9.(3分)已知,则的值是( )
A.28 B.30 C.32 D.34
10.(3分)如图,在△ABC中,DE是AC的垂直平分线,AE=4cm,且△ABD的周长为16cm,则△ABC的周长为( )
A.24cm B.22cm C.20cm D.18cm
二、填空题(每小题3分,共24分)
11.(3分)科学家测得新冠病毒的直径约为0.0000103cm,用科学记数法表示为 .
12.(3分)如图,在△ABC中,D、E分别是AB,AC上面的点,若已知∠1=∠2,BE=CD,AB=9,AE=2,则CE= .
13.(3分)若2x=2,4y=4,则2x﹣2y的值为 .
14.(3分)如图,AD,CE是△ABC的两条高,已知AD=5,CE=4,AB=8,则BC的长是 .
15.(3分)当x= 时,分式的值为零.
16.(3分)如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是 度.
17.(3分)当m= 时,分式方程会出现增根.
18.(3分)如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB= cm.
三、解答题(第19-25小题每题8分,26小题10分,共66分)
19.(8分)先化简,再求值:÷+,其中a=﹣1.
20.(8分)如图,在等边三角形ABC中,点B、P、Q三点在同一条直线上,且∠ABP=∠ACQ,∠BAP=∠CAQ.
(1)判断△APQ是什么形状,并说明理由;
(2)求∠BQC的度数.
21.(8分)解方程:
(1)=;
(2)+=3.
22.(8分)如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且AE=AB.
(1)若∠BAE=40°,求∠C的度数;
(2)若△ABC周长26cm,AC=10cm,求DC长.
23.(8分)已知==,求的值.
24.(8分)如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:
(1)FC=AD;
(2)AB=BC+AD.
25.(8分)今年新冠疫情期间,某公司计划将1200套新型防护服进行加工,分给甲乙两个工厂,甲工厂单独完成任务,比乙工厂单独完成任务多用10天,乙工厂每天加工数量是甲的1.5倍,甲工厂每天费用200元,乙工厂每天费用350元.
(1)求甲乙两个工厂每天分别能加工多少套?
(2)从经济角度考虑,选用哪个工厂较好?
26.(10分)如图,BE、CF分别是△ABC的边AC、AB上的高,且BP=AC,CQ=AB.求证:
(1)AP=AQ;
(2)AP⊥AQ.
2021-2022学年湖南省邵阳市邵阳县八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.(3分)下列式子:,,,3x+,中,是分式的有( )
A.2个 B.3个 C.4个 D.5个
【分析】判断分式的依据是看代数式的分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式,然后找出分式的个数.
【解答】解:,3x+,的分母中含有字母,属于分式,共有3个.
故选:B.
2.(3分)如图,AB∥DE,AF=DC,若要证明△ABC≌△DEF,还需补充的条件是( )
A.AC=DF B.AB=DE C.∠A=∠D D.BC=EF
【分析】根据平行线的性质得出∠A=∠D,求出AC=DF,根据全等三角形的判定定理逐个判断即可.
【解答】解:AB=DE,
理由是:∵AB∥DE,
∴∠A=∠D,
∵AF=DC,
∴AF+FC=DC+FC,
∴AC=DF,
在△ABC和△DEF中
∴△ABC≌△DEF(SAS),即选项B正确,
选项A、C、D都不能推出△ABC≌△DEF,即选项A、C、D都错误,
故选:B.
3.(3分)如图,△ABC≌△BAD,点A和点B,点C和点D是对应点.如果∠D=70°,∠CAB=50°,那么∠DAB度数是( )
A.80° B.70° C.60° D.50°
【分析】根据全等三角形的性质得到∠DBA=∠CAB=50°,根据三角形内角和定理计算即可.
【解答】解:△ABC≌△BAD,点A和点B,点C和点D是对应点,
∴∠DBA=∠CAB=50°,
∴∠DAB=180°﹣70°﹣50°=60°,
故选:C.
4.(3分)若式子中的x、y都扩大2倍,则分式的值( )
A.不变 B.扩大2倍 C.扩大4倍 D.缩小2倍
【分析】先根据题意列出算式,再根据分式的基本性质进行化简即可.
【解答】解:===,
所以式子中的x、y都扩大2倍,那么分式的值扩大2倍,
故选:B.
5.(3分)如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB、AC于点D、E.若AB=5,AC=4,则△ADE的周长是( )
A.9 B.10 C.12 D.14
【分析】先由角平分线的定义得∠DBF=∠CBF,∠ECF=∠BCF,再由平行线的性质得∠DFB=∠CBF,∠BCF=∠EFC,则∠DBF=∠DFB,∠ECF=∠EFC,得DB=DF,EF=EC,即可解决问题.
【解答】解:∵∠ABC和∠ACB的平分线相交于点F,
∴∠DBF=∠CBF,∠ECF=∠BCF,
∵DE∥BC,
∴∠DFB=∠CBF,∠BCF=∠EFC,
∴∠DBF=∠DFB,∠ECF=∠EFC,
∴DB=DF,EF=EC,
∴△ADE的周长=AD+DE+AE
=AD+DF+EF+AE
=AD+BD+EC+AE
=AB+AC
=5+4
=9.
故选:A.
6.(3分)若方程=有增根,则a的值为( )
A.﹣1 B.1 C.2 D.﹣2
【分析】分式方程去分母转化为整式方程,由分式方程有增根求出x的值,代入整式方程计算即可求出a的值.
【解答】解:去分母得:x﹣1=a,
由分式方程有增根,得到x﹣2=0,即x=2,
代入整式方程得:a=1,
故选:B.
7.(3分)分式﹣可变形为( )
A.﹣ B. C.﹣ D.
【分析】根据分式的基本性质进行解答即可.
【解答】解:由分式的基本性质,把分式的分子和分母同时乘以﹣1得,(﹣1)×(﹣)=.
故选:D.
8.(3分)货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是( )
A. B. C. D.
【分析】题中等量关系:货车行驶25千米与小车行驶35千米所用时间相同,列出关系式.
【解答】解:根据题意,得
.
故选:C.
9.(3分)已知,则的值是( )
A.28 B.30 C.32 D.34
【分析】将代入=(x﹣)2﹣4计算可得答案.
【解答】解:∵,
∴
=(x﹣)2﹣4
=62﹣4
=36﹣4
=32.
故选:C.
10.(3分)如图,在△ABC中,DE是AC的垂直平分线,AE=4cm,且△ABD的周长为16cm,则△ABC的周长为( )
A.24cm B.22cm C.20cm D.18cm
【分析】根据线段垂直平分线的性质得到AC=2AE=8cm,AD=DC,求得AB+BD+AD=AB+BD+CD=AB+BC=16cm,于是得到结论.
【解答】解:∵DE是AC的垂直平分线,AE=4cm,
∴AC=2AE=8cm,AD=DC,
∵△ABD的周长为16cm,
∴AB+BD+AD=AB+BD+CD=AB+BC=16(cm),
∴△ABC的周长为AB+BC+AC=16+8=24(cm),
故选:A.
二、填空题(每小题3分,共24分)
11.(3分)科学家测得新冠病毒的直径约为0.0000103cm,用科学记数法表示为 1.03×10﹣5cm .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
【解答】解:0.0000103cm用科学记数法表示为1.03×10﹣5cm.
故答案为:1.03×10﹣5cm.
12.(3分)如图,在△ABC中,D、E分别是AB,AC上面的点,若已知∠1=∠2,BE=CD,AB=9,AE=2,则CE= 7 .
【分析】根据AAS即可证明△ABE≌△ACD,根据该全等三角形的对应边相等证得结论.
【解答】(1)证明:在△ABE和△ACD中,
,
∴△ABE≌△ACD(AAS).
∴AB=AC=9,AE=AD=2,
∴CE=AC﹣AE=9﹣2=7.
故答案为:7.
13.(3分)若2x=2,4y=4,则2x﹣2y的值为 .
【分析】根据幂的乘方运算法则可得4y=22y=4,再根据同底数幂的除法法则计算即可,
【解答】解:∵2x=2,4y=22y=4,
∴2x﹣2y=2x÷22y=2÷4=.
故答案为:.
14.(3分)如图,AD,CE是△ABC的两条高,已知AD=5,CE=4,AB=8,则BC的长是 6.4 .
【分析】利用三角形的面积可得CB AD=AB CE,再代入数据即可.
【解答】解:∵AD,CE是△ABC的两条高,
∴S△ACB=CB AD=AB CE,
∵AD=5,CE=4,AB=8,
∴×BC×5=,
解得:BC=6.4,
故答案为:6.4.
15.(3分)当x= ﹣0.5 时,分式的值为零.
【分析】分式的值为0的条件是:(1)分子=0;(2)分母≠0.两个条件需同时具备,缺一不可.据此可以解答本题.
【解答】解:分式的值为零,则1+2x=0,解得x=﹣0.5.
又∵1﹣2x≠0,解得x≠0.5.
∴x=﹣0.5.
故答案为﹣0.5.
16.(3分)如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是 60 度.
【分析】由∠A=80°,∠B=40°,根据三角形任意一个外角等于与之不相邻的两内角的和得到∠ACD=∠B+∠A,然后利用角平分线的定义计算即可.
【解答】解:∵∠ACD=∠B+∠A,
而∠A=80°,∠B=40°,
∴∠ACD=80°+40°=120°.
∵CE平分∠ACD,
∴∠ACE=60°,
故答案为60
17.(3分)当m= ﹣1 时,分式方程会出现增根.
【分析】分式方程去分母转化为整式方程,由分式方程有增根确定出x的值,代入整式方程计算即可求出m的值.
【解答】解:分式方程去分母得:x﹣2=﹣m,
由分式方程有增根,得到x﹣3=0,即x=3,
把x=3代入整式方程得:m=﹣1.
故答案为:﹣1.
18.(3分)如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB= 16 cm.
【分析】首先根据DE是AB的垂直平分线,可得AE=BE;然后根据△ABC的周长=AB+AC+BC,△EBC的周长=BE+EC+BC=AE+EC+BC=AC+BC,可得△ABC的周长﹣△EBC的周长=AB,据此求出AB的长度是多少即可.
【解答】解:∵DE是AB的垂直平分线,
∴AE=BE;
∵△ABC的周长=AB+AC+BC,△EBC的周长=BE+EC+BC=AE+EC+BC=AC+BC,
∴△ABC的周长﹣△EBC的周长=AB,
∴AB=40﹣24=16(cm).
故答案为:16.
三、解答题(第19-25小题每题8分,26小题10分,共66分)
19.(8分)先化简,再求值:÷+,其中a=﹣1.
【分析】原式第一项利用除法法则变形,约分后两项通分并利用同分母分式的加法法则计算得到最简结果,把a的值代入计算即可求出值.
【解答】解:原式= +
=+
=,
当a=﹣1时,原式==﹣.
20.(8分)如图,在等边三角形ABC中,点B、P、Q三点在同一条直线上,且∠ABP=∠ACQ,∠BAP=∠CAQ.
(1)判断△APQ是什么形状,并说明理由;
(2)求∠BQC的度数.
【分析】(1)根据等边三角形的性质得到AB=AC,∠BAC=60°,根据全等三角形的性质得到AP=AQ,根据等边三角形的判定定理得到△PAQ是等边三角形;
(2)如图,设BQ,AC交于O,根据对顶角的性质和三角形的内角和定理即可得到结论.
【解答】解:(1)△APQ是等边三角形,
理由:∵△ACB是等边三角形,
∴AB=AC,∠BAC=60°,
在△ABP与△ACQ中,
,
∴△ABP≌△ACQ(ASA),
∴AP=AQ,
∵∠BAP+∠PAC=∠PAC+∠CAQ,
即∠BAC=∠PAQ=60°,
∴△PAQ是等边三角形;
(2)如图,设BQ,AC交于O,
∵∠ABP=∠ACQ,∠AOB=∠QOC,
∴∠BAC=∠BQC=60°.
21.(8分)解方程:
(1)=;
(2)+=3.
【分析】(1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【解答】解:(1)去分母得:x+3=4x,
解得:x=1,
检验:把x=1代入得:x(x+3)≠0,
∴分式方程的解为x=1;
(2)去分母得:x﹣2=3x﹣3,
解得:x=,
检验:把x=代入得:x﹣1≠0,
∴分式方程的解为x=.
22.(8分)如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且AE=AB.
(1)若∠BAE=40°,求∠C的度数;
(2)若△ABC周长26cm,AC=10cm,求DC长.
【分析】(1)根据线段垂直平分线和等腰三角形性质得出AB=AE=CE,求出∠AEB和∠C=∠EAC,即可得出答案;
(2)根据已知能推出2DE+2EC=10cm,即可得出答案.
【解答】解:(1)∵AD⊥BC,AE=AB,EF垂直平分AC,
∴AB=AE=EC,
∴∠C=∠CAE,
∵∠BAE=40°,
∴∠AED=×(180°﹣40°)=70°,
∴∠C=∠AED=35°;
(2)∵△ABC周长26cm,AC=10cm,
∴AB+BC=16(cm),
∴AB+BE+EC=16(cm),
即2DE+2EC=16(cm),
∴DE+EC=8(cm),
∴DC=DE+EC=8(cm).
23.(8分)已知==,求的值.
【分析】设===k,根据比例的性质知x=3k,y=4k,z=5k.将它们代入所求的代数式,通过约分求值.
【解答】解:∵当x=y=z时,分式无意义,
∴x、y、z均不为0,
∴设===k(k≠0),则x=3k,y=4k,z=5k.
所以,==,即的值是.
24.(8分)如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:
(1)FC=AD;
(2)AB=BC+AD.
【分析】(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)根据线段垂直平分线的性质判断出AB=BF即可.
【解答】证明:(1)∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
∵在△ADE与△FCE中,
,
∴△ADE≌△FCE(ASA),
∴FC=AD(全等三角形的性质).
(2)∵△ADE≌△FCE,
∴AE=EF,AD=CF(全等三角形的对应边相等),
又∵BE⊥AF,
∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF,
∵AD=CF(已证),
∴AB=BC+AD(等量代换).
25.(8分)今年新冠疫情期间,某公司计划将1200套新型防护服进行加工,分给甲乙两个工厂,甲工厂单独完成任务,比乙工厂单独完成任务多用10天,乙工厂每天加工数量是甲的1.5倍,甲工厂每天费用200元,乙工厂每天费用350元.
(1)求甲乙两个工厂每天分别能加工多少套?
(2)从经济角度考虑,选用哪个工厂较好?
【分析】(1)设甲工厂每天能加工x套新型防护服,则乙工厂每天能加工1.5x套新型防护服,根据工作时间=工作总量÷工作效率结合甲工厂单独完成任务比乙工厂单独完成任务多用10天,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)利用总费用=每天需要的费用×工作时间,可分别求出选择甲、乙两工厂所需费用,比较后即可得出结论.
【解答】解:(1)设甲工厂每天能加工x套新型防护服,则乙工厂每天能加工1.5x套新型防护服,
依题意得:﹣=10,
解得:x=40,
经检验,x=40是原方程的解且符合题意,
∴1.5x=60.
答:甲工厂每天能加工40套新型防护服,乙工厂每天能加工60套新型防护服.
(2)选择甲工厂所需费用为200×=6000(元);
选择乙工厂所需费用为350×=7000(元).
∵6000<7000,
∴从经济角度考虑,选用甲工厂较好.
26.(10分)如图,BE、CF分别是△ABC的边AC、AB上的高,且BP=AC,CQ=AB.求证:
(1)AP=AQ;
(2)AP⊥AQ.
【分析】(1)首先证明∠FCA=∠ABP,再加上条件BP=AC,CQ=AB可以证明△QAC≌△APB进而得到AP=AQ;
(2)根据△QAC≌△APB可得∠AQF=∠PAF,再证明∠FQA+∠FAQ=90°可得∠FQA+∠PAF=90°,进而得到∠PAQ=90°,即可证出AP⊥AQ.
【解答】证明:(1)∵AC⊥BE,AB⊥QC,
∴∠BFP=∠CEP=90°,
∴∠BAC+∠FCA=90°,∠ABP+∠BAC=90°
∴∠FCA=∠ABP,
在△QAC和△APB中,,
∴△QAC≌△APB(SAS),
∴AP=AQ;
(2)∵△QAC≌△APB,
∴∠AQF=∠PAF,
又AB⊥QC,
∴∠QFA=90°,
∴∠FQA+∠FAQ=90°,
∴∠FQA+∠PAF=90°,
即∠PAQ=90°,
∴AP⊥AQ.
同课章节目录
