沪科版数学七年级上册 4.3 线段的长短比较课件(共15张PPT)
文档属性
| 名称 | 沪科版数学七年级上册 4.3 线段的长短比较课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 126.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 20:50:56 | ||
图片预览




文档简介
(共15张PPT)
4.3 线段的长短比较
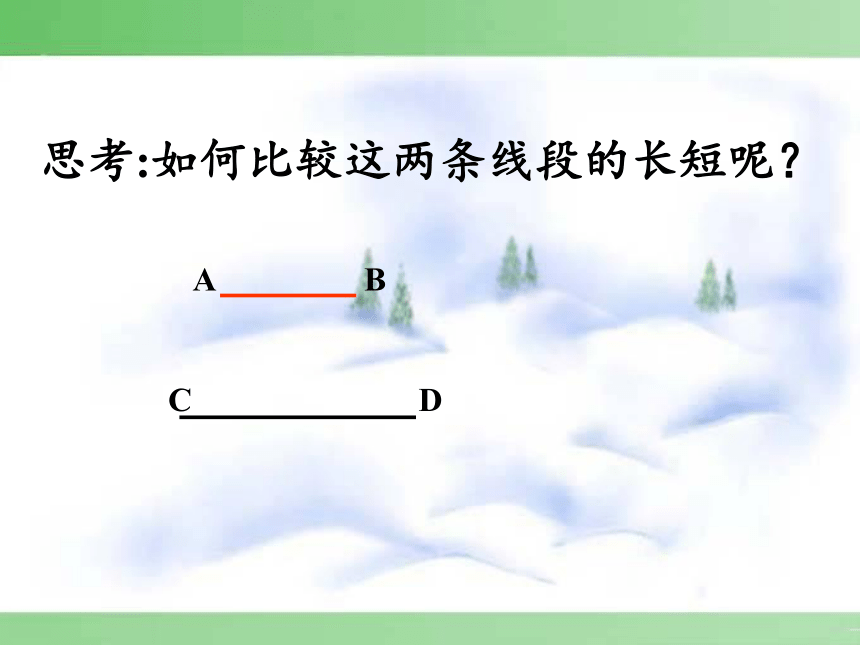
A
B
C
D
思考:如何比较这两条线段的长短呢?
线段的长短比较
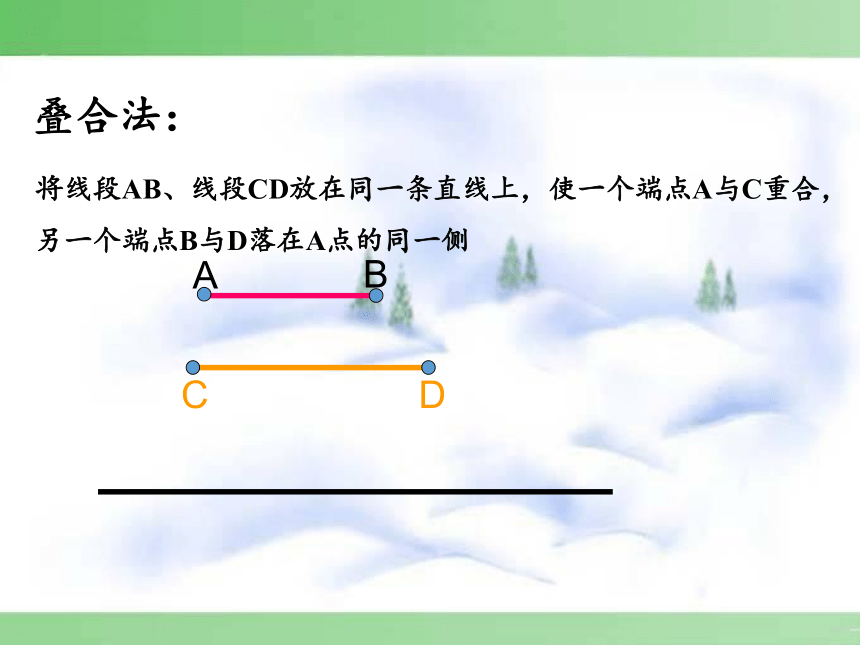
叠合法:
将线段AB、线段CD放在同一条直线上,使一个端点A与C重合,
另一个端点B与D落在A点的同一侧
C
D
A
B
A
B
D
C
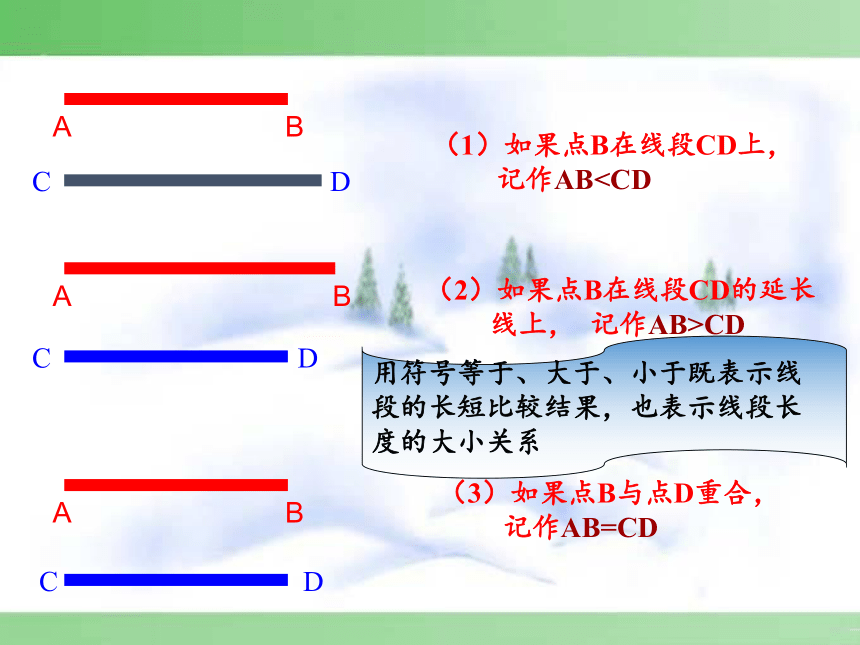
(1)如果点B在线段CD上,
记作ABA
B
D
C
(2)如果点B在线段CD的延长
线上, 记作AB>CD
(3)如果点B与点D重合,
记作AB=CD
A
B
C
D
用符号等于、大于、小于既表示线
段的长短比较结果,也表示线段长
度的大小关系
度量法:
利用刻度尺量出线段的长度,再比较两者数据的大小。
思考:除了叠合法外,是否还有别的方法?
练习:1
比较线段长短的两种方法:
1、度量法——从“数”的角度比较
2、叠合法——从“形”的角度比较
起点对齐,看终点
a
线段的和差
●
C
●
●
A
B
a
AB =a
b
BC=b
AC=AB+BC
=a+b
●
●
A
B
●
AB =a
D
b
DB=b
AD = AB-DB
= a - b
AC就是a与b的和
AD就是a与b的差
线段的和差表示的是线段长度的和差
练习:2
A
B
C
线段的中点:
∵ 点C是线段AB的中点
∴
或者AB=2AC=2CB
或者AB=2AC=2CB
∴ 点C是线段AB的中点
∵
点C在线段AB 上且使线段AC,CB相等,
这样的点C叫做线段AB的中点。
操作:你如何确定一条线段的中点
1、拿出一根无弹性的细绳子,让学生找到绳子的中点。
2、在一张白纸上画出一条线段,
请学生用折纸的方法找出线段的中点
3、用尺子度量
例题分析
如图,点C是线段AB上任意一点,点D是线段AC的中点,点E是线段BC的中点,则线段DE和线段AB有怎样的关系?说明理由.
.
.
A
B
.
C
.
.
D
E
解:
∵点D是线段AC的中点
∴ DC = AC
∵点E是线段BC的中点
∴ CE = BC
∴ DE
= DC + CE
= AC + BC
= (AC + BC)
= AB
DE = AB
理由如下:
已知:线段AB=4,延长AB至点C,使AC=11。
点D是AB的中点,点E是AC的中点。
求DE的长。
解 : ∵ AB=4,点D为AB的中点
∴ AD=2
●
●
●
●
●
A
D
B
E
C
又∵ AC=11,点E为AC中点,
∴ AE=5.5
∴ DE=AE-AD=5.5-2=3.5
练习:3
课堂小结
谈谈本节课你有哪些收获?
1、掌握了线段长短的两种比较方法
2、认识了线段的中点
3、学会了表示线段的和、差表示方法
作业布置
习题4.3 第2题
谢 谢
4.3 线段的长短比较
A
B
C
D
思考:如何比较这两条线段的长短呢?
线段的长短比较
叠合法:
将线段AB、线段CD放在同一条直线上,使一个端点A与C重合,
另一个端点B与D落在A点的同一侧
C
D
A
B
A
B
D
C
(1)如果点B在线段CD上,
记作AB
B
D
C
(2)如果点B在线段CD的延长
线上, 记作AB>CD
(3)如果点B与点D重合,
记作AB=CD
A
B
C
D
用符号等于、大于、小于既表示线
段的长短比较结果,也表示线段长
度的大小关系
度量法:
利用刻度尺量出线段的长度,再比较两者数据的大小。
思考:除了叠合法外,是否还有别的方法?
练习:1
比较线段长短的两种方法:
1、度量法——从“数”的角度比较
2、叠合法——从“形”的角度比较
起点对齐,看终点
a
线段的和差
●
C
●
●
A
B
a
AB =a
b
BC=b
AC=AB+BC
=a+b
●
●
A
B
●
AB =a
D
b
DB=b
AD = AB-DB
= a - b
AC就是a与b的和
AD就是a与b的差
线段的和差表示的是线段长度的和差
练习:2
A
B
C
线段的中点:
∵ 点C是线段AB的中点
∴
或者AB=2AC=2CB
或者AB=2AC=2CB
∴ 点C是线段AB的中点
∵
点C在线段AB 上且使线段AC,CB相等,
这样的点C叫做线段AB的中点。
操作:你如何确定一条线段的中点
1、拿出一根无弹性的细绳子,让学生找到绳子的中点。
2、在一张白纸上画出一条线段,
请学生用折纸的方法找出线段的中点
3、用尺子度量
例题分析
如图,点C是线段AB上任意一点,点D是线段AC的中点,点E是线段BC的中点,则线段DE和线段AB有怎样的关系?说明理由.
.
.
A
B
.
C
.
.
D
E
解:
∵点D是线段AC的中点
∴ DC = AC
∵点E是线段BC的中点
∴ CE = BC
∴ DE
= DC + CE
= AC + BC
= (AC + BC)
= AB
DE = AB
理由如下:
已知:线段AB=4,延长AB至点C,使AC=11。
点D是AB的中点,点E是AC的中点。
求DE的长。
解 : ∵ AB=4,点D为AB的中点
∴ AD=2
●
●
●
●
●
A
D
B
E
C
又∵ AC=11,点E为AC中点,
∴ AE=5.5
∴ DE=AE-AD=5.5-2=3.5
练习:3
课堂小结
谈谈本节课你有哪些收获?
1、掌握了线段长短的两种比较方法
2、认识了线段的中点
3、学会了表示线段的和、差表示方法
作业布置
习题4.3 第2题
谢 谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
