鲁教版(五四制)数学七年级上册 6.1 函数 课件(共20张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学七年级上册 6.1 函数 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 354.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
函数
Contents
目录
01
02
03
04
故事引入
新知探究
课堂小结
问题解决
05
随堂练习
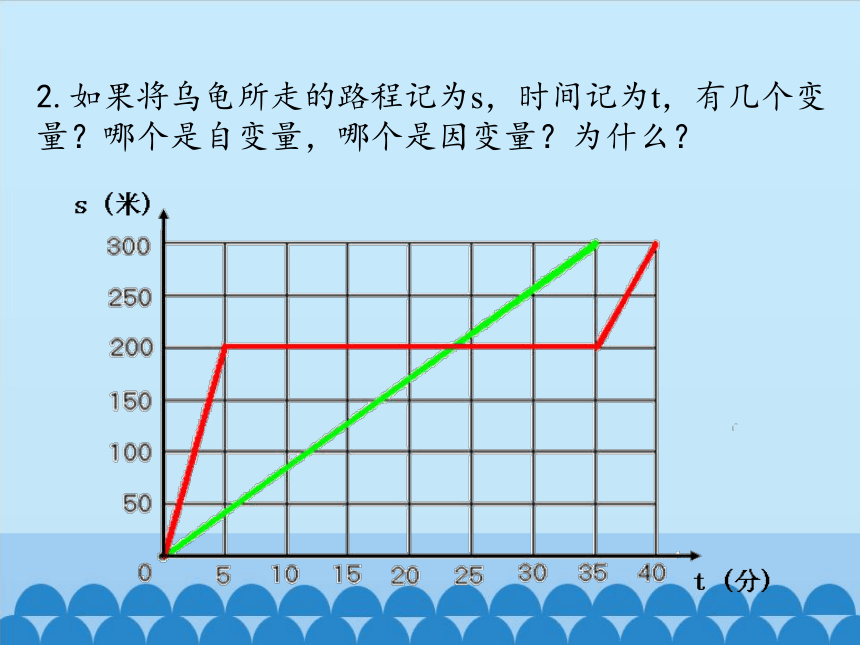
2.如果将乌龟所走的路程记为s,时间记为t,有几个变量?哪个是自变量,哪个是因变量?为什么?
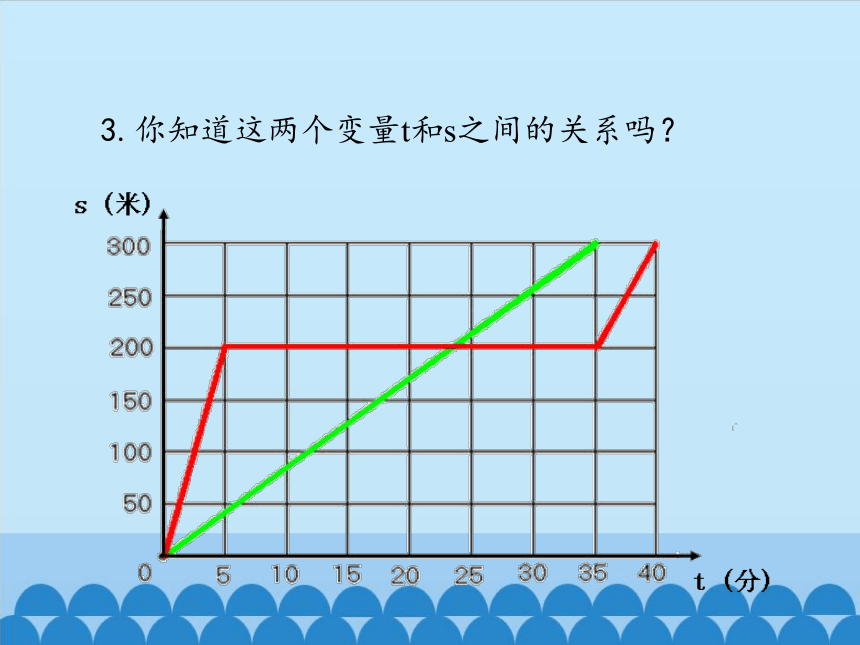
3.你知道这两个变量t和s之间的关系吗?
问题1:
你坐过摩天轮吗?
想一想,如果你坐在摩天轮上,随着时间的变化,你离开地面的高度是如何变化的?
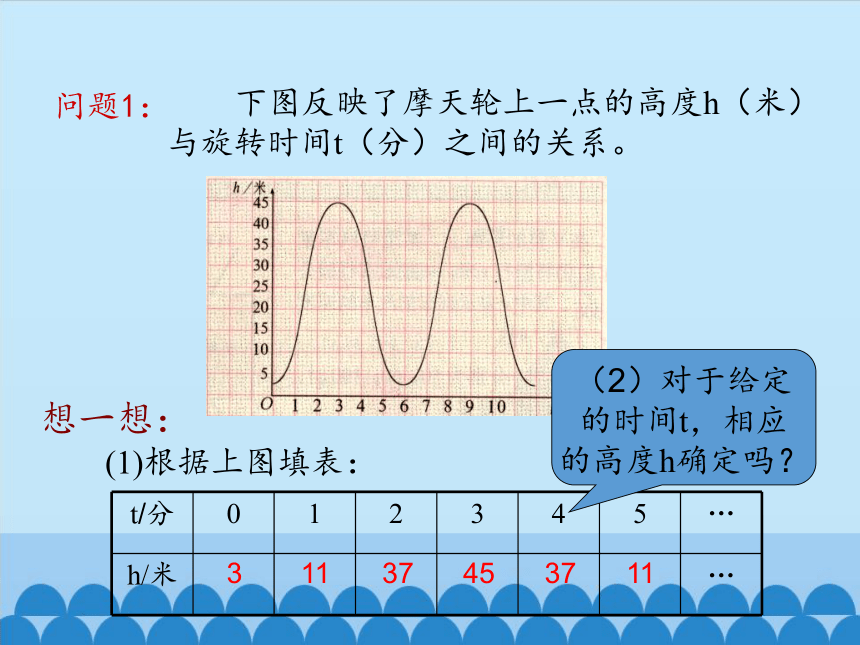
(1)根据上图填表:
t/分 0 1 2 3 4 5 …
h/米 …
3
45
37
11
11
37
(2)对于给定的时间t,相应的高度h确定吗?
想一想:
下图反映了摩天轮上一点的高度h(米)与旋转时间t(分)之间的关系。
问题1:
在该问题中,有两个变量t和h,其中:给定一个t(自变量)的值,相应的就确定了一个h(因变量)的值。
下图反映了摩天轮上一点的高度h(米)与旋转时间t(分)之间的关系。
问题1:
瓶子和罐头盒等圆柱形的物体,常常如下图那样堆放。随着层数的增加,物体的总数是如何变化的?
层数n 1 2 3 4 5 ···
物体总数y ···
1
3
6
10
15
1.
根据上图,填写下表:
对于给定的层数n,相应的物体总数y确定吗?
层数n 1 2 3 4 5 ···
物体总数y ···
1
3
6
10
15
在该问题中,有两个变量n和y,其中:给定一个n(自变量)的值,相应的就确定了一个y(因变量)的值。
瓶子和罐头盒等圆柱形的物体,常常如下图那样堆放。随着层数的增加,物体的总数是如何变化的?
2.
在上面的各例中,都有两个变量,给定其中一个变量(自变量)的值,相应地就确定了另一个变量(因变量)的值。
一般地,在某个变化过程中,有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量。
关键词:两个变量,一个x值对应唯一确定的一个y值。
下列各题中分别有几个变量?你能将其中某个变量看成另一个变量的函数吗?
(1)
速度v
距离s
在该问题中,有两个变量v和s,
其中:给定一个v(自变量)的值,相应的就确定了一个s(因变量)
的值。
(2)在平整的路面上,某型号汽车紧急刹车后仍将
滑行s米,一般地有经验公式 ,其中v表示刹车
前汽车的速度(单位:千米/时)。
想一想:
不同点:在第一个问题中,是以图象的形式表示两个变量之间的关系,第二个问题中是列表的形式以表示两个变量之间的关系,第三个问题是以关系式的形式表示两个变量之间的关系。
函数常用的三种表示方式:
(1)图象法;(2)列表法;(3)关系式法。
以上三个函数的表示方式有什么不同?
思考生活中的某个变化过程,看看其中
是否存在函数关系,并指出自变量的取值范围。
具体要求:
四人为一小组,交流各自的想法;由一人负责整理大家的想法并向全班同学展示,其它同学可以补充。
联系生活:
通过这节课的学习,你有什么收获?
1.知识内容:
2.学习流程:
3.思想与方法:
(1)函数的定义:一般地,在某个变化过程中,有两个变量x和y,如果对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量。
(2)函数的三种表示方式:图象法;列表法;关系式法。
三个实际
问题讨论
总结共性
定义函数
问题解决
深入理解
联系生活
体会应用
数形结合思想;用函数的观点认识现实世界。
课后作业:
1.课本习题6.1 知识技能1;
2.课下利用网络、书籍搜集关于函数的有关资料,在班内交流分享。
谢 谢
函数
Contents
目录
01
02
03
04
故事引入
新知探究
课堂小结
问题解决
05
随堂练习
2.如果将乌龟所走的路程记为s,时间记为t,有几个变量?哪个是自变量,哪个是因变量?为什么?
3.你知道这两个变量t和s之间的关系吗?
问题1:
你坐过摩天轮吗?
想一想,如果你坐在摩天轮上,随着时间的变化,你离开地面的高度是如何变化的?
(1)根据上图填表:
t/分 0 1 2 3 4 5 …
h/米 …
3
45
37
11
11
37
(2)对于给定的时间t,相应的高度h确定吗?
想一想:
下图反映了摩天轮上一点的高度h(米)与旋转时间t(分)之间的关系。
问题1:
在该问题中,有两个变量t和h,其中:给定一个t(自变量)的值,相应的就确定了一个h(因变量)的值。
下图反映了摩天轮上一点的高度h(米)与旋转时间t(分)之间的关系。
问题1:
瓶子和罐头盒等圆柱形的物体,常常如下图那样堆放。随着层数的增加,物体的总数是如何变化的?
层数n 1 2 3 4 5 ···
物体总数y ···
1
3
6
10
15
1.
根据上图,填写下表:
对于给定的层数n,相应的物体总数y确定吗?
层数n 1 2 3 4 5 ···
物体总数y ···
1
3
6
10
15
在该问题中,有两个变量n和y,其中:给定一个n(自变量)的值,相应的就确定了一个y(因变量)的值。
瓶子和罐头盒等圆柱形的物体,常常如下图那样堆放。随着层数的增加,物体的总数是如何变化的?
2.
在上面的各例中,都有两个变量,给定其中一个变量(自变量)的值,相应地就确定了另一个变量(因变量)的值。
一般地,在某个变化过程中,有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量。
关键词:两个变量,一个x值对应唯一确定的一个y值。
下列各题中分别有几个变量?你能将其中某个变量看成另一个变量的函数吗?
(1)
速度v
距离s
在该问题中,有两个变量v和s,
其中:给定一个v(自变量)的值,相应的就确定了一个s(因变量)
的值。
(2)在平整的路面上,某型号汽车紧急刹车后仍将
滑行s米,一般地有经验公式 ,其中v表示刹车
前汽车的速度(单位:千米/时)。
想一想:
不同点:在第一个问题中,是以图象的形式表示两个变量之间的关系,第二个问题中是列表的形式以表示两个变量之间的关系,第三个问题是以关系式的形式表示两个变量之间的关系。
函数常用的三种表示方式:
(1)图象法;(2)列表法;(3)关系式法。
以上三个函数的表示方式有什么不同?
思考生活中的某个变化过程,看看其中
是否存在函数关系,并指出自变量的取值范围。
具体要求:
四人为一小组,交流各自的想法;由一人负责整理大家的想法并向全班同学展示,其它同学可以补充。
联系生活:
通过这节课的学习,你有什么收获?
1.知识内容:
2.学习流程:
3.思想与方法:
(1)函数的定义:一般地,在某个变化过程中,有两个变量x和y,如果对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量。
(2)函数的三种表示方式:图象法;列表法;关系式法。
三个实际
问题讨论
总结共性
定义函数
问题解决
深入理解
联系生活
体会应用
数形结合思想;用函数的观点认识现实世界。
课后作业:
1.课本习题6.1 知识技能1;
2.课下利用网络、书籍搜集关于函数的有关资料,在班内交流分享。
谢 谢
