2021-2022学年苏科版数学七年级上册6.2.2 角 课件(共22张PPT)
文档属性
| 名称 | 2021-2022学年苏科版数学七年级上册6.2.2 角 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 15:44:42 | ||
图片预览





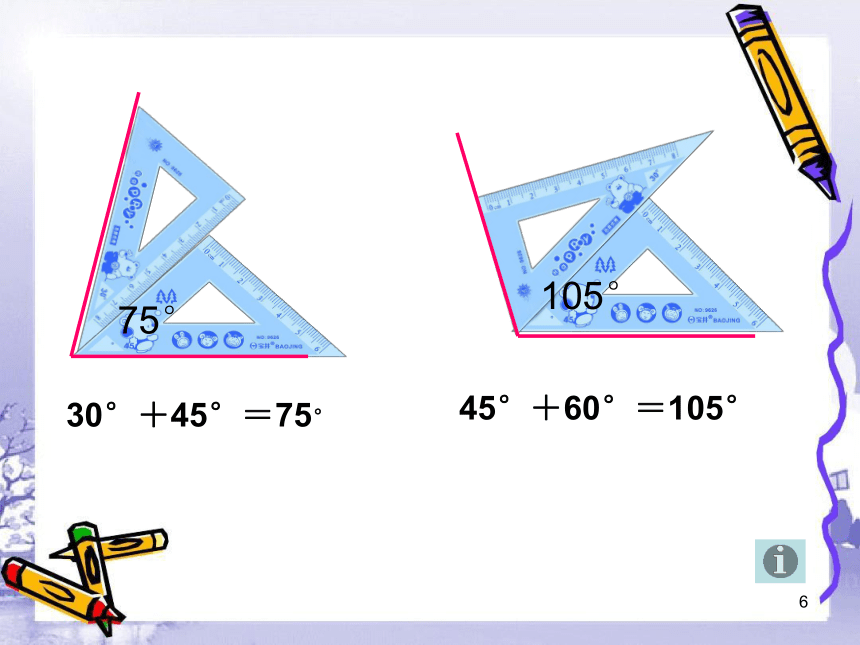

文档简介
(共22张PPT)
6.2 角(2)
*
复习巩固:
1、请叙述角的描述性定义。
2、角有哪几种表示方法?
3、角的单位有几种,它们之间是如何换算的?
*
学习目标
1.会用三角板﹑量角器﹑直尺和圆规画一个角
等于已知角;
2.在操作活动中理解角平分线的概念;
3.能够运用角平分线的知识,求简单的角的度数.
*
今天王小丫遇到一个非常头痛的问题:老师
让同学们画10个不同的角,要求精确标上度数.
王小丫打开文具盒一看,愣住了!量角器忘记带了,只带了一副三角板和一个圆规, 她能否完成今天的任务呢
王小丫的困惑
王小丫
怎么办呢?
没辙了吧!
张小毛
*
利用一副三角板,完成下列问题:
1.你能画出30°的角吗
2.你能画出75°和105°的角吗
3.你用一副三角板能画哪些度数的角呢
(0°~ 180°)
4.其它任意度数的角你又如何完成
活动1.三角板画特殊角
*
75°
105°
30°+45°=75°
45°+60°=105°
*
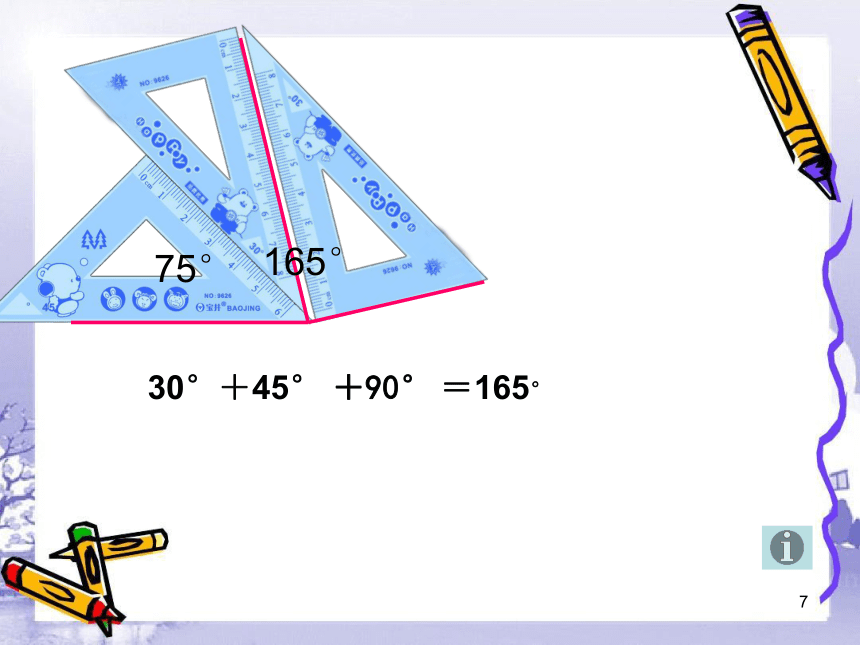
75°
30°+45° +90° =165°
165°
*
用一副三角板可以画出下列角
15°30°45°60° 75°90°105°
120°135° 150° 165°
想一想:这些度数有什么特征
凡是15倍数的角都能用一副三角板画出来.
结论:
*
O
A
B
活动2.量角器画角
量角器可以轻易地帮我们解决这个问题
画一个角等于已知∠AOB.
自己做学习的主人
*
O
A
B
画一个角等于已知∠AOB.
活动2.量角器画角
尺规作图
能否用圆规和直尺解决这个问题呢?
王小丫
*
尺规画角
O
A
B
O
A
你能行!
画一个角∠A O B 等于已知∠AOB.
*
(1)作图关键是__ 的确定.
(2)确定点D’至少需要__条弧线.
活动2.量角器画角
尺规作图
点
2
O
A
B
C
D
O
A
B
C
D
观察发现:点D在量角器的边缘弧上,
并且与点C的距离随着角的大小的确定而确定.
*
作 法 图 形
(2)作射线O′A′;
(1)以点O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D;
(3)以点O′为圆心,以OC长为半径画弧,交O′ A′于点C′;
(4)以点C′为圆心,以CD长为半径画弧,交前面的弧于点D ′ ;
(5)过点D ′作射线O ′ B ′ .
活动2.
尺规作图
*
活动2.量角器画角
尺规作图
O
A
B
O
A
B
所以∠ A ′ O ′ B ′就是所求作的角。
C
D
C
D
*
观察与思考
角的大小与角的两边画出的长短有关吗?
角的大小与角的两边画出的长短没有关系。
*
将你手中的角对折,使其两边重合,折痕把这个角分成的两部分是什么图形,你发现它们的大小有什么关系?
动手做一做
折痕与这个角的两边组成两个角
它们的大小相等 ∠_____=∠______
活动3. 折纸
∠ AOB的平分线
射线
AOC
BOC
*
如图:射线OC平分∠AOB
探究∠AOC, ∠BOC, ∠AOB大小有何特殊关系?
活动3. 折纸 角平分线的探究
射线OC平分∠ AOB
∠ =∠ = ∠ AOB
或∠ AOB=2∠ AOC =2∠______
因为
因为
所以
所以
AOC
BOC
BOC
*
新知运用
如图,如果∠AOD=70°,OC是∠ AOD内的一条射线,OB是∠AOC的平分线,∠AOB=20°.求∠AOC与∠COD的度数.
∠AOB
∠AOC
∠COD
解:因为OB是∠AOC的平分线
所以∠AOC=2 ∠AOB=2×20°=40°
∠COD= ∠AOD- ∠AOC= 70° - 40°=30 °
解题可要规范哟!
*
1.已知∠AOB=600,以O为顶点,OB为一边,画出∠BOC=300.
(1) 画出符合条件∠BOC.
(2)求∠AOC度数.
如图右,∠AOC =∠AOB+∠BOC=80 °
C
O
B
A
C
B
A
O
解:如图左,∠AOC =∠AOB-∠BOC=40 °
拓展延伸
所以∠AOC = 40 ° 或80 °
*
2. 如图,OB是∠AOC的平分线,
OE是∠COD的平分线,
A
C
B
O
E
D
(1)若∠AOC=50°, ∠COD=80°,
那么∠BOE是多少度?
(2)若∠AOD=130°, 那么∠BOE是多少度?
(3)若∠BOE=60°, 那么∠AOD是多少度?
(4) 由上可知: ∠BOE=_____∠AOD.
1
2
*
练一练
3.如图, ∠AOD= 80°,OC是∠AOD内的一条射线,OB是∠AOC平分线, ∠AOB= 30°.试求∠AOC、 ∠COD的度数。
A
B
C
D
O
*
完成情境中的问题。
总结本节课的收获:
课堂小结:
*
6.2 角(2)
*
复习巩固:
1、请叙述角的描述性定义。
2、角有哪几种表示方法?
3、角的单位有几种,它们之间是如何换算的?
*
学习目标
1.会用三角板﹑量角器﹑直尺和圆规画一个角
等于已知角;
2.在操作活动中理解角平分线的概念;
3.能够运用角平分线的知识,求简单的角的度数.
*
今天王小丫遇到一个非常头痛的问题:老师
让同学们画10个不同的角,要求精确标上度数.
王小丫打开文具盒一看,愣住了!量角器忘记带了,只带了一副三角板和一个圆规, 她能否完成今天的任务呢
王小丫的困惑
王小丫
怎么办呢?
没辙了吧!
张小毛
*
利用一副三角板,完成下列问题:
1.你能画出30°的角吗
2.你能画出75°和105°的角吗
3.你用一副三角板能画哪些度数的角呢
(0°~ 180°)
4.其它任意度数的角你又如何完成
活动1.三角板画特殊角
*
75°
105°
30°+45°=75°
45°+60°=105°
*
75°
30°+45° +90° =165°
165°
*
用一副三角板可以画出下列角
15°30°45°60° 75°90°105°
120°135° 150° 165°
想一想:这些度数有什么特征
凡是15倍数的角都能用一副三角板画出来.
结论:
*
O
A
B
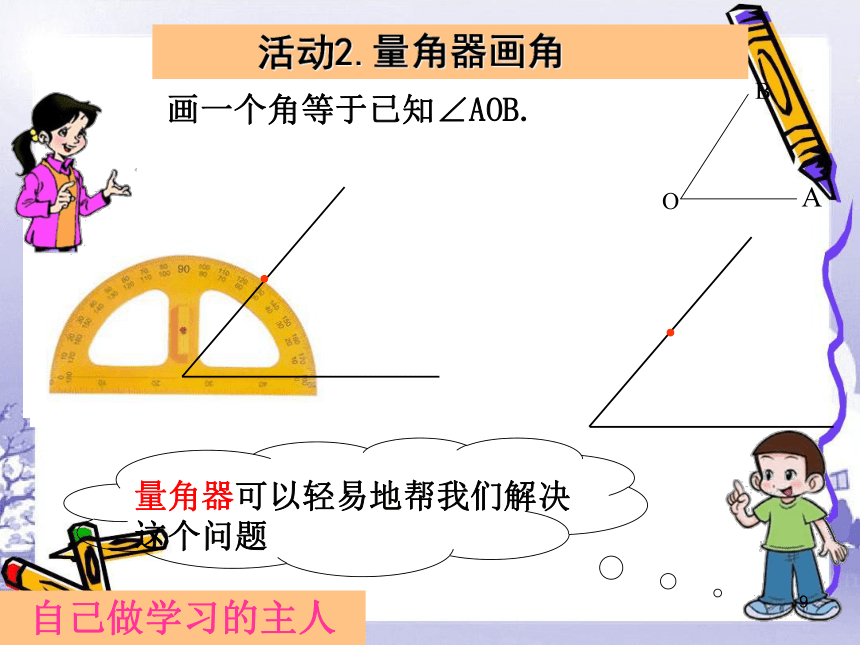
活动2.量角器画角
量角器可以轻易地帮我们解决这个问题
画一个角等于已知∠AOB.
自己做学习的主人
*
O
A
B
画一个角等于已知∠AOB.
活动2.量角器画角
尺规作图
能否用圆规和直尺解决这个问题呢?
王小丫
*
尺规画角
O
A
B
O
A
你能行!
画一个角∠A O B 等于已知∠AOB.
*
(1)作图关键是__ 的确定.
(2)确定点D’至少需要__条弧线.
活动2.量角器画角
尺规作图
点
2
O
A
B
C
D
O
A
B
C
D
观察发现:点D在量角器的边缘弧上,
并且与点C的距离随着角的大小的确定而确定.
*
作 法 图 形
(2)作射线O′A′;
(1)以点O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D;
(3)以点O′为圆心,以OC长为半径画弧,交O′ A′于点C′;
(4)以点C′为圆心,以CD长为半径画弧,交前面的弧于点D ′ ;
(5)过点D ′作射线O ′ B ′ .
活动2.
尺规作图
*
活动2.量角器画角
尺规作图
O
A
B
O
A
B
所以∠ A ′ O ′ B ′就是所求作的角。
C
D
C
D
*
观察与思考
角的大小与角的两边画出的长短有关吗?
角的大小与角的两边画出的长短没有关系。
*
将你手中的角对折,使其两边重合,折痕把这个角分成的两部分是什么图形,你发现它们的大小有什么关系?
动手做一做
折痕与这个角的两边组成两个角
它们的大小相等 ∠_____=∠______
活动3. 折纸
∠ AOB的平分线
射线
AOC
BOC
*
如图:射线OC平分∠AOB
探究∠AOC, ∠BOC, ∠AOB大小有何特殊关系?
活动3. 折纸 角平分线的探究
射线OC平分∠ AOB
∠ =∠ = ∠ AOB
或∠ AOB=2∠ AOC =2∠______
因为
因为
所以
所以
AOC
BOC
BOC
*
新知运用
如图,如果∠AOD=70°,OC是∠ AOD内的一条射线,OB是∠AOC的平分线,∠AOB=20°.求∠AOC与∠COD的度数.
∠AOB
∠AOC
∠COD
解:因为OB是∠AOC的平分线
所以∠AOC=2 ∠AOB=2×20°=40°
∠COD= ∠AOD- ∠AOC= 70° - 40°=30 °
解题可要规范哟!
*
1.已知∠AOB=600,以O为顶点,OB为一边,画出∠BOC=300.
(1) 画出符合条件∠BOC.
(2)求∠AOC度数.
如图右,∠AOC =∠AOB+∠BOC=80 °
C
O
B
A
C
B
A
O
解:如图左,∠AOC =∠AOB-∠BOC=40 °
拓展延伸
所以∠AOC = 40 ° 或80 °
*
2. 如图,OB是∠AOC的平分线,
OE是∠COD的平分线,
A
C
B
O
E
D
(1)若∠AOC=50°, ∠COD=80°,
那么∠BOE是多少度?
(2)若∠AOD=130°, 那么∠BOE是多少度?
(3)若∠BOE=60°, 那么∠AOD是多少度?
(4) 由上可知: ∠BOE=_____∠AOD.
1
2
*
练一练
3.如图, ∠AOD= 80°,OC是∠AOD内的一条射线,OB是∠AOC平分线, ∠AOB= 30°.试求∠AOC、 ∠COD的度数。
A
B
C
D
O
*
完成情境中的问题。
总结本节课的收获:
课堂小结:
*
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
