2021-2022学年北师大版九年级数学下册3.1圆 同步达标测评 (word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.1圆 同步达标测评 (word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 150.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 00:00:00 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《3.1圆》同步达标测评(附答案)
一.选择题(共7小题,满分35分)
1.已知⊙O的半径是6cm,则⊙O中最长的弦长是( )
A.6cm B.12cm C.16cm D.20cm
2.已知AB是半径为5的圆的一条弦,则AB的长不可能是( )
A.4 B.8 C.10 D.12
3.下列说法:①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆.正确的说法有( )
A.1个 B.2个 C.3个 D.4个
4.如图所示,MN为⊙O的弦,∠N=50°,则∠MON的度数为( )
A.40° B.50° C.80° D.100°
5.AB=12cm,过A、B两点画半径为6cm的圆,能画的圆的个数为( )
A.0个 B.1个 C.2个 D.无数个
6.A、B是半径为5cm的⊙O上两个不同的点,则弦AB的取值范围是( )
A.AB>0 B.0<AB<5 C.0<AB<10 D.0<AB≤10
7.如图,AB是⊙O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连接AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
二.填空题(共7小题,满分35分)
8.如图所示,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,则图中共有劣弧 条,写出其中的两条优弧,如 .
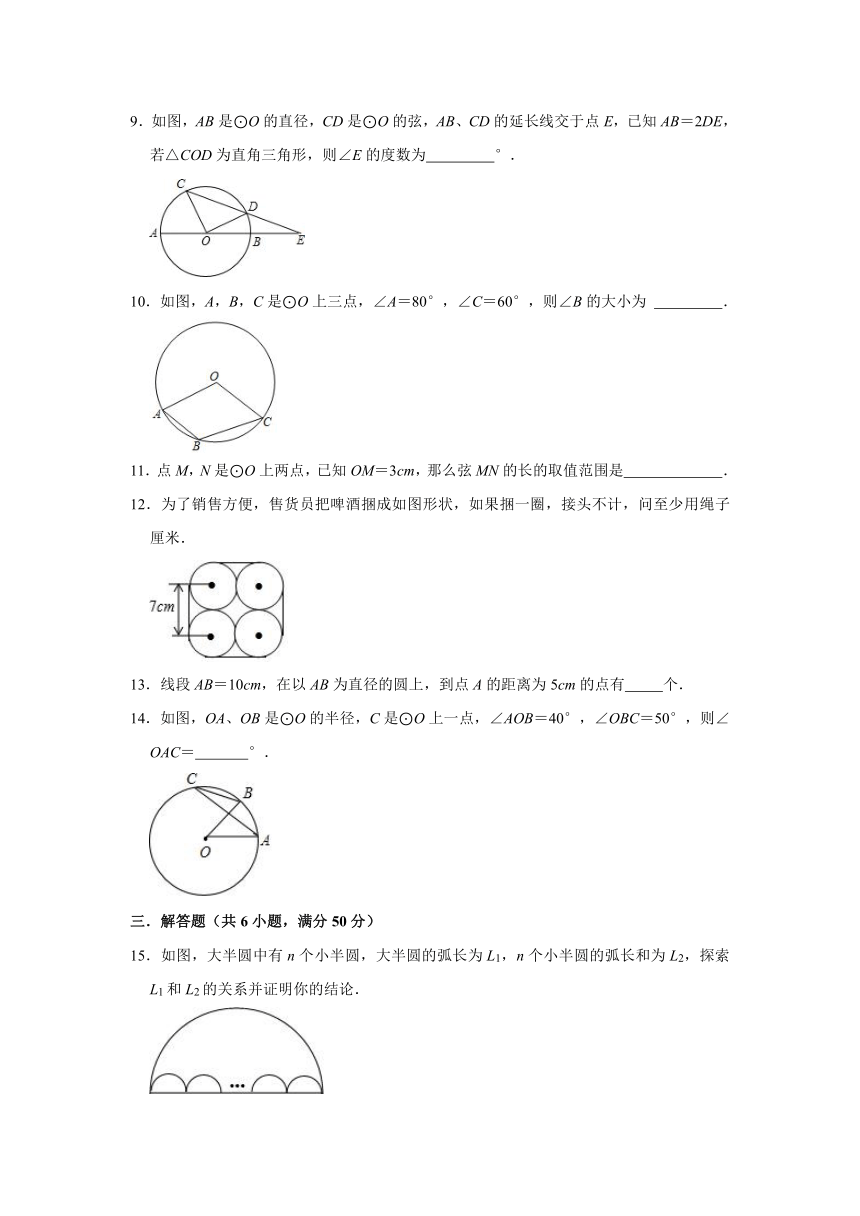
9.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,若△COD为直角三角形,则∠E的度数为 °.
10.如图,A,B,C是⊙O上三点,∠A=80°,∠C=60°,则∠B的大小为 .
11.点M,N是⊙O上两点,已知OM=3cm,那么弦MN的长的取值范围是 .
12.为了销售方便,售货员把啤酒捆成如图形状,如果捆一圈,接头不计,问至少用绳子 厘米.
13.线段AB=10cm,在以AB为直径的圆上,到点A的距离为5cm的点有 个.
14.如图,OA、OB是⊙O的半径,C是⊙O上一点,∠AOB=40°,∠OBC=50°,则∠OAC= °.
三.解答题(共6小题,满分50分)
15.如图,大半圆中有n个小半圆,大半圆的弧长为L1,n个小半圆的弧长和为L2,探索L1和L2的关系并证明你的结论.
16.A,B两点的距离为4厘米,用图形表示具有下列性质的点的集合,并指出它们是怎样的图形:
(1)到点A的距离等于3厘米的点的集合;
(2)到点B的距离等于3厘米的点的集合;
(3)到A,B两点的距离都等于3厘米的点的集合;
(4)到A,B两点的距离都不大于3厘米的点的集合.
17.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC.
(1)求∠AOB的度数.
(2)求∠EOD的度数.
18.如图,⊙O的半径OC⊥AB,D为上一点,DE⊥OC,DF⊥AB,垂足分别为E、F,EF=3,求直径AB的长.
19.已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
20.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
参考答案
一.选择题(共7小题,满分35分)
1.解:∵圆的直径为圆中最长的弦,
∴⊙O中最长的弦长为12cm.
故选:B.
2.解:因为圆中最长的弦为直径,所以弦长L≤10.
故选:D.
3.解:①直径是弦,正确,符合题意;
②弦不一定是直径,错误,不符合题意;
③半径相等的两个半圆是等弧,正确,符合题意;
④能够完全重合的两条弧是等弧,故原命题错误,不符合题意;
⑤根据半圆的定义可知,半圆是弧,但弧不一定是半圆,正确,符合题意,
正确的有3个,
故选:C.
4.解:∵OM=ON,
∴∠M=∠N=50°,
∴∠MON=180°﹣2×50°=80°.
故选:C.
5.解:这样的圆能画1个.如图:
作AB的垂直平分线l,交AB于O点,然后以O为圆心,以6cm为半径作圆,
则⊙O为所求;
故选:B.
6.解:∵圆中最长的弦为直径,
∴0<AB≤10.
故选:D.
7.解:∵AD∥OC,
∴∠AOC=∠DAO=70°,
又∵OD=OA,
∴∠ADO=∠DAO=70°,
∴∠AOD=180﹣70°﹣70°=40°.
故选:D.
二.填空题(共7小题,满分35分)
8.解:∵AB为直径,
∴图中劣弧有:、、、、,图中优弧有:,,,,
故答案为5;,
9.解:∵AB是⊙O的直径,
∵AB=2DO,
而AB=2DE,
∴DO=DE,
∴∠DOE=∠E,
∵△COD为直角三角形,
而OC=OD,
∴△COD为等腰直角三角形,
∴∠CDO=45°,
∵∠CDO=∠DOE+∠E,
∴∠E=∠CDO=22.5°.
故答案为22.5°.
10.解:连接OB,如图,
∵OA=OB,
∴∠A=∠OBA=80°,
∵OB=OC,
∴∠OBC=∠C=60°,
∴∠ABC=∠OBA+∠OBC=80°+60°=140°.
故答案为140°.
11.解:∵M、N是⊙O上两点,OM=3cm,
∴圆的半径为3cm,圆的直径为6cm,
∴0<MN≤6cm.
故答案为:0<MN≤6cm
12.解:如图所示:圆的直径为:7cm.
则根据题意得:7×4+7π=28+7π≈49.98(cm)
答:捆一圈至少用绳子49.98cm.
13.解:如图所示:到点A的距离为5cm的点有2个.
故答案为:2.
14.解:连接OC,
∵OC=OB,
∴∠OCB=∠OBC=50°,
∴∠BOC=180°﹣50°×2=80°,
∴∠AOC=80°+40°=120°,
∵OC=OA,
∴∠OAC=∠OCA=30°,
故答案为:30.
三.解答题(共6小题,满分50分)
15.解:L1=L2.理由如下:
设n个小半圆半径依次为r1,r2,…,rn.
则大圆半径为(r1+r2+…+rn)
∴L1=π(r1+r2+…+rn),
L2=πr1+πr2+…+πrn
=π(r1+r2+…+rn),
∴L1=L2.
16.解:(1)与点A的距离为3cm的点的集合;
(2)与点B的距离为3cm的点的集合;
(3)点C、D即为符合条件的点的集合;
(4)图中阴影部分即为符合条件的点的集合(含边界).
17.解:(1)连OB,如图,
∵AB=OC,OB=OC,
∴AB=BO,
∴∠AOB=∠1=∠A=20°;
(2)∵∠2=∠A+∠1,
∴∠2=2∠A,
∵OB=OE,
∴∠2=∠E,
∴∠E=2∠A,
∴∠DOE=∠A+∠E=3∠A=60°.
18.解:∵OC⊥AB,DE⊥OC,DF⊥AB,
∴四边形OFDE是矩形,
∴OD=EF=3,
∴AB=6.
19.解:AC与BD相等.理由如下:
连接OC、OD,如图,
∵OA=OB,AE=BF,
∴OE=OF,
∵CE⊥AB,DF⊥AB,
∴∠OEC=∠OFD=90°,
在Rt△OEC和Rt△OFD中,
,
∴Rt△OEC≌Rt△OFD(HL),
∴∠COE=∠DOF,
∴=,
∴AC=BD.
20.解:∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
一.选择题(共7小题,满分35分)
1.已知⊙O的半径是6cm,则⊙O中最长的弦长是( )
A.6cm B.12cm C.16cm D.20cm
2.已知AB是半径为5的圆的一条弦,则AB的长不可能是( )
A.4 B.8 C.10 D.12
3.下列说法:①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆.正确的说法有( )
A.1个 B.2个 C.3个 D.4个
4.如图所示,MN为⊙O的弦,∠N=50°,则∠MON的度数为( )
A.40° B.50° C.80° D.100°
5.AB=12cm,过A、B两点画半径为6cm的圆,能画的圆的个数为( )
A.0个 B.1个 C.2个 D.无数个
6.A、B是半径为5cm的⊙O上两个不同的点,则弦AB的取值范围是( )
A.AB>0 B.0<AB<5 C.0<AB<10 D.0<AB≤10
7.如图,AB是⊙O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连接AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
二.填空题(共7小题,满分35分)
8.如图所示,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,则图中共有劣弧 条,写出其中的两条优弧,如 .
9.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,若△COD为直角三角形,则∠E的度数为 °.
10.如图,A,B,C是⊙O上三点,∠A=80°,∠C=60°,则∠B的大小为 .
11.点M,N是⊙O上两点,已知OM=3cm,那么弦MN的长的取值范围是 .
12.为了销售方便,售货员把啤酒捆成如图形状,如果捆一圈,接头不计,问至少用绳子 厘米.
13.线段AB=10cm,在以AB为直径的圆上,到点A的距离为5cm的点有 个.
14.如图,OA、OB是⊙O的半径,C是⊙O上一点,∠AOB=40°,∠OBC=50°,则∠OAC= °.
三.解答题(共6小题,满分50分)
15.如图,大半圆中有n个小半圆,大半圆的弧长为L1,n个小半圆的弧长和为L2,探索L1和L2的关系并证明你的结论.
16.A,B两点的距离为4厘米,用图形表示具有下列性质的点的集合,并指出它们是怎样的图形:
(1)到点A的距离等于3厘米的点的集合;
(2)到点B的距离等于3厘米的点的集合;
(3)到A,B两点的距离都等于3厘米的点的集合;
(4)到A,B两点的距离都不大于3厘米的点的集合.
17.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC.
(1)求∠AOB的度数.
(2)求∠EOD的度数.
18.如图,⊙O的半径OC⊥AB,D为上一点,DE⊥OC,DF⊥AB,垂足分别为E、F,EF=3,求直径AB的长.
19.已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
20.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
参考答案
一.选择题(共7小题,满分35分)
1.解:∵圆的直径为圆中最长的弦,
∴⊙O中最长的弦长为12cm.
故选:B.
2.解:因为圆中最长的弦为直径,所以弦长L≤10.
故选:D.
3.解:①直径是弦,正确,符合题意;
②弦不一定是直径,错误,不符合题意;
③半径相等的两个半圆是等弧,正确,符合题意;
④能够完全重合的两条弧是等弧,故原命题错误,不符合题意;
⑤根据半圆的定义可知,半圆是弧,但弧不一定是半圆,正确,符合题意,
正确的有3个,
故选:C.
4.解:∵OM=ON,
∴∠M=∠N=50°,
∴∠MON=180°﹣2×50°=80°.
故选:C.
5.解:这样的圆能画1个.如图:
作AB的垂直平分线l,交AB于O点,然后以O为圆心,以6cm为半径作圆,
则⊙O为所求;
故选:B.
6.解:∵圆中最长的弦为直径,
∴0<AB≤10.
故选:D.
7.解:∵AD∥OC,
∴∠AOC=∠DAO=70°,
又∵OD=OA,
∴∠ADO=∠DAO=70°,
∴∠AOD=180﹣70°﹣70°=40°.
故选:D.
二.填空题(共7小题,满分35分)
8.解:∵AB为直径,
∴图中劣弧有:、、、、,图中优弧有:,,,,
故答案为5;,
9.解:∵AB是⊙O的直径,
∵AB=2DO,
而AB=2DE,
∴DO=DE,
∴∠DOE=∠E,
∵△COD为直角三角形,
而OC=OD,
∴△COD为等腰直角三角形,
∴∠CDO=45°,
∵∠CDO=∠DOE+∠E,
∴∠E=∠CDO=22.5°.
故答案为22.5°.
10.解:连接OB,如图,
∵OA=OB,
∴∠A=∠OBA=80°,
∵OB=OC,
∴∠OBC=∠C=60°,
∴∠ABC=∠OBA+∠OBC=80°+60°=140°.
故答案为140°.
11.解:∵M、N是⊙O上两点,OM=3cm,
∴圆的半径为3cm,圆的直径为6cm,
∴0<MN≤6cm.
故答案为:0<MN≤6cm
12.解:如图所示:圆的直径为:7cm.
则根据题意得:7×4+7π=28+7π≈49.98(cm)
答:捆一圈至少用绳子49.98cm.
13.解:如图所示:到点A的距离为5cm的点有2个.
故答案为:2.
14.解:连接OC,
∵OC=OB,
∴∠OCB=∠OBC=50°,
∴∠BOC=180°﹣50°×2=80°,
∴∠AOC=80°+40°=120°,
∵OC=OA,
∴∠OAC=∠OCA=30°,
故答案为:30.
三.解答题(共6小题,满分50分)
15.解:L1=L2.理由如下:
设n个小半圆半径依次为r1,r2,…,rn.
则大圆半径为(r1+r2+…+rn)
∴L1=π(r1+r2+…+rn),
L2=πr1+πr2+…+πrn
=π(r1+r2+…+rn),
∴L1=L2.
16.解:(1)与点A的距离为3cm的点的集合;
(2)与点B的距离为3cm的点的集合;
(3)点C、D即为符合条件的点的集合;
(4)图中阴影部分即为符合条件的点的集合(含边界).
17.解:(1)连OB,如图,
∵AB=OC,OB=OC,
∴AB=BO,
∴∠AOB=∠1=∠A=20°;
(2)∵∠2=∠A+∠1,
∴∠2=2∠A,
∵OB=OE,
∴∠2=∠E,
∴∠E=2∠A,
∴∠DOE=∠A+∠E=3∠A=60°.
18.解:∵OC⊥AB,DE⊥OC,DF⊥AB,
∴四边形OFDE是矩形,
∴OD=EF=3,
∴AB=6.
19.解:AC与BD相等.理由如下:
连接OC、OD,如图,
∵OA=OB,AE=BF,
∴OE=OF,
∵CE⊥AB,DF⊥AB,
∴∠OEC=∠OFD=90°,
在Rt△OEC和Rt△OFD中,
,
∴Rt△OEC≌Rt△OFD(HL),
∴∠COE=∠DOF,
∴=,
∴AC=BD.
20.解:∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
