2021—2022学年北师大版数学九年级下册 3.2圆的对称性 解答题专题训练 (word版含答案)
文档属性
| 名称 | 2021—2022学年北师大版数学九年级下册 3.2圆的对称性 解答题专题训练 (word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 509.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 18:24:30 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《3.2圆的对称性》解答题专题训练(附答案)
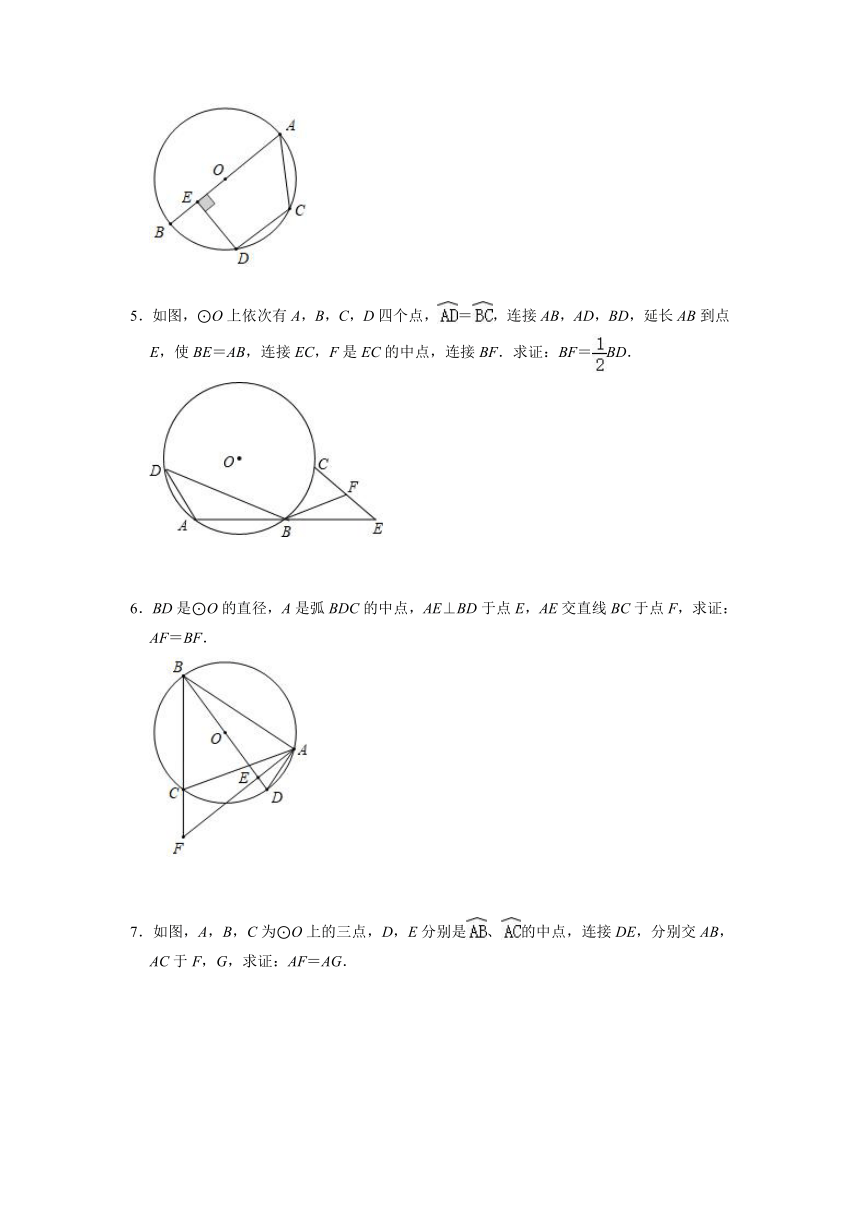
1.如图,BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,BE交AD于点F,且=,求证:AF=BF.
2.如图所示,⊙O中弦AB所对的劣弧为圆的,延长AB到C,使OC=AB,OC交⊙O于D,求的度数.
3.如图,在⊙O中,C,D是直径AB上的两点,且AC=BD,EG⊥AB,FH⊥AB,交AB于C、D,点E,G,F,H在⊙O上.
(1)若EG=8,AC=2,求⊙O半径;
(2)求证:=;
(3)若C,D分别为OA,OB的中点,则==成立吗?请说明理由.
4.如图,AB是⊙O的直径,AC是弦,=,DE⊥AB于点E,连接CD.
(1)求证:AC=2OE;
(2)若CD=2,DE=4,求AC的长.
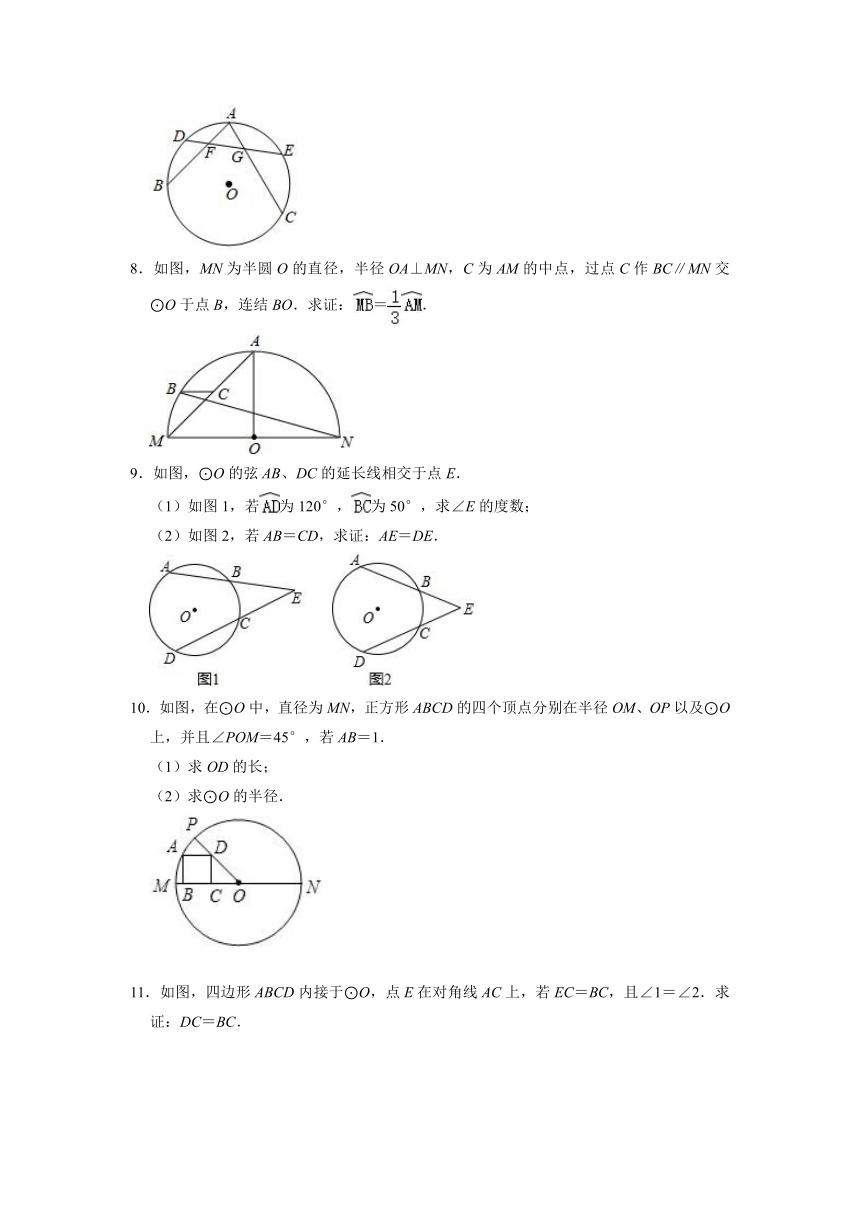
5.如图,⊙O上依次有A,B,C,D四个点,=,连接AB,AD,BD,延长AB到点E,使BE=AB,连接EC,F是EC的中点,连接BF.求证:BF=BD.
6.BD是⊙O的直径,A是弧BDC的中点,AE⊥BD于点E,AE交直线BC于点F,求证:AF=BF.
7.如图,A,B,C为⊙O上的三点,D,E分别是、的中点,连接DE,分别交AB,AC于F,G,求证:AF=AG.
8.如图,MN为半圆O的直径,半径OA⊥MN,C为AM的中点,过点C作BC∥MN交⊙O于点B,连结BO.求证:=.
9.如图,⊙O的弦AB、DC的延长线相交于点E.
(1)如图1,若为120°,为50°,求∠E的度数;
(2)如图2,若AB=CD,求证:AE=DE.
10.如图,在⊙O中,直径为MN,正方形ABCD的四个顶点分别在半径OM、OP以及⊙O上,并且∠POM=45°,若AB=1.
(1)求OD的长;
(2)求⊙O的半径.
11.如图,四边形ABCD内接于⊙O,点E在对角线AC上,若EC=BC,且∠1=∠2.求证:DC=BC.
12.如图,在△ACE中,AC=CE,⊙O经过点A,C,且与边AE,CE分别交于点D,F,点B是劣弧AC上的一点,且=,连接AB,BC,CD.求证:△CDE≌△ABC.
13.如图,已知AB,CG是⊙O的两条直径,AB⊥CD于点E,CG⊥AD于点F.
(1)求∠AOG的度数;
(2)若AB=2,求CD的长.
14.如图,在⊙O中,点C是优弧ACB的中点,D、E分别是OA、OB上的点,且AD=BE,弦CM、CN分别过点D、E.
(1)求证:CD=CE.
(2)求证:=.
15.如图,点A、B、C在⊙O上,=.
(1)若D、E分别是半径OA、OB的中点,如图1,求证:CD=CE.
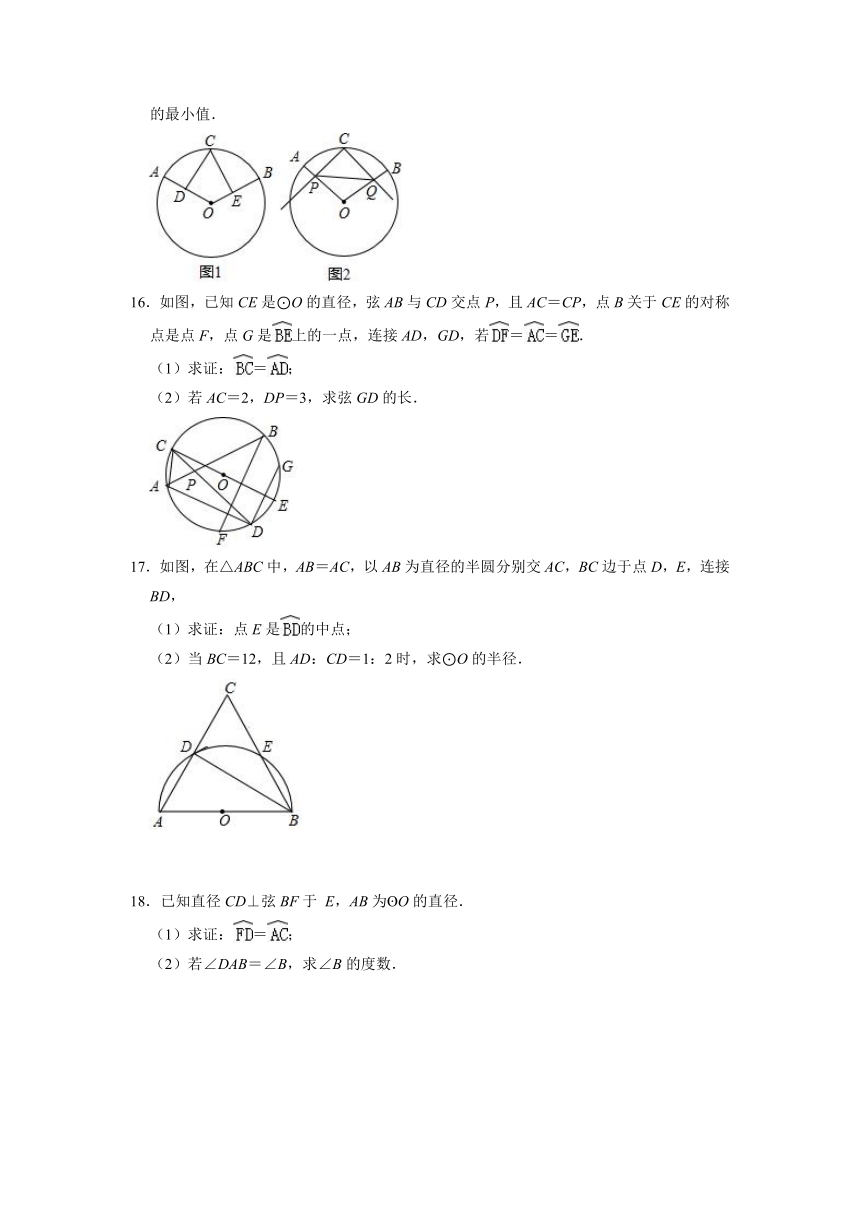
(2)如图2,⊙O的半径为4,∠AOB=90°,点P是线段OA上的一个动点(与点A、O不重合),将射线CP绕点C逆时针旋转90°,与OB相交于点Q,连接PQ,求出PQ的最小值.
16.如图,已知CE是⊙O的直径,弦AB与CD交点P,且AC=CP,点B关于CE的对称点是点F,点G是上的一点,连接AD,GD,若==.
(1)求证:=;
(2)若AC=2,DP=3,求弦GD的长.
17.如图,在△ABC中,AB=AC,以AB为直径的半圆分别交AC,BC边于点D,E,连接BD,
(1)求证:点E是的中点;
(2)当BC=12,且AD:CD=1:2时,求⊙O的半径.
18.已知直径CD⊥弦BF于 E,AB为 O的直径.
(1)求证:=;
(2)若∠DAB=∠B,求∠B的度数.
19.如图,AB,CD是⊙O的两条直径,过点A作AE∥CD交⊙O于点E,连接BD,DE,求证:BD=DE.
20.如图,AB是⊙O的直径,C、P是弧AB上两点,AB=25,AC=7.
(1)如图(1),若点P是弧AB的中点,求PA的长;
(2)如图(2),若点P是弧BC的中点,求PA的长.
参考答案
1.证明:延长AD交⊙O于M,
∵BC⊥AD,BC过圆心O,
∴=,
∵=,
∴=,
∴∠BAF=∠ABF,
∴AF=BF.
2.解:过O点作OH⊥AB于H,如图,
∵弦AB所对的劣弧为圆的,
∴∠AOB=×360°=90°,
而OA=OB,
∴△OAB为等腰直角三角形,
∴OH=AB,∠BOH=45°,
∵OC=AB,
∴OH=OC,
在Rt△OCH中,cos∠COH==,
∴∠COH=60°,
∴∠BOD=∠COH﹣∠BOH=60°﹣45°=15°,
∴的度数为15°.
3.解:(1)连接EO,
设⊙O半径为r,
∵EG⊥AB,
∴CE=CG=EG=4,
∵AC=2,
∴OC=r﹣2,
在Rt△CEO中,OE2=CE2+OC2,
∴r2=42+(r﹣2)2,
解得r=5,
∴⊙O半径为5;
(2)连接OE、OF,
∵AC=BD,OA=OB,
∴OC=OD,
∵EG⊥AB,FH⊥AB,
∴在Rt△COE和Rt△DOF中,
,
∴Rt△COE≌Rt△DOF(HL),
∴∠AOE=∠BOF,
∴=;
(3)==成立,理由如下:
∵C,D分别为OA,OB的中点,
∴OC=,
∴cos∠AOE==,
∴∠AOE=60°,
同理∠BOF=60°,
∴∠EOF=60°,
∴==.
4.(1)证明:连接AD和BD,过D作DM⊥AC,交AC的延长线于M,
∵=,
∴BD=CD,∠BAD=∠MAD,
∵DM⊥AC,DE⊥AB,
∴∠M=∠AED=∠BED=90°,DE=DM,
∵四边形ACDB是⊙O的内接四边形,
∴∠DCM=∠B,
在△BED和△CMD中,
,
∴△BED≌△CMD(AAS),
∴BE=CM,
在Rt△AED和Rt△AMD中,
,
∴Rt△AED≌Rt△AMD(HL),
∴AE=AM,
∵AE=OA+OE=OB+OE,AM=AC+CM=AC+BE=AC+OB﹣OE,
∴OB+OE=AC+OB﹣OE,
即AC=2OE;
(2)解:连接OD,设⊙O的半径为R,则OB=OD=R,
∵CD=2,BD=CD,
∴BD=2,
在Rt△DEB中,由勾股定理得:BE===2,
在Rt△OED中,由勾股定理得:OD2=OE2+DE2,
即R2=(R﹣2)2+42,
解得:R=5,
即OE=5﹣2=3,
由(1)知:AC=2OE,
∴AC=6.
5.证明:连接AC,
∵AB=BE,
∴点B为AE的中点,
∵F是EC的中点,
∴BF为△EAC的中位线,
∴BF=AC,
∵=,
∴=,
∴BD=AC,
∴BF=BD.
6.证明:如图,设AF交⊙O于点T,连接BT.
∵BD是直径,BD⊥AT,
∴AE=ET,
∴BT=BA,
∴∠BAT=∠BTA,
∵A是弧BDC的中点,
∴=,
∴AB=AC,
∴∠ACB=∠ABC,
∵∠ACB=∠ATB,
∴∠TAB=∠CBA,
∴AF=BF.
7.证明:连接OD和OE交AB于M点,交AC于N点,
∵D为的中点,OD过圆心O点,
∴OD⊥AB.
同理OE⊥AC,
∵OD=OE,
∴∠ODE=∠OED,
∴90°﹣∠ODE=90°﹣∠OED,即∠DFM=∠EGN,
∵∠DFM=∠AFE,∠EGN=∠AGF,
∴∠AFE=∠AGF,
∴AF=AG.
8.解:延长BC交OA于H,连接OB,如图,
∵OA⊥MN,BC∥OA,
∴BH⊥OA,
∵C点为AM的中点,
∴H点为OA的中点,
即OH=OA,
在Rt△OBH中,∵cos∠BOH==,
∴∠BOH=60°,
∴∠BOM=30°,
即∠BOM=∠AOM,
∴=.
9.(1)解:连接AC.
∵为120°,为50°,
∴∠ACD=60°,∠BAC=25°,
∵∠ACD=∠BAC+∠E
∴∠E=∠ACD﹣∠BAC=60°﹣25°=35°;
(2)证明:连接AD.
∵AB=CD,
∴=,
∴=,
∴∠ADC=∠DAB,
∴AE=DE.
10.解:(1)如图,
∵四边形ABCD 为正方形,
∴DC=BC=AB=1,∠DCO=∠ABC=90°,
∵∠POM=45°,
∴CO=DC=1,
∴OD=CO==;
(2)BO=BC+CO=BC+CD=1+1=2,
连接AO,
则△ABO 为直角三角形,
于是 AO=.
即⊙O的半径为.
11.证明:∵EC=BC,
∴∠CBE=∠CEB,
∴∠1+∠CBD=∠2+∠BAC,
∵∠1=∠2,
∴∠CBD=∠BAC,
∵∠BAC=∠BDC,
∴∠CBD=∠BDC,
∴BC=CD.
12.证明:∵四边形ABCD内接于⊙O,
∴∠ABC=∠CDE,
∵=,
∴∠BAC=∠DCE,
在△CDE和△ABC中,
,
∴△CDE≌△ABC(AAS).
13.解:(1)连接OD,
∵AB⊥CD,
∴=,
∴∠BOC=∠BOD,
由圆周角定理得,∠A=∠BOD,
∴∠A=∠BOD,
∵∠AOG=∠BOD,
∴∠A=∠AOG,
∵∠OFA=90°,
∴∠AOG=60°;
(2)∵∠AOG=60°,
∴∠COE=60°,
∴∠C=30°,
∴OE=OC=,
∴CE==,
∵AB⊥CD,
∴CD=2CE=.
14.(1)证明:连接OC.
∵=,
∴∠COD=∠COE,
∵OA=OB,AD=BE,
∴OD=OE,∵OC=OC,
∴△COD≌△COE(SAS),
∴CD=CE.
(2)分别连接OM,ON,
∵△COD≌△COE,
∴∠CDO=∠CEO,∠OCD=∠OCE,
∵OC=OM=ON,
∴∠OCM=∠OMC,∠OCN=∠ONC,
∴∠OMD=∠ONE,
∵∠ODC=∠DMO+∠MOD,∠CEO=∠CNO+∠EON,
∴∠MOD=∠NOE,
∴=.
15.解:(1)连接CO.
∵=,
∴∠AOC=∠BOC,
∵D、E分别是半径OA、OB的中点,
∴,,
∴OD=OE,
在△ODC和△OEC中,
∵OD=OE,∠AOC=∠BOC,OC=OC,
∴△ODC≌△OEC(SAS)
∴CD=CE;
(2)当CP⊥OA时,∵∠AOB=90°,∠PCQ=90°,
∴∠CQO=90°,即CQ⊥OB.
∵∠AOC=∠BOC,
∴CP=CQ,
当CP与OA不垂直时,
如图,过点C作CM⊥OA,CN⊥OB,M、N为垂足.
∵∠AOC=∠BOC,
∴CM=CN,
又∵∠AOB=90°,
∴∠MCN=90°,
∴四边形CMON是正方形,
∵∠PCQ=90°,
∴∠PCM=∠QCN,
∴△PCM≌△QCN(AAS)
∴CP=CQ,
∴,
∴当CP取得最小值即CM的长时,PQ有最小值,
∴,PQ的最小值为4.
16.(1)证明:∵点B关于CE的对称点是点F,
∴EC⊥BF,
∴=,
∵=,
∴=,
∴=.
(2)连接BC、BE、BD,作CH⊥AB于H.
∵CA=CP,
∴∠CAP=∠CPA,∠CPA=∠BPD,
∵∠CAP=∠BDP,
∴∠BPD=∠BDP,
∴BP=BD,
∵=,
∴∠ABD=∠CDB,
∴PB=PD,
∴PB=PD=BD,
∴△PDB是等边三角形,
∴∠BDP=∠BPD=∠APC=60°,
∴△ACP是等边三角形,
∵AC=2,PD=3,CH⊥AP,
∴AH=PH=2,BH=PB+PH=3,CH=,
∴BC==,
∵∠CEB=∠CDB=60°,EC是直径,
∴∠CBE=90°,
∴BE=BC tan30°=,
∵EC⊥BF,
∴=,
∵=,
∴=,
∴=,
∴DG=BE=.
17.(1)证明:连接AE,DE
∵AB是直径,
∴AE⊥BC,
∵AB=AC,
∴BE=EC,
∵∠CDB=90°,DE是斜边BC的中线,
∴DE=EB,
∴,
即点E是的中点;
(2)设AD=x,则CD=2x,
∴AB=AC=3x,
∵AB为直径,
∴∠ADB=90°,
∴BD2=(3x)2﹣x2=8x2,
在Rt△CDB中,
(2x)2+8x2=122,
∴,
∴,
即⊙O的半径是3.
18.(1)证明:∵直径CD⊥弦BF,
∴=,
∵∠AOC=∠BOD,
∴=,
∴=;
(2)解:由圆周角定理得,∠BOD=2∠DAB,
∵∠DAB=∠B,
∴∠BOD=2∠B,
∵CD⊥BF,
∴∠B=30°.
19.证明:连接OE,如图,
∵OA=OE,∴∠A=∠OEA,
∵AE∥CD,∴∠BOD=∠A,∠DOE=∠OEA,
∴∠BOD=∠DOE,
∴BD=DE.
20.解:(1)如图(1)所示,连接PB,
∵AB是⊙O的直径且P是的中点,
∴∠PAB=∠PBA=45°,∠APB=90°,
又∵在等腰三角形△APB中有AB=25,
∴PA==;
(2)如图(2)所示:连接BC.OP相交于M点,作PN⊥AB于点N,
∵P点为弧BC的中点,
∴OP⊥BC,∠OMB=90°,
又因为AB为直径,
∴∠ACB=90°,
∴∠ACB=∠OMB,
∴OP∥AC,
∴∠CAB=∠POB,
又因为∠ACB=∠ONP=90°,
∴△ACB∽△ONP
∴=,
又∵AB=25,AC=7,OP=,
代入得 ON=,
∴AN=OA+ON=16,
∴在Rt△OPN中,有NP2=OP2﹣ON2=144
在Rt△ANP中 有PA==20
∴PA=20.
1.如图,BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,BE交AD于点F,且=,求证:AF=BF.
2.如图所示,⊙O中弦AB所对的劣弧为圆的,延长AB到C,使OC=AB,OC交⊙O于D,求的度数.
3.如图,在⊙O中,C,D是直径AB上的两点,且AC=BD,EG⊥AB,FH⊥AB,交AB于C、D,点E,G,F,H在⊙O上.
(1)若EG=8,AC=2,求⊙O半径;
(2)求证:=;
(3)若C,D分别为OA,OB的中点,则==成立吗?请说明理由.
4.如图,AB是⊙O的直径,AC是弦,=,DE⊥AB于点E,连接CD.
(1)求证:AC=2OE;
(2)若CD=2,DE=4,求AC的长.
5.如图,⊙O上依次有A,B,C,D四个点,=,连接AB,AD,BD,延长AB到点E,使BE=AB,连接EC,F是EC的中点,连接BF.求证:BF=BD.
6.BD是⊙O的直径,A是弧BDC的中点,AE⊥BD于点E,AE交直线BC于点F,求证:AF=BF.
7.如图,A,B,C为⊙O上的三点,D,E分别是、的中点,连接DE,分别交AB,AC于F,G,求证:AF=AG.
8.如图,MN为半圆O的直径,半径OA⊥MN,C为AM的中点,过点C作BC∥MN交⊙O于点B,连结BO.求证:=.
9.如图,⊙O的弦AB、DC的延长线相交于点E.
(1)如图1,若为120°,为50°,求∠E的度数;
(2)如图2,若AB=CD,求证:AE=DE.
10.如图,在⊙O中,直径为MN,正方形ABCD的四个顶点分别在半径OM、OP以及⊙O上,并且∠POM=45°,若AB=1.
(1)求OD的长;
(2)求⊙O的半径.
11.如图,四边形ABCD内接于⊙O,点E在对角线AC上,若EC=BC,且∠1=∠2.求证:DC=BC.
12.如图,在△ACE中,AC=CE,⊙O经过点A,C,且与边AE,CE分别交于点D,F,点B是劣弧AC上的一点,且=,连接AB,BC,CD.求证:△CDE≌△ABC.
13.如图,已知AB,CG是⊙O的两条直径,AB⊥CD于点E,CG⊥AD于点F.
(1)求∠AOG的度数;
(2)若AB=2,求CD的长.
14.如图,在⊙O中,点C是优弧ACB的中点,D、E分别是OA、OB上的点,且AD=BE,弦CM、CN分别过点D、E.
(1)求证:CD=CE.
(2)求证:=.
15.如图,点A、B、C在⊙O上,=.
(1)若D、E分别是半径OA、OB的中点,如图1,求证:CD=CE.
(2)如图2,⊙O的半径为4,∠AOB=90°,点P是线段OA上的一个动点(与点A、O不重合),将射线CP绕点C逆时针旋转90°,与OB相交于点Q,连接PQ,求出PQ的最小值.
16.如图,已知CE是⊙O的直径,弦AB与CD交点P,且AC=CP,点B关于CE的对称点是点F,点G是上的一点,连接AD,GD,若==.
(1)求证:=;
(2)若AC=2,DP=3,求弦GD的长.
17.如图,在△ABC中,AB=AC,以AB为直径的半圆分别交AC,BC边于点D,E,连接BD,
(1)求证:点E是的中点;
(2)当BC=12,且AD:CD=1:2时,求⊙O的半径.
18.已知直径CD⊥弦BF于 E,AB为 O的直径.
(1)求证:=;
(2)若∠DAB=∠B,求∠B的度数.
19.如图,AB,CD是⊙O的两条直径,过点A作AE∥CD交⊙O于点E,连接BD,DE,求证:BD=DE.
20.如图,AB是⊙O的直径,C、P是弧AB上两点,AB=25,AC=7.
(1)如图(1),若点P是弧AB的中点,求PA的长;
(2)如图(2),若点P是弧BC的中点,求PA的长.
参考答案
1.证明:延长AD交⊙O于M,
∵BC⊥AD,BC过圆心O,
∴=,
∵=,
∴=,
∴∠BAF=∠ABF,
∴AF=BF.
2.解:过O点作OH⊥AB于H,如图,
∵弦AB所对的劣弧为圆的,
∴∠AOB=×360°=90°,
而OA=OB,
∴△OAB为等腰直角三角形,
∴OH=AB,∠BOH=45°,
∵OC=AB,
∴OH=OC,
在Rt△OCH中,cos∠COH==,
∴∠COH=60°,
∴∠BOD=∠COH﹣∠BOH=60°﹣45°=15°,
∴的度数为15°.
3.解:(1)连接EO,
设⊙O半径为r,
∵EG⊥AB,
∴CE=CG=EG=4,
∵AC=2,
∴OC=r﹣2,
在Rt△CEO中,OE2=CE2+OC2,
∴r2=42+(r﹣2)2,
解得r=5,
∴⊙O半径为5;
(2)连接OE、OF,
∵AC=BD,OA=OB,
∴OC=OD,
∵EG⊥AB,FH⊥AB,
∴在Rt△COE和Rt△DOF中,
,
∴Rt△COE≌Rt△DOF(HL),
∴∠AOE=∠BOF,
∴=;
(3)==成立,理由如下:
∵C,D分别为OA,OB的中点,
∴OC=,
∴cos∠AOE==,
∴∠AOE=60°,
同理∠BOF=60°,
∴∠EOF=60°,
∴==.
4.(1)证明:连接AD和BD,过D作DM⊥AC,交AC的延长线于M,
∵=,
∴BD=CD,∠BAD=∠MAD,
∵DM⊥AC,DE⊥AB,
∴∠M=∠AED=∠BED=90°,DE=DM,
∵四边形ACDB是⊙O的内接四边形,
∴∠DCM=∠B,
在△BED和△CMD中,
,
∴△BED≌△CMD(AAS),
∴BE=CM,
在Rt△AED和Rt△AMD中,
,
∴Rt△AED≌Rt△AMD(HL),
∴AE=AM,
∵AE=OA+OE=OB+OE,AM=AC+CM=AC+BE=AC+OB﹣OE,
∴OB+OE=AC+OB﹣OE,
即AC=2OE;
(2)解:连接OD,设⊙O的半径为R,则OB=OD=R,
∵CD=2,BD=CD,
∴BD=2,
在Rt△DEB中,由勾股定理得:BE===2,
在Rt△OED中,由勾股定理得:OD2=OE2+DE2,
即R2=(R﹣2)2+42,
解得:R=5,
即OE=5﹣2=3,
由(1)知:AC=2OE,
∴AC=6.
5.证明:连接AC,
∵AB=BE,
∴点B为AE的中点,
∵F是EC的中点,
∴BF为△EAC的中位线,
∴BF=AC,
∵=,
∴=,
∴BD=AC,
∴BF=BD.
6.证明:如图,设AF交⊙O于点T,连接BT.
∵BD是直径,BD⊥AT,
∴AE=ET,
∴BT=BA,
∴∠BAT=∠BTA,
∵A是弧BDC的中点,
∴=,
∴AB=AC,
∴∠ACB=∠ABC,
∵∠ACB=∠ATB,
∴∠TAB=∠CBA,
∴AF=BF.
7.证明:连接OD和OE交AB于M点,交AC于N点,
∵D为的中点,OD过圆心O点,
∴OD⊥AB.
同理OE⊥AC,
∵OD=OE,
∴∠ODE=∠OED,
∴90°﹣∠ODE=90°﹣∠OED,即∠DFM=∠EGN,
∵∠DFM=∠AFE,∠EGN=∠AGF,
∴∠AFE=∠AGF,
∴AF=AG.
8.解:延长BC交OA于H,连接OB,如图,
∵OA⊥MN,BC∥OA,
∴BH⊥OA,
∵C点为AM的中点,
∴H点为OA的中点,
即OH=OA,
在Rt△OBH中,∵cos∠BOH==,
∴∠BOH=60°,
∴∠BOM=30°,
即∠BOM=∠AOM,
∴=.
9.(1)解:连接AC.
∵为120°,为50°,
∴∠ACD=60°,∠BAC=25°,
∵∠ACD=∠BAC+∠E
∴∠E=∠ACD﹣∠BAC=60°﹣25°=35°;
(2)证明:连接AD.
∵AB=CD,
∴=,
∴=,
∴∠ADC=∠DAB,
∴AE=DE.
10.解:(1)如图,
∵四边形ABCD 为正方形,
∴DC=BC=AB=1,∠DCO=∠ABC=90°,
∵∠POM=45°,
∴CO=DC=1,
∴OD=CO==;
(2)BO=BC+CO=BC+CD=1+1=2,
连接AO,
则△ABO 为直角三角形,
于是 AO=.
即⊙O的半径为.
11.证明:∵EC=BC,
∴∠CBE=∠CEB,
∴∠1+∠CBD=∠2+∠BAC,
∵∠1=∠2,
∴∠CBD=∠BAC,
∵∠BAC=∠BDC,
∴∠CBD=∠BDC,
∴BC=CD.
12.证明:∵四边形ABCD内接于⊙O,
∴∠ABC=∠CDE,
∵=,
∴∠BAC=∠DCE,
在△CDE和△ABC中,
,
∴△CDE≌△ABC(AAS).
13.解:(1)连接OD,
∵AB⊥CD,
∴=,
∴∠BOC=∠BOD,
由圆周角定理得,∠A=∠BOD,
∴∠A=∠BOD,
∵∠AOG=∠BOD,
∴∠A=∠AOG,
∵∠OFA=90°,
∴∠AOG=60°;
(2)∵∠AOG=60°,
∴∠COE=60°,
∴∠C=30°,
∴OE=OC=,
∴CE==,
∵AB⊥CD,
∴CD=2CE=.
14.(1)证明:连接OC.
∵=,
∴∠COD=∠COE,
∵OA=OB,AD=BE,
∴OD=OE,∵OC=OC,
∴△COD≌△COE(SAS),
∴CD=CE.
(2)分别连接OM,ON,
∵△COD≌△COE,
∴∠CDO=∠CEO,∠OCD=∠OCE,
∵OC=OM=ON,
∴∠OCM=∠OMC,∠OCN=∠ONC,
∴∠OMD=∠ONE,
∵∠ODC=∠DMO+∠MOD,∠CEO=∠CNO+∠EON,
∴∠MOD=∠NOE,
∴=.
15.解:(1)连接CO.
∵=,
∴∠AOC=∠BOC,
∵D、E分别是半径OA、OB的中点,
∴,,
∴OD=OE,
在△ODC和△OEC中,
∵OD=OE,∠AOC=∠BOC,OC=OC,
∴△ODC≌△OEC(SAS)
∴CD=CE;
(2)当CP⊥OA时,∵∠AOB=90°,∠PCQ=90°,
∴∠CQO=90°,即CQ⊥OB.
∵∠AOC=∠BOC,
∴CP=CQ,
当CP与OA不垂直时,
如图,过点C作CM⊥OA,CN⊥OB,M、N为垂足.
∵∠AOC=∠BOC,
∴CM=CN,
又∵∠AOB=90°,
∴∠MCN=90°,
∴四边形CMON是正方形,
∵∠PCQ=90°,
∴∠PCM=∠QCN,
∴△PCM≌△QCN(AAS)
∴CP=CQ,
∴,
∴当CP取得最小值即CM的长时,PQ有最小值,
∴,PQ的最小值为4.
16.(1)证明:∵点B关于CE的对称点是点F,
∴EC⊥BF,
∴=,
∵=,
∴=,
∴=.
(2)连接BC、BE、BD,作CH⊥AB于H.
∵CA=CP,
∴∠CAP=∠CPA,∠CPA=∠BPD,
∵∠CAP=∠BDP,
∴∠BPD=∠BDP,
∴BP=BD,
∵=,
∴∠ABD=∠CDB,
∴PB=PD,
∴PB=PD=BD,
∴△PDB是等边三角形,
∴∠BDP=∠BPD=∠APC=60°,
∴△ACP是等边三角形,
∵AC=2,PD=3,CH⊥AP,
∴AH=PH=2,BH=PB+PH=3,CH=,
∴BC==,
∵∠CEB=∠CDB=60°,EC是直径,
∴∠CBE=90°,
∴BE=BC tan30°=,
∵EC⊥BF,
∴=,
∵=,
∴=,
∴=,
∴DG=BE=.
17.(1)证明:连接AE,DE
∵AB是直径,
∴AE⊥BC,
∵AB=AC,
∴BE=EC,
∵∠CDB=90°,DE是斜边BC的中线,
∴DE=EB,
∴,
即点E是的中点;
(2)设AD=x,则CD=2x,
∴AB=AC=3x,
∵AB为直径,
∴∠ADB=90°,
∴BD2=(3x)2﹣x2=8x2,
在Rt△CDB中,
(2x)2+8x2=122,
∴,
∴,
即⊙O的半径是3.
18.(1)证明:∵直径CD⊥弦BF,
∴=,
∵∠AOC=∠BOD,
∴=,
∴=;
(2)解:由圆周角定理得,∠BOD=2∠DAB,
∵∠DAB=∠B,
∴∠BOD=2∠B,
∵CD⊥BF,
∴∠B=30°.
19.证明:连接OE,如图,
∵OA=OE,∴∠A=∠OEA,
∵AE∥CD,∴∠BOD=∠A,∠DOE=∠OEA,
∴∠BOD=∠DOE,
∴BD=DE.
20.解:(1)如图(1)所示,连接PB,
∵AB是⊙O的直径且P是的中点,
∴∠PAB=∠PBA=45°,∠APB=90°,
又∵在等腰三角形△APB中有AB=25,
∴PA==;
(2)如图(2)所示:连接BC.OP相交于M点,作PN⊥AB于点N,
∵P点为弧BC的中点,
∴OP⊥BC,∠OMB=90°,
又因为AB为直径,
∴∠ACB=90°,
∴∠ACB=∠OMB,
∴OP∥AC,
∴∠CAB=∠POB,
又因为∠ACB=∠ONP=90°,
∴△ACB∽△ONP
∴=,
又∵AB=25,AC=7,OP=,
代入得 ON=,
∴AN=OA+ON=16,
∴在Rt△OPN中,有NP2=OP2﹣ON2=144
在Rt△ANP中 有PA==20
∴PA=20.
