2021-2022学年北师大版九年级数学下册3.3垂径定理 同步达标测评 (word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.3垂径定理 同步达标测评 (word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 304.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 00:00:00 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学下册《3.3垂径定理》同步达标测评(附答案)
一.选择题(共10小题,满分40分)
1.如图,在⊙O中,直径AB=10,弦DE⊥AB于点C,若OC:OB=3:5,连接DO,则DE的长为( )
A.3 B.4 C.6 D.8
2.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=6,CD=4,则AE的长为( )
A. B. C. D.
3.如图,弦CD垂直于⊙O的直径AB,垂足为H,且OB=13,CD=24,则OH的长是( )
A.3 B.4 C.5 D.6
4.AB和CD是⊙O的两条平行弦,AB=6,CD=8,⊙O的半径为5,则AB与CD间的距离为( )
A.1 B.7 C.1或7 D.3或4
5.在半径为50mm的⊙O中,弦AB的长为50mm,则点O到AB的距离为( )
A.50mm B.25mm C.25mm D.25mm
6.在直径为20cm的圆柱形油槽内装入一些油后,截面如图所示,若油槽面宽AB=16cm,则油的最大深度为( )
A.4cm B.6cm C.8cm D.10cm
7.如图,⊙O的弦AB=8,C是AB的中点,且OC=3,OC⊥AB,则⊙O的周长等于( )
A.4π B.5π C.8π D.10π
8.如图,在半径为10cm的圆形铁片上切下一块高为4cm的弓形铁片,则弓形弦AB的长为( )
A.8cm B.12cm C.16cm D.20cm
9.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径长是( )
A.2cm B.2.5cm C.3cm D.4cm
10.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )
A.2cm B.4cm C.2cm或4cm D.2cm或4cm
二.填空题(共6小题,满分30分)
11.已知⊙O的半径为13cm,弦AB的长为10cm,则圆心O到AB的距离为 cm.
12.如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为10,AB=16,则CD的长是 .
13.如图,⊙O的直径CD垂直弦AB于点E,且CE=3cm,DE=7cm,则弦AB= cm.
14.如图,在半径为5的⊙O中,弦AB=6,OP⊥AB,垂足为点P,则OP的长为 .
15.如图,⊙O的半径OA与弦BC交于点D.若OD=3,AD=2,BD=CD,则BC的长为 .
16.如图∠C=90°,⊙C与AB相交于点D,AC=5,CB=12,则AD= .
三.解答题(共8小题,满分50分)
17.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,求线段AE的长.
18.如图,在⊙O中,半径OC⊥弦AB,垂足为点D,AB=6,CD=1,求⊙O半径的长.
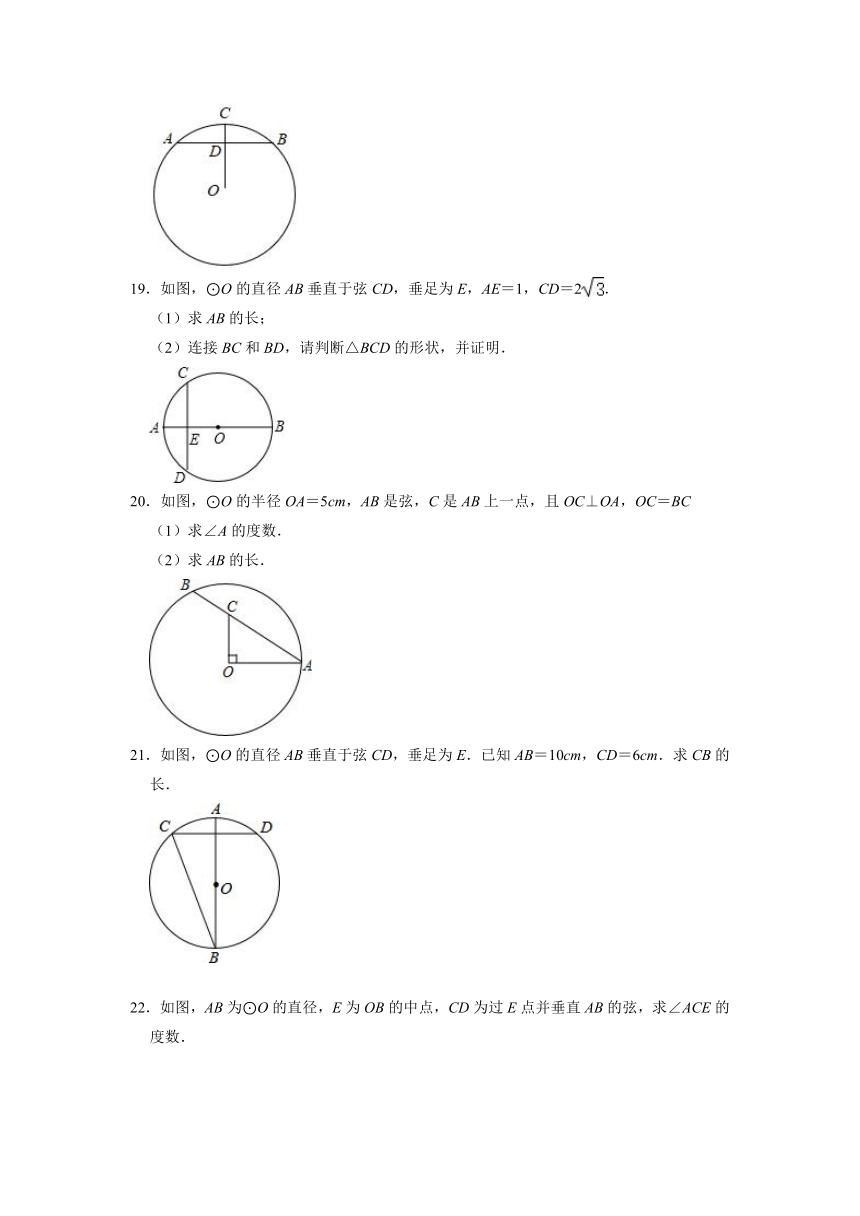
19.如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=1,CD=2.
(1)求AB的长;
(2)连接BC和BD,请判断△BCD的形状,并证明.
20.如图,⊙O的半径OA=5cm,AB是弦,C是AB上一点,且OC⊥OA,OC=BC
(1)求∠A的度数.
(2)求AB的长.
21.如图,⊙O的直径AB垂直于弦CD,垂足为E.已知AB=10cm,CD=6cm.求CB的长.
22.如图,AB为⊙O的直径,E为OB的中点,CD为过E点并垂直AB的弦,求∠ACE的度数.
23.如图,P是⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径.
参考答案
一.选择题(共10小题,满分40分)
1.解:∵AB=10,OC:OB=3:5,
∴OC=3,
在Rt△OCD中,CD===4,
∵DE⊥AB,
∴DE=2CD=8,
故选:D.
2.解:连接OC,如图,
∵CD⊥AB,
∴CE=DE=CD=2,
在Rt△OCE中,∵OC=3,CE=2,
∴OE==,
∴AE=OA+OE=3+.
故选:B.
3.解:连接OC,
∵AB是⊙O的直径,CD⊥AB,
∴CH=CD=12,
在Rt△OCH中,OH===5,
故选:C.
4.解:①当AB、CD在圆心两侧时;
过O作OE⊥CD交CD于E点,过O作OF⊥AB交AB于F点,连接OA、OC,如图所示:
∵半径r=5,弦AB∥CD,且AB=6,CD=8,
∴OA=OC=5,CE=DE=4,AF=FB=3,E、F、O在一条直线上,
∴EF为AB、CD之间的距离
在Rt△OEC中,由勾股定理可得:
OE2=OC2﹣CE2
∴OE==3,
在Rt△OFA中,由勾股定理可得:
OF2=OA2﹣AF2
∴OF==4,
∴EF=OE+OF=3+4=7,
AB与CD的距离为7;
②当AB、CD在圆心同侧时;
同①可得:OE=3,OF=4;
则AB与CD的距离为:OF﹣OE=1;
综上所述:AB与CD间的距离为1或7.
故选:C.
5.解:作OC⊥AB于C,
根据题意:OA=OB=AB=50mm,
∴△AOB是等边三角形,
∴∠AOC=30°,
∴OC=OA cos30°=25cm.
故选:B.
6.解:过圆心O向AB作垂线,交AB于点C.
根据勾股定理可得OC==6.
所以油的最大深度为10﹣6=4(cm).
故选:A.
7.解:连接OA,如图,
∵C是AB的中点,
∴AC=BC=AB=4,OC⊥AB,
在Rt△OAC中,OA===5,
∴⊙O的周长=2π×5=10π.
故选:D.
8.解:如图,过O作OD⊥AB于C,交⊙O于D,
∵CD=4,OD=10,
∴OC=6,
又∵OB=10,
∴Rt△BCO中,BC=,
∴AB=2BC=16.
故选:C.
9.解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=4,
设OF=x,则ON=OF,
∴OM=MN﹣ON=4﹣x,MF=2,
在直角三角形OMF中,OM2+MF2=OF2
即:(4﹣x)2+22=x2
解得:x=2.5
故选:B.
10.解:连接AC,AO,
∵⊙O的直径CD=10cm,AB⊥CD,AB=8cm,
∴AM=AB=×8=4(cm),OD=OC=5(cm),
当C点位置如图1所示时,
∵OA=5cm,AM=4cm,CD⊥AB,
∴OM===3(cm),
∴CM=OC+OM=5+3=8(cm),
∴AC===4(cm);
当C点位置如图2所示时,
同理可得:OM=3cm,
∵OC=5cm,
∴MC=5﹣3=2(cm),
在Rt△AMC中,AC===2(cm);
综上所述,AC的长为4cm或2cm,
故选:C.
二.填空题(共6小题,满分30分)
11.解:如图,作OC⊥AB于C,连接OA,
则AC=BC=AB=5,
在Rt△OAC中,OC==12,
所以圆心O到AB的距离为12cm.
故答案为12.
12.解:连接OA,如图,
∵OC⊥AB,
∴AD=BD=AB=×16=8,
在Rt△OAD中,OD==6,
∴CD=OC﹣OD=10﹣6=4.
故答案为4.
13.解:连接OA,如图,
∵CE=3cm,DE=7cm,
∴CD=10cm,
∴OC=OA=5cm,OE=2cm,
∵AB⊥CD,
∴AE=BE,
在Rt△AOE中,AE==(cm),
∴AB=2AE=2(cm).
故答案为2.
14.解:连接AO,
∵AB=6,OP⊥AB,
∴AP=3,
∵AO=5,
∴OP===4.
故答案为:4.
15.解:∵BD=CD,
∴OD⊥BC,
在Rt△OBD中,∵OB=5,OD=3,
∴BD==4,
∴BC=2BD=8.
故答案为8.
16.解:过点C作CE⊥AB,垂足为E,
∵∠C=90°,AC=5,CB=12,
∴由勾股定理,得AB=13,
∵5×12=13 CE,∴CE=,
∴由勾股定理,得AE=,
∴由垂径定理得AD=.
故答案为.
三.解答题(共8小题,满分50分)
17.解:连接OC,如图,
∵AB是⊙O的直径,AB=10,
∴OC=OA=5,
∵CD⊥AB,
∴CE=DE=CD=×8=4,
在Rt△OCE中,OC=5,CE=4,
∴OE==3,
∴AE=OA﹣OE=5﹣3=2.
18.解:连接AO,如图所示:
∵半径OC⊥弦AB,
∴AD=BD=AB,
∵AB=6,
∴AD=BD=3,
设⊙O的半径为R,
∵CD=1,
∴OD=R﹣1,
在Rt△AOD中,由勾股定理得:OA2=OD2+AD2,
即R2=(R﹣1)2+32,
∴R=5,
即⊙O的半径长为5.
19.解:(1)连接OC,设OC=r,则OE=r﹣1,
∵⊙O的直径AB垂直于弦CD,垂足为E,AE=1,CD=2,
CE=DE=.
在Rt△OCE中,
∵CE2+OE2=OC2,即()2+(r﹣1)2=r2,解得r=2,
∵AB=2r=4;
(2)△BCD是等边三角形.
理由:∵AB=4,AE=1,
∴BE=4﹣1=3,
∴tan∠BCD===,
∴∠BCD=60°.
∵AB⊥CD,
∴∠BDC=∠BCD=60°,
∴△BCD是等边三角形.
20.解:(1)连接OB,
∵AO=OB,OC=BC,
∴∠A=∠B=∠BOC.
∵OA⊥OC,
∴∠AOC=90°.
∵∠A+∠B+∠BOC+∠AOC=180°,
∴3∠A+90°=180°,
∴∠A=30°;
(2)∵∠A=30°,OA=5cm,
∴AC===cm,
BC=OC=AC=cm,
∴AB=AC+BC=+=5(cm).
21.解:如图,连接AC,
∵⊙O的直径AB垂直于弦CD,CD=6cm,
∴CE=DE==3cm,
设AE=x,则BE=10﹣x,
∴CE2=AE BE,
即9=x(10﹣x),
解得:x1=9,x2=1,
∴AE=1,BE=9,
在Rt△BCE中,
CB===3.
22.解:连接OC,
∵E为0B的中点,又OC=OB,
∴OE=OC,
∴∠OCE=30°,
∴∠COE=60°,
又∵OA=OC,
∴∠A=∠OCA=30°,
∴∠ACE=60°.
23.解:过点O作OD⊥AB于点D,连接OA,
∵PA=AB=2,PO=5,
∴AD=1,
∴PD=PA+AD=2+1=3,
∴OD===4,
∴OA===.
答:⊙O的半径是.
一.选择题(共10小题,满分40分)
1.如图,在⊙O中,直径AB=10,弦DE⊥AB于点C,若OC:OB=3:5,连接DO,则DE的长为( )
A.3 B.4 C.6 D.8
2.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=6,CD=4,则AE的长为( )
A. B. C. D.
3.如图,弦CD垂直于⊙O的直径AB,垂足为H,且OB=13,CD=24,则OH的长是( )
A.3 B.4 C.5 D.6
4.AB和CD是⊙O的两条平行弦,AB=6,CD=8,⊙O的半径为5,则AB与CD间的距离为( )
A.1 B.7 C.1或7 D.3或4
5.在半径为50mm的⊙O中,弦AB的长为50mm,则点O到AB的距离为( )
A.50mm B.25mm C.25mm D.25mm
6.在直径为20cm的圆柱形油槽内装入一些油后,截面如图所示,若油槽面宽AB=16cm,则油的最大深度为( )
A.4cm B.6cm C.8cm D.10cm
7.如图,⊙O的弦AB=8,C是AB的中点,且OC=3,OC⊥AB,则⊙O的周长等于( )
A.4π B.5π C.8π D.10π
8.如图,在半径为10cm的圆形铁片上切下一块高为4cm的弓形铁片,则弓形弦AB的长为( )
A.8cm B.12cm C.16cm D.20cm
9.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径长是( )
A.2cm B.2.5cm C.3cm D.4cm
10.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )
A.2cm B.4cm C.2cm或4cm D.2cm或4cm
二.填空题(共6小题,满分30分)
11.已知⊙O的半径为13cm,弦AB的长为10cm,则圆心O到AB的距离为 cm.
12.如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为10,AB=16,则CD的长是 .
13.如图,⊙O的直径CD垂直弦AB于点E,且CE=3cm,DE=7cm,则弦AB= cm.
14.如图,在半径为5的⊙O中,弦AB=6,OP⊥AB,垂足为点P,则OP的长为 .
15.如图,⊙O的半径OA与弦BC交于点D.若OD=3,AD=2,BD=CD,则BC的长为 .
16.如图∠C=90°,⊙C与AB相交于点D,AC=5,CB=12,则AD= .
三.解答题(共8小题,满分50分)
17.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,求线段AE的长.
18.如图,在⊙O中,半径OC⊥弦AB,垂足为点D,AB=6,CD=1,求⊙O半径的长.
19.如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=1,CD=2.
(1)求AB的长;
(2)连接BC和BD,请判断△BCD的形状,并证明.
20.如图,⊙O的半径OA=5cm,AB是弦,C是AB上一点,且OC⊥OA,OC=BC
(1)求∠A的度数.
(2)求AB的长.
21.如图,⊙O的直径AB垂直于弦CD,垂足为E.已知AB=10cm,CD=6cm.求CB的长.
22.如图,AB为⊙O的直径,E为OB的中点,CD为过E点并垂直AB的弦,求∠ACE的度数.
23.如图,P是⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径.
参考答案
一.选择题(共10小题,满分40分)
1.解:∵AB=10,OC:OB=3:5,
∴OC=3,
在Rt△OCD中,CD===4,
∵DE⊥AB,
∴DE=2CD=8,
故选:D.
2.解:连接OC,如图,
∵CD⊥AB,
∴CE=DE=CD=2,
在Rt△OCE中,∵OC=3,CE=2,
∴OE==,
∴AE=OA+OE=3+.
故选:B.
3.解:连接OC,
∵AB是⊙O的直径,CD⊥AB,
∴CH=CD=12,
在Rt△OCH中,OH===5,
故选:C.
4.解:①当AB、CD在圆心两侧时;
过O作OE⊥CD交CD于E点,过O作OF⊥AB交AB于F点,连接OA、OC,如图所示:
∵半径r=5,弦AB∥CD,且AB=6,CD=8,
∴OA=OC=5,CE=DE=4,AF=FB=3,E、F、O在一条直线上,
∴EF为AB、CD之间的距离
在Rt△OEC中,由勾股定理可得:
OE2=OC2﹣CE2
∴OE==3,
在Rt△OFA中,由勾股定理可得:
OF2=OA2﹣AF2
∴OF==4,
∴EF=OE+OF=3+4=7,
AB与CD的距离为7;
②当AB、CD在圆心同侧时;
同①可得:OE=3,OF=4;
则AB与CD的距离为:OF﹣OE=1;
综上所述:AB与CD间的距离为1或7.
故选:C.
5.解:作OC⊥AB于C,
根据题意:OA=OB=AB=50mm,
∴△AOB是等边三角形,
∴∠AOC=30°,
∴OC=OA cos30°=25cm.
故选:B.
6.解:过圆心O向AB作垂线,交AB于点C.
根据勾股定理可得OC==6.
所以油的最大深度为10﹣6=4(cm).
故选:A.
7.解:连接OA,如图,
∵C是AB的中点,
∴AC=BC=AB=4,OC⊥AB,
在Rt△OAC中,OA===5,
∴⊙O的周长=2π×5=10π.
故选:D.
8.解:如图,过O作OD⊥AB于C,交⊙O于D,
∵CD=4,OD=10,
∴OC=6,
又∵OB=10,
∴Rt△BCO中,BC=,
∴AB=2BC=16.
故选:C.
9.解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=4,
设OF=x,则ON=OF,
∴OM=MN﹣ON=4﹣x,MF=2,
在直角三角形OMF中,OM2+MF2=OF2
即:(4﹣x)2+22=x2
解得:x=2.5
故选:B.
10.解:连接AC,AO,
∵⊙O的直径CD=10cm,AB⊥CD,AB=8cm,
∴AM=AB=×8=4(cm),OD=OC=5(cm),
当C点位置如图1所示时,
∵OA=5cm,AM=4cm,CD⊥AB,
∴OM===3(cm),
∴CM=OC+OM=5+3=8(cm),
∴AC===4(cm);
当C点位置如图2所示时,
同理可得:OM=3cm,
∵OC=5cm,
∴MC=5﹣3=2(cm),
在Rt△AMC中,AC===2(cm);
综上所述,AC的长为4cm或2cm,
故选:C.
二.填空题(共6小题,满分30分)
11.解:如图,作OC⊥AB于C,连接OA,
则AC=BC=AB=5,
在Rt△OAC中,OC==12,
所以圆心O到AB的距离为12cm.
故答案为12.
12.解:连接OA,如图,
∵OC⊥AB,
∴AD=BD=AB=×16=8,
在Rt△OAD中,OD==6,
∴CD=OC﹣OD=10﹣6=4.
故答案为4.
13.解:连接OA,如图,
∵CE=3cm,DE=7cm,
∴CD=10cm,
∴OC=OA=5cm,OE=2cm,
∵AB⊥CD,
∴AE=BE,
在Rt△AOE中,AE==(cm),
∴AB=2AE=2(cm).
故答案为2.
14.解:连接AO,
∵AB=6,OP⊥AB,
∴AP=3,
∵AO=5,
∴OP===4.
故答案为:4.
15.解:∵BD=CD,
∴OD⊥BC,
在Rt△OBD中,∵OB=5,OD=3,
∴BD==4,
∴BC=2BD=8.
故答案为8.
16.解:过点C作CE⊥AB,垂足为E,
∵∠C=90°,AC=5,CB=12,
∴由勾股定理,得AB=13,
∵5×12=13 CE,∴CE=,
∴由勾股定理,得AE=,
∴由垂径定理得AD=.
故答案为.
三.解答题(共8小题,满分50分)
17.解:连接OC,如图,
∵AB是⊙O的直径,AB=10,
∴OC=OA=5,
∵CD⊥AB,
∴CE=DE=CD=×8=4,
在Rt△OCE中,OC=5,CE=4,
∴OE==3,
∴AE=OA﹣OE=5﹣3=2.
18.解:连接AO,如图所示:
∵半径OC⊥弦AB,
∴AD=BD=AB,
∵AB=6,
∴AD=BD=3,
设⊙O的半径为R,
∵CD=1,
∴OD=R﹣1,
在Rt△AOD中,由勾股定理得:OA2=OD2+AD2,
即R2=(R﹣1)2+32,
∴R=5,
即⊙O的半径长为5.
19.解:(1)连接OC,设OC=r,则OE=r﹣1,
∵⊙O的直径AB垂直于弦CD,垂足为E,AE=1,CD=2,
CE=DE=.
在Rt△OCE中,
∵CE2+OE2=OC2,即()2+(r﹣1)2=r2,解得r=2,
∵AB=2r=4;
(2)△BCD是等边三角形.
理由:∵AB=4,AE=1,
∴BE=4﹣1=3,
∴tan∠BCD===,
∴∠BCD=60°.
∵AB⊥CD,
∴∠BDC=∠BCD=60°,
∴△BCD是等边三角形.
20.解:(1)连接OB,
∵AO=OB,OC=BC,
∴∠A=∠B=∠BOC.
∵OA⊥OC,
∴∠AOC=90°.
∵∠A+∠B+∠BOC+∠AOC=180°,
∴3∠A+90°=180°,
∴∠A=30°;
(2)∵∠A=30°,OA=5cm,
∴AC===cm,
BC=OC=AC=cm,
∴AB=AC+BC=+=5(cm).
21.解:如图,连接AC,
∵⊙O的直径AB垂直于弦CD,CD=6cm,
∴CE=DE==3cm,
设AE=x,则BE=10﹣x,
∴CE2=AE BE,
即9=x(10﹣x),
解得:x1=9,x2=1,
∴AE=1,BE=9,
在Rt△BCE中,
CB===3.
22.解:连接OC,
∵E为0B的中点,又OC=OB,
∴OE=OC,
∴∠OCE=30°,
∴∠COE=60°,
又∵OA=OC,
∴∠A=∠OCA=30°,
∴∠ACE=60°.
23.解:过点O作OD⊥AB于点D,连接OA,
∵PA=AB=2,PO=5,
∴AD=1,
∴PD=PA+AD=2+1=3,
∴OD===4,
∴OA===.
答:⊙O的半径是.
