2021-2022学年北师大版九年级数学下册 3.7切线长定理 同步达标测评(word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册 3.7切线长定理 同步达标测评(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 298.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 18:27:14 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《3.7切线长定理》同步达标测评(附答案)
一.选择题(共6小题,满分30分)
1.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为( )
A.44 B.42 C.46 D.47
2.如图,一个菱形的边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿此菱形的四边做无滑动旋转,直至回到原出发位置时,这个圆共转了( )
A.6圈 B.5圈 C.4.5圈 D.4圈
3.如图,PA,PB分别切⊙O与点A,B,MN切⊙O于点C,分别交PA,PB于点M,N,若PA=7.5cm,则△PMN的周长是( )
A.7.5cm B.10cm C.12.5cm D.15cm
4.如图,直线AB、CD、BC分别与⊙O相切于E、F、G,且AB∥CD,若OB=6cm,OC=8cm,则BE+CG的长等于( )
A.13 B.12 C.11 D.10
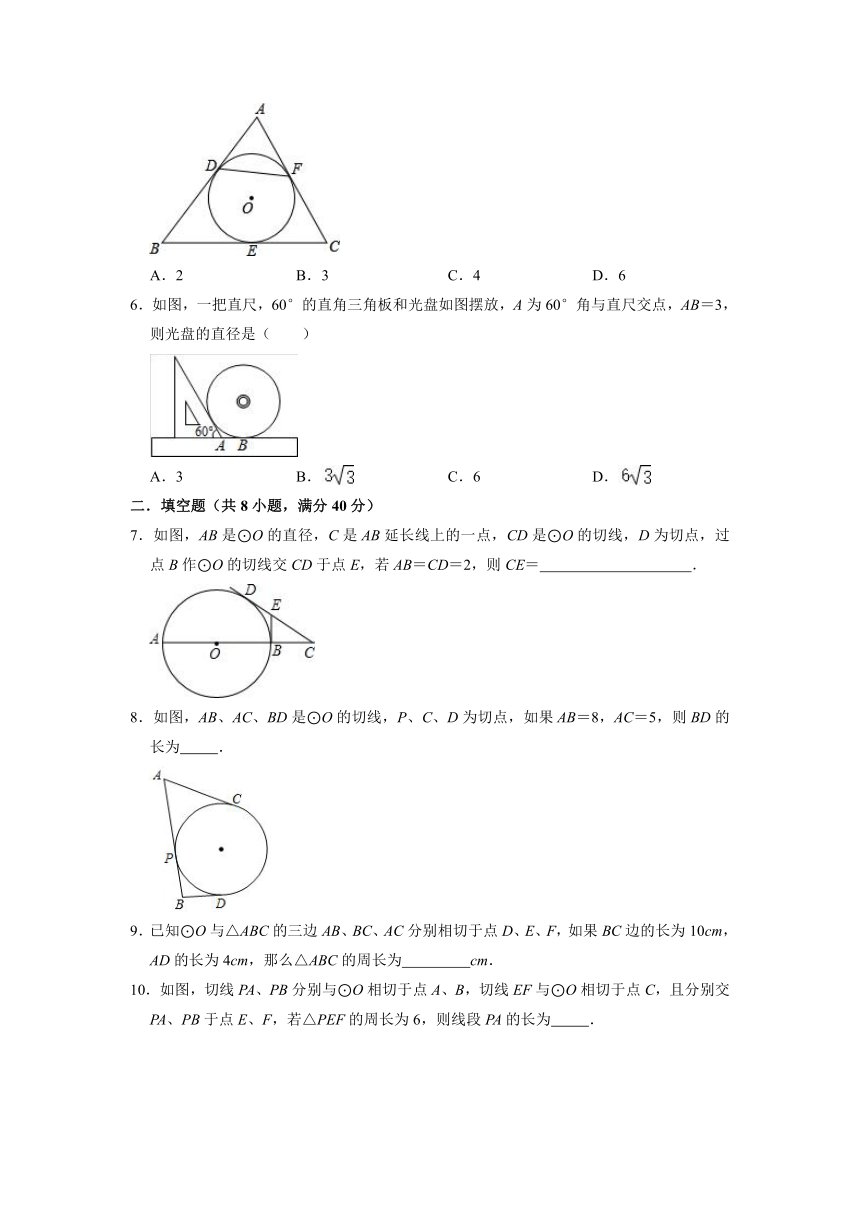
5.如图,△ABC中,∠A=60°,BC=6,它的周长为16.若⊙O与BC,AC,AB三边分别切于E,F,D点,则DF的长为( )
A.2 B.3 C.4 D.6
6.如图,一把直尺,60°的直角三角板和光盘如图摆放,A为60°角与直尺交点,AB=3,则光盘的直径是( )
A.3 B. C.6 D.
二.填空题(共8小题,满分40分)
7.如图,AB是⊙O的直径,C是AB延长线上的一点,CD是⊙O的切线,D为切点,过点B作⊙O的切线交CD于点E,若AB=CD=2,则CE= .
8.如图,AB、AC、BD是⊙O的切线,P、C、D为切点,如果AB=8,AC=5,则BD的长为 .
9.已知⊙O与△ABC的三边AB、BC、AC分别相切于点D、E、F,如果BC边的长为10cm,AD的长为4cm,那么△ABC的周长为 cm.
10.如图,切线PA、PB分别与⊙O相切于点A、B,切线EF与⊙O相切于点C,且分别交PA、PB于点E、F,若△PEF的周长为6,则线段PA的长为 .
11.如图,菱形ABCD,∠B=60°,AB=4,⊙O内切于菱形ABCD,则⊙O的半径为 .
12.如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P= °.
13.如图,PA,PB切⊙O于A、B两点,CD切⊙O于E点,⊙O的半径是r,△PCD周长为4r,则tan∠APB= .
14.如图,PA、PB是⊙O的切线,A、B为切点,点C、D在⊙O上.若∠P=102°,则∠A+∠C= .
三.解答题(共6小题,满分50分)
15.已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.
(1)若PA=6,求△PCD的周长.
(2)若∠P=50°求∠DOC.
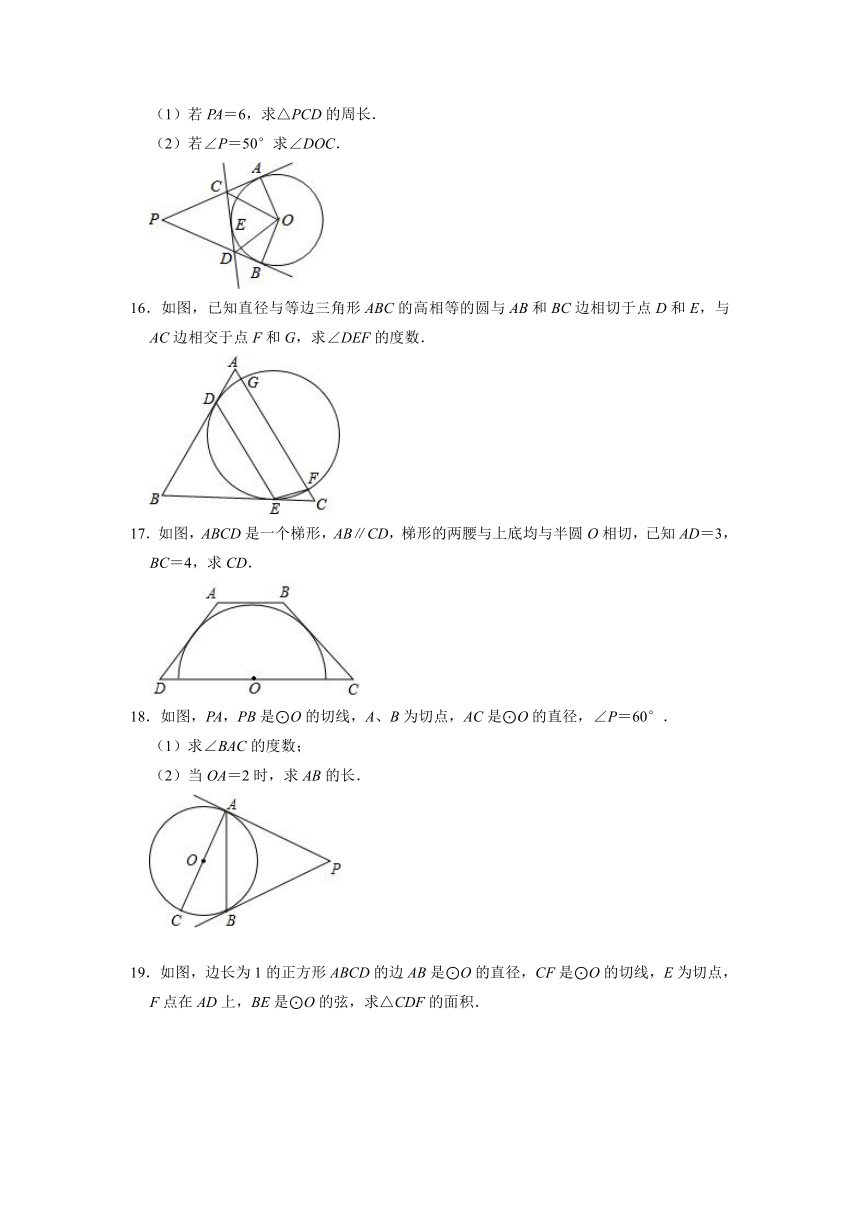
16.如图,已知直径与等边三角形ABC的高相等的圆与AB和BC边相切于点D和E,与AC边相交于点F和G,求∠DEF的度数.
17.如图,ABCD是一个梯形,AB∥CD,梯形的两腰与上底均与半圆O相切,已知AD=3,BC=4,求CD.
18.如图,PA,PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=60°.
(1)求∠BAC的度数;
(2)当OA=2时,求AB的长.
19.如图,边长为1的正方形ABCD的边AB是⊙O的直径,CF是⊙O的切线,E为切点,F点在AD上,BE是⊙O的弦,求△CDF的面积.
20.如图,AB为⊙O直径,PA、PC分别与⊙O相切于点A、C,PQ⊥PA,PQ交OC的延长线于点Q.
(1)求证:OQ=PQ;
(2)连BC并延长交PQ于点D,PA=AB,且CQ=6,求BD的长.
参考答案
一.选择题(共6小题,满分30分)
1.解:∵四边形ABCD是⊙O的外切四边形,
∴AD+BC=AB+CD=22,
∴四边形ABCD的周长=AD+BC+AB+CD=44,
故选:A.
2.解:∵菱形的边长与它的一边相外切的圆的周长相等
∴圆在菱形的边上转了4圈
∵圆在菱形的四个顶点处共转了360°,
∴圆在菱形的四个顶点处共转1圈
∴回到原出发位置时,这个圆共转了5圈.
故选:B.
3.解:∵直线PA、PB、MN分别与⊙O相切于点A、B、C,
∴MA=MC,NC=NB,
∴△PMN的周长=PM+PN+MC+NC=PM+MA+PN+NB=PA+PB=7.5+7.5=15(cm).
故选:D.
4.解:∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵CD、BC,AB分别与⊙O相切于G、F、E,
∴∠OBC=∠ABC,∠OCB=∠BCD,BE=BF,CG=CF,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°,
∴BC==10,
∴BE+CG=10(cm).
故选:D.
5.解:∵⊙O与BC,AC,AB三边分别切于E,F,D点,
∴AD=AF,BE=BD,CE=CF,
∵BC=BE+CE=6,
∴BD+CF=6,
∵AD=AF,∠A=60°,
∴△ADF是等边三角形,
∴AD=AF=DF,
∵AB+AC+BC=16,BC=6,
∴AB+AC=10,
∵BD+CF=6,
∴AD+AF=4,
∵AD=AF=DF,
∴DF=AF=AD=×4=2,
故选:A.
6.解:设三角板与圆的切点为C,连接OA、OB,
由切线长定理知OA平分∠BAC,
∴∠OAB=60°,
在Rt△ABO中,OB=ABtan∠OAB=3,
∴光盘的直径为6,
故选:D.
二.填空题(共8小题,满分40分)
7.解:∵CD是⊙O的切线,∴CD2=CB CA,
∵AB=CD=2,∴4=BC(BC+2),解得BC=﹣1+,
∵CD是⊙O的切线,BE为⊙O的切线,∴∠CBE=∠CDO=90°,
∴△BCE∽△DCO,∴=,
即=,
解得,CE=,
故答案为.
8.解:∵AC、AP为⊙O的切线,
∴AC=AP,
∵BP、BD为⊙O的切线,
∴BP=BD,
∴BD=PB=AB﹣AP=8﹣5=3.
故答案为:3.
9.解:∵⊙O与△ABC的三边AB、BC、AC分别相切于点D、E、F,BC=10cm,AD=4cm,
∴AD=AF=4cm,BE=BD,CF=CE,
即BD+CF=BE+CE=BC=10cm,
∴△ABC的周长是AB+BC+AC=AD+BD+BC+CF+AF=4cm+10cm+10cm+4cm=28cm,
故答案为:28cm.
10.解:∵EA,EC都是圆O的切线,
∴EC=EA,
同理FC=FB,PA=PB,
∴△PEF的周长=PF+PE+EF=PF+PE+EA+FB=PA+PB=2PA=6,
∴PA=3;
故答案为:3.
11.解:设AB和BC上的切点分别为E、F,连接OA、OE、OB、OF,则OE⊥AB,OF⊥BC,
∵⊙O内切于菱形ABCD,
∴OE=OF,
∴OB平分∠ABC,
∵∠ABC=60°,
∴∠ABO=30°,
同理得∠BAO=60°,
∴∠AOB=90°,
∴AO=AB=2,OB=2,
∴S△AOB=AB OE=AO OB,
4OE=2×,
OE=,
故答案为:.
12.解:∵PA,PB是⊙O的切线,
∴PA=PB,PA⊥OA,
∴∠PAB=∠PBA,∠OAP=90°,
∴∠PBA=∠PAB=90°﹣∠OAB=90°﹣38°=52°,
∴∠P=180°﹣52°﹣52°=76°;
故答案为:76.
13.解:连接BO并延长交PA的延长线于F,连接OA,
∵PA,PB切⊙O于A、B两点,CD切⊙O于E点,
∴PA=PB,CE=CA,DE=DB,
∴PA+PB=PC+PD+CD=4r,
∴PA=PB=2r,
∵PA,PB切⊙O于A、B,
∴∠FAO=∠FBP=90°,又∠AFO=∠BFP,
∴△FAO∽△FBP,
∴==,
∴FB=2FA,
∴FA2+r2=(2FA﹣r)2,
解得,FA=r,则FB=r,
∴tan∠APB==,
故答案为:.
14.解:连接AB,
∵PA、PB是⊙O的切线,
∴PA=PB,
∵∠P=102°,
∴∠PAB=∠PBA=(180°﹣102°)=39°,
∵∠DAB+∠C=180°,
∴∠PAD+∠C=∠PAB+∠DAB+∠C=180°+39°=219°,
故答案为:219°.
三.解答题(共6小题,满分50分)
15.解:(1)连接OE,
∵PA、PB与圆O相切,
∴PA=PB=6,
同理可得:AC=CE,BD=DE,
△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PA+PB=12;
(2)∵PA PB与圆O相切,
∴∠OAP=∠OBP=90°∠P=50°,
∴∠AOB=360°﹣90°﹣90°﹣50°=130°,
在Rt△AOC和Rt△EOC中,
,
∴Rt△AOC≌Rt△EOC(HL),
∴∠AOC=∠COE,
同理:∠DOE=∠BOD,
∴∠COD=∠AOB=65°.
16.解:过点E作BC的垂线与圆交于点H,与AC交于点O.
连接AH和DH,作AM⊥BC,垂足为M.
∵E为切点,∴EH必过圆心,即EH是直径,
∴DH⊥DE,
∵D、E是切点,∴BD=BE,
∵∠B=60°,∴△DBE是正三角形,
∴∠BDE=∠BAC=60°,
∴DE∥AC,DH⊥AC,
由已知得,AM=EH,又AM∥EH,∴四边形AMEH是矩形,
∴AH⊥HE,即AH是切线,
∴AD=AH,AC垂直平分DH,AC必过圆心,
∴AC与EH的交点O是圆心,
∴OE=OF,
∵∠COE=90°﹣∠C=30°,∴∠OEF=75°,
∵∠DEO=∠EOC=30°,
∴∠DEF=30°+75°=105°
法二:过点E作BC的垂线与圆交于点H,与AC交于点O.
∵BC为切线
∴O为圆心,OE⊥BC.
∵OE=OF
∴∠OFE=∠OEF.
∴∠OEF=∠C+∠FEC,∠FEC=∠OEF﹣∠C
又∵∠OEC=90°,
∴∠OEF+∠FEC=90°
即2∠OEF﹣∠C=90°.
∵∠C=60°,
∴∠OEF=75°,∠CEF=15°.
又∵AC∥DE,∠C=60°,
∴∠DEC=120°.
∵∠CEF=15°,
∴∠DEF=105°
17.解:如图,连接OE、OA、OF、OB、OG,
∵梯形的两腰与上底均与半圆O相切,
∴OE⊥AD,OF⊥AB,OG⊥BC,
∵AB∥CD,
∴OF是梯形ABCD的高,
∴×AD×OE+×AB×OF+×BC×OG=×(AB+CD)×OF,
∴×(AB+3+4)×OF=×(AB+CD)×OF,
解得,CD=7.
18.解:(1)∵PA,PB是⊙O的切线,
∴AP=BP,
∵∠P=60°,
∴∠PAB=60°,
∵AC是⊙O的直径,
∴∠PAC=90°,
∴∠BAC=90°﹣60°=30°.
(2)连接OP,则在Rt△AOP中,OA=2,∠APO=30°,
∴OP=4,
由勾股定理得:,
∵AP=BP,∠APB=60°,
∴△APB是等边三角形,
∴.
19.解:设AF=x,
∵四边形ABCD是正方形,
∴∠DAB=90°,
∴DA⊥AB,
∴AD是圆的切线,
∵CF是⊙O的切线,E为切点,
∴EF=AF=x,
∴FD=1﹣x,
∵CB⊥AB,
∴CB 为⊙O 的切线,
∴CB=CE,
∴CF=CE+EF=CB+EF=1+x.
∴在Rt△CDF中由勾股定理得到:CF2=CD2+DF2,
即(1+x)2=1+(1﹣x)2,
解得x=,
∴DF=1﹣x=,
∴S△CDF=×1×=.
20.(1)证明:连接OP.
∵PA、PC分别与⊙O相切于点A,C,
∴PA=PC,OA⊥PA,
∵OA=OC,OP=OP,
∴△OPA≌△OPC(SSS),
∴∠AOP=∠POC,
∵QP⊥PA,
∴QP∥BA,
∴∠QPO=∠AOP,
∴∠QOP=∠QPO,
∴OQ=PQ.
(2)设OA=r.
∵OB=OC,
∴∠OBC=∠OCB,
∵OB∥QD,
∴∠QDC=∠B,
∵∠OCB=∠QCD,
∴∠QCD=∠QDC,
∴QC=QD=6,∵QO=QP,
∴OC=DP=r,
∵PC是⊙O的切线,
∴OC⊥PC,
∴∠OCP=∠PCQ=90°,
在Rt△PCQ中,∵PQ2=PC2+QC2,
∴(6+r)2=62+(2r)2,
r=4或0(舍弃),
∴OP==4,
∵OB=PD,OB∥PD,
∴四边形OBDP是平行四边形,
∴BD=OP=4.
一.选择题(共6小题,满分30分)
1.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为( )
A.44 B.42 C.46 D.47
2.如图,一个菱形的边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿此菱形的四边做无滑动旋转,直至回到原出发位置时,这个圆共转了( )
A.6圈 B.5圈 C.4.5圈 D.4圈
3.如图,PA,PB分别切⊙O与点A,B,MN切⊙O于点C,分别交PA,PB于点M,N,若PA=7.5cm,则△PMN的周长是( )
A.7.5cm B.10cm C.12.5cm D.15cm
4.如图,直线AB、CD、BC分别与⊙O相切于E、F、G,且AB∥CD,若OB=6cm,OC=8cm,则BE+CG的长等于( )
A.13 B.12 C.11 D.10
5.如图,△ABC中,∠A=60°,BC=6,它的周长为16.若⊙O与BC,AC,AB三边分别切于E,F,D点,则DF的长为( )
A.2 B.3 C.4 D.6
6.如图,一把直尺,60°的直角三角板和光盘如图摆放,A为60°角与直尺交点,AB=3,则光盘的直径是( )
A.3 B. C.6 D.
二.填空题(共8小题,满分40分)
7.如图,AB是⊙O的直径,C是AB延长线上的一点,CD是⊙O的切线,D为切点,过点B作⊙O的切线交CD于点E,若AB=CD=2,则CE= .
8.如图,AB、AC、BD是⊙O的切线,P、C、D为切点,如果AB=8,AC=5,则BD的长为 .
9.已知⊙O与△ABC的三边AB、BC、AC分别相切于点D、E、F,如果BC边的长为10cm,AD的长为4cm,那么△ABC的周长为 cm.
10.如图,切线PA、PB分别与⊙O相切于点A、B,切线EF与⊙O相切于点C,且分别交PA、PB于点E、F,若△PEF的周长为6,则线段PA的长为 .
11.如图,菱形ABCD,∠B=60°,AB=4,⊙O内切于菱形ABCD,则⊙O的半径为 .
12.如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P= °.
13.如图,PA,PB切⊙O于A、B两点,CD切⊙O于E点,⊙O的半径是r,△PCD周长为4r,则tan∠APB= .
14.如图,PA、PB是⊙O的切线,A、B为切点,点C、D在⊙O上.若∠P=102°,则∠A+∠C= .
三.解答题(共6小题,满分50分)
15.已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.
(1)若PA=6,求△PCD的周长.
(2)若∠P=50°求∠DOC.
16.如图,已知直径与等边三角形ABC的高相等的圆与AB和BC边相切于点D和E,与AC边相交于点F和G,求∠DEF的度数.
17.如图,ABCD是一个梯形,AB∥CD,梯形的两腰与上底均与半圆O相切,已知AD=3,BC=4,求CD.
18.如图,PA,PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=60°.
(1)求∠BAC的度数;
(2)当OA=2时,求AB的长.
19.如图,边长为1的正方形ABCD的边AB是⊙O的直径,CF是⊙O的切线,E为切点,F点在AD上,BE是⊙O的弦,求△CDF的面积.
20.如图,AB为⊙O直径,PA、PC分别与⊙O相切于点A、C,PQ⊥PA,PQ交OC的延长线于点Q.
(1)求证:OQ=PQ;
(2)连BC并延长交PQ于点D,PA=AB,且CQ=6,求BD的长.
参考答案
一.选择题(共6小题,满分30分)
1.解:∵四边形ABCD是⊙O的外切四边形,
∴AD+BC=AB+CD=22,
∴四边形ABCD的周长=AD+BC+AB+CD=44,
故选:A.
2.解:∵菱形的边长与它的一边相外切的圆的周长相等
∴圆在菱形的边上转了4圈
∵圆在菱形的四个顶点处共转了360°,
∴圆在菱形的四个顶点处共转1圈
∴回到原出发位置时,这个圆共转了5圈.
故选:B.
3.解:∵直线PA、PB、MN分别与⊙O相切于点A、B、C,
∴MA=MC,NC=NB,
∴△PMN的周长=PM+PN+MC+NC=PM+MA+PN+NB=PA+PB=7.5+7.5=15(cm).
故选:D.
4.解:∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵CD、BC,AB分别与⊙O相切于G、F、E,
∴∠OBC=∠ABC,∠OCB=∠BCD,BE=BF,CG=CF,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°,
∴BC==10,
∴BE+CG=10(cm).
故选:D.
5.解:∵⊙O与BC,AC,AB三边分别切于E,F,D点,
∴AD=AF,BE=BD,CE=CF,
∵BC=BE+CE=6,
∴BD+CF=6,
∵AD=AF,∠A=60°,
∴△ADF是等边三角形,
∴AD=AF=DF,
∵AB+AC+BC=16,BC=6,
∴AB+AC=10,
∵BD+CF=6,
∴AD+AF=4,
∵AD=AF=DF,
∴DF=AF=AD=×4=2,
故选:A.
6.解:设三角板与圆的切点为C,连接OA、OB,
由切线长定理知OA平分∠BAC,
∴∠OAB=60°,
在Rt△ABO中,OB=ABtan∠OAB=3,
∴光盘的直径为6,
故选:D.
二.填空题(共8小题,满分40分)
7.解:∵CD是⊙O的切线,∴CD2=CB CA,
∵AB=CD=2,∴4=BC(BC+2),解得BC=﹣1+,
∵CD是⊙O的切线,BE为⊙O的切线,∴∠CBE=∠CDO=90°,
∴△BCE∽△DCO,∴=,
即=,
解得,CE=,
故答案为.
8.解:∵AC、AP为⊙O的切线,
∴AC=AP,
∵BP、BD为⊙O的切线,
∴BP=BD,
∴BD=PB=AB﹣AP=8﹣5=3.
故答案为:3.
9.解:∵⊙O与△ABC的三边AB、BC、AC分别相切于点D、E、F,BC=10cm,AD=4cm,
∴AD=AF=4cm,BE=BD,CF=CE,
即BD+CF=BE+CE=BC=10cm,
∴△ABC的周长是AB+BC+AC=AD+BD+BC+CF+AF=4cm+10cm+10cm+4cm=28cm,
故答案为:28cm.
10.解:∵EA,EC都是圆O的切线,
∴EC=EA,
同理FC=FB,PA=PB,
∴△PEF的周长=PF+PE+EF=PF+PE+EA+FB=PA+PB=2PA=6,
∴PA=3;
故答案为:3.
11.解:设AB和BC上的切点分别为E、F,连接OA、OE、OB、OF,则OE⊥AB,OF⊥BC,
∵⊙O内切于菱形ABCD,
∴OE=OF,
∴OB平分∠ABC,
∵∠ABC=60°,
∴∠ABO=30°,
同理得∠BAO=60°,
∴∠AOB=90°,
∴AO=AB=2,OB=2,
∴S△AOB=AB OE=AO OB,
4OE=2×,
OE=,
故答案为:.
12.解:∵PA,PB是⊙O的切线,
∴PA=PB,PA⊥OA,
∴∠PAB=∠PBA,∠OAP=90°,
∴∠PBA=∠PAB=90°﹣∠OAB=90°﹣38°=52°,
∴∠P=180°﹣52°﹣52°=76°;
故答案为:76.
13.解:连接BO并延长交PA的延长线于F,连接OA,
∵PA,PB切⊙O于A、B两点,CD切⊙O于E点,
∴PA=PB,CE=CA,DE=DB,
∴PA+PB=PC+PD+CD=4r,
∴PA=PB=2r,
∵PA,PB切⊙O于A、B,
∴∠FAO=∠FBP=90°,又∠AFO=∠BFP,
∴△FAO∽△FBP,
∴==,
∴FB=2FA,
∴FA2+r2=(2FA﹣r)2,
解得,FA=r,则FB=r,
∴tan∠APB==,
故答案为:.
14.解:连接AB,
∵PA、PB是⊙O的切线,
∴PA=PB,
∵∠P=102°,
∴∠PAB=∠PBA=(180°﹣102°)=39°,
∵∠DAB+∠C=180°,
∴∠PAD+∠C=∠PAB+∠DAB+∠C=180°+39°=219°,
故答案为:219°.
三.解答题(共6小题,满分50分)
15.解:(1)连接OE,
∵PA、PB与圆O相切,
∴PA=PB=6,
同理可得:AC=CE,BD=DE,
△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PA+PB=12;
(2)∵PA PB与圆O相切,
∴∠OAP=∠OBP=90°∠P=50°,
∴∠AOB=360°﹣90°﹣90°﹣50°=130°,
在Rt△AOC和Rt△EOC中,
,
∴Rt△AOC≌Rt△EOC(HL),
∴∠AOC=∠COE,
同理:∠DOE=∠BOD,
∴∠COD=∠AOB=65°.
16.解:过点E作BC的垂线与圆交于点H,与AC交于点O.
连接AH和DH,作AM⊥BC,垂足为M.
∵E为切点,∴EH必过圆心,即EH是直径,
∴DH⊥DE,
∵D、E是切点,∴BD=BE,
∵∠B=60°,∴△DBE是正三角形,
∴∠BDE=∠BAC=60°,
∴DE∥AC,DH⊥AC,
由已知得,AM=EH,又AM∥EH,∴四边形AMEH是矩形,
∴AH⊥HE,即AH是切线,
∴AD=AH,AC垂直平分DH,AC必过圆心,
∴AC与EH的交点O是圆心,
∴OE=OF,
∵∠COE=90°﹣∠C=30°,∴∠OEF=75°,
∵∠DEO=∠EOC=30°,
∴∠DEF=30°+75°=105°
法二:过点E作BC的垂线与圆交于点H,与AC交于点O.
∵BC为切线
∴O为圆心,OE⊥BC.
∵OE=OF
∴∠OFE=∠OEF.
∴∠OEF=∠C+∠FEC,∠FEC=∠OEF﹣∠C
又∵∠OEC=90°,
∴∠OEF+∠FEC=90°
即2∠OEF﹣∠C=90°.
∵∠C=60°,
∴∠OEF=75°,∠CEF=15°.
又∵AC∥DE,∠C=60°,
∴∠DEC=120°.
∵∠CEF=15°,
∴∠DEF=105°
17.解:如图,连接OE、OA、OF、OB、OG,
∵梯形的两腰与上底均与半圆O相切,
∴OE⊥AD,OF⊥AB,OG⊥BC,
∵AB∥CD,
∴OF是梯形ABCD的高,
∴×AD×OE+×AB×OF+×BC×OG=×(AB+CD)×OF,
∴×(AB+3+4)×OF=×(AB+CD)×OF,
解得,CD=7.
18.解:(1)∵PA,PB是⊙O的切线,
∴AP=BP,
∵∠P=60°,
∴∠PAB=60°,
∵AC是⊙O的直径,
∴∠PAC=90°,
∴∠BAC=90°﹣60°=30°.
(2)连接OP,则在Rt△AOP中,OA=2,∠APO=30°,
∴OP=4,
由勾股定理得:,
∵AP=BP,∠APB=60°,
∴△APB是等边三角形,
∴.
19.解:设AF=x,
∵四边形ABCD是正方形,
∴∠DAB=90°,
∴DA⊥AB,
∴AD是圆的切线,
∵CF是⊙O的切线,E为切点,
∴EF=AF=x,
∴FD=1﹣x,
∵CB⊥AB,
∴CB 为⊙O 的切线,
∴CB=CE,
∴CF=CE+EF=CB+EF=1+x.
∴在Rt△CDF中由勾股定理得到:CF2=CD2+DF2,
即(1+x)2=1+(1﹣x)2,
解得x=,
∴DF=1﹣x=,
∴S△CDF=×1×=.
20.(1)证明:连接OP.
∵PA、PC分别与⊙O相切于点A,C,
∴PA=PC,OA⊥PA,
∵OA=OC,OP=OP,
∴△OPA≌△OPC(SSS),
∴∠AOP=∠POC,
∵QP⊥PA,
∴QP∥BA,
∴∠QPO=∠AOP,
∴∠QOP=∠QPO,
∴OQ=PQ.
(2)设OA=r.
∵OB=OC,
∴∠OBC=∠OCB,
∵OB∥QD,
∴∠QDC=∠B,
∵∠OCB=∠QCD,
∴∠QCD=∠QDC,
∴QC=QD=6,∵QO=QP,
∴OC=DP=r,
∵PC是⊙O的切线,
∴OC⊥PC,
∴∠OCP=∠PCQ=90°,
在Rt△PCQ中,∵PQ2=PC2+QC2,
∴(6+r)2=62+(2r)2,
r=4或0(舍弃),
∴OP==4,
∵OB=PD,OB∥PD,
∴四边形OBDP是平行四边形,
∴BD=OP=4.
