2021-2022学年北师大版九年级数学下册3.8圆内接正多边形 同步达标测评(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.8圆内接正多边形 同步达标测评(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 451.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 17:20:46 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学下册《3.8圆内接正多边形》同步达标测评(附答案)
一.选择题(共12小题,满分48分)
1.已知圆的半径是2,则该圆的内接正六边形的面积是( )
A.3 B.9 C.18 D.36
2.如图,⊙O是正五边形ABCDE的外接圆,点P是的一点,则∠CPD的度数是( )
A.30° B.36° C.45° D.72°
3.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为( )
A.cm B.9cm C.cm D.cm
4.如图,△ABC和△DEF分别是⊙O的外切正三角形和内接正三角形,则它们的面积比为( )
A.4 B.2 C. D.
5.如图,正五边形ABCDE内接于⊙O,过点A作⊙O的切线交对角线DB的延长线于点F,则下列结论不成立的是( )
A.AE∥BF B.AF∥CD C.DF=AF D.AB=BF
6.已知等边三角形的内切圆半径,外接圆半径和高的比是( )
A.1:2: B.2:3:4 C.1::2 D.1:2:3
7.一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( )
A.5:4 B.5:2 C.:2 D.:
8.如图,AB、AC分别为⊙O的内接正方形、内接正三边形的边,BC是圆内接正n边形的一边,则n等于( )
A.8 B.10 C.12 D.16
9.如图,用四根长为5cm的铁丝,首尾相接围成一个正方形(接点不固定),要将它的四边按图中的方式向外等距离移动acm,同时添加另外四根长为5cm的铁丝(虚线部分)得到一个新的正八边形,则a的值为( )
A.4cm B.5cm C.5cm D. cm
10.如图,A、B、C、D、E是⊙O上的5等分点,连接AC、CE、EB、BD、DA,得到一个五角星图形和五边形MNFGH.有下列3个结论:①AO⊥BE,②∠CGD=∠COD+∠CAD,③BM=MN=NE.其中正确的结论是( )
A.①② B.①③ C.②③ D.①②③
11.如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A. B. C. D.
12.已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:
将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )
A.1.4 B.1.1 C.0.8 D.0.5
二.填空题(共5小题,满分30分)
13.如图,若干全等正五边形排成环状.图中所示的是前3个五边形,要完成这一圆环还需 个五边形.
14.如图,在边长为2的正六边形ABCDEF中,点P是其对角线BE上一动点,连接PC、PD,则△PCD的周长的最小值是 .
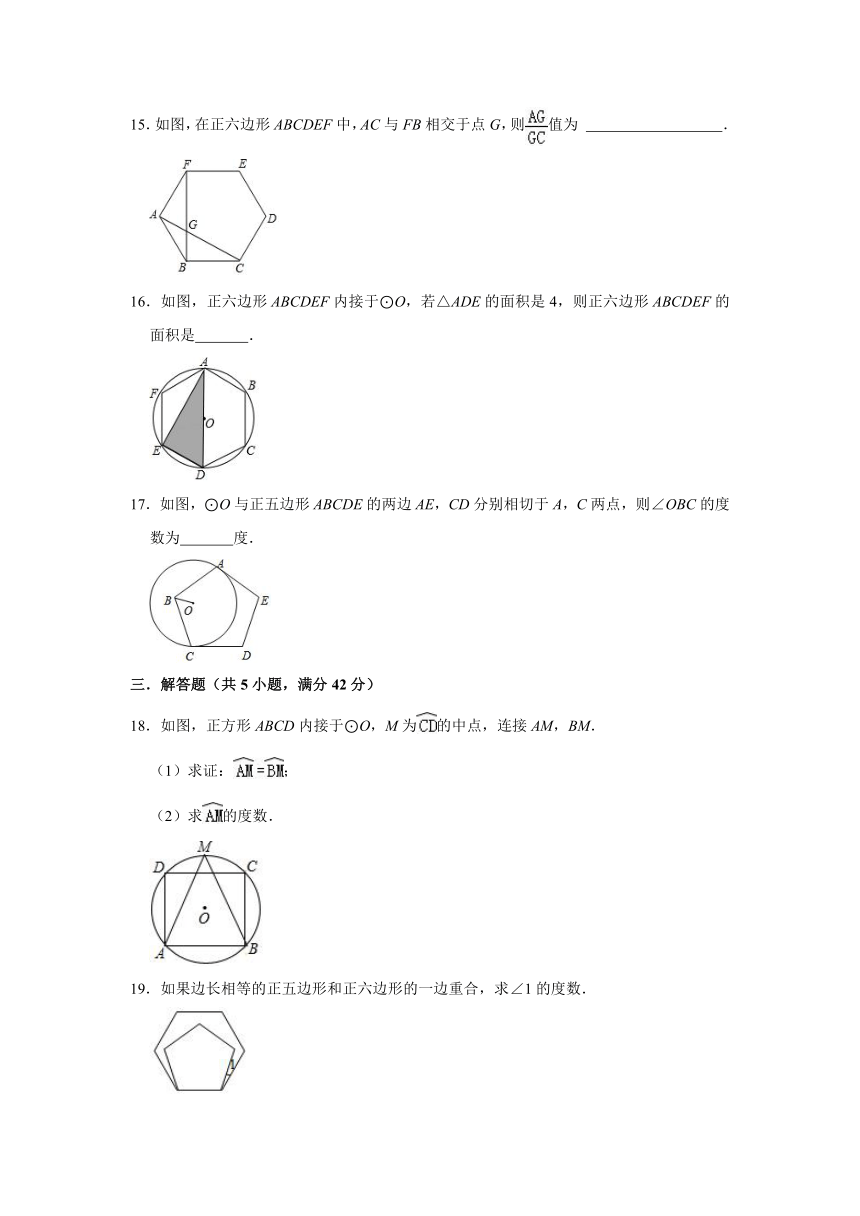
15.如图,在正六边形ABCDEF中,AC与FB相交于点G,则值为 .
16.如图,正六边形ABCDEF内接于⊙O,若△ADE的面积是4,则正六边形ABCDEF的面积是 .
17.如图,⊙O与正五边形ABCDE的两边AE,CD分别相切于A,C两点,则∠OBC的度数为 度.
三.解答题(共5小题,满分42分)
18.如图,正方形ABCD内接于⊙O,M为的中点,连接AM,BM.
(1)求证:;
(2)求的度数.
19.如果边长相等的正五边形和正六边形的一边重合,求∠1的度数.
20.如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=3,EF=4,FC=5,求正方形ABCD的外接圆的半径.
21.如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.
(1)正方形ABCD与正六边形AEFCGH的边长之比为 ;
(2)连接BE,BE是否为⊙O的内接正n边形的一边?如果是,求出n的值;如果不是,请说明理由.
22.在一节数学实践活动课上,老师拿出三个边长都为5cm的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大?问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如下图所示:
(1)通过计算(结果保留根号与π).
(Ⅰ)图①能盖住三个正方形所需的圆形硬纸板最小直径应为 cm;
(Ⅱ)图②能盖住三个正方形所需的圆形硬纸板最小直径为 cm;
(Ⅲ)图③能盖住三个正方形所需的圆形硬纸板最小直径为 cm;
(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法,(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.
参考答案
一.选择题(共12小题,满分48分)
1.解:连接正六边形的中心与各个顶点,得到六个等边三角形,
等边三角形的边长是2,高为3,
因而等边三角形的面积是3,
∴正六边形的面积=18,
故选:C.
2.解:如图,连接OC,OD.
∵ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°,
故选:B.
3.解:如图,圆心为A,设大正方形的边长为2x,圆的半径为R,
根据对称性可知AE=BC=x,CE=2x;
∵小正方形的面积为16cm2,
∴小正方形的边长EF=DF=4,
由勾股定理得,R2=AE2+CE2=AF2+DF2,
即x2+4x2=(x+4)2+42,
解得,x=4或﹣2(舍去),
∴R=cm.
故选:C.
4.解:过点O作ON⊥BC垂足为N,交DE于点M,连接OB,则O,D,B三点一定共线,
设OM=1,则OD=ON=2,
∵∠ODM=∠OBN=30°,
∴OB=4,DM=,DE=2,BN=2,BC=4,
∴S△ABC=×4×6=12,
∴S△DEF=×2×3=3,
∴==4.
故选:A.
5.解:∵五边形ABCDE是正五边形,
∴∠BAE=∠ABC=∠C=∠EDC=∠E==108°,BC=CD,
∴∠CBD=∠CDB=×(180°﹣∠C)=36°,
∴∠ABD=108°﹣36°=72°,
∴∠EAB+∠ABD=180°,
∴AE∥BF,故本选项不符合题意;
B、∵∠F=∠CDB=36°,
∴AF∥CD,故本选项不符合题意;
C、连接AD,过A作AH⊥DF于H,则∠AHF=∠AHD=90°,
∵∠EDC=108°,∠CDB=∠EDA=36°,
∴∠ADF=108°﹣36°﹣36°=36°=∠F,
∴AD=AF,
∴FH=DH,
当∠F=30°时,AF=2AH,FH=DH=AH,
此时DF=AF,
∴此时∠F=36°时,DF≠AF,故本选项符合题意;
D、连接OA、OB,
∵五边形ABCDE是正五边形,
∴∠AOB==72°,
∵OA=OB,
∴∠OAB=∠OBA=(180°﹣72°)=54°,
∵FA切⊙O于A,
∴∠OAF=90°,
∴∠FAB=90°﹣54°=36°,
∵∠ABD=72°,
∴∠F=72°﹣36°=36°=∠FAB,
∴AB=BF,故本选项不符合题意;
故选:C.
6.解:图中内切圆半径是OD,外接圆的半径是OC,高是AD,
因而AD=OC+OD;
在直角△OCD中,∠DOC=60°,
则OD:OC=1:2,
因而OD:OC:AD=1:2:3,
所以内切圆半径,外接圆半径和高的比是1:2:3.故选:D.
7.解:如图1,连接OD,
∵四边形ABCD是正方形,
∴∠DCB=∠ABO=90°,AB=BC=CD=1,
∵∠AOB=45°,
∴OB=AB=1,
由勾股定理得:OD==,
∴扇形的面积是=π;
如图2,连接MB、MC,
∵四边形ABCD是⊙M的内接四边形,四边形ABCD是正方形,
∴∠BMC=90°,MB=MC,
∴∠MCB=∠MBC=45°,
∵BC=1,
∴MC=MB=,
∴⊙M的面积是π×()2=π,
∴扇形和圆形纸板的面积比是π÷(π)=.
故选:A.
8.解:连接AO,BO,CO.
∵AB、AC分别为⊙O的内接正方形、内接正三边形的一边,
∴∠AOB==90°,∠AOC==120°,
∴∠BOC=30°,
∴n==12,
故选:C.
9.解:如图,由题意可知:△ABC是等腰直角三角形,AB=5,AC=BC=a.
则有:a2+a2=52,
∴a=或﹣(舍弃)
故选:D.
10.解:∵A、B、C、D、E是⊙O上的5等分点,
∴=,
∴AO⊥BE,故①正确;
∵A、B、C、D、E是⊙O上的5等分点,
∴的度数==72°,
∴∠COD=72°,
∵∠COD=2∠CAD,
∴∠CAD=36°;
连接CD
∵A、B、C、D、E是⊙O上的5等分点,
∴===,
∴∠BDC=∠DCE=∠CAD=36°,
∴∠CGD=108°,
∴∠CGD=∠COD+∠CAD,故②正确;
连接AB,AE,
∴∠MBA=∠MAB=36°,
∴AM=BM,
∵∠MAN=36°,∠ANM=∠DAE+∠AEB=72°,
∴AM≠MN,
∴BM≠MN③错误!则∠BAM=∠ABM=∠EAN=∠AEN=36°,
∵AB=AE,
∴△ABM≌△AEN(ASA),
∴BM=EN=AM=AN,
∵∠MAN=36°,
∴AM≠MN,∴③错误.
故选:A.
11.解:连接OE1,OD1,OD2,如图,
∵六边形A1B1C1D1E1F1为正六边形,
∴∠E1OD1=60°,
∴△E1OD1为等边三角形,
∵正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,
∴OD2⊥E1D1,
∴OD2=E1D1=×2,
∴正六边形A2B2C2D2E2F2的边长=×2,
同理可得正六边形A3B3C3D3E3F3的边长=()2×2,
则正六边形A10B10C10D10E10F10的边长=()9×2=.
故选:D.
12.解:如图,在这样连续6次旋转的过程中,点M的运动轨迹是图中的红线,
观察图象可知点B,M间的距离大于等于2﹣小于等于1,
故选:C.
二.填空题(共5小题,满分30分)
13.解:延长正五边形的相邻两边,交于圆心,
∵正五边形的外角等于360°÷5=72°,
∴延长正五边形的相邻两边围成的角的度数为:180°﹣72°﹣72°=36°,
∴360°÷36°=10,
∴排成圆环需要10个正五边形,
故 排成圆环还需 7个五边形.
故答案为:7.
14.解:要使△PCD的周长的最小,即PC+PD最小.
利用正多边形的性质可得点C关于BE的对称点为点A,连接AD交BE于点P',那么有P'C=P'A,P'C+P'D=AD最小.
又易知ABCD为等腰梯形,∠BAD=∠CDA=60°,
则作BM⊥AD于点M,CN⊥AD于点N,
∵AB=2,
∴AM=AB=1,
∴AM=DN=1,从而AD=4,
故△PCD的周长的最小值为6.
故答案为:6.
15.解:∵六边形ABCDEF是正六边形,
∴AB=BC=AF,∠ABC=∠BAF=120°,
∴∠ABF=∠BAC=∠BCA=30°,
∴AG=BG,∠CBG=90°,
∴CG=2BG=2AG,
∴=;
故答案为:.
16.解:∵六边形ABCDEF是正六边形,
∴∠DEF=∠BAF=∠F=120°,∠DAF=60°,DE=AF=EF,
∴∠AEF=∠EAF=30°,,
∴∠DAE=∠EAF=30°,∠AED=90°,
∴AD为直径,DE=AD=OD=OE,
∴△ODE是等边三角形,
∵△ADE的面积是4,
∴△ODE的面积=△ADE的面积=2,
∴正六边形ABCDEF的面积=6△ODE的面积=6×2=12;
故答案为:12.
17.解:连接OA,OC.
∵BA=BC,BO=BO,OA=OC,
∴△ABO≌△CBO(SSS),
∴∠ABO=∠CBO,
∵∠ABC=108°,
∴∠OBC=∠ABC=54°,
故答案为54.
三.解答题(共5小题,满分42分)
18.(1)证明:∵四边形ABCD是正方形,
∴AD=BC,
∴=,
∵M为的中点,
∴=,
∴+=+,
∴;
(2)解:连接OM,OA,OB,
∵正方形ABCD内接于⊙O,
∴∠AOB=90°,
∴∠AOM=∠BOM=(360°﹣90°)=135°,
∴的度数是135°.
19.解:正五边形的内角=108°,正六边形的内角=120°,
故∠1=120°﹣108°=12°.
20.解:连接AC,则AC是该圆的直径,延长AE交圆于G,
连接CG,则∠AGC=90°,
∵AE⊥EF,EF⊥FC,
∵四边形EFCG是矩形,
∴EG=FC=5,GC=EF=4,
∴AG=8.
由勾股定理得,AC==4,
∴正方形外接圆的半径为2.
21.解:(1)设此圆的半径为R,
则它的内接正方形的边长为R,
它的内接正六边形的边长为R,
内接正方形和内接正六边形的边长比为R:R=:1.
故答案为::1;
(2)BE是⊙O的内接正十二边形的一边,
理由:连接OA,OB,OE,
在正方形ABCD中,∠AOB=90°,
在正六边形AEFCGH中,∠AOE=60°,
∴∠BOE=30°,
∵n==12,
∴BE是正十二边形的边.
22.解:(1)(Ⅰ)连接BD,
∵AD=3×5=15cm,AB=5cm,
∴BD==cm;
(Ⅱ)如图所示,
∵三个正方形的边长均为5,
∴A、B、C三点在以O为圆心,以OA为半径的圆上,
∴OA==5cm,
∴能盖住三个正方形所需的圆形硬纸板最小直径为10cm;
(Ⅲ)如图所示,
∵CE⊥AB,AC=BC,
∴AD是过A、B、C三点的圆的直径,
∵OA=OB=OD,
∴O为圆心,
∴⊙O的半径为OA,
OA==5cm,
∴能盖住三个正方形所需的圆形硬纸板最小直径为5×2=10cm;
(2)如图④为盖住三个正方形时直径最小的放置方法,
连接OB,ON,延长OH交AB于点P,则OP⊥AB,P为AB中点,
设OG=x,则OP=10﹣x,
则有:,
解得:,(8分)
则ON=,
∴直径为.
一.选择题(共12小题,满分48分)
1.已知圆的半径是2,则该圆的内接正六边形的面积是( )
A.3 B.9 C.18 D.36
2.如图,⊙O是正五边形ABCDE的外接圆,点P是的一点,则∠CPD的度数是( )
A.30° B.36° C.45° D.72°
3.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为( )
A.cm B.9cm C.cm D.cm
4.如图,△ABC和△DEF分别是⊙O的外切正三角形和内接正三角形,则它们的面积比为( )
A.4 B.2 C. D.
5.如图,正五边形ABCDE内接于⊙O,过点A作⊙O的切线交对角线DB的延长线于点F,则下列结论不成立的是( )
A.AE∥BF B.AF∥CD C.DF=AF D.AB=BF
6.已知等边三角形的内切圆半径,外接圆半径和高的比是( )
A.1:2: B.2:3:4 C.1::2 D.1:2:3
7.一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( )
A.5:4 B.5:2 C.:2 D.:
8.如图,AB、AC分别为⊙O的内接正方形、内接正三边形的边,BC是圆内接正n边形的一边,则n等于( )
A.8 B.10 C.12 D.16
9.如图,用四根长为5cm的铁丝,首尾相接围成一个正方形(接点不固定),要将它的四边按图中的方式向外等距离移动acm,同时添加另外四根长为5cm的铁丝(虚线部分)得到一个新的正八边形,则a的值为( )
A.4cm B.5cm C.5cm D. cm
10.如图,A、B、C、D、E是⊙O上的5等分点,连接AC、CE、EB、BD、DA,得到一个五角星图形和五边形MNFGH.有下列3个结论:①AO⊥BE,②∠CGD=∠COD+∠CAD,③BM=MN=NE.其中正确的结论是( )
A.①② B.①③ C.②③ D.①②③
11.如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A. B. C. D.
12.已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:
将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )
A.1.4 B.1.1 C.0.8 D.0.5
二.填空题(共5小题,满分30分)
13.如图,若干全等正五边形排成环状.图中所示的是前3个五边形,要完成这一圆环还需 个五边形.
14.如图,在边长为2的正六边形ABCDEF中,点P是其对角线BE上一动点,连接PC、PD,则△PCD的周长的最小值是 .
15.如图,在正六边形ABCDEF中,AC与FB相交于点G,则值为 .
16.如图,正六边形ABCDEF内接于⊙O,若△ADE的面积是4,则正六边形ABCDEF的面积是 .
17.如图,⊙O与正五边形ABCDE的两边AE,CD分别相切于A,C两点,则∠OBC的度数为 度.
三.解答题(共5小题,满分42分)
18.如图,正方形ABCD内接于⊙O,M为的中点,连接AM,BM.
(1)求证:;
(2)求的度数.
19.如果边长相等的正五边形和正六边形的一边重合,求∠1的度数.
20.如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=3,EF=4,FC=5,求正方形ABCD的外接圆的半径.
21.如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.
(1)正方形ABCD与正六边形AEFCGH的边长之比为 ;
(2)连接BE,BE是否为⊙O的内接正n边形的一边?如果是,求出n的值;如果不是,请说明理由.
22.在一节数学实践活动课上,老师拿出三个边长都为5cm的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大?问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如下图所示:
(1)通过计算(结果保留根号与π).
(Ⅰ)图①能盖住三个正方形所需的圆形硬纸板最小直径应为 cm;
(Ⅱ)图②能盖住三个正方形所需的圆形硬纸板最小直径为 cm;
(Ⅲ)图③能盖住三个正方形所需的圆形硬纸板最小直径为 cm;
(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法,(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.
参考答案
一.选择题(共12小题,满分48分)
1.解:连接正六边形的中心与各个顶点,得到六个等边三角形,
等边三角形的边长是2,高为3,
因而等边三角形的面积是3,
∴正六边形的面积=18,
故选:C.
2.解:如图,连接OC,OD.
∵ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°,
故选:B.
3.解:如图,圆心为A,设大正方形的边长为2x,圆的半径为R,
根据对称性可知AE=BC=x,CE=2x;
∵小正方形的面积为16cm2,
∴小正方形的边长EF=DF=4,
由勾股定理得,R2=AE2+CE2=AF2+DF2,
即x2+4x2=(x+4)2+42,
解得,x=4或﹣2(舍去),
∴R=cm.
故选:C.
4.解:过点O作ON⊥BC垂足为N,交DE于点M,连接OB,则O,D,B三点一定共线,
设OM=1,则OD=ON=2,
∵∠ODM=∠OBN=30°,
∴OB=4,DM=,DE=2,BN=2,BC=4,
∴S△ABC=×4×6=12,
∴S△DEF=×2×3=3,
∴==4.
故选:A.
5.解:∵五边形ABCDE是正五边形,
∴∠BAE=∠ABC=∠C=∠EDC=∠E==108°,BC=CD,
∴∠CBD=∠CDB=×(180°﹣∠C)=36°,
∴∠ABD=108°﹣36°=72°,
∴∠EAB+∠ABD=180°,
∴AE∥BF,故本选项不符合题意;
B、∵∠F=∠CDB=36°,
∴AF∥CD,故本选项不符合题意;
C、连接AD,过A作AH⊥DF于H,则∠AHF=∠AHD=90°,
∵∠EDC=108°,∠CDB=∠EDA=36°,
∴∠ADF=108°﹣36°﹣36°=36°=∠F,
∴AD=AF,
∴FH=DH,
当∠F=30°时,AF=2AH,FH=DH=AH,
此时DF=AF,
∴此时∠F=36°时,DF≠AF,故本选项符合题意;
D、连接OA、OB,
∵五边形ABCDE是正五边形,
∴∠AOB==72°,
∵OA=OB,
∴∠OAB=∠OBA=(180°﹣72°)=54°,
∵FA切⊙O于A,
∴∠OAF=90°,
∴∠FAB=90°﹣54°=36°,
∵∠ABD=72°,
∴∠F=72°﹣36°=36°=∠FAB,
∴AB=BF,故本选项不符合题意;
故选:C.
6.解:图中内切圆半径是OD,外接圆的半径是OC,高是AD,
因而AD=OC+OD;
在直角△OCD中,∠DOC=60°,
则OD:OC=1:2,
因而OD:OC:AD=1:2:3,
所以内切圆半径,外接圆半径和高的比是1:2:3.故选:D.
7.解:如图1,连接OD,
∵四边形ABCD是正方形,
∴∠DCB=∠ABO=90°,AB=BC=CD=1,
∵∠AOB=45°,
∴OB=AB=1,
由勾股定理得:OD==,
∴扇形的面积是=π;
如图2,连接MB、MC,
∵四边形ABCD是⊙M的内接四边形,四边形ABCD是正方形,
∴∠BMC=90°,MB=MC,
∴∠MCB=∠MBC=45°,
∵BC=1,
∴MC=MB=,
∴⊙M的面积是π×()2=π,
∴扇形和圆形纸板的面积比是π÷(π)=.
故选:A.
8.解:连接AO,BO,CO.
∵AB、AC分别为⊙O的内接正方形、内接正三边形的一边,
∴∠AOB==90°,∠AOC==120°,
∴∠BOC=30°,
∴n==12,
故选:C.
9.解:如图,由题意可知:△ABC是等腰直角三角形,AB=5,AC=BC=a.
则有:a2+a2=52,
∴a=或﹣(舍弃)
故选:D.
10.解:∵A、B、C、D、E是⊙O上的5等分点,
∴=,
∴AO⊥BE,故①正确;
∵A、B、C、D、E是⊙O上的5等分点,
∴的度数==72°,
∴∠COD=72°,
∵∠COD=2∠CAD,
∴∠CAD=36°;
连接CD
∵A、B、C、D、E是⊙O上的5等分点,
∴===,
∴∠BDC=∠DCE=∠CAD=36°,
∴∠CGD=108°,
∴∠CGD=∠COD+∠CAD,故②正确;
连接AB,AE,
∴∠MBA=∠MAB=36°,
∴AM=BM,
∵∠MAN=36°,∠ANM=∠DAE+∠AEB=72°,
∴AM≠MN,
∴BM≠MN③错误!则∠BAM=∠ABM=∠EAN=∠AEN=36°,
∵AB=AE,
∴△ABM≌△AEN(ASA),
∴BM=EN=AM=AN,
∵∠MAN=36°,
∴AM≠MN,∴③错误.
故选:A.
11.解:连接OE1,OD1,OD2,如图,
∵六边形A1B1C1D1E1F1为正六边形,
∴∠E1OD1=60°,
∴△E1OD1为等边三角形,
∵正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,
∴OD2⊥E1D1,
∴OD2=E1D1=×2,
∴正六边形A2B2C2D2E2F2的边长=×2,
同理可得正六边形A3B3C3D3E3F3的边长=()2×2,
则正六边形A10B10C10D10E10F10的边长=()9×2=.
故选:D.
12.解:如图,在这样连续6次旋转的过程中,点M的运动轨迹是图中的红线,
观察图象可知点B,M间的距离大于等于2﹣小于等于1,
故选:C.
二.填空题(共5小题,满分30分)
13.解:延长正五边形的相邻两边,交于圆心,
∵正五边形的外角等于360°÷5=72°,
∴延长正五边形的相邻两边围成的角的度数为:180°﹣72°﹣72°=36°,
∴360°÷36°=10,
∴排成圆环需要10个正五边形,
故 排成圆环还需 7个五边形.
故答案为:7.
14.解:要使△PCD的周长的最小,即PC+PD最小.
利用正多边形的性质可得点C关于BE的对称点为点A,连接AD交BE于点P',那么有P'C=P'A,P'C+P'D=AD最小.
又易知ABCD为等腰梯形,∠BAD=∠CDA=60°,
则作BM⊥AD于点M,CN⊥AD于点N,
∵AB=2,
∴AM=AB=1,
∴AM=DN=1,从而AD=4,
故△PCD的周长的最小值为6.
故答案为:6.
15.解:∵六边形ABCDEF是正六边形,
∴AB=BC=AF,∠ABC=∠BAF=120°,
∴∠ABF=∠BAC=∠BCA=30°,
∴AG=BG,∠CBG=90°,
∴CG=2BG=2AG,
∴=;
故答案为:.
16.解:∵六边形ABCDEF是正六边形,
∴∠DEF=∠BAF=∠F=120°,∠DAF=60°,DE=AF=EF,
∴∠AEF=∠EAF=30°,,
∴∠DAE=∠EAF=30°,∠AED=90°,
∴AD为直径,DE=AD=OD=OE,
∴△ODE是等边三角形,
∵△ADE的面积是4,
∴△ODE的面积=△ADE的面积=2,
∴正六边形ABCDEF的面积=6△ODE的面积=6×2=12;
故答案为:12.
17.解:连接OA,OC.
∵BA=BC,BO=BO,OA=OC,
∴△ABO≌△CBO(SSS),
∴∠ABO=∠CBO,
∵∠ABC=108°,
∴∠OBC=∠ABC=54°,
故答案为54.
三.解答题(共5小题,满分42分)
18.(1)证明:∵四边形ABCD是正方形,
∴AD=BC,
∴=,
∵M为的中点,
∴=,
∴+=+,
∴;
(2)解:连接OM,OA,OB,
∵正方形ABCD内接于⊙O,
∴∠AOB=90°,
∴∠AOM=∠BOM=(360°﹣90°)=135°,
∴的度数是135°.
19.解:正五边形的内角=108°,正六边形的内角=120°,
故∠1=120°﹣108°=12°.
20.解:连接AC,则AC是该圆的直径,延长AE交圆于G,
连接CG,则∠AGC=90°,
∵AE⊥EF,EF⊥FC,
∵四边形EFCG是矩形,
∴EG=FC=5,GC=EF=4,
∴AG=8.
由勾股定理得,AC==4,
∴正方形外接圆的半径为2.
21.解:(1)设此圆的半径为R,
则它的内接正方形的边长为R,
它的内接正六边形的边长为R,
内接正方形和内接正六边形的边长比为R:R=:1.
故答案为::1;
(2)BE是⊙O的内接正十二边形的一边,
理由:连接OA,OB,OE,
在正方形ABCD中,∠AOB=90°,
在正六边形AEFCGH中,∠AOE=60°,
∴∠BOE=30°,
∵n==12,
∴BE是正十二边形的边.
22.解:(1)(Ⅰ)连接BD,
∵AD=3×5=15cm,AB=5cm,
∴BD==cm;
(Ⅱ)如图所示,
∵三个正方形的边长均为5,
∴A、B、C三点在以O为圆心,以OA为半径的圆上,
∴OA==5cm,
∴能盖住三个正方形所需的圆形硬纸板最小直径为10cm;
(Ⅲ)如图所示,
∵CE⊥AB,AC=BC,
∴AD是过A、B、C三点的圆的直径,
∵OA=OB=OD,
∴O为圆心,
∴⊙O的半径为OA,
OA==5cm,
∴能盖住三个正方形所需的圆形硬纸板最小直径为5×2=10cm;
(2)如图④为盖住三个正方形时直径最小的放置方法,
连接OB,ON,延长OH交AB于点P,则OP⊥AB,P为AB中点,
设OG=x,则OP=10﹣x,
则有:,
解得:,(8分)
则ON=,
∴直径为.
