2021-2022学年北师大版九年级数学下册 3.9弧长及扇形面积 填空专题练习(word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册 3.9弧长及扇形面积 填空专题练习(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 204.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 18:28:47 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《3.9弧长及扇形面积》填空专题练习(附答案)
1.若一个扇形的圆心角为90°,半径是6,则它的弧长为 .
2.已知钟面上的分针长9厘米,那么分针针尖经过20分钟滑过的弧线长为 厘米.(结果保留π)
3.已知四边形ABCD是⊙O的内接四边形,⊙O半径是2,∠B=120°,则的长是 .
4.如图,⊙O的半径为1,四边形ABCD内接于⊙O,连接OB,OD,若∠BOD=∠BCD,则的长为 .
5.已知扇形的半径为10,弧长为10π,那么这个扇形的圆心角为 度.
6.一个扇形的半径为6,圆心角为120°,则该扇形的面积是 .
7.一个扇形的面积是12πcm2,圆心角是60°,则此扇形的半径是 cm.
8.已知圆心角为120°的扇形的面积为12πcm2,则扇形的弧长是 cm.
9.一个扇形的半径是6cm,弧长是5πcm,则此扇形的面积是 cm2.
10.若一个扇形的面积20,半径为8,则此扇形的弧长为 .
11.为庆祝祖国华诞,某单位排练的节目需用到如图所示的扇形布扇,布扇完全打开后,外侧两竹条AB,AC夹角为120°,AB的长为30cm,贴布部分BD的长为20cm,则贴布部分的面积约为 cm2.
12.如图,扇形AOB的圆心角是为90°,四边形OCDE是边长为1的正方形,点C,E分别在OA,OB,D在弧AB上,那么图中阴影部分的面积为 .(结果保留π)
13.如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为 .
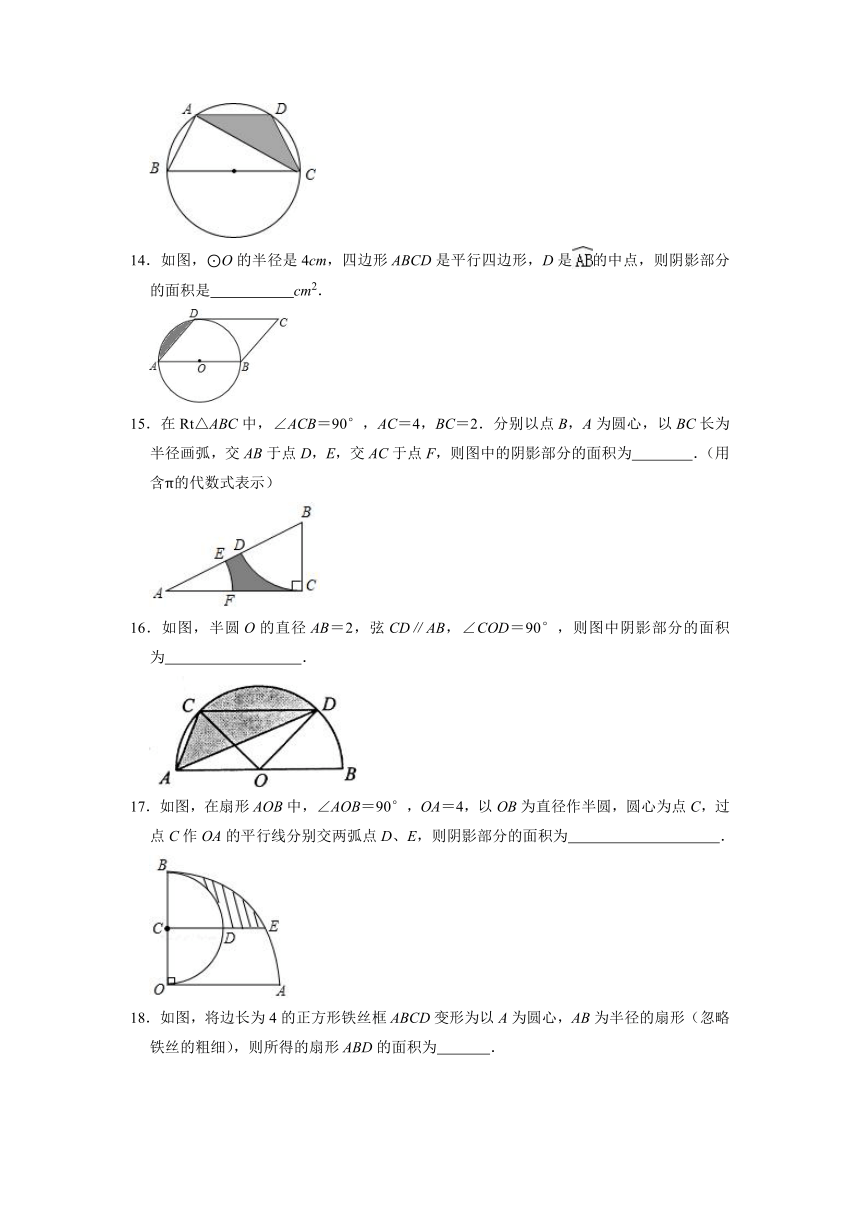
14.如图,⊙O的半径是4cm,四边形ABCD是平行四边形,D是的中点,则阴影部分的面积是 cm2.
15.在Rt△ABC中,∠ACB=90°,AC=4,BC=2.分别以点B,A为圆心,以BC长为半径画弧,交AB于点D,E,交AC于点F,则图中的阴影部分的面积为 .(用含π的代数式表示)
16.如图,半圆O的直径AB=2,弦CD∥AB,∠COD=90°,则图中阴影部分的面积为 .
17.如图,在扇形AOB中,∠AOB=90°,OA=4,以OB为直径作半圆,圆心为点C,过点C作OA的平行线分别交两弧点D、E,则阴影部分的面积为 .
18.如图,将边长为4的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD的面积为 .
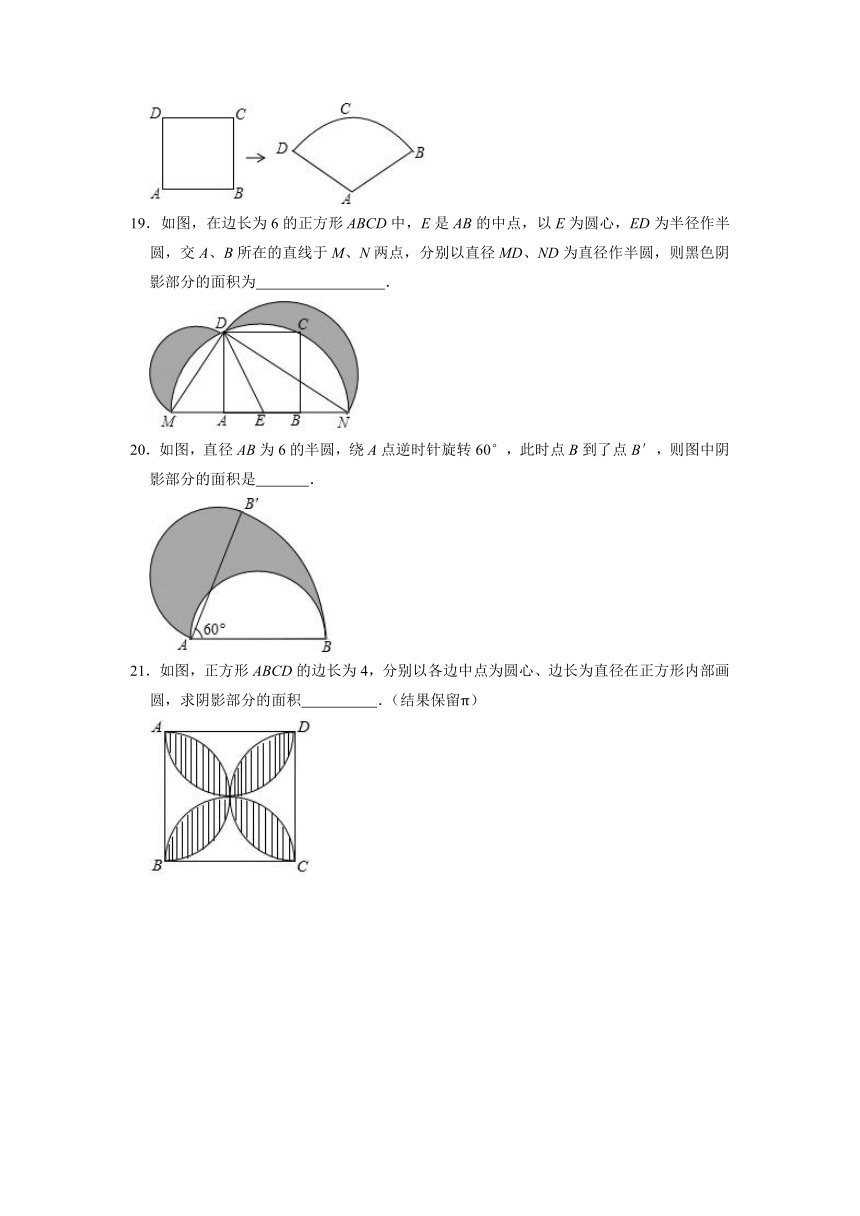
19.如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则黑色阴影部分的面积为 .
20.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是 .
21.如图,正方形ABCD的边长为4,分别以各边中点为圆心、边长为直径在正方形内部画圆,求阴影部分的面积 .(结果保留π)
参考答案
1.解:该扇形的弧长==3π.
故答案为:3π.
2.解:由题意可得,分针针尖经过20分钟滑过的弧线长为:=6π(厘米).
故答案为:6π.
3.解:如图,连接OC,OA.
∵∠B+∠D=180°,∠B=120°,
∴∠D=60°,
∴∠AOC=2∠D=120°,
∴的长==π,
故答案为:π.
4.解:由圆周角定理得,2∠BAD=∠BOD,
∵四边形ABCD是⊙O的内接四边形,
∴∠BCD=180°﹣∠BAD,
∴180°﹣∠BAD=2∠BAD,
解得,∠BAD=60°,
∴∠BOD=2∠BAD=120°,
∴的长==π,
故答案为:π.
5.解:由题意可得,
10π=,
解得n=180,
即这个扇形的圆心角为180°,
故答案为:180.
6.解:∵一个扇形的半径为6,圆心角为120°,
∴该扇形的面积是:=12π,
故答案为:12π.
7.解:设这个扇形的半径是rcm.
根据扇形面积公式,得=12π,
解得r=±6(负值舍去).
故答案为6.
8.解:令扇形的半径和弧长分别为R和l,则
∵S==12π,
∴R=6cm,
∴l==4πcm.
∴扇形的弧长为4πcm.
9.解:根据题意得,S扇形=lR==15π(cm2).
故答案为15π.
10.解:∵一个扇形的面积20,半径为8,
∴此扇形的弧长为:=5,
故答案为:5.
11.解:贴布部分的面积=S扇形BAC﹣S扇形DAE
=﹣
=(cm2).
故答案为.
12.解:∵四边形OCDE是边长为1的正方形,
∴OD=,
∴图中阴影部分的面积=S扇形AOB﹣S正方形OCDE
=﹣1
=π﹣1.
故答案为π﹣1.
13.解:设圆心为O,连接OA、OD.
∵AD∥BC,AC平分∠BCD,∠ADC=120°,
∴∠BCD=60°,
∵AC平分∠BCD,
∴∠ACD=30°,
∴∠AOD=2∠ACD=60°,∠OAC=∠ACO=30°.
∴∠BAC=90°,
∴∠ABC=60°,
又∵OA=OD=OB=OC,
则△AOD、△AOB、△COD都是等边三角形.
∴AB=AD=CD.
又∵四边形ABCD的周长为10cm,
∴OB=OC=AB=AD=DC=2(cm).
∴阴影部分的面积=S梯形﹣S△ABC=(2+4)×﹣×4×=3﹣2=.
故答案为.
14.解:连接OD,
∵D是弧AB的中点
∴∠DOA=∠DOB=90°,
∵OA=OD=4cm,
∴△OAD的面积为OA OD=8cm2,
扇形OAD的面积为:=4π,
∴阴影部分面积为:(4π﹣8)cm2.
故答案为:(4π﹣8).
15.解:∵∠ACB=90°,
∴∠A+∠B=90°,
∴S扇形EAF+S扇形DBC==π,
∴图中的阴影部分的面积=S△ABC﹣(S扇形EAF+S扇形DBC)
=×4×2﹣π
=4﹣π.
故答案为4﹣π.
16.解:∵弦CD∥AB,
∴S△ACD=S△OCD,
∴S阴影=S扇形COD= π =×π×=.
故答案为:.
17.解:连接OE,如图,
∵CE∥OA,
∴∠BCE=90°,
∵OE=4,OC=2,
∴CE=OC=2,
∴∠CEO=30°,∠BOE=60°,
∴S阴影部分=S扇形BOE﹣S△OCE﹣S扇形BCD=﹣×2×2﹣=π﹣2.
故答案为π﹣2
18.解:∵边长为4的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形,
∴的长度为8,
∴所得的扇形ABD的面积=×4×8=16.
故答案为:16.
19.解:根据图形可知阴影部分的面积=两个小的半圆的面积+△DMN的面积﹣大半圆的面积.
∵MN是半圆的直径,
∴∠MDN=90°.
在Rt△MDN中,MN2=MD2+DN2,
∴两个小半圆的面积=大半圆的面积.
∴阴影部分的面积=△DMN的面积.
在Rt△AED中,DE=,
∴阴影部分的面积=△DMN的面积=MN AD=×6×6=18.
故答案为18.
20.解:阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积﹣以AB为直径的半圆的面积=扇形ABB′的面积,
则阴影部分的面积是:=6π,
故答案为:6π.
21.解:S阴影=4S半圆﹣S正方形
=4×π×22﹣4×4
=8π﹣16,
故答案为:8π﹣16
1.若一个扇形的圆心角为90°,半径是6,则它的弧长为 .
2.已知钟面上的分针长9厘米,那么分针针尖经过20分钟滑过的弧线长为 厘米.(结果保留π)
3.已知四边形ABCD是⊙O的内接四边形,⊙O半径是2,∠B=120°,则的长是 .
4.如图,⊙O的半径为1,四边形ABCD内接于⊙O,连接OB,OD,若∠BOD=∠BCD,则的长为 .
5.已知扇形的半径为10,弧长为10π,那么这个扇形的圆心角为 度.
6.一个扇形的半径为6,圆心角为120°,则该扇形的面积是 .
7.一个扇形的面积是12πcm2,圆心角是60°,则此扇形的半径是 cm.
8.已知圆心角为120°的扇形的面积为12πcm2,则扇形的弧长是 cm.
9.一个扇形的半径是6cm,弧长是5πcm,则此扇形的面积是 cm2.
10.若一个扇形的面积20,半径为8,则此扇形的弧长为 .
11.为庆祝祖国华诞,某单位排练的节目需用到如图所示的扇形布扇,布扇完全打开后,外侧两竹条AB,AC夹角为120°,AB的长为30cm,贴布部分BD的长为20cm,则贴布部分的面积约为 cm2.
12.如图,扇形AOB的圆心角是为90°,四边形OCDE是边长为1的正方形,点C,E分别在OA,OB,D在弧AB上,那么图中阴影部分的面积为 .(结果保留π)
13.如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为 .
14.如图,⊙O的半径是4cm,四边形ABCD是平行四边形,D是的中点,则阴影部分的面积是 cm2.
15.在Rt△ABC中,∠ACB=90°,AC=4,BC=2.分别以点B,A为圆心,以BC长为半径画弧,交AB于点D,E,交AC于点F,则图中的阴影部分的面积为 .(用含π的代数式表示)
16.如图,半圆O的直径AB=2,弦CD∥AB,∠COD=90°,则图中阴影部分的面积为 .
17.如图,在扇形AOB中,∠AOB=90°,OA=4,以OB为直径作半圆,圆心为点C,过点C作OA的平行线分别交两弧点D、E,则阴影部分的面积为 .
18.如图,将边长为4的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD的面积为 .
19.如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则黑色阴影部分的面积为 .
20.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是 .
21.如图,正方形ABCD的边长为4,分别以各边中点为圆心、边长为直径在正方形内部画圆,求阴影部分的面积 .(结果保留π)
参考答案
1.解:该扇形的弧长==3π.
故答案为:3π.
2.解:由题意可得,分针针尖经过20分钟滑过的弧线长为:=6π(厘米).
故答案为:6π.
3.解:如图,连接OC,OA.
∵∠B+∠D=180°,∠B=120°,
∴∠D=60°,
∴∠AOC=2∠D=120°,
∴的长==π,
故答案为:π.
4.解:由圆周角定理得,2∠BAD=∠BOD,
∵四边形ABCD是⊙O的内接四边形,
∴∠BCD=180°﹣∠BAD,
∴180°﹣∠BAD=2∠BAD,
解得,∠BAD=60°,
∴∠BOD=2∠BAD=120°,
∴的长==π,
故答案为:π.
5.解:由题意可得,
10π=,
解得n=180,
即这个扇形的圆心角为180°,
故答案为:180.
6.解:∵一个扇形的半径为6,圆心角为120°,
∴该扇形的面积是:=12π,
故答案为:12π.
7.解:设这个扇形的半径是rcm.
根据扇形面积公式,得=12π,
解得r=±6(负值舍去).
故答案为6.
8.解:令扇形的半径和弧长分别为R和l,则
∵S==12π,
∴R=6cm,
∴l==4πcm.
∴扇形的弧长为4πcm.
9.解:根据题意得,S扇形=lR==15π(cm2).
故答案为15π.
10.解:∵一个扇形的面积20,半径为8,
∴此扇形的弧长为:=5,
故答案为:5.
11.解:贴布部分的面积=S扇形BAC﹣S扇形DAE
=﹣
=(cm2).
故答案为.
12.解:∵四边形OCDE是边长为1的正方形,
∴OD=,
∴图中阴影部分的面积=S扇形AOB﹣S正方形OCDE
=﹣1
=π﹣1.
故答案为π﹣1.
13.解:设圆心为O,连接OA、OD.
∵AD∥BC,AC平分∠BCD,∠ADC=120°,
∴∠BCD=60°,
∵AC平分∠BCD,
∴∠ACD=30°,
∴∠AOD=2∠ACD=60°,∠OAC=∠ACO=30°.
∴∠BAC=90°,
∴∠ABC=60°,
又∵OA=OD=OB=OC,
则△AOD、△AOB、△COD都是等边三角形.
∴AB=AD=CD.
又∵四边形ABCD的周长为10cm,
∴OB=OC=AB=AD=DC=2(cm).
∴阴影部分的面积=S梯形﹣S△ABC=(2+4)×﹣×4×=3﹣2=.
故答案为.
14.解:连接OD,
∵D是弧AB的中点
∴∠DOA=∠DOB=90°,
∵OA=OD=4cm,
∴△OAD的面积为OA OD=8cm2,
扇形OAD的面积为:=4π,
∴阴影部分面积为:(4π﹣8)cm2.
故答案为:(4π﹣8).
15.解:∵∠ACB=90°,
∴∠A+∠B=90°,
∴S扇形EAF+S扇形DBC==π,
∴图中的阴影部分的面积=S△ABC﹣(S扇形EAF+S扇形DBC)
=×4×2﹣π
=4﹣π.
故答案为4﹣π.
16.解:∵弦CD∥AB,
∴S△ACD=S△OCD,
∴S阴影=S扇形COD= π =×π×=.
故答案为:.
17.解:连接OE,如图,
∵CE∥OA,
∴∠BCE=90°,
∵OE=4,OC=2,
∴CE=OC=2,
∴∠CEO=30°,∠BOE=60°,
∴S阴影部分=S扇形BOE﹣S△OCE﹣S扇形BCD=﹣×2×2﹣=π﹣2.
故答案为π﹣2
18.解:∵边长为4的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形,
∴的长度为8,
∴所得的扇形ABD的面积=×4×8=16.
故答案为:16.
19.解:根据图形可知阴影部分的面积=两个小的半圆的面积+△DMN的面积﹣大半圆的面积.
∵MN是半圆的直径,
∴∠MDN=90°.
在Rt△MDN中,MN2=MD2+DN2,
∴两个小半圆的面积=大半圆的面积.
∴阴影部分的面积=△DMN的面积.
在Rt△AED中,DE=,
∴阴影部分的面积=△DMN的面积=MN AD=×6×6=18.
故答案为18.
20.解:阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积﹣以AB为直径的半圆的面积=扇形ABB′的面积,
则阴影部分的面积是:=6π,
故答案为:6π.
21.解:S阴影=4S半圆﹣S正方形
=4×π×22﹣4×4
=8π﹣16,
故答案为:8π﹣16
