2021-2022学年鲁教版(五四制)六年级数学上册4.3一元一次方程的应用 同步练习题 (word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)六年级数学上册4.3一元一次方程的应用 同步练习题 (word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 172.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 00:00:00 | ||
图片预览




文档简介
2021-2022学年鲁教版六年级数学上册《4.3一元一次方程的应用》同步练习题(附答案)
1.《九章算术》是一部与现代数学的主流思想完全吻合的中国数学经典著作,全书分为九章,在第七章“均衡”中有一题:“今有凫起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”意思是:今有野鸭从南海起飞,7天到北海;大雁从北海起飞,9天到南海.现野鸭大雁同时起飞,问经过多少天相逢.利用方程思想解决这一问题时,设经过x天相遇,根据题意列出的方程是( )
A.(9﹣7)x=1 B.(9+7)x=1 C.(+)x=1 D.(﹣)x=1
2.《孙子算经》中有一道题,原文是:今有三人共车,二车空;二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车;若每2人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?设共有x人,可列方程( )
A.﹣9 B.+2= C.﹣2= D.+9
3.某校在庆祝祖国70周年“我和我的祖国”中学生读书系列活动中,将一些科技类图书分给了七年级一班的学生阅读,如果每人分4本,则剩余20本;如果每人分5本,则还缺30本.若设该校七年级一班有学生x人,则下列方程正确的是( )
A.4x﹣20=5x+30 B.4x+20=5x﹣30
C.4x﹣20=5x﹣30 D.4x+20=5x+30
4.我国古代名著《九章算术》中有一题:“今有凫起南海,七日至北海,雁起北海,九日至南海.今凫雁俱起,问何日相逢?”意思是:野鸭从南海起飞到北海需要7天;大雁从北海飞到南海需要9天.野鸭和大雁同时分别从南海和北海出发,多少天相遇?设野鸭与大雁从南海和北海同时起飞,经过x天相遇,可列方程为( )
A.9x﹣7x=1 B.9x+7x+1 C.x+x=1 D.x﹣x=1
5.如图,宽为50cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积为( )cm2.
A.400 B.500 C.300 D.750
6.用A、B两种规格的长方形纸板(如图1)无重合无缝隙的拼接可得如图2所示的周长为32cm的正方形,已知A种长方形的宽为1cm,则B种长方形的面积是( )
A.10cm2 B.12cm2 C.14cm2 D.16cm2
7.如图,长方形ABCD中有6个形状、大小相同的小长方形,且EF=3,CD=12,则图中阴影部分的面积为( )
A.108 B.72 C.60 D.48
8.如图(1),把一个长为m,宽为n的长方形(m>n)沿虚线剪开,拼接成图(2),成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长为( )
A. B.m﹣n C. D.
9.如图,是由7块正方形组成的长方形,已知中间小正方形的边长为1,则这个长方形的面积为( )
A.63 B.72 C.99 D.110
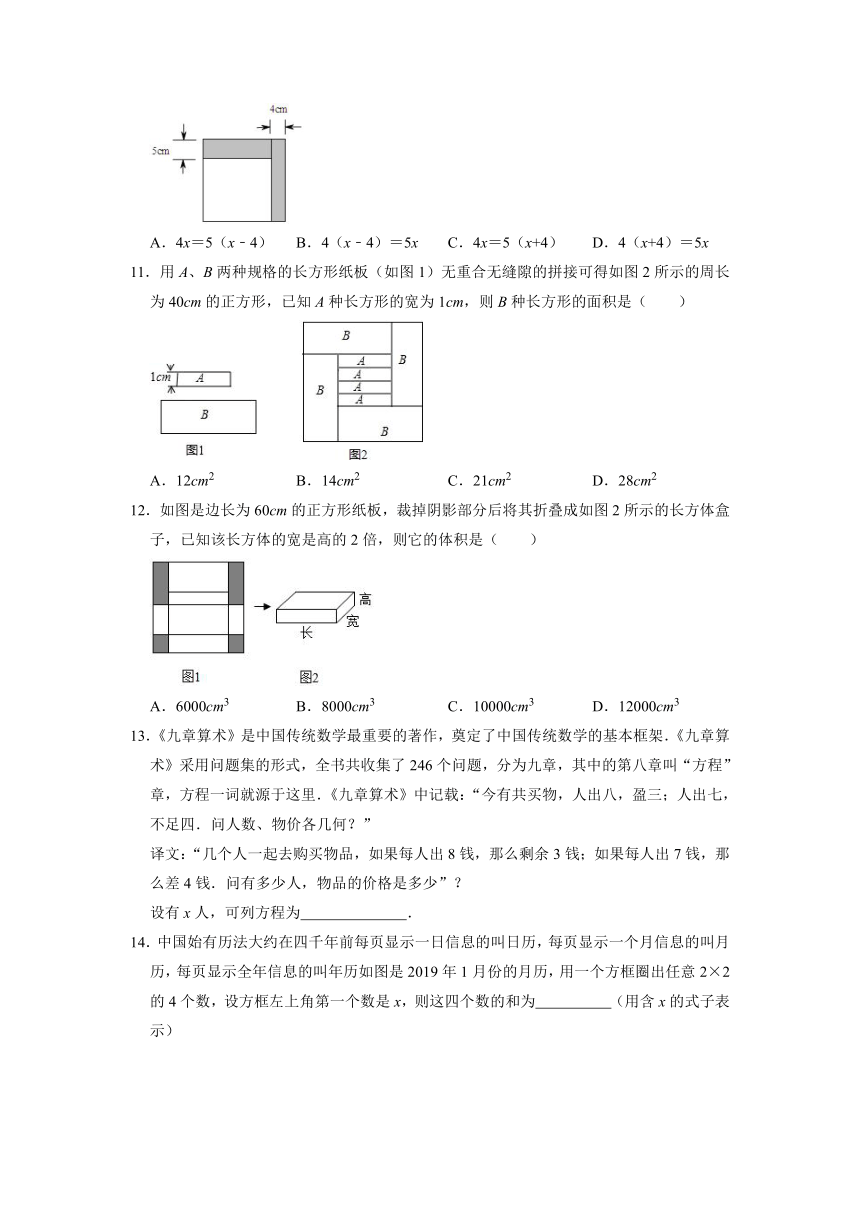
10.如图,轩轩将一个正方形纸片剪去一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条.如果两次剪下的长条面积正好相等,那么每一个长条的面积为多少?为解决这个问题,轩轩设正方形的边长为xcm,则依题意可得方程为( )
A.4x=5(x﹣4) B.4(x﹣4)=5x C.4x=5(x+4) D.4(x+4)=5x
11.用A、B两种规格的长方形纸板(如图1)无重合无缝隙的拼接可得如图2所示的周长为40cm的正方形,已知A种长方形的宽为1cm,则B种长方形的面积是( )
A.12cm2 B.14cm2 C.21cm2 D.28cm2
12.如图是边长为60cm的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是( )
A.6000cm3 B.8000cm3 C.10000cm3 D.12000cm3
13.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.《九章算术》采用问题集的形式,全书共收集了246个问题,分为九章,其中的第八章叫“方程”章,方程一词就源于这里.《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”
译文:“几个人一起去购买物品,如果每人出8钱,那么剩余3钱;如果每人出7钱,那么差4钱.问有多少人,物品的价格是多少”?
设有x人,可列方程为 .
14.中国始有历法大约在四千年前每页显示一日信息的叫日历,每页显示一个月信息的叫月历,每页显示全年信息的叫年历如图是2019年1月份的月历,用一个方框圈出任意2×2的4个数,设方框左上角第一个数是x,则这四个数的和为 (用含x的式子表示)
15.如图是由六个不同颜色的正方形组成的矩形,已知中间最小的一个正方形A的边长为1,那么矩形中正方形E的面积是 .
16.如图是2021年6月份的月历表,请仔细观察后,解答下列问题:
(1)月历表中,每行数字的大小规律是 ;
(2)月历表中,每列数字的大小规律是 ;
(3)若用正方形框框住几个数字,也会发现在一定方向上的排列也有规律,请再观察对角线“撇”方向的数字排列大小规律.“捺”方向的数字排列大小规律是 ;
(4)如果用正方形框把每9个数字框起来,发现中间的数字与它的四周的所有数字有一定关系,如果中间的数字设为x,那么四周数字的和一定是 ;
(5)如果发现用正方形框框住16个数字的和为224.试求出这16个数字中最大的数字.
17.《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四,问物价几何?译文为:现有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元,问这个物品的价格是多少元?
18.随着地铁2号线一期的开通,太原正式进入地铁时代.地铁2号线一期采用按里程分段计价的票制,全程最高票价为6元,学生可享受半价.周日,七年级某班师生共36人从始发站“西桥”乘地铁至终点站“尖草坪”,感受“地铁速度”.其中所有的学生享受了半价票,教师均买全价票,单程共付车票费用126元.参加本次活动的师生各多少人?
19.综合与实践
在数学综合与实践课上,老师以“出行方式的选择“为主题,请同学们发现和提出问题并分断和解决问题.
问题情境
随着互联网的普及和城市交通的多样化,人们出行的时间与方式有了更多的选择.某市有出租车.滴滴快车和神州专车三种网约车,收费标准见下图(该市规定网约车行驶的平均速度为40公里/时)
问题一
“奋进小组”提出的问题是:如果乘坐这三种网约车的里程数都是10公里.他们发现乘坐出租车最节省钱.费用为 元;
问题二
“质疑小组”提出了两个问题,请从A,B两个问题中任选一问作答,
A.从甲地到乙地,乘坐出租车比滴滴快车节省13.6元,求甲.乙两地间的里程数.
B.神州专车和滴滴快车对第一次下单的乘客有如下优惠活动:神州专车收费打八折,另外加5.3元的空车费;滴滴快车超过8公里收费立减6.5元.如果两位顾客都是第一次下单.分别乘坐神州专车、滴滴快车且收费相同,求这两位顾客乘车的里程数.
20.在“清洁乡村”活动中,某村长提出了两种购买垃圾桶方案.
方案一:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用250元;
方案二:买不分类垃圾桶,需要费用1000元,以后每月的垃圾处理费用500元.
设交费时间为x个月,方案一的购买费和垃圾处理费共为M元,方案二的购买费和垃圾处理费共为N元.
(1)分别用x表示M,N;
(2)若交费时间为12个月,哪种方案更合适,并说明理由.
(3)交费时间为多少个月时,两种方案费用相同?
21.用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.
现有38张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
22.整理一批图书,由一个人做要40小时完成.现计划由一部分人先做4小时,再增加2人和他们一起做8小时,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?
23.用8个形状和大小都相同的小长方形,恰好可以拼成如图1所示的大长方形;若用这8个小长方形拼成如图2所示的正方形,则中间留下一个空的小正方形(阴影部分).设小长方形的长和宽分别为a和b(a>b).
(1)由图1,可知a,b满足的等量关系是 ;
(2)若图2中小正方形的边长为2,求小长方形的面积;
(3)用含b的代数式表示图2中小正方形的面积.
24.如图是小红刚接手的新房的地面平面结构图(图中长度单位:米),其中每间房屋地面都是长方形,她准备在客厅和卧室地面全部铺设复合地板,厨房和卫生间地面全部铺设瓷砖,根据图中数据解决以下问题:
(1)该房屋厨房地面面积为 米2;该房屋地面总面积为 米2(用含x的代数式表示);
(2)铺设完全部地面,有两个施工计费方案供她选择:
方案一:每一平方米瓷砖的铺设费用为25元,每一平方米复合地板的铺设费用为30元;
方案二:铺完全部地面,一口价1500元.
试问当x为何值时两种方案一样省钱?若x=2,直接写出小红应该选择哪个方案更省钱呢?
参考答案
1.解:∵今有野鸭从南海起飞,7天到北海;大雁从北海起飞,9天到南海,
∴野鸭每天飞行的路程为两地间的距离的,大雁每天飞行的路程为两地间的距离的.
设经过x天相遇,
依题意得:(+)x=1.
故选:C.
2.解:依题意,得:+2=.
故选:B.
3.解:设该校七年级一班有学生x人,
依题意,得:4x+20=5x﹣30.
故选:B.
4.解:由题意可得,
,
故选:C.
5.解:设小长方形的长为xcm,则宽为(50﹣x)cm,根据题意可得:
2x=x+4(50﹣x),
解得:x=40,
故50﹣x=10(cm).
则一个小长方形的面积为:10×40=400(cm2).
故选:A.
6.解:设A长方形的长是xcm,则B长方形的宽是(4﹣x)cm,B长方形的长是(8﹣x)cm,依题意有
4[(4﹣x)+(8﹣x)]=32,
解得x=4,
(4﹣x)(8﹣x)
=(4﹣2)×(8﹣2)
=2×6
=12(cm2).
故B种长方形的面积是12cm2.
故选:B.
7.解:设每小长方形的宽为x,则每小长方形的长为x+3,根据题意得:
2(x+3)+x=12,
解得:x=2,
则每小长方形的长为2+3=5,
则AD=2+2+5=9,
阴影部分的面积为9×12﹣2×5×6=48;
故选:D.
8.解:设去掉的小正方形的边长为x,
则:(n+x)2=mn+x2,
解得:x=.
故选:A.
9.解:设正方形A的边长为x,则正方形B的边长为x+1,正方形C的边长为x+2,正方形D的边长为x+3,
根据图形得:x+2+x+3=3x+x+1,
解得:x=2,
则长方形的面积为(x+2+x+3)(x+1+x+2)=(2x+5)(2x+3)=9×7=63.
故选:A.
10.解:设正方形的边长为xcm,则第一个长条的长为xcm,宽为4cm,第二个长条的长为(x﹣4)cm,宽为5cm,
依题意得:4x=5(x﹣4).
故选:A.
11.解:设A长方形的长是xcm,则B长方形的宽是(5﹣x)cm,B长方形的长是(9﹣x)cm,依题意有
4[(5﹣x)+(9﹣x)]=40,
解得x=4,
(5﹣x)(9﹣x)
=(5﹣2)×(9﹣2)
=3×7
=21(cm2).
故B种长方形的面积是21cm2.
故选:C.
12.解:设长方体的高为xcm,则宽为2xcm,
根据题意得:
x+2x+x+2x=60,
解得x=10,
所以,长方体盒子的宽为20cm,长为60﹣20=40cm.
体积:40×10×20=8000(cm3).
故选:B.
13.解:由题意可得,
设有x人,可列方程为:8x﹣3=7x+4.
故答案为:8x﹣3=7x+4.
14.解:x+x+1+x+7+x+8=4x+16.
故答案是:4x+16.
15.解:设第二个小正方形D的边长是x,则其余正方形的边长为:x,x+1,x+2,x+3,
则根据题意得:x+x+(x+1)=x+2+x+3,
解得:x=4,
∴x+1=5,
∴矩形中正方形E的面积是5×5=25.
故答案为:25.
16.解:(1)观察每一行,相邻两个数之差都是1,
故答案为:相邻两个数之差为1.
(2)观察每一列,相邻两个数之差为7,
故答案为:相邻两个数之差为7.
(3)观察撇方向对角线的数,可知相邻两个数之差为6.观察捺方向对角线的数,可知相邻两个数之差为8.
故答案为:撇方向的规律:相邻两个数之差为6;捺方形的规律:相邻两个数之差为8.
(4)对四周数字的和:(x﹣8)+(x﹣7)+(x﹣6)+(x﹣1)+(x+1)+(x+6)+(x+7)+(x+8)=8x.
故答案为:8x.
(5)可以设16个数中左上角最小的数为x,16个数求和,列方程得:
x+(x+1)+(x+2)+(x+3)+(x+7)+(x+8)+(x+9)+(x+10)+(x+14)+(x+15)+(x+16)+(x+17)+(x+21)+(x+22)+(x+23)+(x+24)=224,
2x+192=224,
x=2.
2+24=26.
所以这16个数中最大的数为26.
17.解:设共同购买该物品的有x人,
依题意得:8x﹣3=7x+4,
解得:x=7,
∴8x﹣3=8×7﹣3=56﹣3=53.
答:这个物品的价格是53元.
18.解:设教师x人,则学生(36﹣x)人,依题意得:
6x+×6(36﹣x)=126,
解得x=6,
36﹣x=36﹣6=30.
答:教师6人,学生30人.
19.解:问题一:14+2.4×(10﹣3)=30.8(元)
问题二:A 解:设甲、乙两地间里程数为x公里
①若
解得:(舍)
②若x>3,
解得:x=12
答:甲、乙两地间里程数为12公里B.
B 解:设两位顾客的里程数为x公里
①若x≤8,
解得:x=5
②
解得:x=30
答:两位顾客的里程数为5或30公里.
20.解:(1)依题意,得M=250x+3000;N=500x+1000.
(2)当x=12时,M=250×12+3000=6000;
当x=12时,N=500×12+1000=7000.
∵6000<7000,
∴若交费时间为12个月,选择方案一更合适.
(3)依题意,得M=N,
即250x+3000=500x+1000,
解得x=8.
答:交费时间为8个月时,两种方案费用相同.
21.解:(1)∵裁剪时x张用A方法,
∴裁剪时(38﹣x)张用B方法.
∴侧面的个数为:6x+4(38﹣x)=(2x+152)个,
底面的个数为:5(38﹣x)=(190﹣5x)个;
(2)由题意,得(2x+152):(190﹣5x)=3:2,
解得:x=14,
∴盒子的个数为:=60.
答:裁剪出的侧面和底面恰好全部用完,能做60个盒子.
22.解:设应先安排x人工作,
根据题意得:+=1
化简可得:+=1,
即:x+2(x+2)=10
解可得:x=2
答:应先安排2人工作.
23.解:(1)∵图1是长方形,
∴3a=5b,
故答案为:3a=5b;
(2)∵3a=5b,
∴a=b,
由题意可得:2b﹣b=2,
∴b=6,
∴a=10,
∴小长方形的面积=10×6=60;
(3)∵小长方形的边长=2b﹣a=2b﹣b=,
∴小正方形的面积=()2=.
24.解:(1)该房屋厨房地面面积为3x米2;该房屋地面总面积为3x+(6﹣3)×2+3×(3+2)+2x×6=(15x+21)米2.
故答案为:3x;(15x+21);
(2)依题意有25[3x+(6﹣3)×2]+30[3×(3+2)+2x×6]=1500,
解得x=,
若x=2时,25[3x+(6﹣3)×2]+30[3×(3+2)+2x×6]=25×[3×2+(6﹣3)×2]+30×[3×(3+2)+2×2×6]=1470,
1470<1500.
故当x为时两种方案一样省钱;若x=2,小红应该选择方案一更省钱.
1.《九章算术》是一部与现代数学的主流思想完全吻合的中国数学经典著作,全书分为九章,在第七章“均衡”中有一题:“今有凫起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”意思是:今有野鸭从南海起飞,7天到北海;大雁从北海起飞,9天到南海.现野鸭大雁同时起飞,问经过多少天相逢.利用方程思想解决这一问题时,设经过x天相遇,根据题意列出的方程是( )
A.(9﹣7)x=1 B.(9+7)x=1 C.(+)x=1 D.(﹣)x=1
2.《孙子算经》中有一道题,原文是:今有三人共车,二车空;二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车;若每2人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?设共有x人,可列方程( )
A.﹣9 B.+2= C.﹣2= D.+9
3.某校在庆祝祖国70周年“我和我的祖国”中学生读书系列活动中,将一些科技类图书分给了七年级一班的学生阅读,如果每人分4本,则剩余20本;如果每人分5本,则还缺30本.若设该校七年级一班有学生x人,则下列方程正确的是( )
A.4x﹣20=5x+30 B.4x+20=5x﹣30
C.4x﹣20=5x﹣30 D.4x+20=5x+30
4.我国古代名著《九章算术》中有一题:“今有凫起南海,七日至北海,雁起北海,九日至南海.今凫雁俱起,问何日相逢?”意思是:野鸭从南海起飞到北海需要7天;大雁从北海飞到南海需要9天.野鸭和大雁同时分别从南海和北海出发,多少天相遇?设野鸭与大雁从南海和北海同时起飞,经过x天相遇,可列方程为( )
A.9x﹣7x=1 B.9x+7x+1 C.x+x=1 D.x﹣x=1
5.如图,宽为50cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积为( )cm2.
A.400 B.500 C.300 D.750
6.用A、B两种规格的长方形纸板(如图1)无重合无缝隙的拼接可得如图2所示的周长为32cm的正方形,已知A种长方形的宽为1cm,则B种长方形的面积是( )
A.10cm2 B.12cm2 C.14cm2 D.16cm2
7.如图,长方形ABCD中有6个形状、大小相同的小长方形,且EF=3,CD=12,则图中阴影部分的面积为( )
A.108 B.72 C.60 D.48
8.如图(1),把一个长为m,宽为n的长方形(m>n)沿虚线剪开,拼接成图(2),成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长为( )
A. B.m﹣n C. D.
9.如图,是由7块正方形组成的长方形,已知中间小正方形的边长为1,则这个长方形的面积为( )
A.63 B.72 C.99 D.110
10.如图,轩轩将一个正方形纸片剪去一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条.如果两次剪下的长条面积正好相等,那么每一个长条的面积为多少?为解决这个问题,轩轩设正方形的边长为xcm,则依题意可得方程为( )
A.4x=5(x﹣4) B.4(x﹣4)=5x C.4x=5(x+4) D.4(x+4)=5x
11.用A、B两种规格的长方形纸板(如图1)无重合无缝隙的拼接可得如图2所示的周长为40cm的正方形,已知A种长方形的宽为1cm,则B种长方形的面积是( )
A.12cm2 B.14cm2 C.21cm2 D.28cm2
12.如图是边长为60cm的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是( )
A.6000cm3 B.8000cm3 C.10000cm3 D.12000cm3
13.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.《九章算术》采用问题集的形式,全书共收集了246个问题,分为九章,其中的第八章叫“方程”章,方程一词就源于这里.《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”
译文:“几个人一起去购买物品,如果每人出8钱,那么剩余3钱;如果每人出7钱,那么差4钱.问有多少人,物品的价格是多少”?
设有x人,可列方程为 .
14.中国始有历法大约在四千年前每页显示一日信息的叫日历,每页显示一个月信息的叫月历,每页显示全年信息的叫年历如图是2019年1月份的月历,用一个方框圈出任意2×2的4个数,设方框左上角第一个数是x,则这四个数的和为 (用含x的式子表示)
15.如图是由六个不同颜色的正方形组成的矩形,已知中间最小的一个正方形A的边长为1,那么矩形中正方形E的面积是 .
16.如图是2021年6月份的月历表,请仔细观察后,解答下列问题:
(1)月历表中,每行数字的大小规律是 ;
(2)月历表中,每列数字的大小规律是 ;
(3)若用正方形框框住几个数字,也会发现在一定方向上的排列也有规律,请再观察对角线“撇”方向的数字排列大小规律.“捺”方向的数字排列大小规律是 ;
(4)如果用正方形框把每9个数字框起来,发现中间的数字与它的四周的所有数字有一定关系,如果中间的数字设为x,那么四周数字的和一定是 ;
(5)如果发现用正方形框框住16个数字的和为224.试求出这16个数字中最大的数字.
17.《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四,问物价几何?译文为:现有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元,问这个物品的价格是多少元?
18.随着地铁2号线一期的开通,太原正式进入地铁时代.地铁2号线一期采用按里程分段计价的票制,全程最高票价为6元,学生可享受半价.周日,七年级某班师生共36人从始发站“西桥”乘地铁至终点站“尖草坪”,感受“地铁速度”.其中所有的学生享受了半价票,教师均买全价票,单程共付车票费用126元.参加本次活动的师生各多少人?
19.综合与实践
在数学综合与实践课上,老师以“出行方式的选择“为主题,请同学们发现和提出问题并分断和解决问题.
问题情境
随着互联网的普及和城市交通的多样化,人们出行的时间与方式有了更多的选择.某市有出租车.滴滴快车和神州专车三种网约车,收费标准见下图(该市规定网约车行驶的平均速度为40公里/时)
问题一
“奋进小组”提出的问题是:如果乘坐这三种网约车的里程数都是10公里.他们发现乘坐出租车最节省钱.费用为 元;
问题二
“质疑小组”提出了两个问题,请从A,B两个问题中任选一问作答,
A.从甲地到乙地,乘坐出租车比滴滴快车节省13.6元,求甲.乙两地间的里程数.
B.神州专车和滴滴快车对第一次下单的乘客有如下优惠活动:神州专车收费打八折,另外加5.3元的空车费;滴滴快车超过8公里收费立减6.5元.如果两位顾客都是第一次下单.分别乘坐神州专车、滴滴快车且收费相同,求这两位顾客乘车的里程数.
20.在“清洁乡村”活动中,某村长提出了两种购买垃圾桶方案.
方案一:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用250元;
方案二:买不分类垃圾桶,需要费用1000元,以后每月的垃圾处理费用500元.
设交费时间为x个月,方案一的购买费和垃圾处理费共为M元,方案二的购买费和垃圾处理费共为N元.
(1)分别用x表示M,N;
(2)若交费时间为12个月,哪种方案更合适,并说明理由.
(3)交费时间为多少个月时,两种方案费用相同?
21.用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.
现有38张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
22.整理一批图书,由一个人做要40小时完成.现计划由一部分人先做4小时,再增加2人和他们一起做8小时,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?
23.用8个形状和大小都相同的小长方形,恰好可以拼成如图1所示的大长方形;若用这8个小长方形拼成如图2所示的正方形,则中间留下一个空的小正方形(阴影部分).设小长方形的长和宽分别为a和b(a>b).
(1)由图1,可知a,b满足的等量关系是 ;
(2)若图2中小正方形的边长为2,求小长方形的面积;
(3)用含b的代数式表示图2中小正方形的面积.
24.如图是小红刚接手的新房的地面平面结构图(图中长度单位:米),其中每间房屋地面都是长方形,她准备在客厅和卧室地面全部铺设复合地板,厨房和卫生间地面全部铺设瓷砖,根据图中数据解决以下问题:
(1)该房屋厨房地面面积为 米2;该房屋地面总面积为 米2(用含x的代数式表示);
(2)铺设完全部地面,有两个施工计费方案供她选择:
方案一:每一平方米瓷砖的铺设费用为25元,每一平方米复合地板的铺设费用为30元;
方案二:铺完全部地面,一口价1500元.
试问当x为何值时两种方案一样省钱?若x=2,直接写出小红应该选择哪个方案更省钱呢?
参考答案
1.解:∵今有野鸭从南海起飞,7天到北海;大雁从北海起飞,9天到南海,
∴野鸭每天飞行的路程为两地间的距离的,大雁每天飞行的路程为两地间的距离的.
设经过x天相遇,
依题意得:(+)x=1.
故选:C.
2.解:依题意,得:+2=.
故选:B.
3.解:设该校七年级一班有学生x人,
依题意,得:4x+20=5x﹣30.
故选:B.
4.解:由题意可得,
,
故选:C.
5.解:设小长方形的长为xcm,则宽为(50﹣x)cm,根据题意可得:
2x=x+4(50﹣x),
解得:x=40,
故50﹣x=10(cm).
则一个小长方形的面积为:10×40=400(cm2).
故选:A.
6.解:设A长方形的长是xcm,则B长方形的宽是(4﹣x)cm,B长方形的长是(8﹣x)cm,依题意有
4[(4﹣x)+(8﹣x)]=32,
解得x=4,
(4﹣x)(8﹣x)
=(4﹣2)×(8﹣2)
=2×6
=12(cm2).
故B种长方形的面积是12cm2.
故选:B.
7.解:设每小长方形的宽为x,则每小长方形的长为x+3,根据题意得:
2(x+3)+x=12,
解得:x=2,
则每小长方形的长为2+3=5,
则AD=2+2+5=9,
阴影部分的面积为9×12﹣2×5×6=48;
故选:D.
8.解:设去掉的小正方形的边长为x,
则:(n+x)2=mn+x2,
解得:x=.
故选:A.
9.解:设正方形A的边长为x,则正方形B的边长为x+1,正方形C的边长为x+2,正方形D的边长为x+3,
根据图形得:x+2+x+3=3x+x+1,
解得:x=2,
则长方形的面积为(x+2+x+3)(x+1+x+2)=(2x+5)(2x+3)=9×7=63.
故选:A.
10.解:设正方形的边长为xcm,则第一个长条的长为xcm,宽为4cm,第二个长条的长为(x﹣4)cm,宽为5cm,
依题意得:4x=5(x﹣4).
故选:A.
11.解:设A长方形的长是xcm,则B长方形的宽是(5﹣x)cm,B长方形的长是(9﹣x)cm,依题意有
4[(5﹣x)+(9﹣x)]=40,
解得x=4,
(5﹣x)(9﹣x)
=(5﹣2)×(9﹣2)
=3×7
=21(cm2).
故B种长方形的面积是21cm2.
故选:C.
12.解:设长方体的高为xcm,则宽为2xcm,
根据题意得:
x+2x+x+2x=60,
解得x=10,
所以,长方体盒子的宽为20cm,长为60﹣20=40cm.
体积:40×10×20=8000(cm3).
故选:B.
13.解:由题意可得,
设有x人,可列方程为:8x﹣3=7x+4.
故答案为:8x﹣3=7x+4.
14.解:x+x+1+x+7+x+8=4x+16.
故答案是:4x+16.
15.解:设第二个小正方形D的边长是x,则其余正方形的边长为:x,x+1,x+2,x+3,
则根据题意得:x+x+(x+1)=x+2+x+3,
解得:x=4,
∴x+1=5,
∴矩形中正方形E的面积是5×5=25.
故答案为:25.
16.解:(1)观察每一行,相邻两个数之差都是1,
故答案为:相邻两个数之差为1.
(2)观察每一列,相邻两个数之差为7,
故答案为:相邻两个数之差为7.
(3)观察撇方向对角线的数,可知相邻两个数之差为6.观察捺方向对角线的数,可知相邻两个数之差为8.
故答案为:撇方向的规律:相邻两个数之差为6;捺方形的规律:相邻两个数之差为8.
(4)对四周数字的和:(x﹣8)+(x﹣7)+(x﹣6)+(x﹣1)+(x+1)+(x+6)+(x+7)+(x+8)=8x.
故答案为:8x.
(5)可以设16个数中左上角最小的数为x,16个数求和,列方程得:
x+(x+1)+(x+2)+(x+3)+(x+7)+(x+8)+(x+9)+(x+10)+(x+14)+(x+15)+(x+16)+(x+17)+(x+21)+(x+22)+(x+23)+(x+24)=224,
2x+192=224,
x=2.
2+24=26.
所以这16个数中最大的数为26.
17.解:设共同购买该物品的有x人,
依题意得:8x﹣3=7x+4,
解得:x=7,
∴8x﹣3=8×7﹣3=56﹣3=53.
答:这个物品的价格是53元.
18.解:设教师x人,则学生(36﹣x)人,依题意得:
6x+×6(36﹣x)=126,
解得x=6,
36﹣x=36﹣6=30.
答:教师6人,学生30人.
19.解:问题一:14+2.4×(10﹣3)=30.8(元)
问题二:A 解:设甲、乙两地间里程数为x公里
①若
解得:(舍)
②若x>3,
解得:x=12
答:甲、乙两地间里程数为12公里B.
B 解:设两位顾客的里程数为x公里
①若x≤8,
解得:x=5
②
解得:x=30
答:两位顾客的里程数为5或30公里.
20.解:(1)依题意,得M=250x+3000;N=500x+1000.
(2)当x=12时,M=250×12+3000=6000;
当x=12时,N=500×12+1000=7000.
∵6000<7000,
∴若交费时间为12个月,选择方案一更合适.
(3)依题意,得M=N,
即250x+3000=500x+1000,
解得x=8.
答:交费时间为8个月时,两种方案费用相同.
21.解:(1)∵裁剪时x张用A方法,
∴裁剪时(38﹣x)张用B方法.
∴侧面的个数为:6x+4(38﹣x)=(2x+152)个,
底面的个数为:5(38﹣x)=(190﹣5x)个;
(2)由题意,得(2x+152):(190﹣5x)=3:2,
解得:x=14,
∴盒子的个数为:=60.
答:裁剪出的侧面和底面恰好全部用完,能做60个盒子.
22.解:设应先安排x人工作,
根据题意得:+=1
化简可得:+=1,
即:x+2(x+2)=10
解可得:x=2
答:应先安排2人工作.
23.解:(1)∵图1是长方形,
∴3a=5b,
故答案为:3a=5b;
(2)∵3a=5b,
∴a=b,
由题意可得:2b﹣b=2,
∴b=6,
∴a=10,
∴小长方形的面积=10×6=60;
(3)∵小长方形的边长=2b﹣a=2b﹣b=,
∴小正方形的面积=()2=.
24.解:(1)该房屋厨房地面面积为3x米2;该房屋地面总面积为3x+(6﹣3)×2+3×(3+2)+2x×6=(15x+21)米2.
故答案为:3x;(15x+21);
(2)依题意有25[3x+(6﹣3)×2]+30[3×(3+2)+2x×6]=1500,
解得x=,
若x=2时,25[3x+(6﹣3)×2]+30[3×(3+2)+2x×6]=25×[3×2+(6﹣3)×2]+30×[3×(3+2)+2×2×6]=1470,
1470<1500.
故当x为时两种方案一样省钱;若x=2,小红应该选择方案一更省钱.
