2021-2022学年鲁教版(五四制)六年级数学上册4.3一元一次方程的应用 同步练习题 (word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)六年级数学上册4.3一元一次方程的应用 同步练习题 (word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 179.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 17:44:36 | ||
图片预览




文档简介
2021-2022学年鲁教版六年级数学上册《4.3一元一次方程的应用》同步练习题(附答案)
1.公元前4世纪的印度巴克沙利手稿中记载着一题:甲、乙、丙、丁四人各持金,乙为甲的二倍,丙为乙的三倍,丁为丙的四倍,并知四人持金的总数为132卢比,则乙的持金数为( )
A.4卢比 B.8卢比 C.12卢比 D.16卢比
2.欣欣服装店某天用相同的价格a(a>0)卖出了两件服装,其中一件盈利20%,另一件亏损20%,那么该服装店卖出这两件服装的盈利情况是( )
A.盈利 B.亏损
C.不盈不亏 D.与售价a有关
3.A、B两地相距350千米,甲、乙两车分别从A、B两地同时出发,相向而行.已知甲车速度为120千米/时,乙车速度为80千米/时,经过t小时两车相距50千米,则t的值是( )
A.2 B.1.5 C.2或1.5 D.2或2.5
4.某城市按以下规定收取每月煤气费:用煤气如果不超过60立方米,按每立方米0.8元收费;如果超过60立方米,超过部分按每立方米1.2元收费.已知某用户4月份的煤气费平均每立方米0.88元,那么4月份该用户应交煤气费( )
A.60元 B.66元 C.75元 D.78元
5.某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个,2个甲种部件和3个乙种部件配成一套,问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套?设安排x人加工甲部件,则列方程 .
6.李勇同学假期打工收入了一笔钱,他立即存入银行,存期为一年,整存整取,若年利率为2.16%.一年后李勇同学共得到本息和510.8元,则李勇同学存入 元.
7.轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/小时,水速为2千米/时,则A港和B港相距 千米.
8.某种商品因换季准备打折出售,如果按照原定价的七五折出售,每件将赔10元,而按原定价的九折出售,每件将赚38元,则这种商品的原定价是 元.
9.某商店换季促销,将一件标价为240元的T恤8折售出,仍获利20%,则这件T恤的成本为 .
10.当x= 时,代数式与x﹣3的值互为相反数.
11.某网店举行“三周年店庆,回馈老顾客”促销活动,制定的促销方案如表所示,其中表格中的x指的是购物原价(单位:元):
购物原价 x≤100 100<x≤300 x>300
优惠措施 无优惠 按原价的九折优惠 300元部分按九折优惠,超过300元的部分按八折优惠
在促销活动期间,小李在该网店购物两次:
(1)小李第一次在该网店购物,实际付款92.7元,小李此次购物的原价为多少元?
(2)小李第二次在该网店购物,实际付款278元,小李此次购物的原价为多少元?
12.微信运动和腾讯公益推出了一个爱心公益活动:一天中走路若步数达到10000步及以上,则可通过微信运动和腾讯基金会向公益活动捐款,每步可捐0.0002元;若步数在10000步以下,则不能参与爱心公益捐款.
(1)某天小齐的步数为15000步,求他这天为爱心公益可捐款多少钱?
(2)已知甲、乙、丙三人某天通过步数共捐款8.4元,且甲的步数:乙的步数:丙的步数=1:2:3,求这天甲走了多少步?
13.将连续的奇数1,3,5,7,9,…排成如图所示:
(1)十字框中5个数之和是41的几倍?
(2)设十字框中间的数为a,用代数式表示这十字框中五个数的和.
(3)十字框中的五个数之和能等于2 000吗?若能,请写出这五个数,若不能,请说明理由.
14.探究:将自然数1至2024按图中方式排成一个长方形阵列,用一个正方形框出9个数,
(1)图中的9个数的和是多少?
(2)能否使一个长方形框出的9个数的和为2034?若不可能,请说明理由;若可能,求出9个数中最大的数.
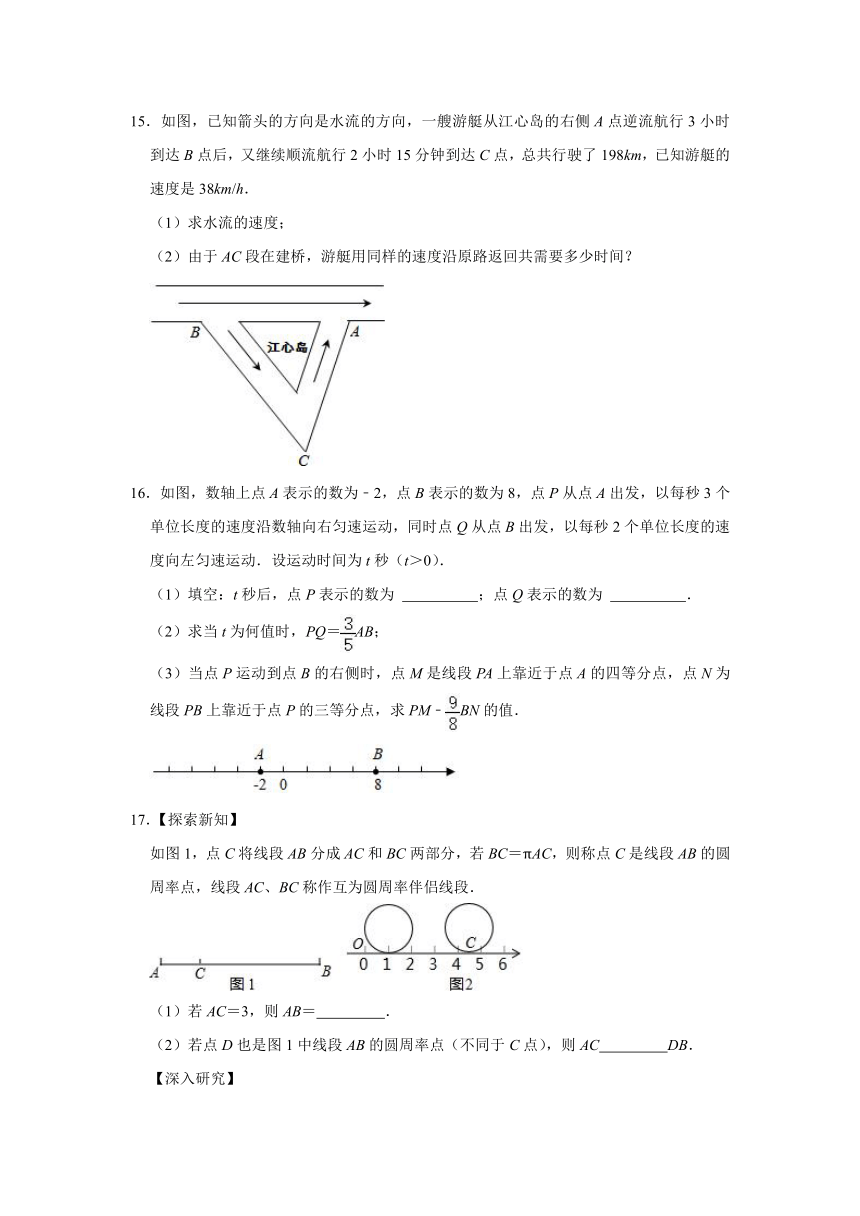
15.如图,已知箭头的方向是水流的方向,一艘游艇从江心岛的右侧A点逆流航行3小时到达B点后,又继续顺流航行2小时15分钟到达C点,总共行驶了198km,已知游艇的速度是38km/h.
(1)求水流的速度;
(2)由于AC段在建桥,游艇用同样的速度沿原路返回共需要多少时间?
16.如图,数轴上点A表示的数为﹣2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
(1)填空:t秒后,点P表示的数为 ;点Q表示的数为 .
(2)求当t为何值时,PQ=AB;
(3)当点P运动到点B的右侧时,点M是线段PA上靠近于点A的四等分点,点N为线段PB上靠近于点P的三等分点,求PM﹣BN的值.
17.【探索新知】
如图1,点C将线段AB分成AC和BC两部分,若BC=πAC,则称点C是线段AB的圆周率点,线段AC、BC称作互为圆周率伴侣线段.
(1)若AC=3,则AB= .
(2)若点D也是图1中线段AB的圆周率点(不同于C点),则AC DB.
【深入研究】
如图2,现有一个直径为1个单位长度的圆片,将圆片上的某点与数轴上表示1的点重合,并把圆片沿数轴向右无滑动地滚动1周,该点到达点C的位置.
(3)若点M、N均为线段OC的圆周率点,求线段MN的长度;
(4)在图2中,点P、Q分别从点O、C位置同时出发,分别以每秒2个单位长度、每秒1个单位长度的速度向右匀速运动,运动时间为t秒,点P追上点Q时,停止运动,当P、C、Q三点中某一点为其余两点所构成线段的圆周率点时,请直接写出t的值.
18.如图所示,A,B是数轴上的两个动点,两点的运动速度比为1:4.
(1)当A,B两点同时从原点出发,3秒后A,B两点相距15个单位传长度,求A,B两个点的速度,并在数轴上标出此时的位置;
(2)若A,B两点从(1)的最终位置同时按原速度沿负方向运动,当AB的中点为原点时,求运动的时间.
(3)若A,B两点从(1)的最终位置同时按原速度沿负方向运动,几秒时原点到点A和点B的距离的比是1:2?
(4)若A,B两点从(1)的最终位置同时按原速度沿负方向运动,第三个动点C同时从点B的位置出发向点A运动,当遇点A后立即返回向B运动,遇到B后又立即返回向A运动,如此往返,直到B追上A时,C立即停止运动,若点C的运动速度是每秒20个单位长度,那么点C从开始到停止运动,行驶的路程是多少单位长度?
19.A、B、C为数轴上三点,若点C到点A的距离是点C到点B的距离的2倍,则称点C是(A,B)的奇异点,例如图1中,点A表示的数为﹣1,点B表示的数为2,表示1的点C到点A的距离为2,到点B的距离为1,则点C是(A,B)的奇异点,但不是(B,A)的奇异点.
(1)在图1中,直接说出点D是(A,B)还是(B,C)的奇异点;
(2)如图2,若数轴上M、N两点表示的数分别为﹣2和4,(M,N)的奇异点K在M、N两点之间,请求出K点表示的数;
(3)如图3,A、B在数轴上表示的数分别为﹣20和40,现有一点P从点B出发,向左运动.
①若点P到达点A停止,则当点P表示的数为多少时,P、A、B中恰有一个点为其余两点的奇异点?
②若点P到达点A后继续向左运动,是否存在使得P、A、B中恰有一个点为其余两点的奇异点的情况?若存在,请直接写出此时PB的距离;若不存在,请说明理由.
20.一部分同学围在一起做“传数”游戏,我们把某同学传给后面的同学的数称为该同学的“传数”.游戏规则是:同学1心里先想好一个数,将这个数乘2再加1后传给同学2,同学2把同学1告诉他的数除以2再减后传给同学3,同学3把同学2传给他的数乘2再加1后传给同学4,同学4把同学3告诉他的数除以2再减后传给同学5,同学5把同学4传给他的数乘2再加1后传给同学6,…,按照上述规律,序号排在前面的同学继续依次传数给后面的同学,直到传数给同学1为止.
(1)若只有同学1,同学2,同学3做“传数”游戏.
①同学1心里想好的数是2,则同学3的“传数”是 ;
②这三个同学的“传数”之和为17,则同学1心里先想好的数是 .
(2)若有n个同学(n为大于1的偶数)做“传数”游戏,这n个同学的“传数”之和为20n,求同学1心里先想好的数.
参考答案
1.解:设乙的持金数为x卢比,
则甲的持金数为x卢比,丙的持金数为3x卢比,丁的持金数为12x卢比,
由题意得:x+x+3x+12x=132,
解得:x=8,
∴乙的持金数为8卢比,
故选:B.
2.解:设第一件衣服的进价为x元,
依题意得:x(1+20%)=a,
设第二件衣服的进价为y元,
依题意得:y(1﹣20%)=a,
∴x(1+20%)=y(1﹣20%),
整理得:3x=2y,
该服装店卖出这两件服装的盈利情况为:0.2x﹣0.2y=0.2x﹣0.3x=﹣0.1x,
即赔了0.1x元,
故选:B.
3.解:根据题意得120t+80t=350﹣50或120t+80t=350+50,
解得t=1.5或t=2.
答:t的值是2或1.5.
故选:C.
4.解:设4月份用了煤气x立方,
则60×0.8+(x﹣60)×1.2=0.88×x,
解得:x=75,
75×0.88=66元,
故选:B.
5.解:设安排x人加工甲部件,则安排(85﹣x)人加工乙部件,根据题意得
3×16x=2×10×(85﹣x),
故答案是:3×16x=2×10×(85﹣x).
6.解:设李勇同学存入x元,
根据题意,得x+2.16%x=510.8
解得x=500
即李勇同学存入500元.
故答案是:500.
7.解:设A港和B港相距x千米.
根据题意,得,
解之得x=504.
故填504.
8.解:设商品的原定价为x元,
由题意得75%x+10=90%x﹣38,
解得x=320,
答:商品的原定价为320元.
故答案为320.
9.解:设成本为x元,则获利为20%x元,售价为0.8×240元,
由题意得:x+20%x=0.8×240,
解得:x=160.
答:这件T恤的成本为160元.
故答案为160元.
10.解:∵代数式与x﹣3的值互为相反数,
∴+x﹣3=0,
解得:x=.
故答案为:.
11.解:(1)因为100×0.9=90<92.7<100,
所以有两种情况:
情况1:小李第一次购物没有优惠,则小李购物原价为92.7元,
情况2:小李第一次购物原价超过100元,则第一次购物原价为:92.7÷0.9=103(元),
所以小李第一次购物原价为92.7或103元;
(2)300×0.9=270<278,
所以此次购物原价超过300元,设小李购物的原价为x元,
(x﹣300)×0.8+300×0.9=278,
解得:x=310,
所以第二次购物原价为310元,
答:小李第一次购物原价为92.7或103元,小李第二次购物原价为310元.
12.解:(1)小齐某天的步数为15000步,则他当日可捐:0.0002×15000=3(元).
故他这天为爱心公益可捐款3元钱;
(2)设这天甲走了x步,则乙走了2x步,丙走了x步,
分两种情况:
①如果x<10000,
根据题意可得0.0002(2x+3x)=8.4,
解得x=8400,符合题意;
②如果x≥10000,
根据题意,可得0.0002(x+2x+3x)=8.4,
解得x=7000,不合题意舍去;
答:甲走了8400步.
13.解:(1)(25+39+41+43+57)÷41=205÷41=5,
答:十字框中5个数之和是41的5倍.
(2)∵十字框中间的数为a,
∴这十字框中五个数的和为[(a﹣16)+(a﹣2)+a+(a+2)+(a+16)]=5a.
(3)假设能,设中间的数为x,
根据题意,得:5x=2000,
解得:x=400.
∵400为偶数,
∴假设不成立,即十字框中的五个数之和不能等于2000.
14.解:(1)17×3+24×3+31×3=216;
(2)设长方形框的第二列中间数为a,则中间的一列的三个数的和是:3a,第一列的3个数的和是3(a﹣1),第3列的3个数的和是3(a+1),
3a+3(a﹣1)+3(a+1)=2034,
解得a=226,即可能,
则最大数是226+1+7=234.
15.解:(1)设水流速度为x km/h,则游艇的顺流速度为(x+38)km/h,游艇的逆流航行速度为(38﹣x)km/h.
据题意可得,.
解得x=2.
∴水流的速度为2km/h.
(2)由(1)可知,顺流航行速度为40km/h,逆流航行的速度为36km/h.
∴AB段的路程为3×36=108(km),BC段的路程为.
故原路返回时间为:.
答:游艇用同样的速度原路返回共需要5小时12分.
16.解:(1)t秒后,点P表示的数为﹣2+3t;点Q表示的数为8﹣2t.
故答案为:﹣2+3t;8﹣2t;
(2)根据题意得:
|(﹣2+3t)﹣(8﹣2t)|=×10,
|5t﹣10|=6,
解得:t=或,
∴当t=或时,PQ=AB;
(3)根据题意得
PM=,
BN=BP=(AP﹣AB)=×(3t﹣10)=2t﹣,
∴PM﹣BN=t﹣(2t﹣)=.
17.解:(1)∵AC=3,BC=πAC
∴BC=3π
∴AB=AC+BC=3π+3
故答案为:3π+3.
(2)∵BC=πAC
∴当BD=AC时,有AD=πBD
即点D是线段AB的圆周率点
故答案为:=.
(3)由题意可知,点C表示的数是π+1
若点M、N均为线段OC的圆周率点,不妨设M点离O点近,且OM=x,则
x+πx=π+1
解得:x=1
∴MN=π+1﹣1﹣1=π﹣1.
(4)由题意可知,点P、C、Q所表示的数分别为:2t、π+1、π+1+t
当P、C、Q三点中某一点为其余两点所构成线段的圆周率点时,有以下四种情况:
①点P在点C左侧,PC=πCQ
∴π+1﹣2t=πt
解得:t=;
②点P在点C左侧,πPC=CQ
∴π(π+1﹣2t)=t
解得:t=;
③点P在点C、点Q之间,且πPC=PQ
∴π(2t﹣π﹣1)=π+1+t﹣2t
解得:t=
④点P在点C、点Q之间,且PC=πPQ
∴2t﹣π﹣1=π(π+1+t﹣2t)
解得:t=.
∴符合题意的t的值为:、、、.
18.解:(1)设A点运动速度为x单位长度/秒,则B点运动速度为4x单位长度/秒.
由题意得:3x+3×4x=15,
解得:x=1
..A点的运动速度是1单位长度/秒,B点的速度是4单位长度/秒;
(2)设y秒后,原点恰好处在A、B的正中间.
由题意得:y+3=12﹣4y,
解得:y=,
答:经过秒后,原点恰处在A、B的正中间;
(3)设经过t秒后,原点到A和B的距离的比是1:2,
①当A、B两点在原点两侧时,
由题意得,
解得:t=1,
②当A、B两点在原点同一侧,都在x轴负半轴上时,
由题意得,
解得:t=9,
答:经过1秒或9秒时,原点到A、B的距离的比是1:2;
(4)设B追上A需要时间m秒,
则:4m﹣m=15,
解得:m=5,
20×5=100.
答:C点行驶的路程是100单位长度.
19.解:(1)在图1中,点D到点A的距离为1,到点B的距离为2,到C的距离是1,
∴点D是(B,C)的奇异点,不是(A,B)的奇异点;
(2)设奇异点表示的数为x,
则由题意,得x﹣(﹣2)=2(4﹣x).
解得x=2.
∴(M,N)的奇异点表示的数是2;
(3)①设点P表示的数为y.
当点P是(A,B)的奇异点时,
则有y+20=2(40﹣y),
解得y=20.
当点P是(B,A)的奇异点时,
则有40﹣y=2(y+20),
解得y=0.
当点A是(B,P)的奇异点时,
则有40+20=2(y+20),
解得y=10.
当点B是(A,P)的奇异点时,
则有40+20=2(40﹣y),解得y=10.
∴当点P表示的数是0或10或20时,
P、A、B中恰有一个点为其余两点的奇异点.
②当点P为(B,A)的奇异点时,PB=120;
当点A为(P,B)的奇异点时,PB=180;
当点A为(B,P)的奇异点时,PB=90;
当点B为(P,A)的奇异点时,PB=120.
20.解:(1)①由题意得:2×2+1=5,
5÷2﹣=2,
2×2+1=5,
故同学3的“传数”是5;
②设同学1想好的数是a,则(2a+1)+(2a+1)÷2﹣+[(2a+1)÷2﹣]×2+1=17,
解得:a=3,
故答案为:3.
(2)设同学1心里先想好的数为x,则依题意:
同学1的“传数”是2x+1,
同学2的“传数”是,
同学3的“传数”是2x+1,
同学4的“传数”是x,…,
同学n(n为大于1的偶数)的“传数”是x.
于是.
(3x+1)n=40n.
∵n为大于1的偶数,
∴n≠0.
∴3x+1=40.
解得 x=13.
因此同学1心里先想好的数是13.
1.公元前4世纪的印度巴克沙利手稿中记载着一题:甲、乙、丙、丁四人各持金,乙为甲的二倍,丙为乙的三倍,丁为丙的四倍,并知四人持金的总数为132卢比,则乙的持金数为( )
A.4卢比 B.8卢比 C.12卢比 D.16卢比
2.欣欣服装店某天用相同的价格a(a>0)卖出了两件服装,其中一件盈利20%,另一件亏损20%,那么该服装店卖出这两件服装的盈利情况是( )
A.盈利 B.亏损
C.不盈不亏 D.与售价a有关
3.A、B两地相距350千米,甲、乙两车分别从A、B两地同时出发,相向而行.已知甲车速度为120千米/时,乙车速度为80千米/时,经过t小时两车相距50千米,则t的值是( )
A.2 B.1.5 C.2或1.5 D.2或2.5
4.某城市按以下规定收取每月煤气费:用煤气如果不超过60立方米,按每立方米0.8元收费;如果超过60立方米,超过部分按每立方米1.2元收费.已知某用户4月份的煤气费平均每立方米0.88元,那么4月份该用户应交煤气费( )
A.60元 B.66元 C.75元 D.78元
5.某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个,2个甲种部件和3个乙种部件配成一套,问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套?设安排x人加工甲部件,则列方程 .
6.李勇同学假期打工收入了一笔钱,他立即存入银行,存期为一年,整存整取,若年利率为2.16%.一年后李勇同学共得到本息和510.8元,则李勇同学存入 元.
7.轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/小时,水速为2千米/时,则A港和B港相距 千米.
8.某种商品因换季准备打折出售,如果按照原定价的七五折出售,每件将赔10元,而按原定价的九折出售,每件将赚38元,则这种商品的原定价是 元.
9.某商店换季促销,将一件标价为240元的T恤8折售出,仍获利20%,则这件T恤的成本为 .
10.当x= 时,代数式与x﹣3的值互为相反数.
11.某网店举行“三周年店庆,回馈老顾客”促销活动,制定的促销方案如表所示,其中表格中的x指的是购物原价(单位:元):
购物原价 x≤100 100<x≤300 x>300
优惠措施 无优惠 按原价的九折优惠 300元部分按九折优惠,超过300元的部分按八折优惠
在促销活动期间,小李在该网店购物两次:
(1)小李第一次在该网店购物,实际付款92.7元,小李此次购物的原价为多少元?
(2)小李第二次在该网店购物,实际付款278元,小李此次购物的原价为多少元?
12.微信运动和腾讯公益推出了一个爱心公益活动:一天中走路若步数达到10000步及以上,则可通过微信运动和腾讯基金会向公益活动捐款,每步可捐0.0002元;若步数在10000步以下,则不能参与爱心公益捐款.
(1)某天小齐的步数为15000步,求他这天为爱心公益可捐款多少钱?
(2)已知甲、乙、丙三人某天通过步数共捐款8.4元,且甲的步数:乙的步数:丙的步数=1:2:3,求这天甲走了多少步?
13.将连续的奇数1,3,5,7,9,…排成如图所示:
(1)十字框中5个数之和是41的几倍?
(2)设十字框中间的数为a,用代数式表示这十字框中五个数的和.
(3)十字框中的五个数之和能等于2 000吗?若能,请写出这五个数,若不能,请说明理由.
14.探究:将自然数1至2024按图中方式排成一个长方形阵列,用一个正方形框出9个数,
(1)图中的9个数的和是多少?
(2)能否使一个长方形框出的9个数的和为2034?若不可能,请说明理由;若可能,求出9个数中最大的数.
15.如图,已知箭头的方向是水流的方向,一艘游艇从江心岛的右侧A点逆流航行3小时到达B点后,又继续顺流航行2小时15分钟到达C点,总共行驶了198km,已知游艇的速度是38km/h.
(1)求水流的速度;
(2)由于AC段在建桥,游艇用同样的速度沿原路返回共需要多少时间?
16.如图,数轴上点A表示的数为﹣2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
(1)填空:t秒后,点P表示的数为 ;点Q表示的数为 .
(2)求当t为何值时,PQ=AB;
(3)当点P运动到点B的右侧时,点M是线段PA上靠近于点A的四等分点,点N为线段PB上靠近于点P的三等分点,求PM﹣BN的值.
17.【探索新知】
如图1,点C将线段AB分成AC和BC两部分,若BC=πAC,则称点C是线段AB的圆周率点,线段AC、BC称作互为圆周率伴侣线段.
(1)若AC=3,则AB= .
(2)若点D也是图1中线段AB的圆周率点(不同于C点),则AC DB.
【深入研究】
如图2,现有一个直径为1个单位长度的圆片,将圆片上的某点与数轴上表示1的点重合,并把圆片沿数轴向右无滑动地滚动1周,该点到达点C的位置.
(3)若点M、N均为线段OC的圆周率点,求线段MN的长度;
(4)在图2中,点P、Q分别从点O、C位置同时出发,分别以每秒2个单位长度、每秒1个单位长度的速度向右匀速运动,运动时间为t秒,点P追上点Q时,停止运动,当P、C、Q三点中某一点为其余两点所构成线段的圆周率点时,请直接写出t的值.
18.如图所示,A,B是数轴上的两个动点,两点的运动速度比为1:4.
(1)当A,B两点同时从原点出发,3秒后A,B两点相距15个单位传长度,求A,B两个点的速度,并在数轴上标出此时的位置;
(2)若A,B两点从(1)的最终位置同时按原速度沿负方向运动,当AB的中点为原点时,求运动的时间.
(3)若A,B两点从(1)的最终位置同时按原速度沿负方向运动,几秒时原点到点A和点B的距离的比是1:2?
(4)若A,B两点从(1)的最终位置同时按原速度沿负方向运动,第三个动点C同时从点B的位置出发向点A运动,当遇点A后立即返回向B运动,遇到B后又立即返回向A运动,如此往返,直到B追上A时,C立即停止运动,若点C的运动速度是每秒20个单位长度,那么点C从开始到停止运动,行驶的路程是多少单位长度?
19.A、B、C为数轴上三点,若点C到点A的距离是点C到点B的距离的2倍,则称点C是(A,B)的奇异点,例如图1中,点A表示的数为﹣1,点B表示的数为2,表示1的点C到点A的距离为2,到点B的距离为1,则点C是(A,B)的奇异点,但不是(B,A)的奇异点.
(1)在图1中,直接说出点D是(A,B)还是(B,C)的奇异点;
(2)如图2,若数轴上M、N两点表示的数分别为﹣2和4,(M,N)的奇异点K在M、N两点之间,请求出K点表示的数;
(3)如图3,A、B在数轴上表示的数分别为﹣20和40,现有一点P从点B出发,向左运动.
①若点P到达点A停止,则当点P表示的数为多少时,P、A、B中恰有一个点为其余两点的奇异点?
②若点P到达点A后继续向左运动,是否存在使得P、A、B中恰有一个点为其余两点的奇异点的情况?若存在,请直接写出此时PB的距离;若不存在,请说明理由.
20.一部分同学围在一起做“传数”游戏,我们把某同学传给后面的同学的数称为该同学的“传数”.游戏规则是:同学1心里先想好一个数,将这个数乘2再加1后传给同学2,同学2把同学1告诉他的数除以2再减后传给同学3,同学3把同学2传给他的数乘2再加1后传给同学4,同学4把同学3告诉他的数除以2再减后传给同学5,同学5把同学4传给他的数乘2再加1后传给同学6,…,按照上述规律,序号排在前面的同学继续依次传数给后面的同学,直到传数给同学1为止.
(1)若只有同学1,同学2,同学3做“传数”游戏.
①同学1心里想好的数是2,则同学3的“传数”是 ;
②这三个同学的“传数”之和为17,则同学1心里先想好的数是 .
(2)若有n个同学(n为大于1的偶数)做“传数”游戏,这n个同学的“传数”之和为20n,求同学1心里先想好的数.
参考答案
1.解:设乙的持金数为x卢比,
则甲的持金数为x卢比,丙的持金数为3x卢比,丁的持金数为12x卢比,
由题意得:x+x+3x+12x=132,
解得:x=8,
∴乙的持金数为8卢比,
故选:B.
2.解:设第一件衣服的进价为x元,
依题意得:x(1+20%)=a,
设第二件衣服的进价为y元,
依题意得:y(1﹣20%)=a,
∴x(1+20%)=y(1﹣20%),
整理得:3x=2y,
该服装店卖出这两件服装的盈利情况为:0.2x﹣0.2y=0.2x﹣0.3x=﹣0.1x,
即赔了0.1x元,
故选:B.
3.解:根据题意得120t+80t=350﹣50或120t+80t=350+50,
解得t=1.5或t=2.
答:t的值是2或1.5.
故选:C.
4.解:设4月份用了煤气x立方,
则60×0.8+(x﹣60)×1.2=0.88×x,
解得:x=75,
75×0.88=66元,
故选:B.
5.解:设安排x人加工甲部件,则安排(85﹣x)人加工乙部件,根据题意得
3×16x=2×10×(85﹣x),
故答案是:3×16x=2×10×(85﹣x).
6.解:设李勇同学存入x元,
根据题意,得x+2.16%x=510.8
解得x=500
即李勇同学存入500元.
故答案是:500.
7.解:设A港和B港相距x千米.
根据题意,得,
解之得x=504.
故填504.
8.解:设商品的原定价为x元,
由题意得75%x+10=90%x﹣38,
解得x=320,
答:商品的原定价为320元.
故答案为320.
9.解:设成本为x元,则获利为20%x元,售价为0.8×240元,
由题意得:x+20%x=0.8×240,
解得:x=160.
答:这件T恤的成本为160元.
故答案为160元.
10.解:∵代数式与x﹣3的值互为相反数,
∴+x﹣3=0,
解得:x=.
故答案为:.
11.解:(1)因为100×0.9=90<92.7<100,
所以有两种情况:
情况1:小李第一次购物没有优惠,则小李购物原价为92.7元,
情况2:小李第一次购物原价超过100元,则第一次购物原价为:92.7÷0.9=103(元),
所以小李第一次购物原价为92.7或103元;
(2)300×0.9=270<278,
所以此次购物原价超过300元,设小李购物的原价为x元,
(x﹣300)×0.8+300×0.9=278,
解得:x=310,
所以第二次购物原价为310元,
答:小李第一次购物原价为92.7或103元,小李第二次购物原价为310元.
12.解:(1)小齐某天的步数为15000步,则他当日可捐:0.0002×15000=3(元).
故他这天为爱心公益可捐款3元钱;
(2)设这天甲走了x步,则乙走了2x步,丙走了x步,
分两种情况:
①如果x<10000,
根据题意可得0.0002(2x+3x)=8.4,
解得x=8400,符合题意;
②如果x≥10000,
根据题意,可得0.0002(x+2x+3x)=8.4,
解得x=7000,不合题意舍去;
答:甲走了8400步.
13.解:(1)(25+39+41+43+57)÷41=205÷41=5,
答:十字框中5个数之和是41的5倍.
(2)∵十字框中间的数为a,
∴这十字框中五个数的和为[(a﹣16)+(a﹣2)+a+(a+2)+(a+16)]=5a.
(3)假设能,设中间的数为x,
根据题意,得:5x=2000,
解得:x=400.
∵400为偶数,
∴假设不成立,即十字框中的五个数之和不能等于2000.
14.解:(1)17×3+24×3+31×3=216;
(2)设长方形框的第二列中间数为a,则中间的一列的三个数的和是:3a,第一列的3个数的和是3(a﹣1),第3列的3个数的和是3(a+1),
3a+3(a﹣1)+3(a+1)=2034,
解得a=226,即可能,
则最大数是226+1+7=234.
15.解:(1)设水流速度为x km/h,则游艇的顺流速度为(x+38)km/h,游艇的逆流航行速度为(38﹣x)km/h.
据题意可得,.
解得x=2.
∴水流的速度为2km/h.
(2)由(1)可知,顺流航行速度为40km/h,逆流航行的速度为36km/h.
∴AB段的路程为3×36=108(km),BC段的路程为.
故原路返回时间为:.
答:游艇用同样的速度原路返回共需要5小时12分.
16.解:(1)t秒后,点P表示的数为﹣2+3t;点Q表示的数为8﹣2t.
故答案为:﹣2+3t;8﹣2t;
(2)根据题意得:
|(﹣2+3t)﹣(8﹣2t)|=×10,
|5t﹣10|=6,
解得:t=或,
∴当t=或时,PQ=AB;
(3)根据题意得
PM=,
BN=BP=(AP﹣AB)=×(3t﹣10)=2t﹣,
∴PM﹣BN=t﹣(2t﹣)=.
17.解:(1)∵AC=3,BC=πAC
∴BC=3π
∴AB=AC+BC=3π+3
故答案为:3π+3.
(2)∵BC=πAC
∴当BD=AC时,有AD=πBD
即点D是线段AB的圆周率点
故答案为:=.
(3)由题意可知,点C表示的数是π+1
若点M、N均为线段OC的圆周率点,不妨设M点离O点近,且OM=x,则
x+πx=π+1
解得:x=1
∴MN=π+1﹣1﹣1=π﹣1.
(4)由题意可知,点P、C、Q所表示的数分别为:2t、π+1、π+1+t
当P、C、Q三点中某一点为其余两点所构成线段的圆周率点时,有以下四种情况:
①点P在点C左侧,PC=πCQ
∴π+1﹣2t=πt
解得:t=;
②点P在点C左侧,πPC=CQ
∴π(π+1﹣2t)=t
解得:t=;
③点P在点C、点Q之间,且πPC=PQ
∴π(2t﹣π﹣1)=π+1+t﹣2t
解得:t=
④点P在点C、点Q之间,且PC=πPQ
∴2t﹣π﹣1=π(π+1+t﹣2t)
解得:t=.
∴符合题意的t的值为:、、、.
18.解:(1)设A点运动速度为x单位长度/秒,则B点运动速度为4x单位长度/秒.
由题意得:3x+3×4x=15,
解得:x=1
..A点的运动速度是1单位长度/秒,B点的速度是4单位长度/秒;
(2)设y秒后,原点恰好处在A、B的正中间.
由题意得:y+3=12﹣4y,
解得:y=,
答:经过秒后,原点恰处在A、B的正中间;
(3)设经过t秒后,原点到A和B的距离的比是1:2,
①当A、B两点在原点两侧时,
由题意得,
解得:t=1,
②当A、B两点在原点同一侧,都在x轴负半轴上时,
由题意得,
解得:t=9,
答:经过1秒或9秒时,原点到A、B的距离的比是1:2;
(4)设B追上A需要时间m秒,
则:4m﹣m=15,
解得:m=5,
20×5=100.
答:C点行驶的路程是100单位长度.
19.解:(1)在图1中,点D到点A的距离为1,到点B的距离为2,到C的距离是1,
∴点D是(B,C)的奇异点,不是(A,B)的奇异点;
(2)设奇异点表示的数为x,
则由题意,得x﹣(﹣2)=2(4﹣x).
解得x=2.
∴(M,N)的奇异点表示的数是2;
(3)①设点P表示的数为y.
当点P是(A,B)的奇异点时,
则有y+20=2(40﹣y),
解得y=20.
当点P是(B,A)的奇异点时,
则有40﹣y=2(y+20),
解得y=0.
当点A是(B,P)的奇异点时,
则有40+20=2(y+20),
解得y=10.
当点B是(A,P)的奇异点时,
则有40+20=2(40﹣y),解得y=10.
∴当点P表示的数是0或10或20时,
P、A、B中恰有一个点为其余两点的奇异点.
②当点P为(B,A)的奇异点时,PB=120;
当点A为(P,B)的奇异点时,PB=180;
当点A为(B,P)的奇异点时,PB=90;
当点B为(P,A)的奇异点时,PB=120.
20.解:(1)①由题意得:2×2+1=5,
5÷2﹣=2,
2×2+1=5,
故同学3的“传数”是5;
②设同学1想好的数是a,则(2a+1)+(2a+1)÷2﹣+[(2a+1)÷2﹣]×2+1=17,
解得:a=3,
故答案为:3.
(2)设同学1心里先想好的数为x,则依题意:
同学1的“传数”是2x+1,
同学2的“传数”是,
同学3的“传数”是2x+1,
同学4的“传数”是x,…,
同学n(n为大于1的偶数)的“传数”是x.
于是.
(3x+1)n=40n.
∵n为大于1的偶数,
∴n≠0.
∴3x+1=40.
解得 x=13.
因此同学1心里先想好的数是13.
