2021-2022学年鲁教版(五四制)七年级数学上册6.4确定一次函数的表达式 同步练习题 (word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)七年级数学上册6.4确定一次函数的表达式 同步练习题 (word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 123.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 00:00:00 | ||
图片预览





文档简介
2021-2022学年鲁教版七年级数学上册《6.4确定一次函数的表达式》同步练习题(附答案)
1.小明根据某个一次函数关系式填写了的表格:则空格中的数为( )
x ﹣1 0 2
y ﹣3 6
A.16 B.8 C.12 D.24
2.函数y=2x+b的图象与两坐标轴围成的三角形的面积为4,则函数的表达式为( )
A.y=2x+4 B.y=2x﹣4
C.y=2x+4或 y=2x﹣4 D.y=﹣2x﹣4
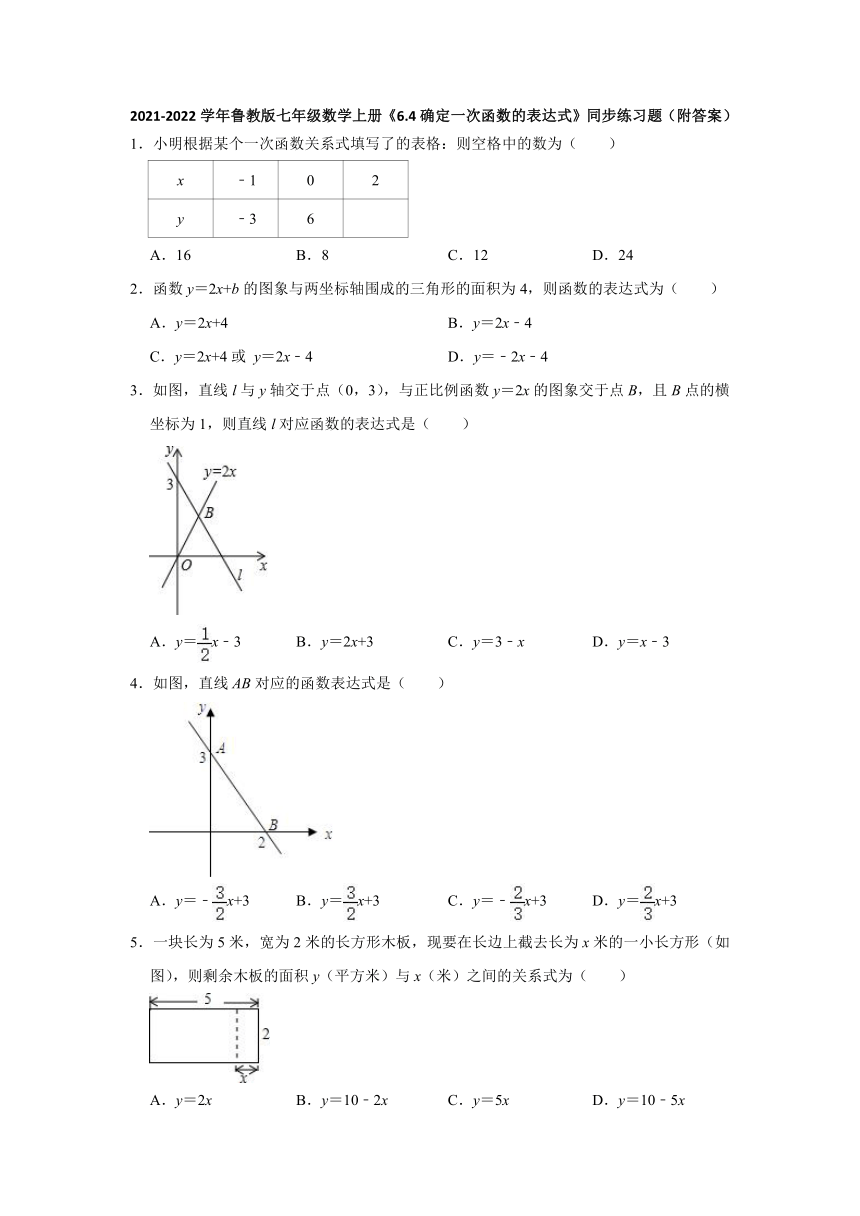
3.如图,直线l与y轴交于点(0,3),与正比例函数y=2x的图象交于点B,且B点的横坐标为1,则直线l对应函数的表达式是( )
A.y=x﹣3 B.y=2x+3 C.y=3﹣x D.y=x﹣3
4.如图,直线AB对应的函数表达式是( )
A.y=﹣x+3 B.y=x+3 C.y=﹣x+3 D.y=x+3
5.一块长为5米,宽为2米的长方形木板,现要在长边上截去长为x米的一小长方形(如图),则剩余木板的面积y(平方米)与x(米)之间的关系式为( )
A.y=2x B.y=10﹣2x C.y=5x D.y=10﹣5x
6.1千克某种水果5元,则所需钱数y(元)和水果重x(千克)之间的关系是( )
A.y=5x B.x=5y C. D.y=x+5
7.某水池现有水100m3,每小时进水20m3,排水15m3,t小时后水池中的水为Qm3,它的解析式为( )
A.Q=100+20t B.Q=100﹣15t C.Q=100+5t D.Q=100﹣5t
8.如果每盒圆珠笔有12支,售价18元,用y(元)表示圆珠笔的售价,x表示圆珠笔的支数,那么y与x之间的关系应该是( )
A.y=12x B.y=18x C.y=x D.y=x
9.如图所示,直线l的解析式是( )
A.y=x+2 B.y=﹣2x+2 C.y=x﹣2 D.y=﹣x﹣2
10.若直线y=kx+b经过点A(2,0),且与坐标轴围成的三角形的面积为6,则这条直线的表达式为 .
11.2021年1月1日,汽油价格为每升6.05元,张老师用一张面额为1000元的加油卡加油付费,则张老师卡上余额y(元)和加油量x(升)之间的函数关系式为 .
12.已知y是x的正比例函数,当x=1时y=﹣5,则当y=20时,x= .
13.若一次函数的图象经过点(0,﹣2),且与两坐标轴所围成的三角形面积为2,则这个函数的表达式为 .
14.若点P(﹣2,3)在直线y=﹣3x+b上,则b的值为 .
15.地面温度为15℃,在一定高度内如果高度每升高1千米,气温下降6℃.则气温t℃与高度h(千米)之间的关系式为 .
16.等腰三角形的周长为12厘米,底边长为y厘米,腰长为x厘米.则y与x的之间的关系式是y= (3<x<6).
17.某商店出售商品时,在进价的基础上又加了一定的利润,其数量x与售价y的关系如下表所示,那么售价y与数量x之间的关系式是 .
数量x(千克) 1 2 3 4 …
售价y(元) 8+0.4 16+0.8 24+1.2 32+1.6 …
18.商店出售一种瓜子数量x与售价c之间的关系如下表:
数量x(克) 售价c(元)
100 0.90+0.05
200 1.80+0.05
300 2.70+0.05
400 3.60+0.05
500 4.50+0 05
… …
(表内售价栏中的0.05是塑料袋的价钱)
则用含x的代数式表示c是 .
19.我国是一个严重缺水的国家,大家应倍加珍惜水资源,节约用水.据测试,拧不紧的水龙头每秒钟会滴下2滴水,每滴水约0.05毫升.小明同学在洗手后,没有把水龙头拧紧,当小明离开x小时后水龙头滴了y毫升水.试写出y关于x的函数关系式 .
20.在平面直角坐标系中,一次函数y=kx+b的图象(k≠0)与直线y=x﹣2相交于y轴上一点A,且图象经过点B(2,3)点O是坐标原点,求一次函数的解析式和△AOB的面积.
21.已知一次函数的图象过点(3,5)与点(﹣4,﹣9),求这个一次函数的解析式.
22.已知y﹣2与x+1成正比例函数,当x=1时,y=5.
(1)求y关于x的函数关系式;
(2)当x=﹣3时,求y的值.
23.如图,直线y=x+b与x轴交于点A,与y轴交于点B,且OB=2.
(1)求一次函数的关系式;
(2)若直线l过点B且与x轴交于点C,S△OBC=,求直线l的函数关系式.
24.已知一次函数y=kx+b的图象与x轴交于点A(﹣6,0),与y轴交于点B.若△AOB的面积为12,求一次函数的表达式.
参考答案
1.解:设一次函数的解析式为y=kx+b(k≠0),
∵x=﹣1时y=﹣3;x=0时,y=6,
∴,解得,
∴一次函数的解析式为y=9x+6,
∴当x=2时,y=18+6=24.
故选:D.
2.解:∵令x=0,则y=b,令y=0,则x=﹣,
∴函数y=2x+b的图象与两坐标轴的交点分别为(0,b),(﹣,0),
∴|b| |﹣|=4,解得b=±4,
∴函数的表达式为y=2x+4或y=2x﹣4.
故选:C.
3.解:设直线l对应函数的表达式为y=kx+b,
把x=1代入y=2x得y=2,则B点坐标为(1,2),
把B(1,2),(0,3)代入y=kx+b得,
解得,
所以直线l对应函数的表达式为y=﹣x+3.
故选:C.
4.解:设直线AB对应的函数表达式是y=kx+b,
把A(0,3),B(2,0)代入,
得,
解得,
故直线AB对应的函数表达式是y=﹣x+3.
故选:A.
5.解:由题意,有
y=2(5﹣x),
即y=10﹣2x.
故选:B.
6.解:设y=kx,然后根据题意列出关系式.
5=k 1,
∴k=5.
∴y=5x.
故选:A.
7.解:由题意得:Q=100+20t﹣15t=100+5t.
故选:C.
8.解:依题意有单价为18÷12=元,
则有y=x.
故选:D.
9.解:直线经过点(﹣2,0)和点(0,2),
因而可以设直线的解析式是y=k+b,
把点的坐标代入得到,
解得,
因而直线l的解析式是y=x+2.
故选:A.
10.解:把(2,0)代入得2k+b=0,解得b=﹣2k,
所以y=kx﹣2k,
把x=0代入得y=kx﹣2k得y=﹣2k,
所以直线与y轴的交点坐标为(0,﹣2k),
所以×2×|﹣2k|=6,解得k=3或﹣3,
所以所求的直线解析式为y=3x﹣6或y=﹣3x+6.
故答案为y=3x﹣6或y=﹣3x+6.
11.解:由题意得:
y与x的函数解析式为:y=1000﹣6.05x.
故答案为:y=1000﹣6.05x
12.解:设正比例函数的解析式为y=kx,
将x=1,y=﹣5代入,得﹣5=k,
所以y=﹣5x,
当y=20时,20=﹣5x,
解得x=﹣4.
故答案为﹣4.
13.解:由题意可设:y=kx﹣2,
与x轴交点为(,0),与y轴交点为(0,﹣2),
∴|| |﹣2|=2,
解得:k=1或﹣1,
∴函数解析式为y=x﹣2,或y=﹣x﹣2.
故答案是:y=x﹣2,或y=﹣x﹣2.
14.解:∵点P(﹣2,3)在直线y=﹣3x+b上,
∴点P(﹣2,3)满足直线y=﹣3x+b,
∴3=(﹣3)×(﹣2)+b
解得,b=﹣3;
故答案是:﹣3.
15.解:∵当高度为h时,降低6h,
∴气温t℃与高度h(千米)之间的关系式为 t=15﹣6h.
故答案为t=15﹣6h.
16.解:∵2x+y=12
∴y=﹣2x+12
∵x>6÷2=3,y<2x
∴3<x<6
即腰长y与底边x的函数关系是:y=﹣2x+12(3<x<6).
17.解:设y=kx,然后根据题意列出关系式.
8+0.4=k,
k=8.4.
∴y=8.4x.
故答案为:y=8.4x.
18.解:∵100克的瓜子是0.05的基础上增加了0.90,
∴1克的瓜子应在0.05的基础上增加了=,
∴x克瓜子的总售价为x+0.05,
故答案为c=x+0.05.
19.解:∵水龙头每秒钟会滴下2滴水,每滴水约0.05毫升,
∴离开x小时滴的水为3600×2×0.05x,
∴y=360x.(x≥0)
20.解:∵直线y=x﹣2与y轴的交点A的坐标为(0,﹣2),
∴A(0,﹣2),
∵图象经过点B(2,3),
∴3=2k﹣2,解得k=,
∴一次函数的解析式为y=x﹣2,
S△AOB=OA |xB|=×2×2=2.
21.解:设一次函数为y=kx+b(k≠0),(1分)
因为它的图象经过(3,5),(﹣4,﹣9),
所以
解得:,(3分)
所以这个一次函数为y=2x﹣1.(5分)
22.解:(1)由题意可得y﹣2=k(x+1),把当x=1时,y=5代入得:5﹣2=k(1+1),
解得:k=,
所以y﹣2=(x+1),
故一次函数的解析式为y=x+.
(2)当x=﹣3时,y=×(﹣3)+=﹣1.
23.解:(1)∵OB=2,
∴B(0,2),
代入y=x+b得,b=2,
∴一次函数的关系式为y=x+2;
(2)令y=0,则x+2=0,解得x=﹣6,
∴A(﹣6,0),
∴A△AOB=OA OB=×6×2=6,
∵S△OBC=,
∴S△OBC=3,
∴OC=3,
∴C(3,0)或(﹣3,0),
∴直线l的函数关系式为y=x+2或y=﹣x+2.
24.解:∵图象经过点A(﹣6,0),
∴0=﹣6k+b,
即b=6k①,
∵图象与y轴的交点是B(0,b),
∴ OB=12,
即:,
∴|b|=4,
∴b1=4,b2=﹣4,
代入①式,得,,
一次函数的表达式是或.
1.小明根据某个一次函数关系式填写了的表格:则空格中的数为( )
x ﹣1 0 2
y ﹣3 6
A.16 B.8 C.12 D.24
2.函数y=2x+b的图象与两坐标轴围成的三角形的面积为4,则函数的表达式为( )
A.y=2x+4 B.y=2x﹣4
C.y=2x+4或 y=2x﹣4 D.y=﹣2x﹣4
3.如图,直线l与y轴交于点(0,3),与正比例函数y=2x的图象交于点B,且B点的横坐标为1,则直线l对应函数的表达式是( )
A.y=x﹣3 B.y=2x+3 C.y=3﹣x D.y=x﹣3
4.如图,直线AB对应的函数表达式是( )
A.y=﹣x+3 B.y=x+3 C.y=﹣x+3 D.y=x+3
5.一块长为5米,宽为2米的长方形木板,现要在长边上截去长为x米的一小长方形(如图),则剩余木板的面积y(平方米)与x(米)之间的关系式为( )
A.y=2x B.y=10﹣2x C.y=5x D.y=10﹣5x
6.1千克某种水果5元,则所需钱数y(元)和水果重x(千克)之间的关系是( )
A.y=5x B.x=5y C. D.y=x+5
7.某水池现有水100m3,每小时进水20m3,排水15m3,t小时后水池中的水为Qm3,它的解析式为( )
A.Q=100+20t B.Q=100﹣15t C.Q=100+5t D.Q=100﹣5t
8.如果每盒圆珠笔有12支,售价18元,用y(元)表示圆珠笔的售价,x表示圆珠笔的支数,那么y与x之间的关系应该是( )
A.y=12x B.y=18x C.y=x D.y=x
9.如图所示,直线l的解析式是( )
A.y=x+2 B.y=﹣2x+2 C.y=x﹣2 D.y=﹣x﹣2
10.若直线y=kx+b经过点A(2,0),且与坐标轴围成的三角形的面积为6,则这条直线的表达式为 .
11.2021年1月1日,汽油价格为每升6.05元,张老师用一张面额为1000元的加油卡加油付费,则张老师卡上余额y(元)和加油量x(升)之间的函数关系式为 .
12.已知y是x的正比例函数,当x=1时y=﹣5,则当y=20时,x= .
13.若一次函数的图象经过点(0,﹣2),且与两坐标轴所围成的三角形面积为2,则这个函数的表达式为 .
14.若点P(﹣2,3)在直线y=﹣3x+b上,则b的值为 .
15.地面温度为15℃,在一定高度内如果高度每升高1千米,气温下降6℃.则气温t℃与高度h(千米)之间的关系式为 .
16.等腰三角形的周长为12厘米,底边长为y厘米,腰长为x厘米.则y与x的之间的关系式是y= (3<x<6).
17.某商店出售商品时,在进价的基础上又加了一定的利润,其数量x与售价y的关系如下表所示,那么售价y与数量x之间的关系式是 .
数量x(千克) 1 2 3 4 …
售价y(元) 8+0.4 16+0.8 24+1.2 32+1.6 …
18.商店出售一种瓜子数量x与售价c之间的关系如下表:
数量x(克) 售价c(元)
100 0.90+0.05
200 1.80+0.05
300 2.70+0.05
400 3.60+0.05
500 4.50+0 05
… …
(表内售价栏中的0.05是塑料袋的价钱)
则用含x的代数式表示c是 .
19.我国是一个严重缺水的国家,大家应倍加珍惜水资源,节约用水.据测试,拧不紧的水龙头每秒钟会滴下2滴水,每滴水约0.05毫升.小明同学在洗手后,没有把水龙头拧紧,当小明离开x小时后水龙头滴了y毫升水.试写出y关于x的函数关系式 .
20.在平面直角坐标系中,一次函数y=kx+b的图象(k≠0)与直线y=x﹣2相交于y轴上一点A,且图象经过点B(2,3)点O是坐标原点,求一次函数的解析式和△AOB的面积.
21.已知一次函数的图象过点(3,5)与点(﹣4,﹣9),求这个一次函数的解析式.
22.已知y﹣2与x+1成正比例函数,当x=1时,y=5.
(1)求y关于x的函数关系式;
(2)当x=﹣3时,求y的值.
23.如图,直线y=x+b与x轴交于点A,与y轴交于点B,且OB=2.
(1)求一次函数的关系式;
(2)若直线l过点B且与x轴交于点C,S△OBC=,求直线l的函数关系式.
24.已知一次函数y=kx+b的图象与x轴交于点A(﹣6,0),与y轴交于点B.若△AOB的面积为12,求一次函数的表达式.
参考答案
1.解:设一次函数的解析式为y=kx+b(k≠0),
∵x=﹣1时y=﹣3;x=0时,y=6,
∴,解得,
∴一次函数的解析式为y=9x+6,
∴当x=2时,y=18+6=24.
故选:D.
2.解:∵令x=0,则y=b,令y=0,则x=﹣,
∴函数y=2x+b的图象与两坐标轴的交点分别为(0,b),(﹣,0),
∴|b| |﹣|=4,解得b=±4,
∴函数的表达式为y=2x+4或y=2x﹣4.
故选:C.
3.解:设直线l对应函数的表达式为y=kx+b,
把x=1代入y=2x得y=2,则B点坐标为(1,2),
把B(1,2),(0,3)代入y=kx+b得,
解得,
所以直线l对应函数的表达式为y=﹣x+3.
故选:C.
4.解:设直线AB对应的函数表达式是y=kx+b,
把A(0,3),B(2,0)代入,
得,
解得,
故直线AB对应的函数表达式是y=﹣x+3.
故选:A.
5.解:由题意,有
y=2(5﹣x),
即y=10﹣2x.
故选:B.
6.解:设y=kx,然后根据题意列出关系式.
5=k 1,
∴k=5.
∴y=5x.
故选:A.
7.解:由题意得:Q=100+20t﹣15t=100+5t.
故选:C.
8.解:依题意有单价为18÷12=元,
则有y=x.
故选:D.
9.解:直线经过点(﹣2,0)和点(0,2),
因而可以设直线的解析式是y=k+b,
把点的坐标代入得到,
解得,
因而直线l的解析式是y=x+2.
故选:A.
10.解:把(2,0)代入得2k+b=0,解得b=﹣2k,
所以y=kx﹣2k,
把x=0代入得y=kx﹣2k得y=﹣2k,
所以直线与y轴的交点坐标为(0,﹣2k),
所以×2×|﹣2k|=6,解得k=3或﹣3,
所以所求的直线解析式为y=3x﹣6或y=﹣3x+6.
故答案为y=3x﹣6或y=﹣3x+6.
11.解:由题意得:
y与x的函数解析式为:y=1000﹣6.05x.
故答案为:y=1000﹣6.05x
12.解:设正比例函数的解析式为y=kx,
将x=1,y=﹣5代入,得﹣5=k,
所以y=﹣5x,
当y=20时,20=﹣5x,
解得x=﹣4.
故答案为﹣4.
13.解:由题意可设:y=kx﹣2,
与x轴交点为(,0),与y轴交点为(0,﹣2),
∴|| |﹣2|=2,
解得:k=1或﹣1,
∴函数解析式为y=x﹣2,或y=﹣x﹣2.
故答案是:y=x﹣2,或y=﹣x﹣2.
14.解:∵点P(﹣2,3)在直线y=﹣3x+b上,
∴点P(﹣2,3)满足直线y=﹣3x+b,
∴3=(﹣3)×(﹣2)+b
解得,b=﹣3;
故答案是:﹣3.
15.解:∵当高度为h时,降低6h,
∴气温t℃与高度h(千米)之间的关系式为 t=15﹣6h.
故答案为t=15﹣6h.
16.解:∵2x+y=12
∴y=﹣2x+12
∵x>6÷2=3,y<2x
∴3<x<6
即腰长y与底边x的函数关系是:y=﹣2x+12(3<x<6).
17.解:设y=kx,然后根据题意列出关系式.
8+0.4=k,
k=8.4.
∴y=8.4x.
故答案为:y=8.4x.
18.解:∵100克的瓜子是0.05的基础上增加了0.90,
∴1克的瓜子应在0.05的基础上增加了=,
∴x克瓜子的总售价为x+0.05,
故答案为c=x+0.05.
19.解:∵水龙头每秒钟会滴下2滴水,每滴水约0.05毫升,
∴离开x小时滴的水为3600×2×0.05x,
∴y=360x.(x≥0)
20.解:∵直线y=x﹣2与y轴的交点A的坐标为(0,﹣2),
∴A(0,﹣2),
∵图象经过点B(2,3),
∴3=2k﹣2,解得k=,
∴一次函数的解析式为y=x﹣2,
S△AOB=OA |xB|=×2×2=2.
21.解:设一次函数为y=kx+b(k≠0),(1分)
因为它的图象经过(3,5),(﹣4,﹣9),
所以
解得:,(3分)
所以这个一次函数为y=2x﹣1.(5分)
22.解:(1)由题意可得y﹣2=k(x+1),把当x=1时,y=5代入得:5﹣2=k(1+1),
解得:k=,
所以y﹣2=(x+1),
故一次函数的解析式为y=x+.
(2)当x=﹣3时,y=×(﹣3)+=﹣1.
23.解:(1)∵OB=2,
∴B(0,2),
代入y=x+b得,b=2,
∴一次函数的关系式为y=x+2;
(2)令y=0,则x+2=0,解得x=﹣6,
∴A(﹣6,0),
∴A△AOB=OA OB=×6×2=6,
∵S△OBC=,
∴S△OBC=3,
∴OC=3,
∴C(3,0)或(﹣3,0),
∴直线l的函数关系式为y=x+2或y=﹣x+2.
24.解:∵图象经过点A(﹣6,0),
∴0=﹣6k+b,
即b=6k①,
∵图象与y轴的交点是B(0,b),
∴ OB=12,
即:,
∴|b|=4,
∴b1=4,b2=﹣4,
代入①式,得,,
一次函数的表达式是或.
