2021-2022学年人教版八年级数学下册17.2 勾股定理的逆定理 常考题套卷 (word版 含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册17.2 勾股定理的逆定理 常考题套卷 (word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 183.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 14:24:45 | ||
图片预览



文档简介
2021年人教新版八年级(下)《17.2 勾股定理的逆定理》常考题套卷(5)
一、选择题(共10小题)
1.三角形的三边长分别为6,8,10,它的最长边上的高为( )
A.6 B.2.4 C.8 D.4.8
2.一架25米长的云梯,斜立在一竖直的墙上,这时梯脚距离墙底端7米.如果梯子的顶端沿墙下滑4米,那么梯脚将水平滑动( )
A.9米 B.15米 C.5米 D.8米
3.在下列长度的各组线段中,能组成直角三角形的是( )
A.5,6,7 B.1,4,8 C.5,12,13 D.5,11,12
4.下列各组数中不能作为直角三角形的三边长的是( )
A.1.5,2,3 B.7,24,25 C.6,8,10 D.9,12,15
5.放学以后,小红和小颖从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是200米/分,小红用3分钟到家,小颖4分钟到家,小红和小颖家的直线距离为( )
A.600米 B.800米 C.1000米 D.1400米
6.下列各组数能构成勾股数的是( )
A.2,, B.12,16,20 C.,, D.32,42,52
7.下列各比值中,是直角三角形的三边之比的是( )
A.1:2:3 B.2:3:4 C.3:4:6 D.1::2
8.在下列长度的各组线段中,不能构成直角三角形的是( )
A.3,4,5 B.7,24,25 C.1,1, D.,,
9.若线段a,b,c能构成直角三角形,则它们的比为( )
A.2:3:4 B.3:4:6 C.5:12:13 D.4:6:7
10.下列各组数中能够作为直角三角形的三边长的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
二、填空题(共5小题)
11.小明想知道学校旗杆有多高,他发现旗杆上的绳子垂到地面还余1m,当他把绳子下端拉开5m后,发现下端刚好接触地面,则旗杆高度为 米.
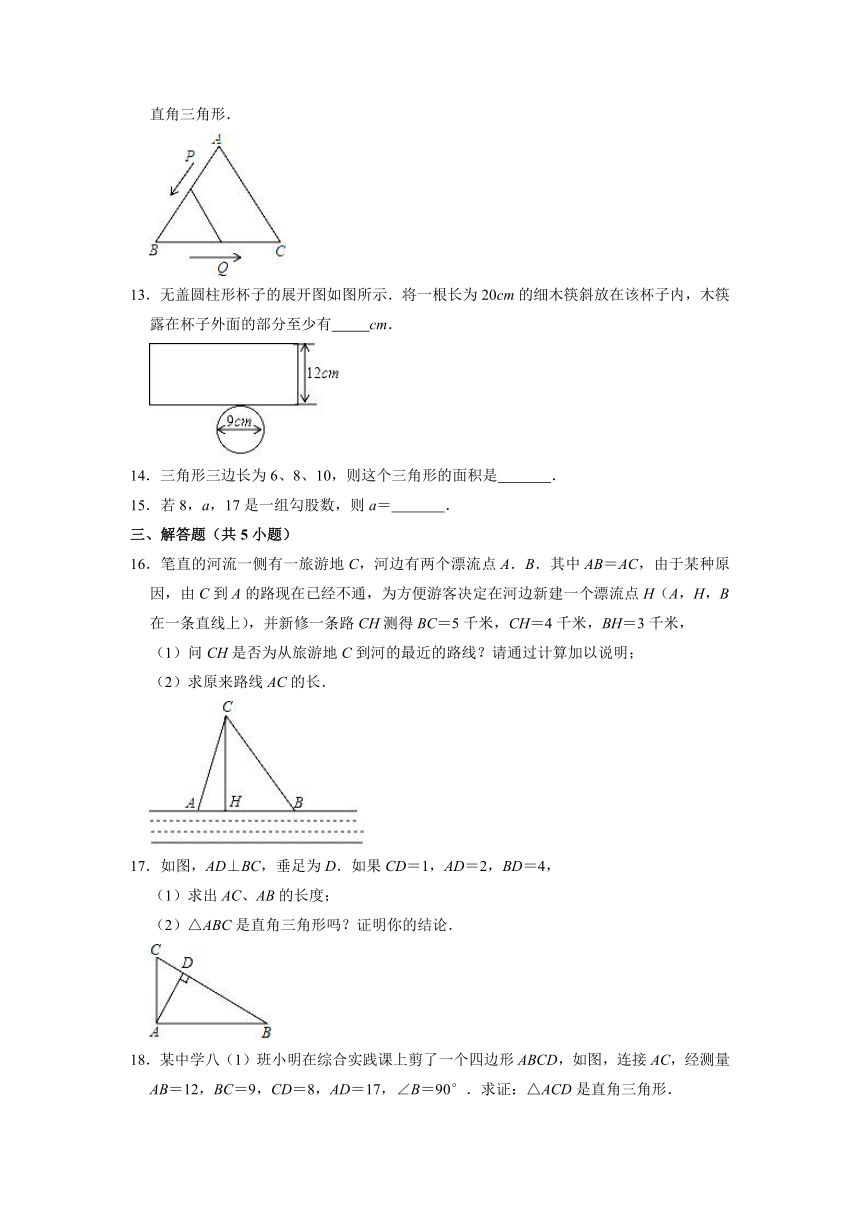
12.如图,△ABC是边长为6cm的等边三角形,动点P,Q同时从A,B两点出发,分别在AB,BC边上匀速移动,它们的速度分别为2cm/s和1cm/s,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为ts,则当t= s时,△PBQ为直角三角形.
13.无盖圆柱形杯子的展开图如图所示.将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 cm.
14.三角形三边长为6、8、10,则这个三角形的面积是 .
15.若8,a,17是一组勾股数,则a= .
三、解答题(共5小题)
16.笔直的河流一侧有一旅游地C,河边有两个漂流点A.B.其中AB=AC,由于某种原因,由C到A的路现在已经不通,为方便游客决定在河边新建一个漂流点H(A,H,B在一条直线上),并新修一条路CH测得BC=5千米,CH=4千米,BH=3千米,
(1)问CH是否为从旅游地C到河的最近的路线?请通过计算加以说明;
(2)求原来路线AC的长.
17.如图,AD⊥BC,垂足为D.如果CD=1,AD=2,BD=4,
(1)求出AC、AB的长度;
(2)△ABC是直角三角形吗?证明你的结论.
18.某中学八(1)班小明在综合实践课上剪了一个四边形ABCD,如图,连接AC,经测量AB=12,BC=9,CD=8,AD=17,∠B=90°.求证:△ACD是直角三角形.
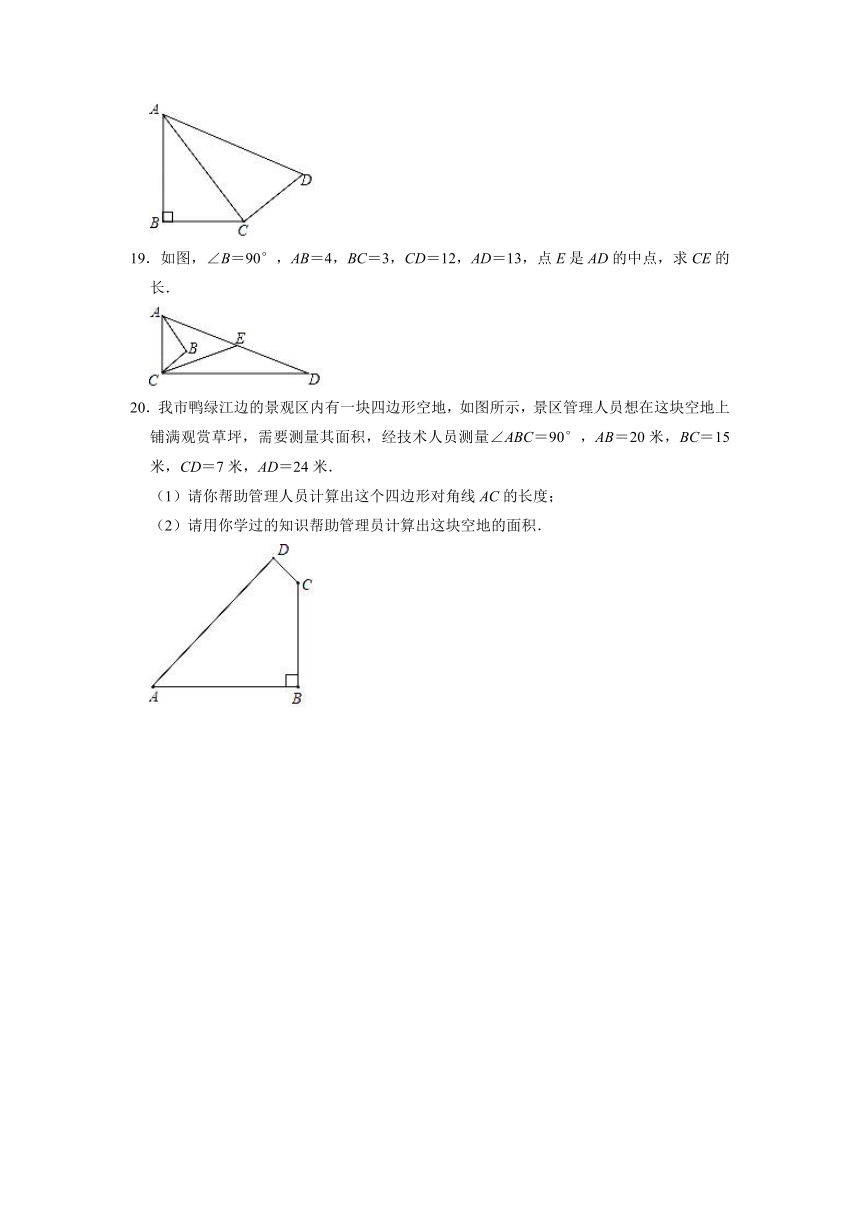
19.如图,∠B=90°,AB=4,BC=3,CD=12,AD=13,点E是AD的中点,求CE的长.
20.我市鸭绿江边的景观区内有一块四边形空地,如图所示,景区管理人员想在这块空地上铺满观赏草坪,需要测量其面积,经技术人员测量∠ABC=90°,AB=20米,BC=15米,CD=7米,AD=24米.
(1)请你帮助管理人员计算出这个四边形对角线AC的长度;
(2)请用你学过的知识帮助管理员计算出这块空地的面积.
2021年人教新版八年级(下)《17.2 勾股定理的逆定理》常考题套卷(5)
参考答案与试题解析
一、选择题(共10小题)
1.三角形的三边长分别为6,8,10,它的最长边上的高为( )
A.6 B.2.4 C.8 D.4.8
【解答】解:∵三角形的三边长分别为6,8,10,符合勾股定理的逆定理62+82=102,
∴此三角形为直角三角形,则10为直角三角形的斜边,
设三角形最长边上的高是h,
根据三角形的面积公式得:×6×8=×10h,
解得h=4.8.
故选:D.
2.一架25米长的云梯,斜立在一竖直的墙上,这时梯脚距离墙底端7米.如果梯子的顶端沿墙下滑4米,那么梯脚将水平滑动( )
A.9米 B.15米 C.5米 D.8米
【解答】解:梯子顶端距离墙角地距离为=24m,
顶端下滑后梯子底端距离墙角的距离为=15m,
15m﹣7m=8m.
故选:D.
3.在下列长度的各组线段中,能组成直角三角形的是( )
A.5,6,7 B.1,4,8 C.5,12,13 D.5,11,12
【解答】解:A、因为52+62≠72,所以不能组成直角三角形;
B、因为12+42≠82,所以不能组成直角三角形;
C、因为52+122=132,所以能组成直角三角形;
D、因为52+112≠122,所以不能组成直角三角形.
故选:C.
4.下列各组数中不能作为直角三角形的三边长的是( )
A.1.5,2,3 B.7,24,25 C.6,8,10 D.9,12,15
【解答】解:A、1.52+22≠32,不符合勾股定理的逆定理,故正确;
B、72+242=252,符合勾股定理的逆定理,故错误;
C、62+82=102,符合勾股定理的逆定理,故错误;
D、92+122=152,符合勾股定理的逆定理,故错误.
故选:A.
5.放学以后,小红和小颖从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是200米/分,小红用3分钟到家,小颖4分钟到家,小红和小颖家的直线距离为( )
A.600米 B.800米 C.1000米 D.1400米
【解答】解:根据题意得:如图:
OA=3×200=600m.
OB=4×200=800m.
在直角△OAB中,AB==1000米.
故选:C.
6.下列各组数能构成勾股数的是( )
A.2,, B.12,16,20 C.,, D.32,42,52
【解答】解:A、22+()2=()2,但不是正整数,故选项错误;
B、122+162=202,能构成直角三角形,是整数,故选项正确;
C、()2+()2≠()2,不能构成直角三角形,故选项错误;
D、(32)2+(42)2≠(52)2,不能构成直角三角形,故选项错误.
故选:B.
7.下列各比值中,是直角三角形的三边之比的是( )
A.1:2:3 B.2:3:4 C.3:4:6 D.1::2
【解答】解:A、∵x+2x=3x,∴三条线段不能组成三角形,不能组成直角三角形,故A选项错误;
B、∵(2x)2+(3x)2≠(4x)2,∴三条线段不能组成直角三角形,故B选项错误;
C、∵(3x)2+(4x)2≠(6x)2,∴三条线段不能组成直角三角形,故C选项错误;
D、∵x2+(x)2=(2x)2,∴三条线段能组成直角三角形,故D选项正确;
故选:D.
8.在下列长度的各组线段中,不能构成直角三角形的是( )
A.3,4,5 B.7,24,25 C.1,1, D.,,
【解答】解:A、∵32+42=52,∴能构成直角三角形;
B、∵72+242=252,∴能构成直角三角形;
C、∵12+12=()2,∴能构成直角三角形.
D、∵()2+()2≠()2,∴不能构成直角三角形;
故选:D.
9.若线段a,b,c能构成直角三角形,则它们的比为( )
A.2:3:4 B.3:4:6 C.5:12:13 D.4:6:7
【解答】解:A、22+32≠42,不能构成直角三角形,故错误;
B、32+42≠62,不能构成直角三角形,故错误;
C、52+122=132,能构成直角三角形,故正确;
D、42+62≠72,不能构成直角三角形,故错误.
故选:C.
10.下列各组数中能够作为直角三角形的三边长的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
【解答】解:A、12+22≠32,不能构成直角三角形,故此选项错误;
B、22+32≠42,不能构成直角三角形,故此选项错误;
C、32+42=52,能构成直角三角形,故此选项正确;
D、42+52≠62,不能构成直角三角形,故此选项错误.
故选:C.
二、填空题(共5小题)
11.小明想知道学校旗杆有多高,他发现旗杆上的绳子垂到地面还余1m,当他把绳子下端拉开5m后,发现下端刚好接触地面,则旗杆高度为 12 米.
【解答】解:设旗杆高xm,则绳子长为(x+1)m,∵旗杆垂直于地面,
∴旗杆,绳子与地面构成直角三角形,由题意列式为x2+52=(x+1)2,解得x=12m.
12.如图,△ABC是边长为6cm的等边三角形,动点P,Q同时从A,B两点出发,分别在AB,BC边上匀速移动,它们的速度分别为2cm/s和1cm/s,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为ts,则当t= 或 s时,△PBQ为直角三角形.
【解答】解:∵△ABC是等边三角形,
∴AB=BC=6cm,∠A=∠B=∠C=60°,
当∠PQB=90°时,∠BPQ=30°,
∴BP=2BQ.
∵BP=6﹣2x,BQ=x,
∴6﹣2x=2x,
解得x=;
当∠QPB=90°时,∠PQB=30°,
∴BQ=2PB,
∴x=2(6﹣2x),
解得x=.
答:或秒时,△BPQ是直角三角形.
故答案为或.
13.无盖圆柱形杯子的展开图如图所示.将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 5 cm.
【解答】解:由题意可得:
杯子内的筷子长度为:=15(cm),
则筷子露在杯子外面的筷子长度为:20﹣15=5(cm).
故答案为:5.
14.三角形三边长为6、8、10,则这个三角形的面积是 24 .
【解答】解:∵三角形的三边长分别为6、8、10,
而62+82=102,
∴此三角形是直角三角形,
∴S△=×6×8=24.
15.若8,a,17是一组勾股数,则a= 15 .
【解答】解:①a为最长边,a=,不是正整数,不符合题意;
②17为最长边,a==15,三边是整数,能构成勾股数,符合题意.
故答案为:15.
三、解答题(共5小题)
16.笔直的河流一侧有一旅游地C,河边有两个漂流点A.B.其中AB=AC,由于某种原因,由C到A的路现在已经不通,为方便游客决定在河边新建一个漂流点H(A,H,B在一条直线上),并新修一条路CH测得BC=5千米,CH=4千米,BH=3千米,
(1)问CH是否为从旅游地C到河的最近的路线?请通过计算加以说明;
(2)求原来路线AC的长.
【解答】解:(1)CH是从旅游地C到河的最近的路线,
理由是:在△CHB中,
∵CH2+BH2=42+32=25,
BC2=25,
∴CH2+BH2=BC2
∴△HBC是直角三角形且∠CHB=90°,
∴CH⊥AB,
所以CH是从旅游地C到河的最近的路线;
(2)设AC=AB=x千米,则AH=(x﹣3)千米,
在Rt△ACH中,由已知得AC=x,AH=x﹣3,CH=4,
由勾股定理得:AC2=AH2+CH2
∴x2=(x﹣3)2+42
解这个方程,得x=,
答:原来的路线AC的长为千米.
17.如图,AD⊥BC,垂足为D.如果CD=1,AD=2,BD=4,
(1)求出AC、AB的长度;
(2)△ABC是直角三角形吗?证明你的结论.
【解答】解:(1)∵CD=1,AD=2,BD=4,AD⊥BC,
∴AC=;AB=2
(2)∵AC=;AB=2,BC=CD+BD=5,
∴AC2+AB2=BC2,
∴△ABC是直角三角形.
18.某中学八(1)班小明在综合实践课上剪了一个四边形ABCD,如图,连接AC,经测量AB=12,BC=9,CD=8,AD=17,∠B=90°.求证:△ACD是直角三角形.
【解答】证明:∵∠B=90°,AB=12,BC=9,
∴AC2=AB2+BC2=144+81=225,
∴AC=15,
又∵AC2+CD2=225+64=289,AD2=289,
∴AC2+CD2=AD2,
∴△ACD是直角三角形.
19.如图,∠B=90°,AB=4,BC=3,CD=12,AD=13,点E是AD的中点,求CE的长.
【解答】解:在Rt△ABC中,∠B=90°,
∵AB=3,BC=4,
∴,
∵CD=12,AD=13,
∵AC2+CD2=52+122=169,
AD2=169,
∴AC2+CD2=AD2,
∴∠C=90°,
∴△ACD是直角三角形,
∵点E是AD的中点,
∴CE=.
20.我市鸭绿江边的景观区内有一块四边形空地,如图所示,景区管理人员想在这块空地上铺满观赏草坪,需要测量其面积,经技术人员测量∠ABC=90°,AB=20米,BC=15米,CD=7米,AD=24米.
(1)请你帮助管理人员计算出这个四边形对角线AC的长度;
(2)请用你学过的知识帮助管理员计算出这块空地的面积.
【解答】解:(1)连接AC.
在Rt△ABC中,∵∠ABC=90°,AB=20,BC=15,
∴AC===25(米).
∴这个四边形对角线AC的长度为25米.
(2)在△ADC中,∵CD=7,AD=24,AC=25,
∴AD2+CD2=242+72=252=AC2,
∴△ADC为直角三角形,∠ADC=90°,
∴S四边形ABCD=S△ADC+S△ABC=×15×20+×7×24=234(平方米),
∴四边形ABCD的面积为234平方米.
一、选择题(共10小题)
1.三角形的三边长分别为6,8,10,它的最长边上的高为( )
A.6 B.2.4 C.8 D.4.8
2.一架25米长的云梯,斜立在一竖直的墙上,这时梯脚距离墙底端7米.如果梯子的顶端沿墙下滑4米,那么梯脚将水平滑动( )
A.9米 B.15米 C.5米 D.8米
3.在下列长度的各组线段中,能组成直角三角形的是( )
A.5,6,7 B.1,4,8 C.5,12,13 D.5,11,12
4.下列各组数中不能作为直角三角形的三边长的是( )
A.1.5,2,3 B.7,24,25 C.6,8,10 D.9,12,15
5.放学以后,小红和小颖从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是200米/分,小红用3分钟到家,小颖4分钟到家,小红和小颖家的直线距离为( )
A.600米 B.800米 C.1000米 D.1400米
6.下列各组数能构成勾股数的是( )
A.2,, B.12,16,20 C.,, D.32,42,52
7.下列各比值中,是直角三角形的三边之比的是( )
A.1:2:3 B.2:3:4 C.3:4:6 D.1::2
8.在下列长度的各组线段中,不能构成直角三角形的是( )
A.3,4,5 B.7,24,25 C.1,1, D.,,
9.若线段a,b,c能构成直角三角形,则它们的比为( )
A.2:3:4 B.3:4:6 C.5:12:13 D.4:6:7
10.下列各组数中能够作为直角三角形的三边长的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
二、填空题(共5小题)
11.小明想知道学校旗杆有多高,他发现旗杆上的绳子垂到地面还余1m,当他把绳子下端拉开5m后,发现下端刚好接触地面,则旗杆高度为 米.
12.如图,△ABC是边长为6cm的等边三角形,动点P,Q同时从A,B两点出发,分别在AB,BC边上匀速移动,它们的速度分别为2cm/s和1cm/s,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为ts,则当t= s时,△PBQ为直角三角形.
13.无盖圆柱形杯子的展开图如图所示.将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 cm.
14.三角形三边长为6、8、10,则这个三角形的面积是 .
15.若8,a,17是一组勾股数,则a= .
三、解答题(共5小题)
16.笔直的河流一侧有一旅游地C,河边有两个漂流点A.B.其中AB=AC,由于某种原因,由C到A的路现在已经不通,为方便游客决定在河边新建一个漂流点H(A,H,B在一条直线上),并新修一条路CH测得BC=5千米,CH=4千米,BH=3千米,
(1)问CH是否为从旅游地C到河的最近的路线?请通过计算加以说明;
(2)求原来路线AC的长.
17.如图,AD⊥BC,垂足为D.如果CD=1,AD=2,BD=4,
(1)求出AC、AB的长度;
(2)△ABC是直角三角形吗?证明你的结论.
18.某中学八(1)班小明在综合实践课上剪了一个四边形ABCD,如图,连接AC,经测量AB=12,BC=9,CD=8,AD=17,∠B=90°.求证:△ACD是直角三角形.
19.如图,∠B=90°,AB=4,BC=3,CD=12,AD=13,点E是AD的中点,求CE的长.
20.我市鸭绿江边的景观区内有一块四边形空地,如图所示,景区管理人员想在这块空地上铺满观赏草坪,需要测量其面积,经技术人员测量∠ABC=90°,AB=20米,BC=15米,CD=7米,AD=24米.
(1)请你帮助管理人员计算出这个四边形对角线AC的长度;
(2)请用你学过的知识帮助管理员计算出这块空地的面积.
2021年人教新版八年级(下)《17.2 勾股定理的逆定理》常考题套卷(5)
参考答案与试题解析
一、选择题(共10小题)
1.三角形的三边长分别为6,8,10,它的最长边上的高为( )
A.6 B.2.4 C.8 D.4.8
【解答】解:∵三角形的三边长分别为6,8,10,符合勾股定理的逆定理62+82=102,
∴此三角形为直角三角形,则10为直角三角形的斜边,
设三角形最长边上的高是h,
根据三角形的面积公式得:×6×8=×10h,
解得h=4.8.
故选:D.
2.一架25米长的云梯,斜立在一竖直的墙上,这时梯脚距离墙底端7米.如果梯子的顶端沿墙下滑4米,那么梯脚将水平滑动( )
A.9米 B.15米 C.5米 D.8米
【解答】解:梯子顶端距离墙角地距离为=24m,
顶端下滑后梯子底端距离墙角的距离为=15m,
15m﹣7m=8m.
故选:D.
3.在下列长度的各组线段中,能组成直角三角形的是( )
A.5,6,7 B.1,4,8 C.5,12,13 D.5,11,12
【解答】解:A、因为52+62≠72,所以不能组成直角三角形;
B、因为12+42≠82,所以不能组成直角三角形;
C、因为52+122=132,所以能组成直角三角形;
D、因为52+112≠122,所以不能组成直角三角形.
故选:C.
4.下列各组数中不能作为直角三角形的三边长的是( )
A.1.5,2,3 B.7,24,25 C.6,8,10 D.9,12,15
【解答】解:A、1.52+22≠32,不符合勾股定理的逆定理,故正确;
B、72+242=252,符合勾股定理的逆定理,故错误;
C、62+82=102,符合勾股定理的逆定理,故错误;
D、92+122=152,符合勾股定理的逆定理,故错误.
故选:A.
5.放学以后,小红和小颖从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是200米/分,小红用3分钟到家,小颖4分钟到家,小红和小颖家的直线距离为( )
A.600米 B.800米 C.1000米 D.1400米
【解答】解:根据题意得:如图:
OA=3×200=600m.
OB=4×200=800m.
在直角△OAB中,AB==1000米.
故选:C.
6.下列各组数能构成勾股数的是( )
A.2,, B.12,16,20 C.,, D.32,42,52
【解答】解:A、22+()2=()2,但不是正整数,故选项错误;
B、122+162=202,能构成直角三角形,是整数,故选项正确;
C、()2+()2≠()2,不能构成直角三角形,故选项错误;
D、(32)2+(42)2≠(52)2,不能构成直角三角形,故选项错误.
故选:B.
7.下列各比值中,是直角三角形的三边之比的是( )
A.1:2:3 B.2:3:4 C.3:4:6 D.1::2
【解答】解:A、∵x+2x=3x,∴三条线段不能组成三角形,不能组成直角三角形,故A选项错误;
B、∵(2x)2+(3x)2≠(4x)2,∴三条线段不能组成直角三角形,故B选项错误;
C、∵(3x)2+(4x)2≠(6x)2,∴三条线段不能组成直角三角形,故C选项错误;
D、∵x2+(x)2=(2x)2,∴三条线段能组成直角三角形,故D选项正确;
故选:D.
8.在下列长度的各组线段中,不能构成直角三角形的是( )
A.3,4,5 B.7,24,25 C.1,1, D.,,
【解答】解:A、∵32+42=52,∴能构成直角三角形;
B、∵72+242=252,∴能构成直角三角形;
C、∵12+12=()2,∴能构成直角三角形.
D、∵()2+()2≠()2,∴不能构成直角三角形;
故选:D.
9.若线段a,b,c能构成直角三角形,则它们的比为( )
A.2:3:4 B.3:4:6 C.5:12:13 D.4:6:7
【解答】解:A、22+32≠42,不能构成直角三角形,故错误;
B、32+42≠62,不能构成直角三角形,故错误;
C、52+122=132,能构成直角三角形,故正确;
D、42+62≠72,不能构成直角三角形,故错误.
故选:C.
10.下列各组数中能够作为直角三角形的三边长的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
【解答】解:A、12+22≠32,不能构成直角三角形,故此选项错误;
B、22+32≠42,不能构成直角三角形,故此选项错误;
C、32+42=52,能构成直角三角形,故此选项正确;
D、42+52≠62,不能构成直角三角形,故此选项错误.
故选:C.
二、填空题(共5小题)
11.小明想知道学校旗杆有多高,他发现旗杆上的绳子垂到地面还余1m,当他把绳子下端拉开5m后,发现下端刚好接触地面,则旗杆高度为 12 米.
【解答】解:设旗杆高xm,则绳子长为(x+1)m,∵旗杆垂直于地面,
∴旗杆,绳子与地面构成直角三角形,由题意列式为x2+52=(x+1)2,解得x=12m.
12.如图,△ABC是边长为6cm的等边三角形,动点P,Q同时从A,B两点出发,分别在AB,BC边上匀速移动,它们的速度分别为2cm/s和1cm/s,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为ts,则当t= 或 s时,△PBQ为直角三角形.
【解答】解:∵△ABC是等边三角形,
∴AB=BC=6cm,∠A=∠B=∠C=60°,
当∠PQB=90°时,∠BPQ=30°,
∴BP=2BQ.
∵BP=6﹣2x,BQ=x,
∴6﹣2x=2x,
解得x=;
当∠QPB=90°时,∠PQB=30°,
∴BQ=2PB,
∴x=2(6﹣2x),
解得x=.
答:或秒时,△BPQ是直角三角形.
故答案为或.
13.无盖圆柱形杯子的展开图如图所示.将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 5 cm.
【解答】解:由题意可得:
杯子内的筷子长度为:=15(cm),
则筷子露在杯子外面的筷子长度为:20﹣15=5(cm).
故答案为:5.
14.三角形三边长为6、8、10,则这个三角形的面积是 24 .
【解答】解:∵三角形的三边长分别为6、8、10,
而62+82=102,
∴此三角形是直角三角形,
∴S△=×6×8=24.
15.若8,a,17是一组勾股数,则a= 15 .
【解答】解:①a为最长边,a=,不是正整数,不符合题意;
②17为最长边,a==15,三边是整数,能构成勾股数,符合题意.
故答案为:15.
三、解答题(共5小题)
16.笔直的河流一侧有一旅游地C,河边有两个漂流点A.B.其中AB=AC,由于某种原因,由C到A的路现在已经不通,为方便游客决定在河边新建一个漂流点H(A,H,B在一条直线上),并新修一条路CH测得BC=5千米,CH=4千米,BH=3千米,
(1)问CH是否为从旅游地C到河的最近的路线?请通过计算加以说明;
(2)求原来路线AC的长.
【解答】解:(1)CH是从旅游地C到河的最近的路线,
理由是:在△CHB中,
∵CH2+BH2=42+32=25,
BC2=25,
∴CH2+BH2=BC2
∴△HBC是直角三角形且∠CHB=90°,
∴CH⊥AB,
所以CH是从旅游地C到河的最近的路线;
(2)设AC=AB=x千米,则AH=(x﹣3)千米,
在Rt△ACH中,由已知得AC=x,AH=x﹣3,CH=4,
由勾股定理得:AC2=AH2+CH2
∴x2=(x﹣3)2+42
解这个方程,得x=,
答:原来的路线AC的长为千米.
17.如图,AD⊥BC,垂足为D.如果CD=1,AD=2,BD=4,
(1)求出AC、AB的长度;
(2)△ABC是直角三角形吗?证明你的结论.
【解答】解:(1)∵CD=1,AD=2,BD=4,AD⊥BC,
∴AC=;AB=2
(2)∵AC=;AB=2,BC=CD+BD=5,
∴AC2+AB2=BC2,
∴△ABC是直角三角形.
18.某中学八(1)班小明在综合实践课上剪了一个四边形ABCD,如图,连接AC,经测量AB=12,BC=9,CD=8,AD=17,∠B=90°.求证:△ACD是直角三角形.
【解答】证明:∵∠B=90°,AB=12,BC=9,
∴AC2=AB2+BC2=144+81=225,
∴AC=15,
又∵AC2+CD2=225+64=289,AD2=289,
∴AC2+CD2=AD2,
∴△ACD是直角三角形.
19.如图,∠B=90°,AB=4,BC=3,CD=12,AD=13,点E是AD的中点,求CE的长.
【解答】解:在Rt△ABC中,∠B=90°,
∵AB=3,BC=4,
∴,
∵CD=12,AD=13,
∵AC2+CD2=52+122=169,
AD2=169,
∴AC2+CD2=AD2,
∴∠C=90°,
∴△ACD是直角三角形,
∵点E是AD的中点,
∴CE=.
20.我市鸭绿江边的景观区内有一块四边形空地,如图所示,景区管理人员想在这块空地上铺满观赏草坪,需要测量其面积,经技术人员测量∠ABC=90°,AB=20米,BC=15米,CD=7米,AD=24米.
(1)请你帮助管理人员计算出这个四边形对角线AC的长度;
(2)请用你学过的知识帮助管理员计算出这块空地的面积.
【解答】解:(1)连接AC.
在Rt△ABC中,∵∠ABC=90°,AB=20,BC=15,
∴AC===25(米).
∴这个四边形对角线AC的长度为25米.
(2)在△ADC中,∵CD=7,AD=24,AC=25,
∴AD2+CD2=242+72=252=AC2,
∴△ADC为直角三角形,∠ADC=90°,
∴S四边形ABCD=S△ADC+S△ABC=×15×20+×7×24=234(平方米),
∴四边形ABCD的面积为234平方米.
