中考数学 直角三角形 二轮复习课 教案设计与反思
文档属性
| 名称 | 中考数学 直角三角形 二轮复习课 教案设计与反思 |  | |
| 格式 | zip | ||
| 文件大小 | 110.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 19:10:04 | ||
图片预览

文档简介
授课人 备课时间 12.9 上课时间 4.15
执教班级 课 题 直角三角形
教学课时 1 教学课型(新授、复习、习题、实验等) 复习
教学目标 与能力知识:掌握直角三角形的性质和判定、逆命题和逆定理、勾股定理及逆定理、角平分线的性质、线段的中垂线及其性质过程与方法:了解逆命题和逆定理的概念;掌握直角三角形中两锐角互余、斜边上的中线等于斜边的一半及30°角所对的直角边等于斜边的一半等性质,掌握勾股定理及其逆定理,并能运用它们进行简单的论证和计算;掌握角平分线的性质定理及其逆定理,线段中垂线性质定理及其逆定理情感态度与价值观:(1)培养学生理论联系实际的思想(2)加强学生之间互帮互助团结合作的精神
教学重点、难点 重点:直角三角形性质及其判定的应用,难点:角平分线性质定理及其逆定理,线段中垂线的性质定理及其逆定理的应用,逆命题的概念,
媒体运用 华为智慧云课堂
预设过程(应包括课程导入、预习自学、展示交流、当堂练习检测等)
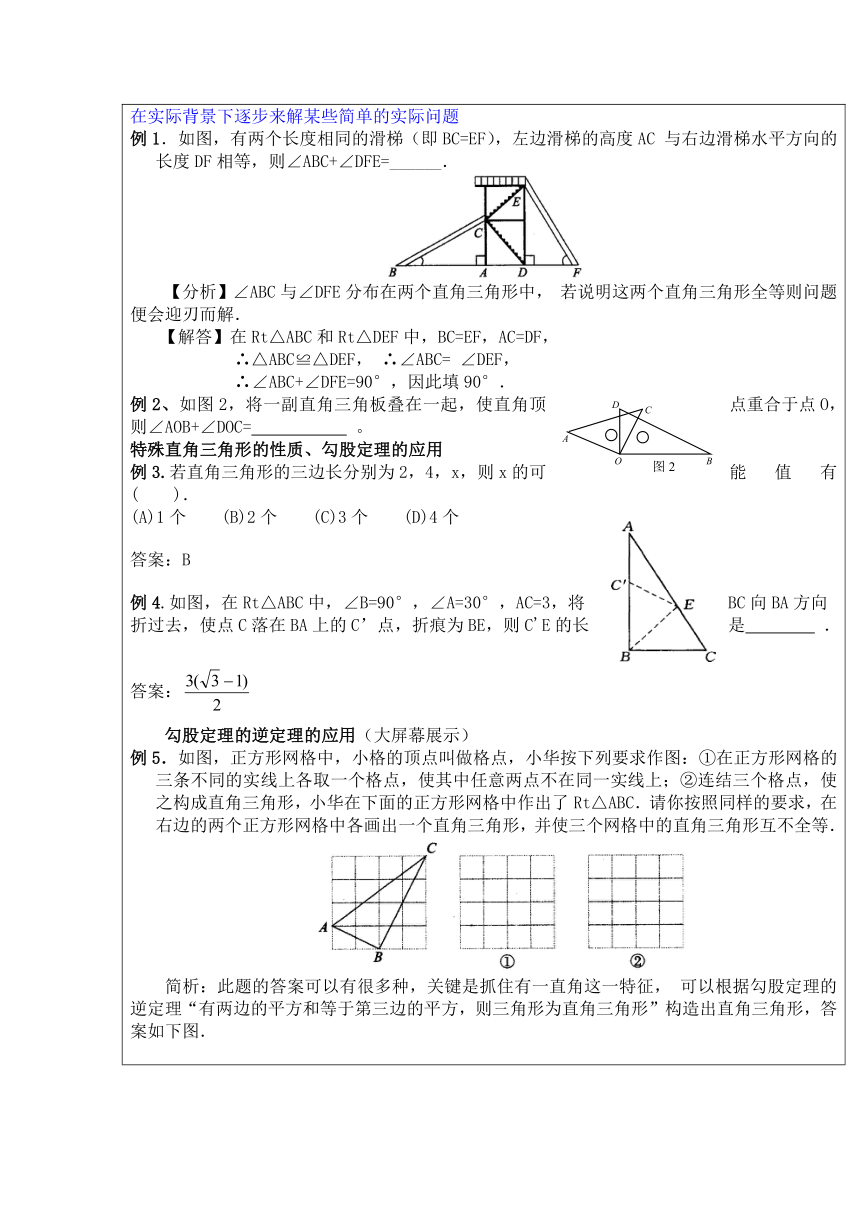
【回顾与思考】 直角三角形〖考查重点与常见题型〗中考题中多为选择题或填空题,有时也考查中档的解答题,如:在直角三角形中,已知一条直角边的长为6,斜边上的中线长为5,则另一条直角边的长为 命题“平行四边形的对角线互相平分”的逆命题是 在△ABC中,如果∠A-∠B=90°,那么△ABC是( ) (A)直角三角形(B)锐角三角形(C)钝角三角形(D)锐角三角形或钝角三角形【例题经典】直角三角形两锐角互余(大屏幕展示)理解直角三角形中边角之间的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,并会用解直角三角形的有关知识,在实际背景下逐步来解某些简单的实际问题例1.如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=______. 【分析】∠ABC与∠DFE分布在两个直角三角形中,若说明这两个直角三角形全等则问题便会迎刃而解.【解答】在Rt△ABC和Rt△DEF中,BC=EF,AC=DF,∴△ABC≌△DEF,∴∠ABC=∠DEF,∴∠ABC+∠DFE=90°,因此填90°.例2、如图2,将一副直角三角板叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC= 。特殊直角三角形的性质、勾股定理的应用例3.若直角三角形的三边长分别为2,4,x,则x的可能值有( ).(A)1个 (B)2个 (C)3个 (D)4个答案:B例4.如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=3,将BC向BA方向折过去,使点C落在BA上的C’点,折痕为BE,则C'E的长是 .答案: 勾股定理的逆定理的应用(大屏幕展示)例5.如图,正方形网格中,小格的顶点叫做格点,小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一实线上;②连结三个格点,使之构成直角三角形,小华在下面的正方形网格中作出了Rt△ABC.请你按照同样的要求,在右边的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形互不全等. 简析:此题的答案可以有很多种,关键是抓住有一直角这一特征,可以根据勾股定理的逆定理“有两边的平方和等于第三边的平方,则三角形为直角三角形”构造出直角三角形,答案如下图.练习:1.已知,如图所示,折叠长方形的一边AD,使点D落在BC边的点F处,如果AB=8cm,BC=10cm,(1)求EC的长;(2)在线段BC上还能找到点P使∠APE=90°吗,求出此时的BP长.2.如图,在梯形中,,,,于点,,,求BE的长度.3.如图,一块四边形土地,其中m,m,求这块土地的面积【作业设计】 集锦 必做:1选做:2
板书设计 【回顾与思考】 直角三角形
教学后记或反思(主要记录课堂设计理念,实际教学效果及改进设想等)
通过对近三年的中考题以及期末统考题进行了分析,发现主要考查的是直角三角形的应用问题。课时比较紧张,为了更好的让学生多得分,我在整整一节课中关注的基本都是直角三角形的应用问题,忽略了各层次学生的基本情况。一开始虽然有几道“基础”题,但都是与实际相结合的问题,学生上来就做这些题,中等层次以下的学生会找不到解决问题的钥匙,从而产生恐惧感。我结合了自己的教学风格以及任教班级学生的特点,对教案作深入的推敲、斟酌,调整了教学方式以及一部分题目。
图2
A
D
E
C
B
执教班级 课 题 直角三角形
教学课时 1 教学课型(新授、复习、习题、实验等) 复习
教学目标 与能力知识:掌握直角三角形的性质和判定、逆命题和逆定理、勾股定理及逆定理、角平分线的性质、线段的中垂线及其性质过程与方法:了解逆命题和逆定理的概念;掌握直角三角形中两锐角互余、斜边上的中线等于斜边的一半及30°角所对的直角边等于斜边的一半等性质,掌握勾股定理及其逆定理,并能运用它们进行简单的论证和计算;掌握角平分线的性质定理及其逆定理,线段中垂线性质定理及其逆定理情感态度与价值观:(1)培养学生理论联系实际的思想(2)加强学生之间互帮互助团结合作的精神
教学重点、难点 重点:直角三角形性质及其判定的应用,难点:角平分线性质定理及其逆定理,线段中垂线的性质定理及其逆定理的应用,逆命题的概念,
媒体运用 华为智慧云课堂
预设过程(应包括课程导入、预习自学、展示交流、当堂练习检测等)
【回顾与思考】 直角三角形〖考查重点与常见题型〗中考题中多为选择题或填空题,有时也考查中档的解答题,如:在直角三角形中,已知一条直角边的长为6,斜边上的中线长为5,则另一条直角边的长为 命题“平行四边形的对角线互相平分”的逆命题是 在△ABC中,如果∠A-∠B=90°,那么△ABC是( ) (A)直角三角形(B)锐角三角形(C)钝角三角形(D)锐角三角形或钝角三角形【例题经典】直角三角形两锐角互余(大屏幕展示)理解直角三角形中边角之间的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,并会用解直角三角形的有关知识,在实际背景下逐步来解某些简单的实际问题例1.如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=______. 【分析】∠ABC与∠DFE分布在两个直角三角形中,若说明这两个直角三角形全等则问题便会迎刃而解.【解答】在Rt△ABC和Rt△DEF中,BC=EF,AC=DF,∴△ABC≌△DEF,∴∠ABC=∠DEF,∴∠ABC+∠DFE=90°,因此填90°.例2、如图2,将一副直角三角板叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC= 。特殊直角三角形的性质、勾股定理的应用例3.若直角三角形的三边长分别为2,4,x,则x的可能值有( ).(A)1个 (B)2个 (C)3个 (D)4个答案:B例4.如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=3,将BC向BA方向折过去,使点C落在BA上的C’点,折痕为BE,则C'E的长是 .答案: 勾股定理的逆定理的应用(大屏幕展示)例5.如图,正方形网格中,小格的顶点叫做格点,小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一实线上;②连结三个格点,使之构成直角三角形,小华在下面的正方形网格中作出了Rt△ABC.请你按照同样的要求,在右边的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形互不全等. 简析:此题的答案可以有很多种,关键是抓住有一直角这一特征,可以根据勾股定理的逆定理“有两边的平方和等于第三边的平方,则三角形为直角三角形”构造出直角三角形,答案如下图.练习:1.已知,如图所示,折叠长方形的一边AD,使点D落在BC边的点F处,如果AB=8cm,BC=10cm,(1)求EC的长;(2)在线段BC上还能找到点P使∠APE=90°吗,求出此时的BP长.2.如图,在梯形中,,,,于点,,,求BE的长度.3.如图,一块四边形土地,其中m,m,求这块土地的面积【作业设计】 集锦 必做:1选做:2
板书设计 【回顾与思考】 直角三角形
教学后记或反思(主要记录课堂设计理念,实际教学效果及改进设想等)
通过对近三年的中考题以及期末统考题进行了分析,发现主要考查的是直角三角形的应用问题。课时比较紧张,为了更好的让学生多得分,我在整整一节课中关注的基本都是直角三角形的应用问题,忽略了各层次学生的基本情况。一开始虽然有几道“基础”题,但都是与实际相结合的问题,学生上来就做这些题,中等层次以下的学生会找不到解决问题的钥匙,从而产生恐惧感。我结合了自己的教学风格以及任教班级学生的特点,对教案作深入的推敲、斟酌,调整了教学方式以及一部分题目。
图2
A
D
E
C
B
同课章节目录
