2021-2022学年北师大版九年级数学下册第3章圆 同步达标测试(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册第3章圆 同步达标测试(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 337.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 19:01:48 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《第3章圆》同步达标测试(附答案)
一.选择题(共14小题,满分42分)
1.下列语句中,正确的是( )
A.长度相等的弧是等弧
B.在同一平面上的三点确定一个圆
C.三角形的内心是三角形三边垂直平分线的交点
D.三角形的外心到三角形三个顶点的距离相等
2.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4 B.5 C.6 D.6
3.如图,一块直角三角板的30°角的顶点P落在⊙O上,两边分别交⊙O于A、B两点,若⊙O的直径为4,则弦AB长为( )
A.2 B.3 C. D.
4.如图,四边形ABCD内接于⊙O,E是BC延长线上一点,若∠BAD=100°,则∠DCE的大小是( )
A.115° B.105° C.100° D.95°
5.⊙O半径为5,圆心O的坐标为(0,0),点P的坐标为(3,4),则点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上
C.点P在⊙O外 D.点P在⊙O上或外
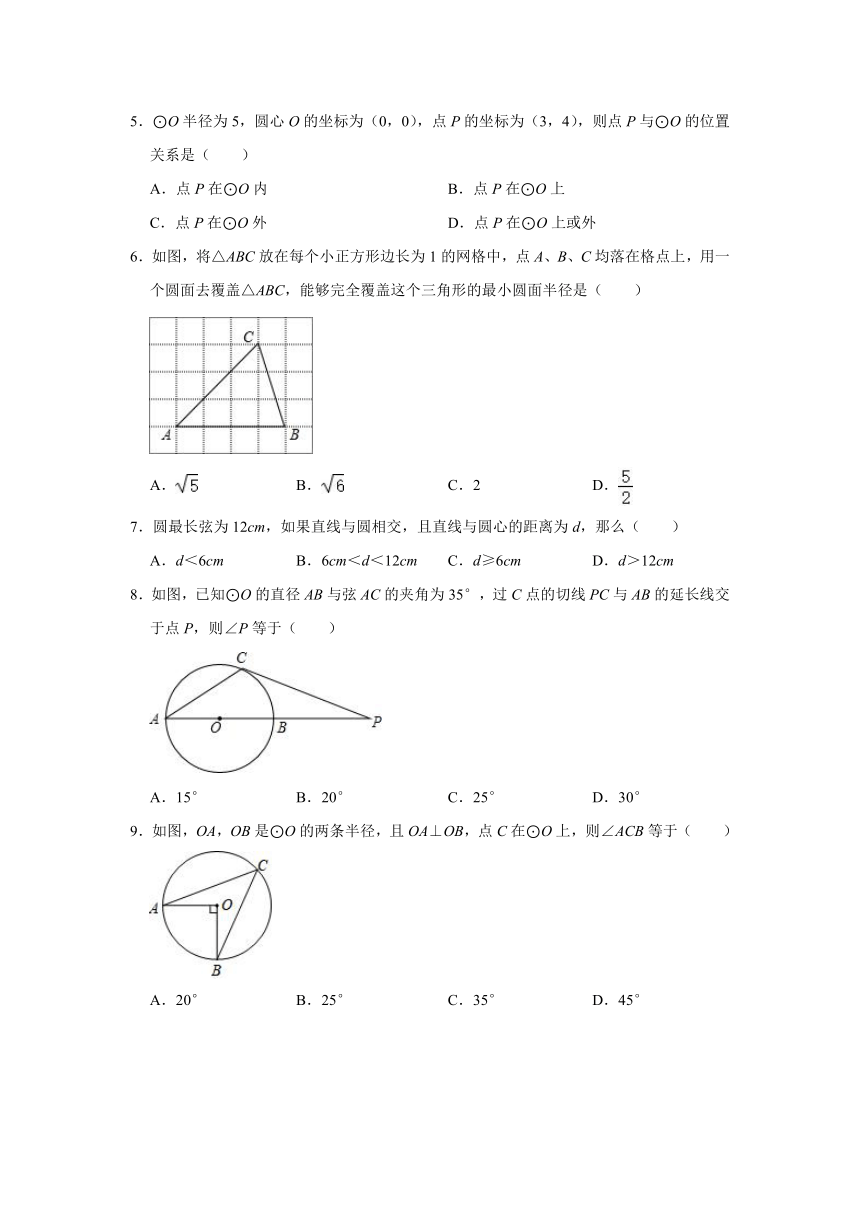
6.如图,将△ABC放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面半径是( )
A. B. C.2 D.
7.圆最长弦为12cm,如果直线与圆相交,且直线与圆心的距离为d,那么( )
A.d<6cm B.6cm<d<12cm C.d≥6cm D.d>12cm
8.如图,已知⊙O的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )
A.15° B.20° C.25° D.30°
9.如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB等于( )
A.20° B.25° C.35° D.45°
10.如图,已知平面直角坐标系内三点A(3,0)、B(5,0)、C(0,4),⊙P经过点A、B、C,则点P的坐标为( )
A.(6,8) B.(4,5) C.(4,) D.(4,)
11.如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP=QO,则的值为( )
A. B. C. D.
12.⊙O的半径是13,弦AB∥CD,AB=24,CD=10,则AB与CD的距离是( )
A.7 B.17 C.7或17 D.34
13.如图,⊙O中,CD是切线,切点是D,直线CO交⊙O于B、A,∠A=20°,则∠C的度数是( )
A.25° B.65° C.50° D.75°
14.如图,AB是⊙O的直径,点C为⊙O外一点,CA、CD是⊙O的切线,A、D为切点,连接BD、AD.若∠ACD=48°,则∠DBA的大小是( )
A.32° B.48° C.60° D.66°
二.填空题(共6小题,满分30分)
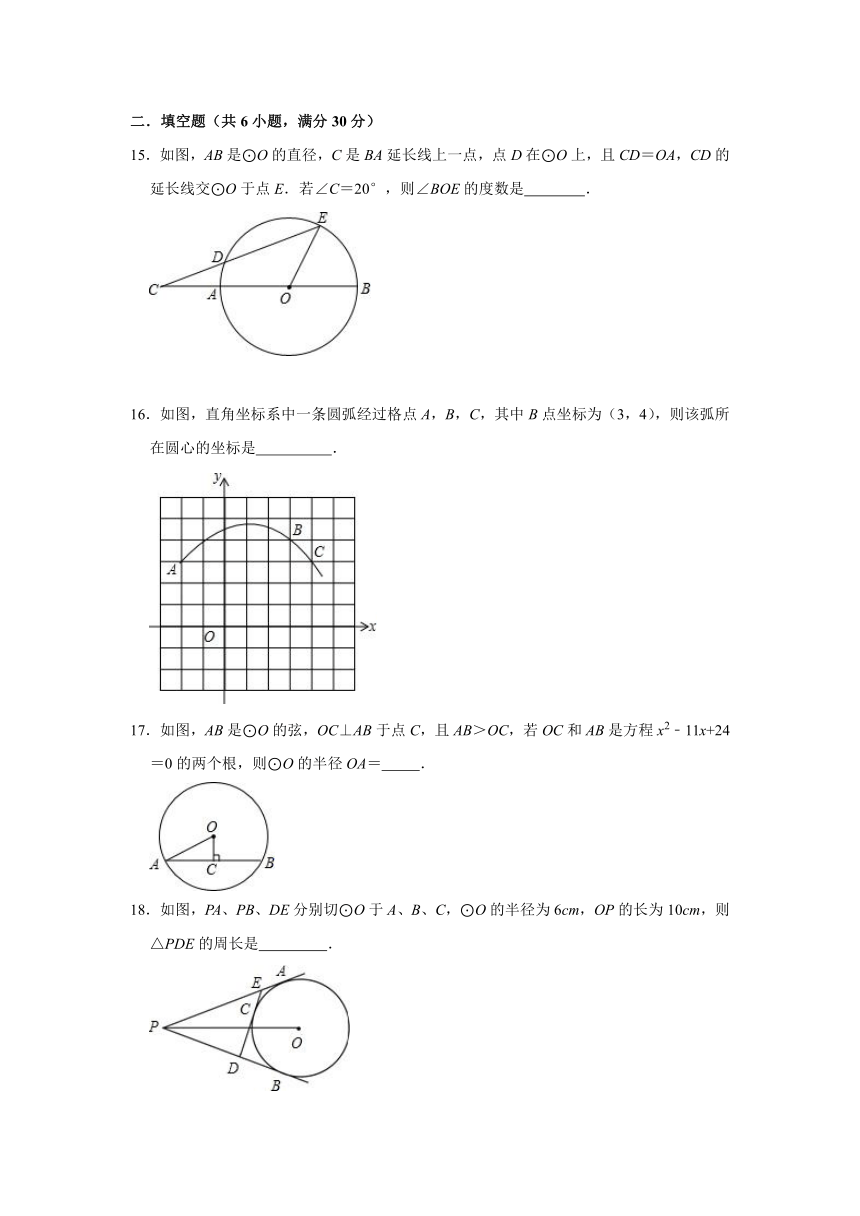
15.如图,AB是⊙O的直径,C是BA延长线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E.若∠C=20°,则∠BOE的度数是 .
16.如图,直角坐标系中一条圆弧经过格点A,B,C,其中B点坐标为(3,4),则该弧所在圆心的坐标是 .
17.如图,AB是⊙O的弦,OC⊥AB于点C,且AB>OC,若OC和AB是方程x2﹣11x+24=0的两个根,则⊙O的半径OA= .
18.如图,PA、PB、DE分别切⊙O于A、B、C,⊙O的半径为6cm,OP的长为10cm,则△PDE的周长是 .
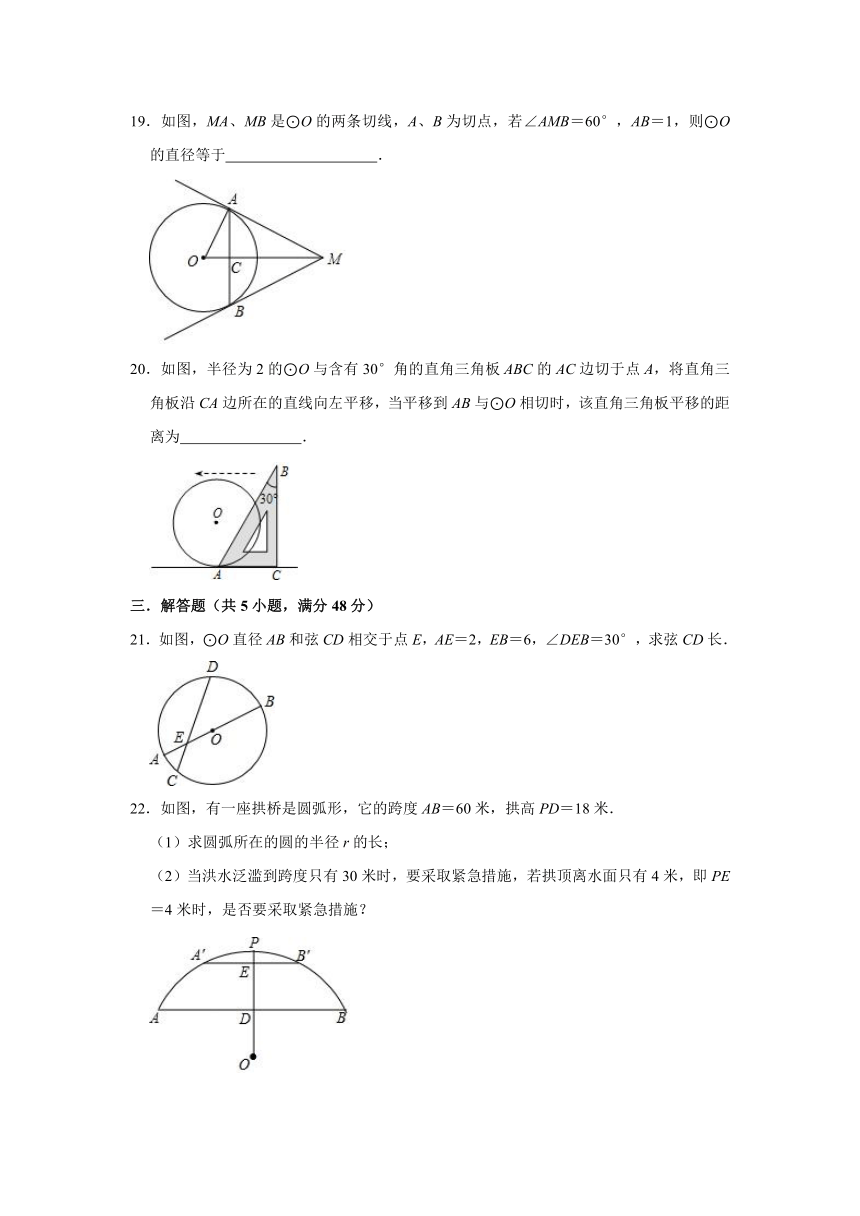
19.如图,MA、MB是⊙O的两条切线,A、B为切点,若∠AMB=60°,AB=1,则⊙O的直径等于 .
20.如图,半径为2的⊙O与含有30°角的直角三角板ABC的AC边切于点A,将直角三角板沿CA边所在的直线向左平移,当平移到AB与⊙O相切时,该直角三角板平移的距离为 .
三.解答题(共5小题,满分48分)
21.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
22.如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
23.如图,AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,OD⊥BC于E.
(1)求证:OD∥AC;
(2)若BC=8,DE=3,求⊙O的直径.
24. 如图,AB为⊙O的弦,C为劣弧AB的中点.
(1)若⊙O的半径为5,AB=8,求tan∠BAC;
(2)若∠DAC=∠BAC,且点D在⊙O的外部,判断AD与⊙O的位置关系,并说明理由.
25.如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD交圆的切线BE于点E
(1)判断直线PD是否为⊙O的切线,并说明理由;
(2)如果∠BED=60°,,求PA的长.
(3)在(2)的条件下,将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.
参考答案
一.选择题(共13小题,满分42分)
1.解:A、在同圆或等圆中,能完全重合的弧才是等弧,故错误;
B、不在同一直线上的三点确定一个圆,故错误;
C、三角形的内心到三边的距离相等,是三条角平分线的交点,故错误;
D、三角形的外心是外接圆的圆心,到三顶点的距离相等,故正确;
故选:D.
2.解:∵OC⊥AB,OC过圆心O点,
∴BC=AC=AB=×16=8,
在Rt△OCB中,由勾股定理得:OC===6,
故选:D.
3.解:连接AO并延长交⊙O于点D,连接BD,
∵∠P=30°,
∴∠D=∠P=30°.
∵AD是⊙O的直径,AD=4,
∴∠ABD=90°,
∴AB=AD=2.
故选:A.
4.解:∵∠BAD=100°,
∴∠BCD=180°﹣∠BAD=80°,
∴∠DCE=180°﹣∠BCD=100°.
故选:C.
5.解:∵点P的坐标为(3,4),
∴由勾股定理得,点P到圆心O的距离==5,
∴点P在⊙O上,故选B.
6.解:如图所示:点O为△ABC外接圆圆心,则AO为外接圆半径,
故能够完全覆盖这个三角形的最小圆面的半径是:.
故选:A.
7.解:由题意得
圆的直径为12,那么圆的半径为6.
则当直线与圆相交时,直线与圆心的距离d<6cm.
故选:A.
8.解:如图,连接OC.
∵OA=OC,
∴∠OAC=∠OCA=35°,
∴∠POC=∠OAC+∠OCA=70°,
∵PC是⊙O切线,
∴PC⊥OC,
∴∠PCO=90°,
∴∠P=90°﹣∠POC=20°,
故选:B.
9.解:∵OA⊥OB,
∴∠AOB=90°,
由圆周角定理得,∠ACB=∠AOB=45°,
故选:D.
10.解:∵⊙P经过点A、B、C,
∴点P在线段AB的垂直平分线上,
∴点P的横坐标为4,
设点P的坐标为(4,y),
作PE⊥OB于E,PF⊥OC于F,
由题意得,
=,
解得,y=,
故选:C.
11.解:如图,设⊙O的半径为r,QO=m,则QP=m,QC=r+m,
QA=r﹣m.
在⊙O中,根据相交弦定理,得QA QC=QP QD.
即(r﹣m)(r+m)=m QD,所以QD=.
连接DO,由勾股定理,得QD2=DO2+QO2,
即,
解得
所以,
故选:D.
12.解:如图,AE=AB=×24=12,
CF=CD=×10=5,
OE===5,
OF===12,
①当两弦在圆心同侧时,距离=OF﹣OE=12﹣5=7;
②当两弦在圆心异侧时,距离=OE+OF=12+5=17.
所以距离为7或17.
故选:C.
13.解:连接OD,
∵CD是⊙O的切线,
∴∠ODC=90°,
∠COD=2∠A=40°,
∴∠C=90°﹣40°=50°,
故选:C.
14.解:∵CA、CD是⊙O的切线,
∴CA=CD,
∵∠ACD=48°,
∴∠CAD=∠CDA=66°,
∵CA⊥AB,AB是直径,
∴∠ADB=∠CAB=90°,
∴∠DBA+∠DAB=90°,∠CAD+∠DAB=90°,
∴∠DBA=∠CAD=66°,
故选:D.
二.填空题(共6小题,满分30分)
15.解:连接OD,
∵CD=OA=OD,∠C=20°,
∴∠ODE=2∠C=40°,
∵OD=OE,
∴∠E=∠EDO=40°,
∴∠EOB=∠C+∠E=40°+20°=60°,
故答案为:60°.
16.解:如图所示,作弦AC和BC的垂直平分线,交点即为圆心.
如图所示,则圆心D(1,1).
故答案为:(1,1).
17.解:x2﹣11x+24=0
(x﹣3)(x﹣8)=0
x﹣3=0,x﹣8=0,
x1=3,x2=8,
∵AB>OC,
∴AB=8,OC=3,
∵OC⊥AB,
∴AC=AB=4,
由勾股定理得,OA==5,
故答案为:5.
18.解:连接OA.
∵PA、PB、DE分别切⊙O于A、B、C点,
∴BD=CD,CE=AE,PA=PB,OA⊥AP.
在直角三角形OAP中,根据勾股定理,得AP=8,
∴△PDE的周长为2AP=16.
故选答案为16cm.
19.解:连接OB,
∵MA、MB是⊙O的两条切线,A、B为切点,
∴AM=BM,∠OMA=∠AMB=30°,∠OAM=90°,
∵OA=OB,
∴OM是AB的垂直平分线,
∵AB=1,
∴AC=,
Rt△OAM中,∠AOM=60°,
∵∠ACO=90°,
∴sin60°=,
∴OA===,
∴⊙O的直径为:,
故答案为:.
20.解:根据题意画出平移后的图形,如图所示:
设平移后的△A′B′C′与圆O相切于点D,连接OD,OA,AD,
过O作OE⊥AD,可得E为AD的中点,
∵平移前圆O与AC相切于A点,
∴OA⊥A′C,即∠OAA′=90°,
∵平移前圆O与AC相切于A点,平移后圆O与A′B′相切于D点,
即A′D与A′A为圆O的两条切线,
∴A′D=A′A,又∠B′A′C′=60°,
∴△A′AD为等边三角形,
∴∠DAA′=60°,AD=AA′=A′D,
∴∠OAE=∠OAA′﹣∠DAA′=30°,
在Rt△AOE中,∠OAE=30°,AO=2,
∴AE=AO cos30°=,
∴AD=2AE=2,
∴AA′=2,
则该直角三角板平移的距离为2.
故答案为:2.
三.解答题(共5小题,满分48分)
21.解:过O作OF⊥CD,交CD于点F,连接OD,
∴F为CD的中点,即CF=DF,
∵AE=2,EB=6,
∴AB=AE+EB=2+6=8,
∴OA=4,
∴OE=OA﹣AE=4﹣2=2,
在Rt△OEF中,∠DEB=30°,
∴OF=OE=1,
在Rt△ODF中,OF=1,OD=4,
根据勾股定理得:DF==,
则CD=2DF=2.
22.解:(1)连接OA,
由题意得:AD=AB=30(米),OD=(r﹣18)米,
在Rt△ADO中,由勾股定理得:r2=302+(r﹣18)2,
解得,r=34(米);
(2)连接OA′,
∵OE=OP﹣PE=30米,
∴在Rt△A′EO中,由勾股定理得:A′E2=A′O2﹣OE2,即:A′E2=342﹣302,
解得:A′E=16(米).
∴A′B′=32(米).
∵A′B′=32>30,
∴不需要采取紧急措施.
23.(1)证明:∵AB是⊙O的直径,∴∠C=90°,
∵OD⊥BC,∴∠OEB=∠C=90°,
∴OD∥AC;
(2)解:令⊙O的半径为r,
根据垂径定理可得:BE=CE=BC=4,
由勾股定理得:r2=42+(r﹣3)2,
解得:r=,
所以⊙O的直径为.
24.解:(1)如图,∵AB为⊙O的弦,C为劣弧AB的中点,AB=8,
∴OC⊥AB于E,
∴,
又∵AO=5,
∴,
∴CE=OC﹣OE=2,
在Rt△AEC中,;
(2)AD与⊙O相切.理由如下:
∵OA=OC,
∴∠C=∠OAC,
∵由(1)知OC⊥AB,
∴∠C+∠BAC=90°.
又∵∠BAC=∠DAC,
∴∠OAC+∠DAC=90°,
∴AD与⊙O相切.
25.(1)解:直线PD为⊙O的切线
证明:如图1,连接OD,∵AB是圆O的直径,∴∠ADB=90°
∴∠ADO+∠BDO=90°,
又∵DO=BO,∴∠BDO=∠PBD
∵∠PDA=∠PBD,∴∠BDO=∠PDA
∴∠ADO+∠PDA=90°,即PD⊥OD
∵点D在⊙O上,∴直线PD为⊙O的切线.
(2)解:∵BE是⊙O的切线,∴∠EBA=90°
∵∠BED=60°,∴∠P=30°
∵PD为⊙O的切线,∴∠PDO=90°
在Rt△PDO中,∠P=30°,
∴,解得OD=1
∴
∴PA=PO﹣AO=2﹣1=1
(3)(方法一)证明:如图2,依题意得:∠ADF=∠PDA,∠PAD=∠DAF
∵∠PDA=∠PBD∠ADF=∠ABF
∴∠ADF=∠PDA=∠PBD=∠ABF
∵AB是圆O的直径∴∠ADB=90°
设∠PBD=x°,则∠DAF=∠PAD=90°+x°,∠DBF=2x°
∵四边形AFBD内接于⊙O,∴∠DAF+∠DBF=180°
即90°+x+2x=180°,解得x=30°
∴∠ADF=∠PDA=∠PBD=∠ABF=30°
∵BE、ED是⊙O的切线,∴DE=BE,∠EBA=90°
∴∠DBE=60°,∴△BDE是等边三角形.
∴BD=DE=BE
又∵∠FDB=∠ADB﹣∠ADF=90°﹣30°=60°∠DBF=2x°=60°
∴△BDF是等边三角形.∴BD=DF=BF
∴DE=BE=DF=BF,∴四边形DFBE为菱形
(方法二)证明:如图3,依题意得:∠ADF=∠PDA,∠APD=∠AFD,
∵∠PDA=∠PBD,∠ADF=∠ABF,∠PAD=∠DAF,
∴∠ADF=∠AFD=∠BPD=∠ABF
∴AD=AF,BF∥PD
∴DF⊥PB∵BE为切线∴BE⊥PB
∴DF∥BE
∴四边形DFBE为平行四边形
∵PE、BE为切线∴BE=DE
∴四边形DFBE为菱形
一.选择题(共14小题,满分42分)
1.下列语句中,正确的是( )
A.长度相等的弧是等弧
B.在同一平面上的三点确定一个圆
C.三角形的内心是三角形三边垂直平分线的交点
D.三角形的外心到三角形三个顶点的距离相等
2.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4 B.5 C.6 D.6
3.如图,一块直角三角板的30°角的顶点P落在⊙O上,两边分别交⊙O于A、B两点,若⊙O的直径为4,则弦AB长为( )
A.2 B.3 C. D.
4.如图,四边形ABCD内接于⊙O,E是BC延长线上一点,若∠BAD=100°,则∠DCE的大小是( )
A.115° B.105° C.100° D.95°
5.⊙O半径为5,圆心O的坐标为(0,0),点P的坐标为(3,4),则点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上
C.点P在⊙O外 D.点P在⊙O上或外
6.如图,将△ABC放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面半径是( )
A. B. C.2 D.
7.圆最长弦为12cm,如果直线与圆相交,且直线与圆心的距离为d,那么( )
A.d<6cm B.6cm<d<12cm C.d≥6cm D.d>12cm
8.如图,已知⊙O的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )
A.15° B.20° C.25° D.30°
9.如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB等于( )
A.20° B.25° C.35° D.45°
10.如图,已知平面直角坐标系内三点A(3,0)、B(5,0)、C(0,4),⊙P经过点A、B、C,则点P的坐标为( )
A.(6,8) B.(4,5) C.(4,) D.(4,)
11.如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP=QO,则的值为( )
A. B. C. D.
12.⊙O的半径是13,弦AB∥CD,AB=24,CD=10,则AB与CD的距离是( )
A.7 B.17 C.7或17 D.34
13.如图,⊙O中,CD是切线,切点是D,直线CO交⊙O于B、A,∠A=20°,则∠C的度数是( )
A.25° B.65° C.50° D.75°
14.如图,AB是⊙O的直径,点C为⊙O外一点,CA、CD是⊙O的切线,A、D为切点,连接BD、AD.若∠ACD=48°,则∠DBA的大小是( )
A.32° B.48° C.60° D.66°
二.填空题(共6小题,满分30分)
15.如图,AB是⊙O的直径,C是BA延长线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E.若∠C=20°,则∠BOE的度数是 .
16.如图,直角坐标系中一条圆弧经过格点A,B,C,其中B点坐标为(3,4),则该弧所在圆心的坐标是 .
17.如图,AB是⊙O的弦,OC⊥AB于点C,且AB>OC,若OC和AB是方程x2﹣11x+24=0的两个根,则⊙O的半径OA= .
18.如图,PA、PB、DE分别切⊙O于A、B、C,⊙O的半径为6cm,OP的长为10cm,则△PDE的周长是 .
19.如图,MA、MB是⊙O的两条切线,A、B为切点,若∠AMB=60°,AB=1,则⊙O的直径等于 .
20.如图,半径为2的⊙O与含有30°角的直角三角板ABC的AC边切于点A,将直角三角板沿CA边所在的直线向左平移,当平移到AB与⊙O相切时,该直角三角板平移的距离为 .
三.解答题(共5小题,满分48分)
21.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
22.如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
23.如图,AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,OD⊥BC于E.
(1)求证:OD∥AC;
(2)若BC=8,DE=3,求⊙O的直径.
24. 如图,AB为⊙O的弦,C为劣弧AB的中点.
(1)若⊙O的半径为5,AB=8,求tan∠BAC;
(2)若∠DAC=∠BAC,且点D在⊙O的外部,判断AD与⊙O的位置关系,并说明理由.
25.如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD交圆的切线BE于点E
(1)判断直线PD是否为⊙O的切线,并说明理由;
(2)如果∠BED=60°,,求PA的长.
(3)在(2)的条件下,将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.
参考答案
一.选择题(共13小题,满分42分)
1.解:A、在同圆或等圆中,能完全重合的弧才是等弧,故错误;
B、不在同一直线上的三点确定一个圆,故错误;
C、三角形的内心到三边的距离相等,是三条角平分线的交点,故错误;
D、三角形的外心是外接圆的圆心,到三顶点的距离相等,故正确;
故选:D.
2.解:∵OC⊥AB,OC过圆心O点,
∴BC=AC=AB=×16=8,
在Rt△OCB中,由勾股定理得:OC===6,
故选:D.
3.解:连接AO并延长交⊙O于点D,连接BD,
∵∠P=30°,
∴∠D=∠P=30°.
∵AD是⊙O的直径,AD=4,
∴∠ABD=90°,
∴AB=AD=2.
故选:A.
4.解:∵∠BAD=100°,
∴∠BCD=180°﹣∠BAD=80°,
∴∠DCE=180°﹣∠BCD=100°.
故选:C.
5.解:∵点P的坐标为(3,4),
∴由勾股定理得,点P到圆心O的距离==5,
∴点P在⊙O上,故选B.
6.解:如图所示:点O为△ABC外接圆圆心,则AO为外接圆半径,
故能够完全覆盖这个三角形的最小圆面的半径是:.
故选:A.
7.解:由题意得
圆的直径为12,那么圆的半径为6.
则当直线与圆相交时,直线与圆心的距离d<6cm.
故选:A.
8.解:如图,连接OC.
∵OA=OC,
∴∠OAC=∠OCA=35°,
∴∠POC=∠OAC+∠OCA=70°,
∵PC是⊙O切线,
∴PC⊥OC,
∴∠PCO=90°,
∴∠P=90°﹣∠POC=20°,
故选:B.
9.解:∵OA⊥OB,
∴∠AOB=90°,
由圆周角定理得,∠ACB=∠AOB=45°,
故选:D.
10.解:∵⊙P经过点A、B、C,
∴点P在线段AB的垂直平分线上,
∴点P的横坐标为4,
设点P的坐标为(4,y),
作PE⊥OB于E,PF⊥OC于F,
由题意得,
=,
解得,y=,
故选:C.
11.解:如图,设⊙O的半径为r,QO=m,则QP=m,QC=r+m,
QA=r﹣m.
在⊙O中,根据相交弦定理,得QA QC=QP QD.
即(r﹣m)(r+m)=m QD,所以QD=.
连接DO,由勾股定理,得QD2=DO2+QO2,
即,
解得
所以,
故选:D.
12.解:如图,AE=AB=×24=12,
CF=CD=×10=5,
OE===5,
OF===12,
①当两弦在圆心同侧时,距离=OF﹣OE=12﹣5=7;
②当两弦在圆心异侧时,距离=OE+OF=12+5=17.
所以距离为7或17.
故选:C.
13.解:连接OD,
∵CD是⊙O的切线,
∴∠ODC=90°,
∠COD=2∠A=40°,
∴∠C=90°﹣40°=50°,
故选:C.
14.解:∵CA、CD是⊙O的切线,
∴CA=CD,
∵∠ACD=48°,
∴∠CAD=∠CDA=66°,
∵CA⊥AB,AB是直径,
∴∠ADB=∠CAB=90°,
∴∠DBA+∠DAB=90°,∠CAD+∠DAB=90°,
∴∠DBA=∠CAD=66°,
故选:D.
二.填空题(共6小题,满分30分)
15.解:连接OD,
∵CD=OA=OD,∠C=20°,
∴∠ODE=2∠C=40°,
∵OD=OE,
∴∠E=∠EDO=40°,
∴∠EOB=∠C+∠E=40°+20°=60°,
故答案为:60°.
16.解:如图所示,作弦AC和BC的垂直平分线,交点即为圆心.
如图所示,则圆心D(1,1).
故答案为:(1,1).
17.解:x2﹣11x+24=0
(x﹣3)(x﹣8)=0
x﹣3=0,x﹣8=0,
x1=3,x2=8,
∵AB>OC,
∴AB=8,OC=3,
∵OC⊥AB,
∴AC=AB=4,
由勾股定理得,OA==5,
故答案为:5.
18.解:连接OA.
∵PA、PB、DE分别切⊙O于A、B、C点,
∴BD=CD,CE=AE,PA=PB,OA⊥AP.
在直角三角形OAP中,根据勾股定理,得AP=8,
∴△PDE的周长为2AP=16.
故选答案为16cm.
19.解:连接OB,
∵MA、MB是⊙O的两条切线,A、B为切点,
∴AM=BM,∠OMA=∠AMB=30°,∠OAM=90°,
∵OA=OB,
∴OM是AB的垂直平分线,
∵AB=1,
∴AC=,
Rt△OAM中,∠AOM=60°,
∵∠ACO=90°,
∴sin60°=,
∴OA===,
∴⊙O的直径为:,
故答案为:.
20.解:根据题意画出平移后的图形,如图所示:
设平移后的△A′B′C′与圆O相切于点D,连接OD,OA,AD,
过O作OE⊥AD,可得E为AD的中点,
∵平移前圆O与AC相切于A点,
∴OA⊥A′C,即∠OAA′=90°,
∵平移前圆O与AC相切于A点,平移后圆O与A′B′相切于D点,
即A′D与A′A为圆O的两条切线,
∴A′D=A′A,又∠B′A′C′=60°,
∴△A′AD为等边三角形,
∴∠DAA′=60°,AD=AA′=A′D,
∴∠OAE=∠OAA′﹣∠DAA′=30°,
在Rt△AOE中,∠OAE=30°,AO=2,
∴AE=AO cos30°=,
∴AD=2AE=2,
∴AA′=2,
则该直角三角板平移的距离为2.
故答案为:2.
三.解答题(共5小题,满分48分)
21.解:过O作OF⊥CD,交CD于点F,连接OD,
∴F为CD的中点,即CF=DF,
∵AE=2,EB=6,
∴AB=AE+EB=2+6=8,
∴OA=4,
∴OE=OA﹣AE=4﹣2=2,
在Rt△OEF中,∠DEB=30°,
∴OF=OE=1,
在Rt△ODF中,OF=1,OD=4,
根据勾股定理得:DF==,
则CD=2DF=2.
22.解:(1)连接OA,
由题意得:AD=AB=30(米),OD=(r﹣18)米,
在Rt△ADO中,由勾股定理得:r2=302+(r﹣18)2,
解得,r=34(米);
(2)连接OA′,
∵OE=OP﹣PE=30米,
∴在Rt△A′EO中,由勾股定理得:A′E2=A′O2﹣OE2,即:A′E2=342﹣302,
解得:A′E=16(米).
∴A′B′=32(米).
∵A′B′=32>30,
∴不需要采取紧急措施.
23.(1)证明:∵AB是⊙O的直径,∴∠C=90°,
∵OD⊥BC,∴∠OEB=∠C=90°,
∴OD∥AC;
(2)解:令⊙O的半径为r,
根据垂径定理可得:BE=CE=BC=4,
由勾股定理得:r2=42+(r﹣3)2,
解得:r=,
所以⊙O的直径为.
24.解:(1)如图,∵AB为⊙O的弦,C为劣弧AB的中点,AB=8,
∴OC⊥AB于E,
∴,
又∵AO=5,
∴,
∴CE=OC﹣OE=2,
在Rt△AEC中,;
(2)AD与⊙O相切.理由如下:
∵OA=OC,
∴∠C=∠OAC,
∵由(1)知OC⊥AB,
∴∠C+∠BAC=90°.
又∵∠BAC=∠DAC,
∴∠OAC+∠DAC=90°,
∴AD与⊙O相切.
25.(1)解:直线PD为⊙O的切线
证明:如图1,连接OD,∵AB是圆O的直径,∴∠ADB=90°
∴∠ADO+∠BDO=90°,
又∵DO=BO,∴∠BDO=∠PBD
∵∠PDA=∠PBD,∴∠BDO=∠PDA
∴∠ADO+∠PDA=90°,即PD⊥OD
∵点D在⊙O上,∴直线PD为⊙O的切线.
(2)解:∵BE是⊙O的切线,∴∠EBA=90°
∵∠BED=60°,∴∠P=30°
∵PD为⊙O的切线,∴∠PDO=90°
在Rt△PDO中,∠P=30°,
∴,解得OD=1
∴
∴PA=PO﹣AO=2﹣1=1
(3)(方法一)证明:如图2,依题意得:∠ADF=∠PDA,∠PAD=∠DAF
∵∠PDA=∠PBD∠ADF=∠ABF
∴∠ADF=∠PDA=∠PBD=∠ABF
∵AB是圆O的直径∴∠ADB=90°
设∠PBD=x°,则∠DAF=∠PAD=90°+x°,∠DBF=2x°
∵四边形AFBD内接于⊙O,∴∠DAF+∠DBF=180°
即90°+x+2x=180°,解得x=30°
∴∠ADF=∠PDA=∠PBD=∠ABF=30°
∵BE、ED是⊙O的切线,∴DE=BE,∠EBA=90°
∴∠DBE=60°,∴△BDE是等边三角形.
∴BD=DE=BE
又∵∠FDB=∠ADB﹣∠ADF=90°﹣30°=60°∠DBF=2x°=60°
∴△BDF是等边三角形.∴BD=DF=BF
∴DE=BE=DF=BF,∴四边形DFBE为菱形
(方法二)证明:如图3,依题意得:∠ADF=∠PDA,∠APD=∠AFD,
∵∠PDA=∠PBD,∠ADF=∠ABF,∠PAD=∠DAF,
∴∠ADF=∠AFD=∠BPD=∠ABF
∴AD=AF,BF∥PD
∴DF⊥PB∵BE为切线∴BE⊥PB
∴DF∥BE
∴四边形DFBE为平行四边形
∵PE、BE为切线∴BE=DE
∴四边形DFBE为菱形
