2021-2022学年苏科版七年级数学下册第7章 平面图形的认识(二)自我综合评价 (word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册第7章 平面图形的认识(二)自我综合评价 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 205.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 17:58:37 | ||
图片预览


文档简介
第7章 平面图形的认识(二)
一、选择题(本大题共6小题,每小题4分,共24分;在每个小题列出的四个选项中,只有一项符合题意)
1.下列各组图形可以通过平移互相得到的是 ( )
2.如图,下列结论中错误的是 ( )
A.∠1与∠C是同位角
B.∠2与∠C是内错角
C.∠3与∠B是同旁内角
D.∠3与∠C是同旁内角
3.如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是 ( )
A.AC是△ABC的高
B.DE是△BCD的高
C.DE是△ABE的高
D.AD是△ACD的高
4.如图,a∥b,∠ABD的平分线交直线a于点C,CE⊥直线c于点E,∠1=24°,则∠2的大小为 ( )
A.114° B.142° C.147° D.156°
5. 若一个多边形的每一个外角都是24°,则此多边形的内角和为 ( )
A.2160° B.2340° C.2700° D.2880°
6.如图为长方形ABCD,一条直线将该长方形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( )
A.360° B.540° C.630° D.720°
二、填空题(本大题共6小题,每小题5分,共30分)
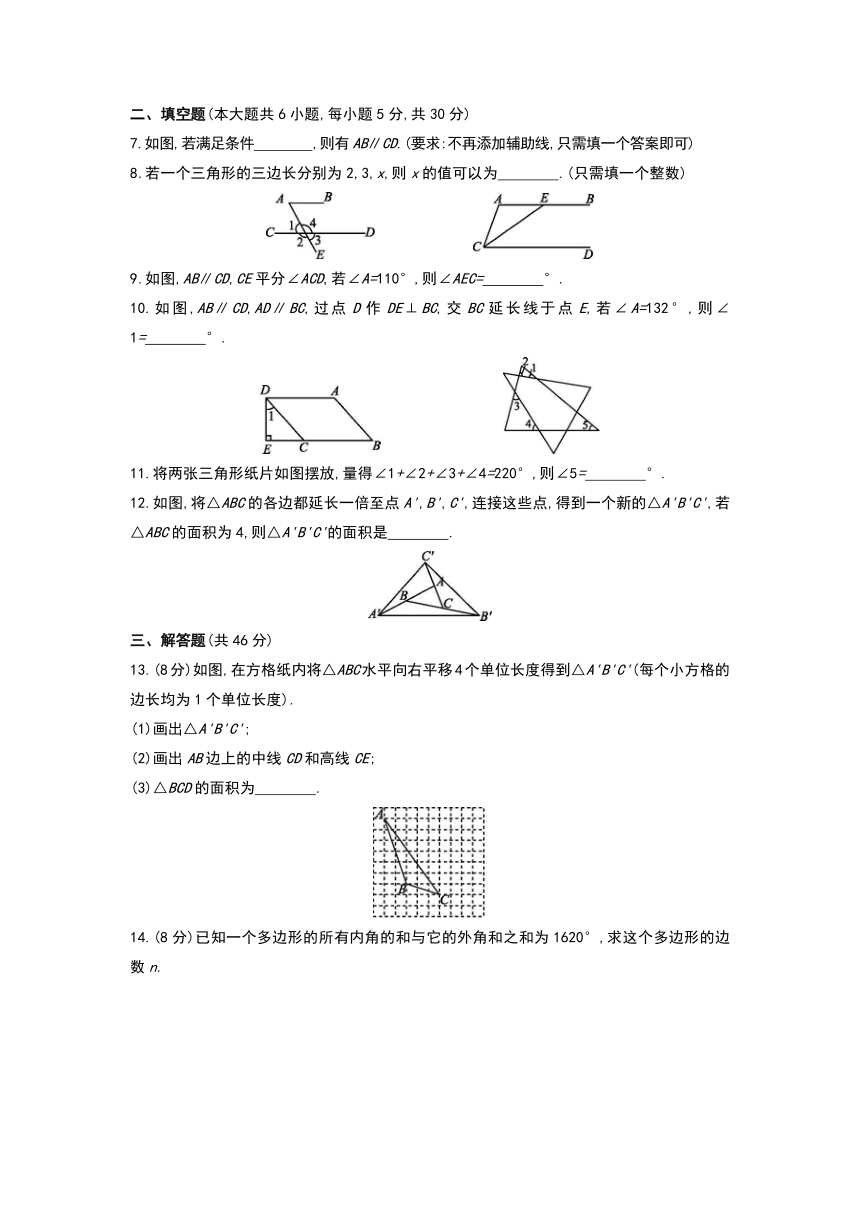
7.如图,若满足条件 ,则有AB∥CD.(要求:不再添加辅助线,只需填一个答案即可)
8.若一个三角形的三边长分别为2,3,x,则x的值可以为 .(只需填一个整数)
9.如图,AB∥CD,CE平分∠ACD,若∠A=110°,则∠AEC= °.
10.如图,AB∥CD,AD∥BC,过点D作DE⊥BC,交BC延长线于点E,若∠A=132°,则∠1= °.
11.将两张三角形纸片如图摆放,量得∠1+∠2+∠3+∠4=220°,则∠5= °.
12.如图,将△ABC的各边都延长一倍至点A',B',C',连接这些点,得到一个新的△A'B'C',若△ABC的面积为4,则△A'B'C'的面积是 .
三、解答题(共46分)
13.(8分)如图,在方格纸内将△ABC水平向右平移4个单位长度得到△A'B'C'(每个小方格的边长均为1个单位长度).
(1)画出△A'B'C';
(2)画出AB边上的中线CD和高线CE;
(3)△BCD的面积为 .
14.(8分)已知一个多边形的所有内角的和与它的外角和之和为1620°,求这个多边形的边数n.
15.(8分)如图,在四边形ABCD中,∠BAD=100°,∠BCD=70°,点M,N分别在AB,BC上,将△BMN沿MN翻折,得到△FMN.若MF∥AD,FN∥DC,求∠B的度数.
16.(10分)如图,点A,E,B在同一直线上,已知∠1+∠2=180°,∠B=∠3,∠BAC与∠DCA相等吗 为什么
17.(12分)如图,直线MN与直线PQ相交于点O,∠POM=60°,点A在射线OP上运动,点B在射线OM上运动.
(1)如图①,若∠BAO=70°,且AE,BE分别平分∠BAO和∠ABO,求∠AEB的度数.
(2)如图②,已知AD,BC分别是∠BAP和∠ABM的平分线,DE,CE分别是∠ADC和∠BCD的平分线,点A,B在运动的过程中(AB与CD不平行),∠CED的大小是否会发生变化 若发生变化,请说明理由;若不发生变化,请求出其值.
自我综合评价
1.C 观察图形可知C选项中的图案通过平移后可以互相得到.
2.B 3.C
4.C 由∠1=24°,CE⊥直线c于点E,得∠EAC=90°-∠1=90°-24°=66°,而a∥b,则∠EAC=∠ABD=66°.由∠ABD的平分线交直线a于点C,可得∠CBD=∠ABD=×66°=33°,所以∠2=180°-∠CBD=180°-33°=147°.
5. B
6.C 一条直线将该长方形ABCD分割成两个多边形,每一个多边形的内角和都是180°的整数倍,都能被180°整除,分析四个答案,只有630°不能被180°整除,所以a+b不可能是630°.故选C.
7.答案不唯一,如∠A=∠3
8.答案不唯一,如2或3或4,只要填其中一个即可
根据三角形的三边关系得3-2因为x为整数,所以x可以为2或3或4.
9.35 由AB∥CD,得∠AEC=∠DCE,∠ACD=180°-∠A=70°,
而CE平分∠ACD,所以∠ACE=∠DCE=35°,所以∠AEC=∠DCE=35°.
10.42 由AD∥BC,得∠B=180°-∠A=48°.
因为AB∥CD,则∠DCE=∠B=48°.
因为DE⊥BC,所以∠1=180°-90°-48°=42°.
11.40 如图.
因为∠1+∠2+∠6=180°,∠3+∠4+∠7=180°,
所以∠1+∠2+∠3+∠4+∠6+∠7=360°.
又因为∠1+∠2+∠3+∠4=220°,
所以∠6+∠7=140°,
所以∠5=180°-∠6-∠7=40°.
12.28 如图,连接C'B.
因为AA'=2AB,
所以S△A'C'A=2S△BAC'.
因为AC'=AC,
所以S△ABC'=S△ABC=4,
所以S△A'C'A=8.同理S△A'BB'=S△CC'B'=8,
所以△A'B'C'的面积是8+8+8+4=28.
故答案为28.
13.解:(1)如图所示,△A'B'C'即为所求.
(2)如图所示,CD,CE即为所求.
(3)4
14.解:根据题意,得(n-2)·180°+360°=1620°,
解得n=9.故这个多边形的边数n为9.
15.解:因为MF∥AD,FN∥DC,
所以∠BMF=∠A=100°,
∠BNF=∠C=70°(两直线平行,同位角相等).
因为△BMN沿MN翻折,得到△FMN,
所以∠BMN=∠BMF=50°,∠BNM=∠BNF=35°.
在△BMN中,∠B=180°-(∠BMN+∠BNM)=180°-(50°+35°)=180°-85°=95°.
16.解:∠BAC=∠DCA.理由:
因为∠CFE=∠2,∠2+∠1=180°,所以∠CFE+∠1=180°,
所以DE∥BC,所以∠AED=∠B.
因为∠B=∠3,所以∠3=∠AED,
所以AB∥CD,所以∠BAC=∠DCA.
17.解:(1)由BE平分∠ABO,AE平分∠BAO,
得∠EBA+∠EAB=(∠ABO+∠BAO)=(180°-∠AOB)=60°,
则∠AEB=180°-(∠EBA+∠EAB)=120°.
(2)∠CED的大小不变.
如图,延长AD,BC交于点F.
由∠AOB=60°,得∠OAB+∠OBA=120°,
则∠BAP+∠MBA=(180°-∠OAB)+(180°-∠OBA)=240°.
因为AD,BC分别是∠BAP和∠ABM的平分线,
所以∠BAD=∠BAP,∠ABC=∠ABM,
则∠BAD+∠ABC=(∠BAP+∠ABM)=120°,
所以∠F=60°,
则有∠FDC+∠FCD=120°,
所以∠CDA+∠DCB=(180°-∠FDC)+(180°-∠FCD)=240°.
因为DE,CE分别是∠ADC和∠BCD的平分线,
所以∠CDE+∠DCE=120°,
所以∠CED=180°-(∠CDE+∠DCE)=60°.
一、选择题(本大题共6小题,每小题4分,共24分;在每个小题列出的四个选项中,只有一项符合题意)
1.下列各组图形可以通过平移互相得到的是 ( )
2.如图,下列结论中错误的是 ( )
A.∠1与∠C是同位角
B.∠2与∠C是内错角
C.∠3与∠B是同旁内角
D.∠3与∠C是同旁内角
3.如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是 ( )
A.AC是△ABC的高
B.DE是△BCD的高
C.DE是△ABE的高
D.AD是△ACD的高
4.如图,a∥b,∠ABD的平分线交直线a于点C,CE⊥直线c于点E,∠1=24°,则∠2的大小为 ( )
A.114° B.142° C.147° D.156°
5. 若一个多边形的每一个外角都是24°,则此多边形的内角和为 ( )
A.2160° B.2340° C.2700° D.2880°
6.如图为长方形ABCD,一条直线将该长方形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( )
A.360° B.540° C.630° D.720°
二、填空题(本大题共6小题,每小题5分,共30分)
7.如图,若满足条件 ,则有AB∥CD.(要求:不再添加辅助线,只需填一个答案即可)
8.若一个三角形的三边长分别为2,3,x,则x的值可以为 .(只需填一个整数)
9.如图,AB∥CD,CE平分∠ACD,若∠A=110°,则∠AEC= °.
10.如图,AB∥CD,AD∥BC,过点D作DE⊥BC,交BC延长线于点E,若∠A=132°,则∠1= °.
11.将两张三角形纸片如图摆放,量得∠1+∠2+∠3+∠4=220°,则∠5= °.
12.如图,将△ABC的各边都延长一倍至点A',B',C',连接这些点,得到一个新的△A'B'C',若△ABC的面积为4,则△A'B'C'的面积是 .
三、解答题(共46分)
13.(8分)如图,在方格纸内将△ABC水平向右平移4个单位长度得到△A'B'C'(每个小方格的边长均为1个单位长度).
(1)画出△A'B'C';
(2)画出AB边上的中线CD和高线CE;
(3)△BCD的面积为 .
14.(8分)已知一个多边形的所有内角的和与它的外角和之和为1620°,求这个多边形的边数n.
15.(8分)如图,在四边形ABCD中,∠BAD=100°,∠BCD=70°,点M,N分别在AB,BC上,将△BMN沿MN翻折,得到△FMN.若MF∥AD,FN∥DC,求∠B的度数.
16.(10分)如图,点A,E,B在同一直线上,已知∠1+∠2=180°,∠B=∠3,∠BAC与∠DCA相等吗 为什么
17.(12分)如图,直线MN与直线PQ相交于点O,∠POM=60°,点A在射线OP上运动,点B在射线OM上运动.
(1)如图①,若∠BAO=70°,且AE,BE分别平分∠BAO和∠ABO,求∠AEB的度数.
(2)如图②,已知AD,BC分别是∠BAP和∠ABM的平分线,DE,CE分别是∠ADC和∠BCD的平分线,点A,B在运动的过程中(AB与CD不平行),∠CED的大小是否会发生变化 若发生变化,请说明理由;若不发生变化,请求出其值.
自我综合评价
1.C 观察图形可知C选项中的图案通过平移后可以互相得到.
2.B 3.C
4.C 由∠1=24°,CE⊥直线c于点E,得∠EAC=90°-∠1=90°-24°=66°,而a∥b,则∠EAC=∠ABD=66°.由∠ABD的平分线交直线a于点C,可得∠CBD=∠ABD=×66°=33°,所以∠2=180°-∠CBD=180°-33°=147°.
5. B
6.C 一条直线将该长方形ABCD分割成两个多边形,每一个多边形的内角和都是180°的整数倍,都能被180°整除,分析四个答案,只有630°不能被180°整除,所以a+b不可能是630°.故选C.
7.答案不唯一,如∠A=∠3
8.答案不唯一,如2或3或4,只要填其中一个即可
根据三角形的三边关系得3-2
9.35 由AB∥CD,得∠AEC=∠DCE,∠ACD=180°-∠A=70°,
而CE平分∠ACD,所以∠ACE=∠DCE=35°,所以∠AEC=∠DCE=35°.
10.42 由AD∥BC,得∠B=180°-∠A=48°.
因为AB∥CD,则∠DCE=∠B=48°.
因为DE⊥BC,所以∠1=180°-90°-48°=42°.
11.40 如图.
因为∠1+∠2+∠6=180°,∠3+∠4+∠7=180°,
所以∠1+∠2+∠3+∠4+∠6+∠7=360°.
又因为∠1+∠2+∠3+∠4=220°,
所以∠6+∠7=140°,
所以∠5=180°-∠6-∠7=40°.
12.28 如图,连接C'B.
因为AA'=2AB,
所以S△A'C'A=2S△BAC'.
因为AC'=AC,
所以S△ABC'=S△ABC=4,
所以S△A'C'A=8.同理S△A'BB'=S△CC'B'=8,
所以△A'B'C'的面积是8+8+8+4=28.
故答案为28.
13.解:(1)如图所示,△A'B'C'即为所求.
(2)如图所示,CD,CE即为所求.
(3)4
14.解:根据题意,得(n-2)·180°+360°=1620°,
解得n=9.故这个多边形的边数n为9.
15.解:因为MF∥AD,FN∥DC,
所以∠BMF=∠A=100°,
∠BNF=∠C=70°(两直线平行,同位角相等).
因为△BMN沿MN翻折,得到△FMN,
所以∠BMN=∠BMF=50°,∠BNM=∠BNF=35°.
在△BMN中,∠B=180°-(∠BMN+∠BNM)=180°-(50°+35°)=180°-85°=95°.
16.解:∠BAC=∠DCA.理由:
因为∠CFE=∠2,∠2+∠1=180°,所以∠CFE+∠1=180°,
所以DE∥BC,所以∠AED=∠B.
因为∠B=∠3,所以∠3=∠AED,
所以AB∥CD,所以∠BAC=∠DCA.
17.解:(1)由BE平分∠ABO,AE平分∠BAO,
得∠EBA+∠EAB=(∠ABO+∠BAO)=(180°-∠AOB)=60°,
则∠AEB=180°-(∠EBA+∠EAB)=120°.
(2)∠CED的大小不变.
如图,延长AD,BC交于点F.
由∠AOB=60°,得∠OAB+∠OBA=120°,
则∠BAP+∠MBA=(180°-∠OAB)+(180°-∠OBA)=240°.
因为AD,BC分别是∠BAP和∠ABM的平分线,
所以∠BAD=∠BAP,∠ABC=∠ABM,
则∠BAD+∠ABC=(∠BAP+∠ABM)=120°,
所以∠F=60°,
则有∠FDC+∠FCD=120°,
所以∠CDA+∠DCB=(180°-∠FDC)+(180°-∠FCD)=240°.
因为DE,CE分别是∠ADC和∠BCD的平分线,
所以∠CDE+∠DCE=120°,
所以∠CED=180°-(∠CDE+∠DCE)=60°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
