2021-2022学年华东师大版八年级数学上册 第14章勾股定理 同步练习题(word版含解析)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上册 第14章勾股定理 同步练习题(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 319.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 19:02:19 | ||
图片预览

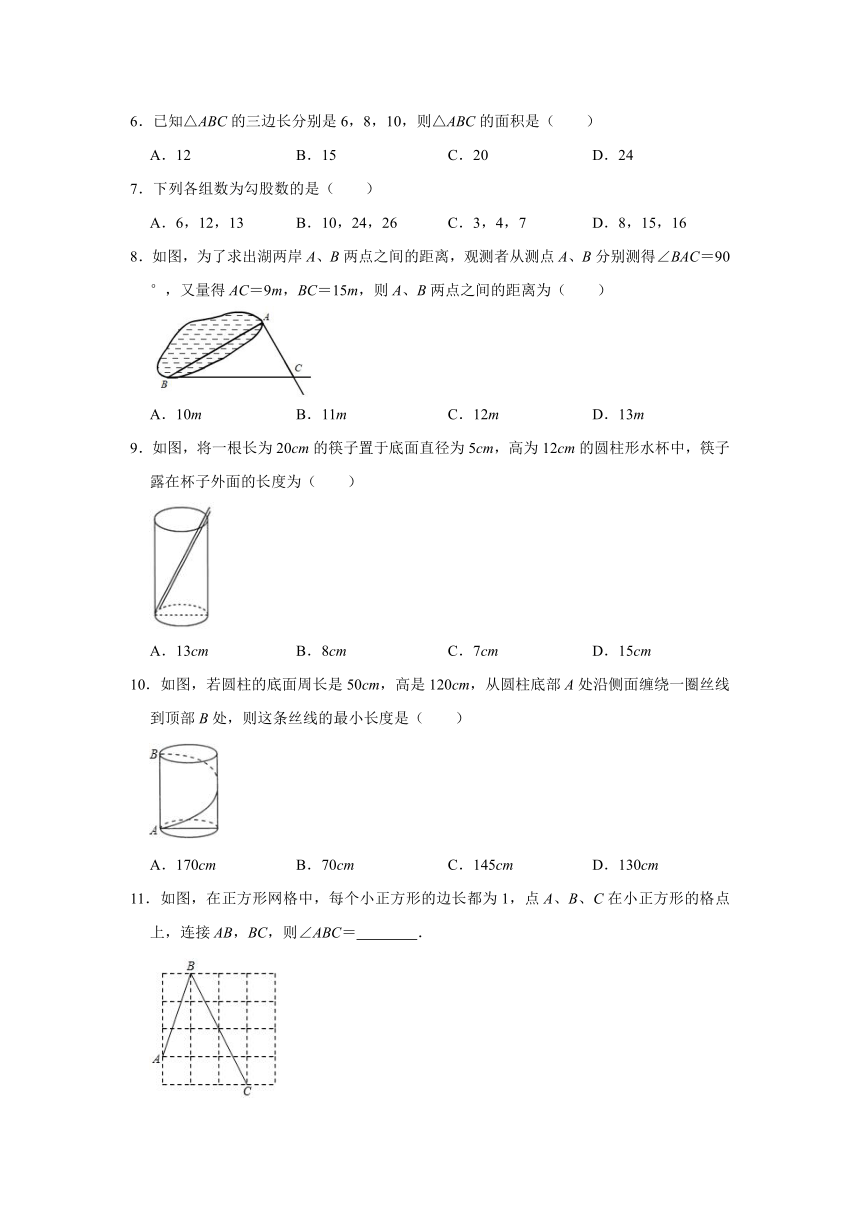


文档简介
2021-2022学年华师大版八年级数学上册《第14章勾股定理》同步练习题(附答案)
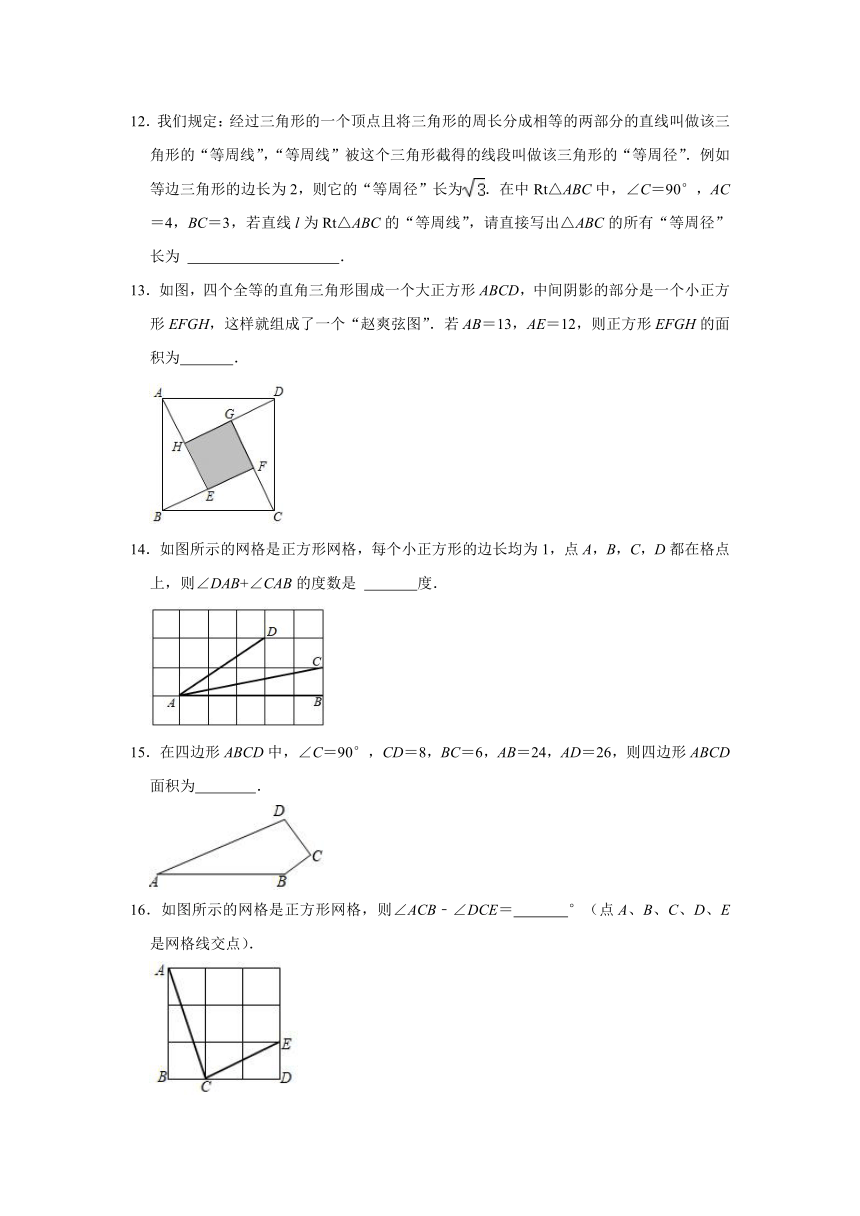
1.如图,∠AOB=60°,C是BO延长线上一点,OC=12cm,动点P从点C出发沿CB以2cm/s的速度移动,动点Q从点O出发沿OA以1cm/s的速度移动,如果点P,Q同时出发,用t表示移动的时间,若△POQ是等腰三角形,此时t的值是( )
A.6或12 B.4或12 C.4或6 D.6或8
2.在直角三角形中,若两条边的长分别是1cm、2cm,则第三边的长为( )
A.3cm B.cm C.2cm或cm D.cm或cm
3.如图所示的是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形
拼接而成,其中AE=10,BE=24,则EF2的值是( )
A.169 B.196 C.392 D.588
4.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图以直角三角形的各边为边分别向同侧作正方形,若知道图中阴影部分的面积之和,则一定能求出( )
A.正方形ABED的面积 B.正方形ACFG的面积
C.正方形BCMN的面积 D.△ABC的面积
5.△ABC在下列条件下不是直角三角形的是( )
A.b2=a2﹣c2 B.a2:b2:c2=1:2:3
C.∠A:∠B:∠C=3:4:5 D.∠A=∠B﹣∠C
6.已知△ABC的三边长分别是6,8,10,则△ABC的面积是( )
A.12 B.15 C.20 D.24
7.下列各组数为勾股数的是( )
A.6,12,13 B.10,24,26 C.3,4,7 D.8,15,16
8.如图,为了求出湖两岸A、B两点之间的距离,观测者从测点A、B分别测得∠BAC=90°,又量得AC=9m,BC=15m,则A、B两点之间的距离为( )
A.10m B.11m C.12m D.13m
9.如图,将一根长为20cm的筷子置于底面直径为5cm,高为12cm的圆柱形水杯中,筷子露在杯子外面的长度为( )
A.13cm B.8cm C.7cm D.15cm
10.如图,若圆柱的底面周长是50cm,高是120cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处,则这条丝线的最小长度是( )
A.170cm B.70cm C.145cm D.130cm
11.如图,在正方形网格中,每个小正方形的边长都为1,点A、B、C在小正方形的格点上,连接AB,BC,则∠ABC= .
12.我们规定:经过三角形的一个顶点且将三角形的周长分成相等的两部分的直线叫做该三角形的“等周线”,“等周线”被这个三角形截得的线段叫做该三角形的“等周径”.例如等边三角形的边长为2,则它的“等周径”长为.在中Rt△ABC中,∠C=90°,AC=4,BC=3,若直线l为Rt△ABC的“等周线”,请直接写出△ABC的所有“等周径”长为 .
13.如图,四个全等的直角三角形围成一个大正方形ABCD,中间阴影的部分是一个小正方形EFGH,这样就组成了一个“赵爽弦图”.若AB=13,AE=12,则正方形EFGH的面积为 .
14.如图所示的网格是正方形网格,每个小正方形的边长均为1,点A,B,C,D都在格点上,则∠DAB+∠CAB的度数是 度.
15.在四边形ABCD中,∠C=90°,CD=8,BC=6,AB=24,AD=26,则四边形ABCD面积为 .
16.如图所示的网格是正方形网格,则∠ACB﹣∠DCE= °(点A、B、C、D、E是网格线交点).
17.如图,△ABC中,AC=b,BC=a,CD⊥AB于D.
(1)若a=b=13,AB=10,求CD的长;
(2)若∠ACB=90°,CD=4,求AD×DB的值;
(3)若CD2=AD×DB,判断△ABC的形状,并说明理由.
18.已知:如图等腰△ABC中,AB=AC,BC=10,BD⊥AC于D,且BD=8.求△ABC的面积S△ABC.
19.如图是用硬纸板做成的四个全等的直角三角形,两直角边的长分别为a和b,斜边长为c.请你开动脑筋,用它们拼出正方形图案,要求拼图时直角三角形纸片不能互相重叠.
(1)请你画出拼成的这个图形的示意图;
(2)利用(1)中画出的图形证明勾股定理.
20.现有三块两直角边长分别为1和2的直角三角形纸板,借助下面5×5的网格,用全部纸板分别拼出3个面积为3且周长不同的四边形,并写出相应四边形的周长.
21.如图1,方格纸中的每个小正方形的边长均为1,小正方形的顶点称为格点.已知A、B、C都是格点.
(1)小明发现图2中∠ABC是直角,请在图1补全他的思路;
(2)请借助图3用一种不同于小明的方法说明∠ABC是直角.
22.如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点都在格点上
(1)直接写出边AB、AC、BC的长.
(2)判断△ABC的形状,并说明理由.
23.我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下一组勾股数: ;
(2)若第一个数用字母n(n为奇数,且n≥3)表示,那么后两个数用含n的代数式分别表示为 和 ,请用所学知识说明它们是一组勾股数.
24.如图,学校有一块三角形空地ABC,计划将这块三角形空地分割成四边形ABDE和△EDC,分别摆放“秋海棠”和“天竺葵”两种不同的花卉.经测量,∠EDC=90°,DC=6m,CE=10m,BD=14m,AB=16m,AE=2m.
(1)求DE的长;
(2)求四边形ABDE的面积.
25.在某段公路的正上方有一摄像头A距离地面7米,一天李叔叔驾驶的汽车正沿公路笔直匀速驶来,当行驶到B点时第一次摄像,此时AB两点相距25米,1.5秒后第二次摄像汽车恰好行驶到A点正下方C点,已知该路段限速60km/h,请判断李叔叔是否超速,说明理由.
参考答案
1.解:分两种情况:(1)当点P在线段OC上时,
设t时后△POQ是等腰三角形,
有OP=OC﹣CP=OQ,
即12﹣2t=t,
解得,t=4;
(2)当点P在CO的延长线上时,此时经过CO时的时间已用6s,
当△POQ是等腰三角形时,∵∠POQ=60°,
∴△POQ是等边三角形,
∴OP=OQ,
即2(t﹣6)=t,
解得,t=12,
故选:B.
2.解:①若直角边长分别为1cm、2cm,
则由勾股定理可得斜边长为:=(cm);
②若斜边为2cm,则第三边为直角边,由勾股定理得:
=(cm).
综上,第三边的长为cm或cm.
故选:D.
3.解:∵AE=10,BE=24,即24和10为两条直角边长时,
∴小正方形的边长=24﹣10=14,
∴EF2=142+142=392,
故选:C.
4.解:∵∠BAC=90°,
∴AB2+AC2=BC2,
即S正方形ABDE+S正方形ACFG=S正方形BCMN,
∴S阴影=2S△ABC,
故选:D.
5.解:A.∵b2=a2﹣c2,
∴b2+c2=a2,
即△ABC是直角三角形,故本选项不符合题意;
B.∵a2:b2:c2=1:2:3,
∴a2+b2=c2,
即△ABC是直角三角形,故本选项不符合题意;
C.∵∠A:∠B:∠C=3:4:5,∠A+∠B+∠C=180°,
∴最大角∠C=×180°=75°<90°,
∴△ABC不是直角三角形,故本选项符合题意;
D.∵∠A=∠B﹣∠C,
∴∠A+∠C=∠B,
又∵∠A+∠B+∠C=180°,
∴2∠B=180°,
∴∠B=90°,
∴△ABC是直角三角形,故本选项不符合题意;
故选:C.
6.解:∵△ABC的三边长分别是6,8,10,
∴62+82=102,
∴△ABC是直角三角形,
∴△ABC的面积是=24,
故选:D.
7.解:A.∵62+122≠132,
∴6,12,13不是勾股数,故本选项不符合题意;
B.∵102+242=262,
∴10,24,26是勾股数,故本选项符合题意;
C.∵32+42≠72,
∴3,4,7不是勾股数,故本选项不符合题意;
D.∵82+152≠162,
∴8,15,16不是勾股数,故本选项不符合题意;
故选:B.
8.解:∵∠BAC=90°,AC=9m,BC=15m,
∴AB=(m),
故选:C.
9.解:由题意可得:
杯子内的筷子长度为:=13,
则筷子露在杯子外面的筷子长度为:20﹣13=7(cm).
故选:C.
10.解:如图,圆柱侧面展开图是矩形,
矩形的长为120cm,宽为圆柱的底面周长50cm,
根据勾股定理得:
AB==130(cm),
根据两点之间线段最短,可得丝线的最小长度为130cm,
故选:D.
11.解:连接AC,
由勾股定理得:AB=AC=,BC=,
∴BC2=AC2+AB2,
∴△ABC是直角三角形,
∵AB=AC,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,
故答案为:45°.
12.解:分三种情况讨论:
①当“等周线”经过点C时,直线1交AB于点E,
设BE=x,则AE=5﹣x,
作CH⊥AB于H,
由题意:3+x=4+5﹣x,
解得:x=3,
∵CH==,
∴BH==,
∴EH=3﹣=,
在Rt△ECH中,
CE==,
∴“等周径”长为;
②当“等周径”经过点A时,直线l交BC于点E,设BE=x,则CE=3﹣x,
由题意得:4+3﹣x=5+x,
解得:x=1,
∴EC=2,
在Rt△ACE中,
AE==2,
∴“等周径”长为2;
③当∴“等周径”经过点B时,直线l交AC于点E,
设AE=x,则CE=4﹣x,
由题意:3+4﹣x=5+x,
解得:x=1,
CE=3,
在Rt△BCE中,
BE==3,
∴“等周径”长为3,
故答案为:或2或3.
13.解:直角三角形直角边的较短边为,
正方形EFGH的面积=13×13﹣4×=169﹣120=49.
故答案为:49.
14.解:作C点关于AB的对称点E,连接AE,DE,如图所示:
∴∠CAB=∠EAB,
由勾股定理得:AD=,DE=,AE=,
∴AD2+DE2=AE2,
∴△AED是直角三角形,
∵AD=DE,
∴∠DAE=45°=∠DAB+∠BAE=∠DAB+∠CAB,
故答案为:45.
15.解:如图,连接BD,
∵∠C=90°,
∴BD==10,
∵BD2+AB2=102+242=262=AD2,
∴∠ABD=90°,
∴四边形ABCD的面积=S△ABD+S△BCD==144.
故答案为:144
16.解:如图,连接CG、AG,
由勾股定理得:AG2=CG2=12+22=5,AC2=12+32=10,
∴AG2+CG2=AC2,
∴∠CGA=90°,
∴△CAG是等腰直角三角形,
∴∠CAG=45°,
∵AF∥BC,
∴∠CAF=∠BCA,
在△AFG和△CDE中,
,
∴△AFG≌△CDE(SAS),
∴∠FAG=∠DCE,
∴∠ACB﹣∠DCE=∠CAF﹣∠FAG=∠CAG=45°.
故答案为:45.
17.解:(1)∵AC=BC,CD⊥AB,
∴AD=BD=5,
在Rt△ADC中,
CD==12.
(2在Rt△ACD中,由勾股定理得,
AC2﹣AD2=CD2=16①,
在Rt△BCD中,由勾股定理得,
BC2﹣BD2=CD2=16②,
联立①和②得:AC2+BC2﹣(AD2+BD2)=32,
∵AC2+BC2=AB2,AD2+BD2=(AD+BD)2﹣2AD BD,
∴AB2﹣AB2+2AD BD=32,
∴2AD BD=32,
∴AD BD=16;
(3)∵CD2=AD DB,
∴AC2﹣AD2=AD BD,
BC2﹣BD2=AD BD,
∴AC2﹣AD2+BC2﹣BD2=2AD BD,
∴AC2+BC2=AD2+BD2+2AD BD,
∴AC2+BC2=(AD+BD)2,
即AC2+BC2=AB2,
∴△ABC是直角三角形.
18.解:∵BD⊥AC,
在Rt△BCD中,BD=8,BC=10,
∴CD=6,
设AB=AC=x,
则AD=x﹣6,
在Rt△ABD中,AD2+BD2=AB2,
∴(x﹣6)2+82=x2,
∴x=,
∴.
19.解:(1)(答案不唯一)如图;
(2)证明:∵大正方形的面积可表示为(a+b)2,
大正方形的面积也可表示为:c2+4×ab,
∴(a+b)2=c2+4×ab,
即a2+b2+2ab=c2+2ab,
∴a2+b2=c2,
即直角三角形两直角边的平方和等于斜边的平方.
20.解;如图所示:
21.解:(1)∵AB=,
BC=,
AC=,
∴AB2+BC2=AC2,根据勾股定理的逆定理,
∴△ABC是直角三角形,
∴∠ABC=90°,
故答案为:,2,AB2+BC2=AC2,勾股定理的逆定理;
(2)过A点作AD⊥BE于D,过C作CE⊥DB于E,
由图可知:AD=BE,BD=CE,∠ADB=∠BEC=90°,
在△ADB和△BEC中,
,
∴△ADB≌△BEC(SAS),
∴∠ABD=∠BCE,
在△BEC中,∠BEC+∠BCE+∠EBC=180°,
∴∠BCE+∠EBC=180°﹣∠BEC=90°,
∴∠ABD+∠EBC=90°,
∵D,B,E三点共线,
∴∠ABD+∠EBC+∠ABC=180°,
∴∠ABC=180°﹣(∠ABD+∠EBC)=90°,
∴∠ABC是直角.
22.解:(1)由勾股定理得:AB==,AC==2,BC==5;
(2)∵AB=,AC=2,BC=5,
∴AB2+AC2=BC2,
∴∠BAC=90°,
即△ABC是直角三角形.
23.解:(1)11,60,61;
(2)后两个数表示为和,
∵,,
∴.
又∵n≥3,且n为奇数,
∴由n,,三个数组成的数是勾股数.
故答案为:11,60,61.
24.解:(1)在Rt△EDC中,∠EDC=90°,DC=6m,CE=10m,
∴m;
(2)如图,连接BE,
在Rt△EBD中,BD=14m,ED=8m,
∴BE2=BD2+ED2=142+82=260,
∵AB=16m,AE=2m,
∴AB2+AE2=162+22=260,
∴AB2+AE2=BE2,
∴△ABE是直角三角形,∠A=90°,
∴S△ABE=×16×2=16(m2).
又∵S△BDE=×14×8=56(m2).
∴四边形ABDE的面积=S△ABE+S△BDE=72(m2).
25.解:李叔叔不超速,理由如下:
如图,
Rt△ABC中,AC=7,AB=25,
由勾股定理得:BC==24,
v=24÷1.5=16(m/s)=57.6(km/h),
∵57.6<60,
∴李叔叔不超速.
1.如图,∠AOB=60°,C是BO延长线上一点,OC=12cm,动点P从点C出发沿CB以2cm/s的速度移动,动点Q从点O出发沿OA以1cm/s的速度移动,如果点P,Q同时出发,用t表示移动的时间,若△POQ是等腰三角形,此时t的值是( )
A.6或12 B.4或12 C.4或6 D.6或8
2.在直角三角形中,若两条边的长分别是1cm、2cm,则第三边的长为( )
A.3cm B.cm C.2cm或cm D.cm或cm
3.如图所示的是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形
拼接而成,其中AE=10,BE=24,则EF2的值是( )
A.169 B.196 C.392 D.588
4.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图以直角三角形的各边为边分别向同侧作正方形,若知道图中阴影部分的面积之和,则一定能求出( )
A.正方形ABED的面积 B.正方形ACFG的面积
C.正方形BCMN的面积 D.△ABC的面积
5.△ABC在下列条件下不是直角三角形的是( )
A.b2=a2﹣c2 B.a2:b2:c2=1:2:3
C.∠A:∠B:∠C=3:4:5 D.∠A=∠B﹣∠C
6.已知△ABC的三边长分别是6,8,10,则△ABC的面积是( )
A.12 B.15 C.20 D.24
7.下列各组数为勾股数的是( )
A.6,12,13 B.10,24,26 C.3,4,7 D.8,15,16
8.如图,为了求出湖两岸A、B两点之间的距离,观测者从测点A、B分别测得∠BAC=90°,又量得AC=9m,BC=15m,则A、B两点之间的距离为( )
A.10m B.11m C.12m D.13m
9.如图,将一根长为20cm的筷子置于底面直径为5cm,高为12cm的圆柱形水杯中,筷子露在杯子外面的长度为( )
A.13cm B.8cm C.7cm D.15cm
10.如图,若圆柱的底面周长是50cm,高是120cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处,则这条丝线的最小长度是( )
A.170cm B.70cm C.145cm D.130cm
11.如图,在正方形网格中,每个小正方形的边长都为1,点A、B、C在小正方形的格点上,连接AB,BC,则∠ABC= .
12.我们规定:经过三角形的一个顶点且将三角形的周长分成相等的两部分的直线叫做该三角形的“等周线”,“等周线”被这个三角形截得的线段叫做该三角形的“等周径”.例如等边三角形的边长为2,则它的“等周径”长为.在中Rt△ABC中,∠C=90°,AC=4,BC=3,若直线l为Rt△ABC的“等周线”,请直接写出△ABC的所有“等周径”长为 .
13.如图,四个全等的直角三角形围成一个大正方形ABCD,中间阴影的部分是一个小正方形EFGH,这样就组成了一个“赵爽弦图”.若AB=13,AE=12,则正方形EFGH的面积为 .
14.如图所示的网格是正方形网格,每个小正方形的边长均为1,点A,B,C,D都在格点上,则∠DAB+∠CAB的度数是 度.
15.在四边形ABCD中,∠C=90°,CD=8,BC=6,AB=24,AD=26,则四边形ABCD面积为 .
16.如图所示的网格是正方形网格,则∠ACB﹣∠DCE= °(点A、B、C、D、E是网格线交点).
17.如图,△ABC中,AC=b,BC=a,CD⊥AB于D.
(1)若a=b=13,AB=10,求CD的长;
(2)若∠ACB=90°,CD=4,求AD×DB的值;
(3)若CD2=AD×DB,判断△ABC的形状,并说明理由.
18.已知:如图等腰△ABC中,AB=AC,BC=10,BD⊥AC于D,且BD=8.求△ABC的面积S△ABC.
19.如图是用硬纸板做成的四个全等的直角三角形,两直角边的长分别为a和b,斜边长为c.请你开动脑筋,用它们拼出正方形图案,要求拼图时直角三角形纸片不能互相重叠.
(1)请你画出拼成的这个图形的示意图;
(2)利用(1)中画出的图形证明勾股定理.
20.现有三块两直角边长分别为1和2的直角三角形纸板,借助下面5×5的网格,用全部纸板分别拼出3个面积为3且周长不同的四边形,并写出相应四边形的周长.
21.如图1,方格纸中的每个小正方形的边长均为1,小正方形的顶点称为格点.已知A、B、C都是格点.
(1)小明发现图2中∠ABC是直角,请在图1补全他的思路;
(2)请借助图3用一种不同于小明的方法说明∠ABC是直角.
22.如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点都在格点上
(1)直接写出边AB、AC、BC的长.
(2)判断△ABC的形状,并说明理由.
23.我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下一组勾股数: ;
(2)若第一个数用字母n(n为奇数,且n≥3)表示,那么后两个数用含n的代数式分别表示为 和 ,请用所学知识说明它们是一组勾股数.
24.如图,学校有一块三角形空地ABC,计划将这块三角形空地分割成四边形ABDE和△EDC,分别摆放“秋海棠”和“天竺葵”两种不同的花卉.经测量,∠EDC=90°,DC=6m,CE=10m,BD=14m,AB=16m,AE=2m.
(1)求DE的长;
(2)求四边形ABDE的面积.
25.在某段公路的正上方有一摄像头A距离地面7米,一天李叔叔驾驶的汽车正沿公路笔直匀速驶来,当行驶到B点时第一次摄像,此时AB两点相距25米,1.5秒后第二次摄像汽车恰好行驶到A点正下方C点,已知该路段限速60km/h,请判断李叔叔是否超速,说明理由.
参考答案
1.解:分两种情况:(1)当点P在线段OC上时,
设t时后△POQ是等腰三角形,
有OP=OC﹣CP=OQ,
即12﹣2t=t,
解得,t=4;
(2)当点P在CO的延长线上时,此时经过CO时的时间已用6s,
当△POQ是等腰三角形时,∵∠POQ=60°,
∴△POQ是等边三角形,
∴OP=OQ,
即2(t﹣6)=t,
解得,t=12,
故选:B.
2.解:①若直角边长分别为1cm、2cm,
则由勾股定理可得斜边长为:=(cm);
②若斜边为2cm,则第三边为直角边,由勾股定理得:
=(cm).
综上,第三边的长为cm或cm.
故选:D.
3.解:∵AE=10,BE=24,即24和10为两条直角边长时,
∴小正方形的边长=24﹣10=14,
∴EF2=142+142=392,
故选:C.
4.解:∵∠BAC=90°,
∴AB2+AC2=BC2,
即S正方形ABDE+S正方形ACFG=S正方形BCMN,
∴S阴影=2S△ABC,
故选:D.
5.解:A.∵b2=a2﹣c2,
∴b2+c2=a2,
即△ABC是直角三角形,故本选项不符合题意;
B.∵a2:b2:c2=1:2:3,
∴a2+b2=c2,
即△ABC是直角三角形,故本选项不符合题意;
C.∵∠A:∠B:∠C=3:4:5,∠A+∠B+∠C=180°,
∴最大角∠C=×180°=75°<90°,
∴△ABC不是直角三角形,故本选项符合题意;
D.∵∠A=∠B﹣∠C,
∴∠A+∠C=∠B,
又∵∠A+∠B+∠C=180°,
∴2∠B=180°,
∴∠B=90°,
∴△ABC是直角三角形,故本选项不符合题意;
故选:C.
6.解:∵△ABC的三边长分别是6,8,10,
∴62+82=102,
∴△ABC是直角三角形,
∴△ABC的面积是=24,
故选:D.
7.解:A.∵62+122≠132,
∴6,12,13不是勾股数,故本选项不符合题意;
B.∵102+242=262,
∴10,24,26是勾股数,故本选项符合题意;
C.∵32+42≠72,
∴3,4,7不是勾股数,故本选项不符合题意;
D.∵82+152≠162,
∴8,15,16不是勾股数,故本选项不符合题意;
故选:B.
8.解:∵∠BAC=90°,AC=9m,BC=15m,
∴AB=(m),
故选:C.
9.解:由题意可得:
杯子内的筷子长度为:=13,
则筷子露在杯子外面的筷子长度为:20﹣13=7(cm).
故选:C.
10.解:如图,圆柱侧面展开图是矩形,
矩形的长为120cm,宽为圆柱的底面周长50cm,
根据勾股定理得:
AB==130(cm),
根据两点之间线段最短,可得丝线的最小长度为130cm,
故选:D.
11.解:连接AC,
由勾股定理得:AB=AC=,BC=,
∴BC2=AC2+AB2,
∴△ABC是直角三角形,
∵AB=AC,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,
故答案为:45°.
12.解:分三种情况讨论:
①当“等周线”经过点C时,直线1交AB于点E,
设BE=x,则AE=5﹣x,
作CH⊥AB于H,
由题意:3+x=4+5﹣x,
解得:x=3,
∵CH==,
∴BH==,
∴EH=3﹣=,
在Rt△ECH中,
CE==,
∴“等周径”长为;
②当“等周径”经过点A时,直线l交BC于点E,设BE=x,则CE=3﹣x,
由题意得:4+3﹣x=5+x,
解得:x=1,
∴EC=2,
在Rt△ACE中,
AE==2,
∴“等周径”长为2;
③当∴“等周径”经过点B时,直线l交AC于点E,
设AE=x,则CE=4﹣x,
由题意:3+4﹣x=5+x,
解得:x=1,
CE=3,
在Rt△BCE中,
BE==3,
∴“等周径”长为3,
故答案为:或2或3.
13.解:直角三角形直角边的较短边为,
正方形EFGH的面积=13×13﹣4×=169﹣120=49.
故答案为:49.
14.解:作C点关于AB的对称点E,连接AE,DE,如图所示:
∴∠CAB=∠EAB,
由勾股定理得:AD=,DE=,AE=,
∴AD2+DE2=AE2,
∴△AED是直角三角形,
∵AD=DE,
∴∠DAE=45°=∠DAB+∠BAE=∠DAB+∠CAB,
故答案为:45.
15.解:如图,连接BD,
∵∠C=90°,
∴BD==10,
∵BD2+AB2=102+242=262=AD2,
∴∠ABD=90°,
∴四边形ABCD的面积=S△ABD+S△BCD==144.
故答案为:144
16.解:如图,连接CG、AG,
由勾股定理得:AG2=CG2=12+22=5,AC2=12+32=10,
∴AG2+CG2=AC2,
∴∠CGA=90°,
∴△CAG是等腰直角三角形,
∴∠CAG=45°,
∵AF∥BC,
∴∠CAF=∠BCA,
在△AFG和△CDE中,
,
∴△AFG≌△CDE(SAS),
∴∠FAG=∠DCE,
∴∠ACB﹣∠DCE=∠CAF﹣∠FAG=∠CAG=45°.
故答案为:45.
17.解:(1)∵AC=BC,CD⊥AB,
∴AD=BD=5,
在Rt△ADC中,
CD==12.
(2在Rt△ACD中,由勾股定理得,
AC2﹣AD2=CD2=16①,
在Rt△BCD中,由勾股定理得,
BC2﹣BD2=CD2=16②,
联立①和②得:AC2+BC2﹣(AD2+BD2)=32,
∵AC2+BC2=AB2,AD2+BD2=(AD+BD)2﹣2AD BD,
∴AB2﹣AB2+2AD BD=32,
∴2AD BD=32,
∴AD BD=16;
(3)∵CD2=AD DB,
∴AC2﹣AD2=AD BD,
BC2﹣BD2=AD BD,
∴AC2﹣AD2+BC2﹣BD2=2AD BD,
∴AC2+BC2=AD2+BD2+2AD BD,
∴AC2+BC2=(AD+BD)2,
即AC2+BC2=AB2,
∴△ABC是直角三角形.
18.解:∵BD⊥AC,
在Rt△BCD中,BD=8,BC=10,
∴CD=6,
设AB=AC=x,
则AD=x﹣6,
在Rt△ABD中,AD2+BD2=AB2,
∴(x﹣6)2+82=x2,
∴x=,
∴.
19.解:(1)(答案不唯一)如图;
(2)证明:∵大正方形的面积可表示为(a+b)2,
大正方形的面积也可表示为:c2+4×ab,
∴(a+b)2=c2+4×ab,
即a2+b2+2ab=c2+2ab,
∴a2+b2=c2,
即直角三角形两直角边的平方和等于斜边的平方.
20.解;如图所示:
21.解:(1)∵AB=,
BC=,
AC=,
∴AB2+BC2=AC2,根据勾股定理的逆定理,
∴△ABC是直角三角形,
∴∠ABC=90°,
故答案为:,2,AB2+BC2=AC2,勾股定理的逆定理;
(2)过A点作AD⊥BE于D,过C作CE⊥DB于E,
由图可知:AD=BE,BD=CE,∠ADB=∠BEC=90°,
在△ADB和△BEC中,
,
∴△ADB≌△BEC(SAS),
∴∠ABD=∠BCE,
在△BEC中,∠BEC+∠BCE+∠EBC=180°,
∴∠BCE+∠EBC=180°﹣∠BEC=90°,
∴∠ABD+∠EBC=90°,
∵D,B,E三点共线,
∴∠ABD+∠EBC+∠ABC=180°,
∴∠ABC=180°﹣(∠ABD+∠EBC)=90°,
∴∠ABC是直角.
22.解:(1)由勾股定理得:AB==,AC==2,BC==5;
(2)∵AB=,AC=2,BC=5,
∴AB2+AC2=BC2,
∴∠BAC=90°,
即△ABC是直角三角形.
23.解:(1)11,60,61;
(2)后两个数表示为和,
∵,,
∴.
又∵n≥3,且n为奇数,
∴由n,,三个数组成的数是勾股数.
故答案为:11,60,61.
24.解:(1)在Rt△EDC中,∠EDC=90°,DC=6m,CE=10m,
∴m;
(2)如图,连接BE,
在Rt△EBD中,BD=14m,ED=8m,
∴BE2=BD2+ED2=142+82=260,
∵AB=16m,AE=2m,
∴AB2+AE2=162+22=260,
∴AB2+AE2=BE2,
∴△ABE是直角三角形,∠A=90°,
∴S△ABE=×16×2=16(m2).
又∵S△BDE=×14×8=56(m2).
∴四边形ABDE的面积=S△ABE+S△BDE=72(m2).
25.解:李叔叔不超速,理由如下:
如图,
Rt△ABC中,AC=7,AB=25,
由勾股定理得:BC==24,
v=24÷1.5=16(m/s)=57.6(km/h),
∵57.6<60,
∴李叔叔不超速.
