沪科版数学七年级上册 3.3二元一次方程组 课件(共14张PPT)
文档属性
| 名称 | 沪科版数学七年级上册 3.3二元一次方程组 课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 740.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
二元一次方程组及其解法
(第二课时)
---用代入消元法解二元一次方程组
“一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
——法国数学家 笛卡儿[Descartes, 1596-1650 ]
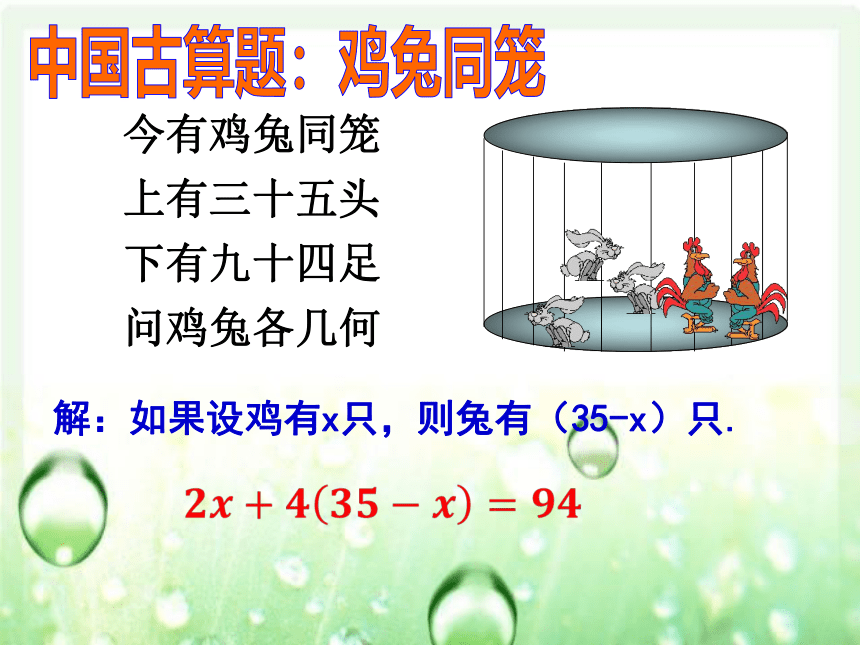
今有鸡兔同笼
上有三十五头
下有九十四足
问鸡兔各几何
解:如果设鸡有x只,则兔有(35-x)只.
今有鸡兔同笼
上有三十五头
下有九十四足
问鸡兔各几何
解:如果设鸡有x只,兔有y只.
解:设鸡有x只,兔有y只.
解:设鸡有x只,则兔有(35-x)只.
思考1:上面的一元一次方程和二元一次方程组有什么关系
思考2:如何求解二元一次方程组呢
解方程组
解:
①
②
由①得:
y =
③
把③代入②得:
2x+ 4(35-x)= 94
把x= 23代入③,得
y = 12
x +y = 35
2x +4 y = 94
2x+140– 4x= 94
– 2x= -46
x= 23
∴方程组的解是
x =23
y =12
三、重难点突破----探究一
35-x
把③代入①可以吗?试试看!
把y=12代入① 或②可以吗?
如何判断是不是方程组的解?
代入消元法就是从一个方程中求出某一个未知数的 ,再把它“代入”到 ,进行求解,这种解二元一次方程组的方法,称为代入消元法,简称 。
注:代入消元法体现的是一种转化的思想,我们是把二元一次方程通过变形转化成了一元一次方程,从而进行求解。
代数式
另外一个方程
代入法
解方程组
①
②
x +y = 35
2x +4 y = 94
三、重难点突破----探究一
想一想:把方程①变形时能不能用含y的代数式表示x来解呢?
试一试:请同学们自己动手来试一试吧?
解方程组
解:
①
②
由①得:
x = 35-y
③
把③代入②得:
2(35-y)+4y= 94
把y=12代入③,得
x = 23
1、将方程组里的一个方程变形,用含有一个未知数的代数式表示另一个未知数;
2、用这个代数式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
用代入法解二元一次方程组的一般步骤
变
代
求
写
x +y = 35
2x +4 y = 94
70-2y+4y= 94
2y= 24
y= 12
∴方程组的解是
x =23
y =12
三、重难点突破----探究一
用代入法解方程组:
三、重难点突破----探究二
通过计算你能发现什么?
四、巩固新知
五、拓展提升 :
今有鸡兔同笼
上有三十五头
下有九十四足
问鸡兔各几何
解:如果设鸡有x只,兔有y只,
x+y=35
2x+4y=94
课堂小结
谢谢大家!
二元一次方程组及其解法
(第二课时)
---用代入消元法解二元一次方程组
“一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
——法国数学家 笛卡儿[Descartes, 1596-1650 ]
今有鸡兔同笼
上有三十五头
下有九十四足
问鸡兔各几何
解:如果设鸡有x只,则兔有(35-x)只.
今有鸡兔同笼
上有三十五头
下有九十四足
问鸡兔各几何
解:如果设鸡有x只,兔有y只.
解:设鸡有x只,兔有y只.
解:设鸡有x只,则兔有(35-x)只.
思考1:上面的一元一次方程和二元一次方程组有什么关系
思考2:如何求解二元一次方程组呢
解方程组
解:
①
②
由①得:
y =
③
把③代入②得:
2x+ 4(35-x)= 94
把x= 23代入③,得
y = 12
x +y = 35
2x +4 y = 94
2x+140– 4x= 94
– 2x= -46
x= 23
∴方程组的解是
x =23
y =12
三、重难点突破----探究一
35-x
把③代入①可以吗?试试看!
把y=12代入① 或②可以吗?
如何判断是不是方程组的解?
代入消元法就是从一个方程中求出某一个未知数的 ,再把它“代入”到 ,进行求解,这种解二元一次方程组的方法,称为代入消元法,简称 。
注:代入消元法体现的是一种转化的思想,我们是把二元一次方程通过变形转化成了一元一次方程,从而进行求解。
代数式
另外一个方程
代入法
解方程组
①
②
x +y = 35
2x +4 y = 94
三、重难点突破----探究一
想一想:把方程①变形时能不能用含y的代数式表示x来解呢?
试一试:请同学们自己动手来试一试吧?
解方程组
解:
①
②
由①得:
x = 35-y
③
把③代入②得:
2(35-y)+4y= 94
把y=12代入③,得
x = 23
1、将方程组里的一个方程变形,用含有一个未知数的代数式表示另一个未知数;
2、用这个代数式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
用代入法解二元一次方程组的一般步骤
变
代
求
写
x +y = 35
2x +4 y = 94
70-2y+4y= 94
2y= 24
y= 12
∴方程组的解是
x =23
y =12
三、重难点突破----探究一
用代入法解方程组:
三、重难点突破----探究二
通过计算你能发现什么?
四、巩固新知
五、拓展提升 :
今有鸡兔同笼
上有三十五头
下有九十四足
问鸡兔各几何
解:如果设鸡有x只,兔有y只,
x+y=35
2x+4y=94
课堂小结
谢谢大家!
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
