沪科版数学七年级上册 4.5 角的比较与补(余)角 课件(共17张PPT)
文档属性
| 名称 | 沪科版数学七年级上册 4.5 角的比较与补(余)角 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 19:27:14 | ||
图片预览



文档简介
(共17张PPT)
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。 ——毕达哥拉斯
创设情境 引入新课
你能比较这两个角的大小吗?
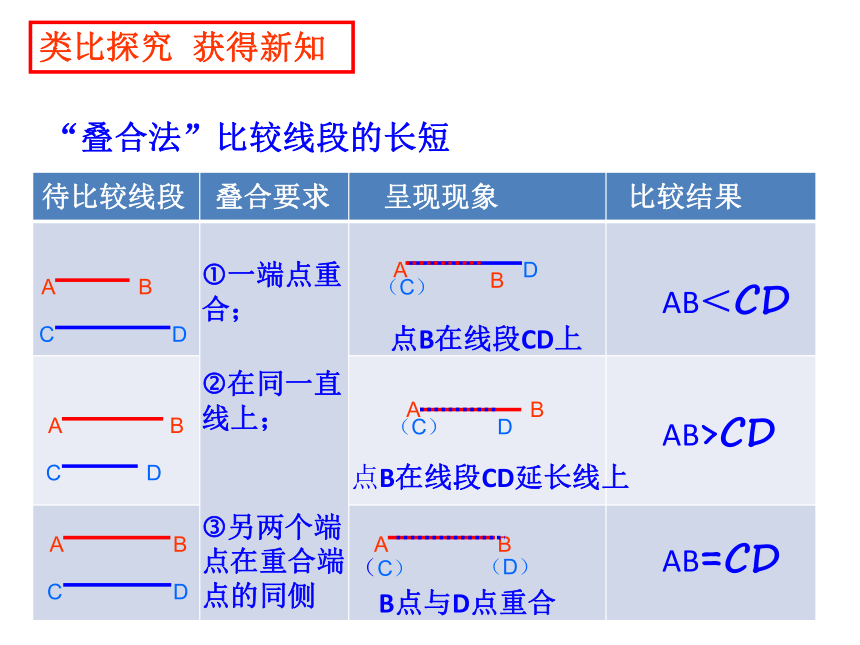
待比较线段 叠合要求 呈现现象 比较结果
A
B
C
D
A
B
C
D
A
B
C
D
A
B
(C)
(D)
一端点重合;
在同一直线上;
另两个端点在重合端点的同侧
D
A
B
(C)
点B在线段CD上
(C)
D
A
B
点B在线段CD延长线上
AB<CD
AB>CD
B点与D点重合
AB=CD
“叠合法”比较线段的长短
类比探究 获得新知
顶点重合;
一边重合;
另两条边在重合边的同侧.
AB在∠DEF 内部
∠ABC<∠DEF
AB与ED重合
“叠合法”比较角度的大小
类比探究 获得新知
待比较角
叠合要求
呈现现象
比较结果
F
E
D
B
C
A
C
B
D
(E)
(F)
A
AB在∠DEF 外部
∠ABC>∠DEF
F
E
D
B
C
A
(E)
(F)
(A)
D
B
D
F
E
C
B
D
A
∠ABC=∠DEF
请类比“叠合法”比较线段的长短的方法,来比较角的大小
(E)
(F)
A
B
D
C
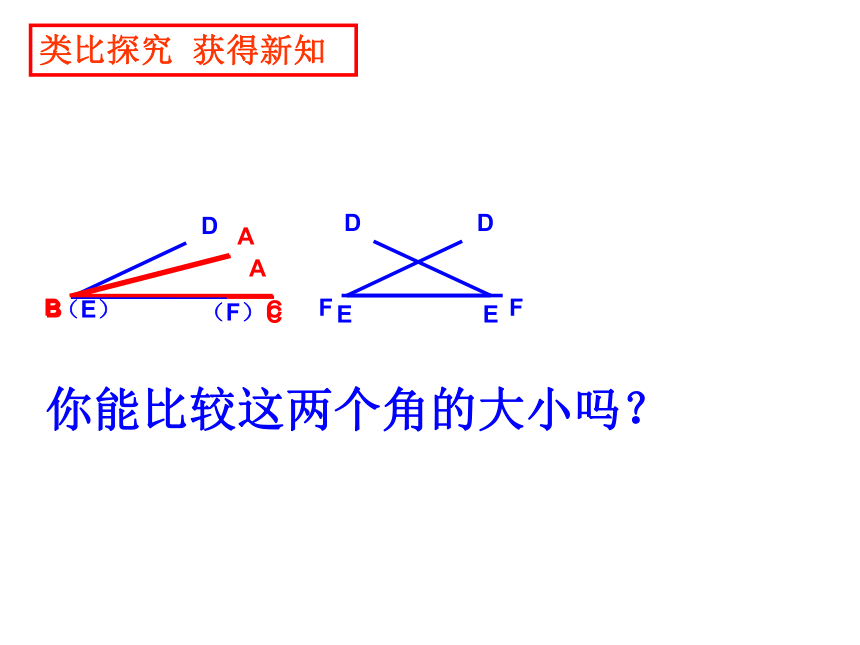
你能比较这两个角的大小吗?
类比探究 获得新知
D
C
B
A
(E)
(F)
A
B
C
D
E
F
D
E
F
A
C
B
E
F
D
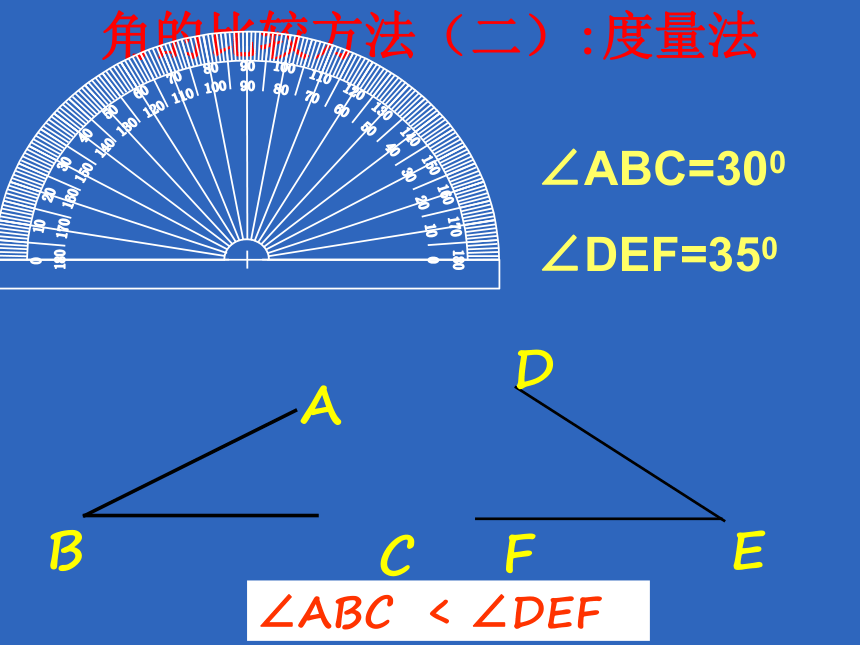
∠ABC < ∠DEF
角的比较方法(二):度量法
∠ABC=300
∠DEF=350
类比探究 获得新知
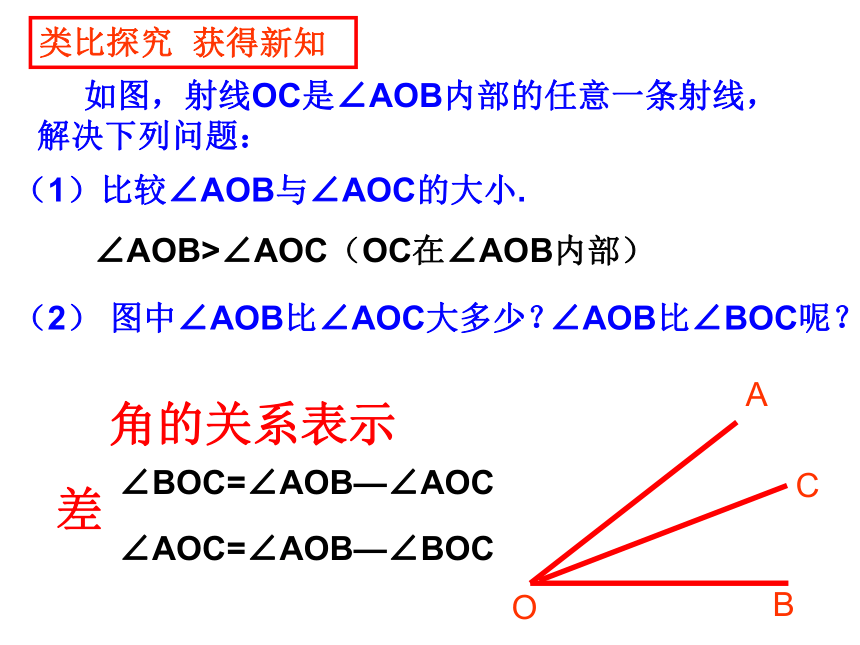
(1)比较∠AOB与∠AOC的大小.
如图,射线OC是∠AOB内部的任意一条射线,
解决下列问题:
∠AOB>∠AOC(OC在∠AOB内部)
C
A
O
B
(2) 图中∠AOB比∠AOC大多少?
∠BOC=∠AOB—∠AOC
∠AOC=∠AOB—∠BOC
角的关系表示
差
∠AOB比∠BOC呢?
如图,射线OC是∠AOB内部的任意一条射线,
解决下列问题:
(3) 图中∠AOB又可怎样表示?
∠AOB=∠AOC+∠BOC
和
(4) 假如将射线OC在∠AOB内绕点O顺时针旋转,∠AOC 与∠BOC会有怎样的变化?
动手做一做
问题:一张透明的纸,在上面作任意角∠AOB,你能把这个角分成两个相等的角吗?
方法:对折,使角的两边OA与OB重合,然后把这张纸展开、铺平,画出折痕OC。
A
O
B
C
请给上图射线OC取个合适的名称?
互动探究 认识新知
在角的内部,以角的顶点为端点的一条射线把这个角分成两个相等的角,这条射线叫做这个角的平分线.
如右图所示:
分
倍
角的表示:倍与分
例题讲解 巩固新知
如图,已知OE是∠BOC的平分线,OD是∠AOC的平分线,且∠AOB=150°,求∠DOE的度数。
D C
A
B
E
O
1:填空:
如图,从点O分别引4条射线OA,OB,OC,OD.
则 ∠AOC= _____+_____;
∠AOB= _____—_____;
∠COD= _____+______—_____;
∠BOC= _____+______—_____—______.
课堂练习 巩固新知
A
D
C
O
B
课堂练习 巩固新知
1、按下列要求画图、计算:
⑴画∠AOB=90°;
⑵在∠AOB外画∠BOC=30°;
⑶分别画∠AOB,∠BOC的角平分线OD、OE;
⑷求 ∠AOC,∠EOD的度数.
变式练习 拓展新知
O
A
D
B
C
E
变式1:如图,如果∠AOB=80 °,∠BOC=20°,
OD、OE分别为∠AOB,∠BOC的角平分线,则
∠AOC= ,∠EOD= .
变式2:如果∠AOB=α,∠BOC=β,OD、OE分别为∠AOB,∠BOC的角平分线,你能说出∠AOC与∠EOD度数的度数吗?
100
50
变式2:按下列要求画图、计算:
⑴画∠AOB=90°;
改为“画∠BOC=30°”
⑶分别画∠AOB,∠BOC的角平分线OD、OE;
⑷求 ∠AOC,∠EOD的度数.
变式练习 拓展新知
⑵在∠AOB外画∠BOC=30°;
课堂总结 构建新知
本节课你学了哪些知识?你有哪些收获和体会?
提出问题
怎样比较角的大小
抽象
回忆线段大小的比较
分析问题
解决问题
角的和、差的意义,角平分线定义
度量法、叠合法比较角的大小
知识迁延
应用
应用
类比
布置作业 巩固反馈
必做题:习题4.5 第1-4题;
选做题:用一副三角板可以画出多少个小于平
角的角?动手试一试.
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。 ——毕达哥拉斯
创设情境 引入新课
你能比较这两个角的大小吗?
待比较线段 叠合要求 呈现现象 比较结果
A
B
C
D
A
B
C
D
A
B
C
D
A
B
(C)
(D)
一端点重合;
在同一直线上;
另两个端点在重合端点的同侧
D
A
B
(C)
点B在线段CD上
(C)
D
A
B
点B在线段CD延长线上
AB<CD
AB>CD
B点与D点重合
AB=CD
“叠合法”比较线段的长短
类比探究 获得新知
顶点重合;
一边重合;
另两条边在重合边的同侧.
AB在∠DEF 内部
∠ABC<∠DEF
AB与ED重合
“叠合法”比较角度的大小
类比探究 获得新知
待比较角
叠合要求
呈现现象
比较结果
F
E
D
B
C
A
C
B
D
(E)
(F)
A
AB在∠DEF 外部
∠ABC>∠DEF
F
E
D
B
C
A
(E)
(F)
(A)
D
B
D
F
E
C
B
D
A
∠ABC=∠DEF
请类比“叠合法”比较线段的长短的方法,来比较角的大小
(E)
(F)
A
B
D
C
你能比较这两个角的大小吗?
类比探究 获得新知
D
C
B
A
(E)
(F)
A
B
C
D
E
F
D
E
F
A
C
B
E
F
D
∠ABC < ∠DEF
角的比较方法(二):度量法
∠ABC=300
∠DEF=350
类比探究 获得新知
(1)比较∠AOB与∠AOC的大小.
如图,射线OC是∠AOB内部的任意一条射线,
解决下列问题:
∠AOB>∠AOC(OC在∠AOB内部)
C
A
O
B
(2) 图中∠AOB比∠AOC大多少?
∠BOC=∠AOB—∠AOC
∠AOC=∠AOB—∠BOC
角的关系表示
差
∠AOB比∠BOC呢?
如图,射线OC是∠AOB内部的任意一条射线,
解决下列问题:
(3) 图中∠AOB又可怎样表示?
∠AOB=∠AOC+∠BOC
和
(4) 假如将射线OC在∠AOB内绕点O顺时针旋转,∠AOC 与∠BOC会有怎样的变化?
动手做一做
问题:一张透明的纸,在上面作任意角∠AOB,你能把这个角分成两个相等的角吗?
方法:对折,使角的两边OA与OB重合,然后把这张纸展开、铺平,画出折痕OC。
A
O
B
C
请给上图射线OC取个合适的名称?
互动探究 认识新知
在角的内部,以角的顶点为端点的一条射线把这个角分成两个相等的角,这条射线叫做这个角的平分线.
如右图所示:
分
倍
角的表示:倍与分
例题讲解 巩固新知
如图,已知OE是∠BOC的平分线,OD是∠AOC的平分线,且∠AOB=150°,求∠DOE的度数。
D C
A
B
E
O
1:填空:
如图,从点O分别引4条射线OA,OB,OC,OD.
则 ∠AOC= _____+_____;
∠AOB= _____—_____;
∠COD= _____+______—_____;
∠BOC= _____+______—_____—______.
课堂练习 巩固新知
A
D
C
O
B
课堂练习 巩固新知
1、按下列要求画图、计算:
⑴画∠AOB=90°;
⑵在∠AOB外画∠BOC=30°;
⑶分别画∠AOB,∠BOC的角平分线OD、OE;
⑷求 ∠AOC,∠EOD的度数.
变式练习 拓展新知
O
A
D
B
C
E
变式1:如图,如果∠AOB=80 °,∠BOC=20°,
OD、OE分别为∠AOB,∠BOC的角平分线,则
∠AOC= ,∠EOD= .
变式2:如果∠AOB=α,∠BOC=β,OD、OE分别为∠AOB,∠BOC的角平分线,你能说出∠AOC与∠EOD度数的度数吗?
100
50
变式2:按下列要求画图、计算:
⑴画∠AOB=90°;
改为“画∠BOC=30°”
⑶分别画∠AOB,∠BOC的角平分线OD、OE;
⑷求 ∠AOC,∠EOD的度数.
变式练习 拓展新知
⑵在∠AOB外画∠BOC=30°;
课堂总结 构建新知
本节课你学了哪些知识?你有哪些收获和体会?
提出问题
怎样比较角的大小
抽象
回忆线段大小的比较
分析问题
解决问题
角的和、差的意义,角平分线定义
度量法、叠合法比较角的大小
知识迁延
应用
应用
类比
布置作业 巩固反馈
必做题:习题4.5 第1-4题;
选做题:用一副三角板可以画出多少个小于平
角的角?动手试一试.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
