鲁教版(五四制)数学七年级上册 3.1 探索勾股定理-第二课时 课件(共21张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学七年级上册 3.1 探索勾股定理-第二课时 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 583.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
第二课时
探索勾股定理
Contents
目录
01
02
03
04
复习旧知
巩固练习
课堂小结
新知探究
问题解决
05
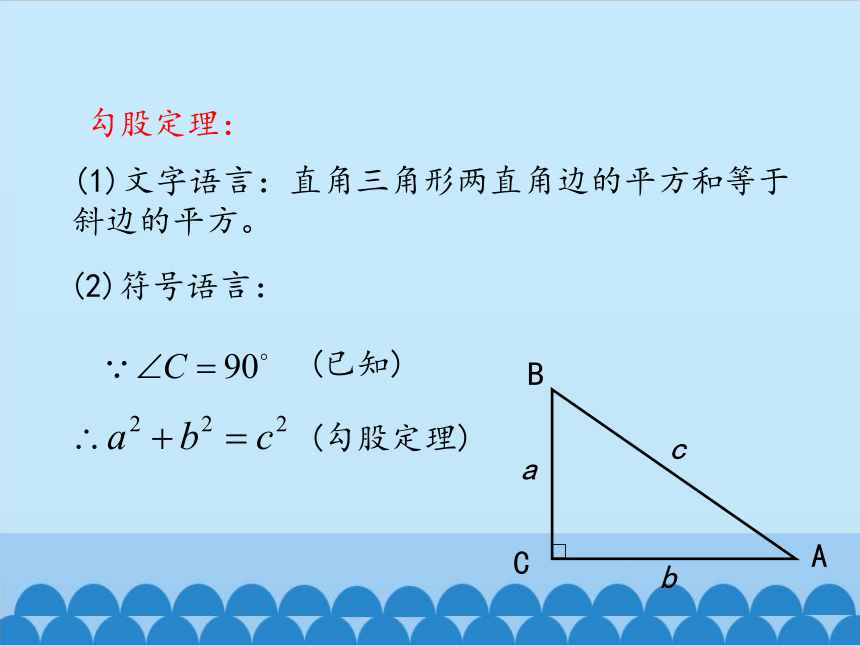
勾股定理:
(1)文字语言:直角三角形两直角边的平方和等于斜边的平方。
A
B
C
a
b
c
(2)符号语言:
(已知)
(勾股定理)
上一节课,我们通过测量和数格子的方法发现了勾股定理,在图中,分别以直角三角形的三边为边长向外作正方形,你能利用这个图说明勾股定理的正确性吗?你是如何做的?与同伴进行交流。
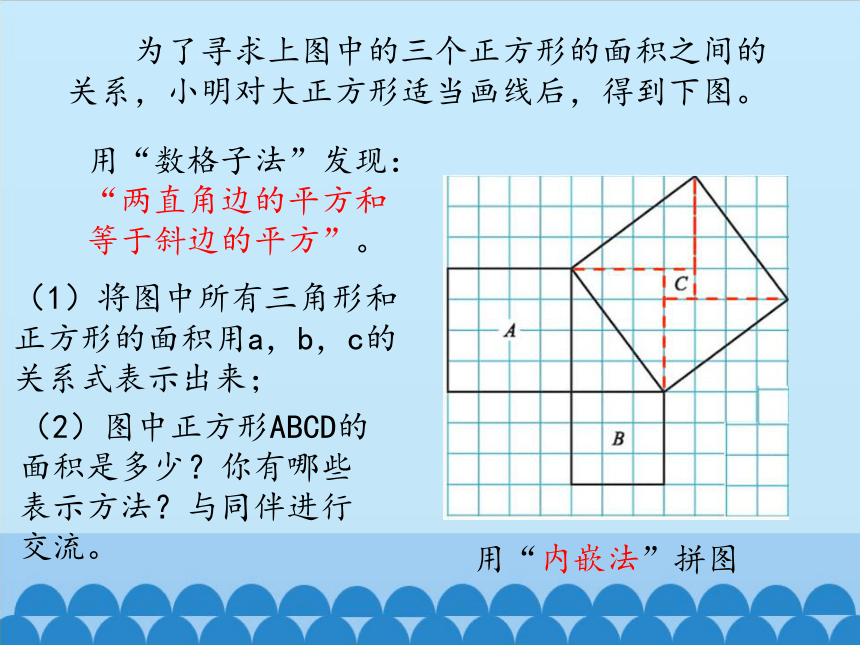
为了寻求上图中的三个正方形的面积之间的关系,小明对大正方形适当画线后,得到下图。
用“数格子法”发现:
“两直角边的平方和等于斜边的平方”。
用“内嵌法”拼图
(1)将图中所有三角形和正方形的面积用a,b,c的关系式表示出来;
(2)图中正方形ABCD的面积是多少?你有哪些表示方法?与同伴进行交流。
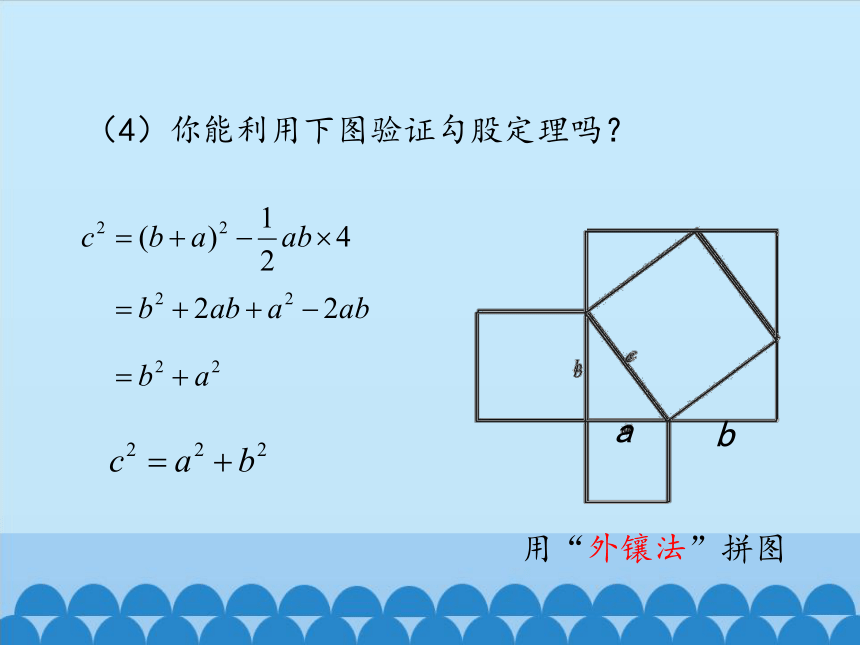
(3)你能利用下图验证勾股定理吗?
b-a
a
b
c
用“外镶法”拼图
(4)你能利用下图验证勾股定理吗?
a
b
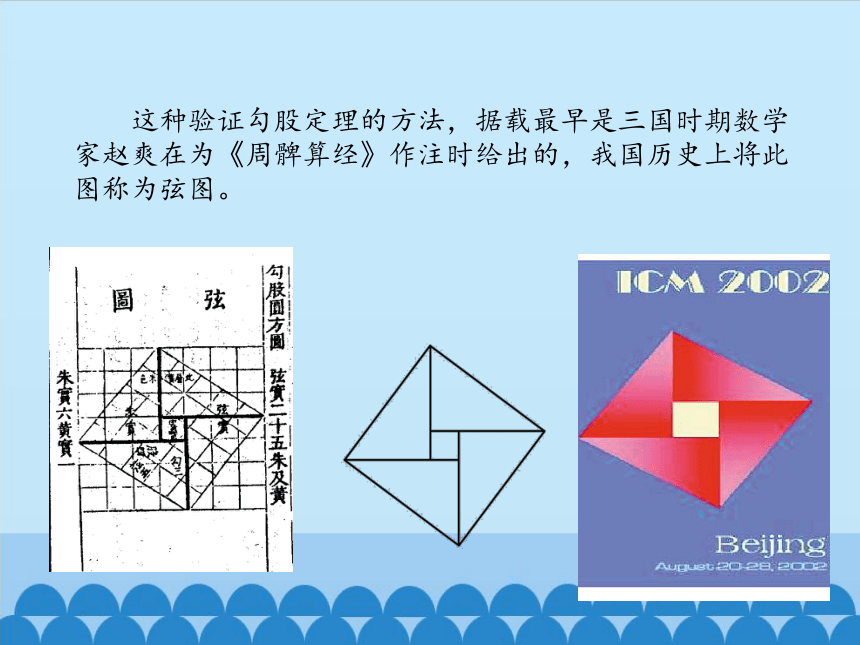
2002年的数学家大会(ICM-2002)在北京召开,这届大会会标的中央图案正是经过艺术处理的弦图,这既标志着中国古代的数学成就,又像一只转动的风车,欢迎来自世界各地的数学家们!
拓展阅读
这种验证勾股定理的方法,据载最早是三国时期数学家赵爽在为《周髀算经》作注时给出的,我国历史上将此图称为弦图。
想一想:
你还有其它的拼图方法吗?
新知归纳
“勾股定理”的验证方法:
(1)拼正方形图:
运用正方形面积表达式进行证明;
1.数形结合法:
数学理解
如图是美国总统伽菲尔德(Garfield)于1876年给出的一种验证勾股定理的办法,你能利用它验证勾股定理吗?说一说这个方法和本节的探索方法的联系。
“总统证明法”
(2)拼梯形图:
运用梯形面积表达式进行证明。
新知归纳
“勾股定理”的验证方法:
(1)拼正方形图:
运用正方形面积表达式进行证明;
1.数形结合法:
例、我方侦察员小王在距离东西向公路400米处侦察,发现一辆敌方汽车在公路上疾驶。他赶紧拿出红外测距仪,测得汽车与他相距400米,10秒后,汽车与他相距500米,你能帮助小王计算敌方汽车的速度吗?
观察图,判断图中三角形的三边长是否满足a2+b2=c2,若不满足,说出a2+b2与c2的大小关系。
1.如图,从电线杆离地面6米处向地面拉一条长
10米的缆绳,这条缆绳在地面的固定点距离电线
杆底部有多远?
已知两边求第三边
6米
10米
2.如图是某沿江地区交通图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速,已知沿江高速的建设成本是100万元/千米,该沿江高速的造价预计是多少?
3.如图,受台风“圆规”影响,一棵高18米的大树断裂,树的顶部落在离树根底部6米处,这棵树折断后有多高?
6米
x
18-x
4.如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长。
D
A
B
C
E
F
8
10
10
“勾股定理”的验证方法:
(1)拼正方形图:
运用正方形面积表达式进行证明;
(2)拼梯形图:
1.数形结合法:
运用梯形面积表达式进行证明。
谢 谢
第二课时
探索勾股定理
Contents
目录
01
02
03
04
复习旧知
巩固练习
课堂小结
新知探究
问题解决
05
勾股定理:
(1)文字语言:直角三角形两直角边的平方和等于斜边的平方。
A
B
C
a
b
c
(2)符号语言:
(已知)
(勾股定理)
上一节课,我们通过测量和数格子的方法发现了勾股定理,在图中,分别以直角三角形的三边为边长向外作正方形,你能利用这个图说明勾股定理的正确性吗?你是如何做的?与同伴进行交流。
为了寻求上图中的三个正方形的面积之间的关系,小明对大正方形适当画线后,得到下图。
用“数格子法”发现:
“两直角边的平方和等于斜边的平方”。
用“内嵌法”拼图
(1)将图中所有三角形和正方形的面积用a,b,c的关系式表示出来;
(2)图中正方形ABCD的面积是多少?你有哪些表示方法?与同伴进行交流。
(3)你能利用下图验证勾股定理吗?
b-a
a
b
c
用“外镶法”拼图
(4)你能利用下图验证勾股定理吗?
a
b
2002年的数学家大会(ICM-2002)在北京召开,这届大会会标的中央图案正是经过艺术处理的弦图,这既标志着中国古代的数学成就,又像一只转动的风车,欢迎来自世界各地的数学家们!
拓展阅读
这种验证勾股定理的方法,据载最早是三国时期数学家赵爽在为《周髀算经》作注时给出的,我国历史上将此图称为弦图。
想一想:
你还有其它的拼图方法吗?
新知归纳
“勾股定理”的验证方法:
(1)拼正方形图:
运用正方形面积表达式进行证明;
1.数形结合法:
数学理解
如图是美国总统伽菲尔德(Garfield)于1876年给出的一种验证勾股定理的办法,你能利用它验证勾股定理吗?说一说这个方法和本节的探索方法的联系。
“总统证明法”
(2)拼梯形图:
运用梯形面积表达式进行证明。
新知归纳
“勾股定理”的验证方法:
(1)拼正方形图:
运用正方形面积表达式进行证明;
1.数形结合法:
例、我方侦察员小王在距离东西向公路400米处侦察,发现一辆敌方汽车在公路上疾驶。他赶紧拿出红外测距仪,测得汽车与他相距400米,10秒后,汽车与他相距500米,你能帮助小王计算敌方汽车的速度吗?
观察图,判断图中三角形的三边长是否满足a2+b2=c2,若不满足,说出a2+b2与c2的大小关系。
1.如图,从电线杆离地面6米处向地面拉一条长
10米的缆绳,这条缆绳在地面的固定点距离电线
杆底部有多远?
已知两边求第三边
6米
10米
2.如图是某沿江地区交通图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速,已知沿江高速的建设成本是100万元/千米,该沿江高速的造价预计是多少?
3.如图,受台风“圆规”影响,一棵高18米的大树断裂,树的顶部落在离树根底部6米处,这棵树折断后有多高?
6米
x
18-x
4.如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长。
D
A
B
C
E
F
8
10
10
“勾股定理”的验证方法:
(1)拼正方形图:
运用正方形面积表达式进行证明;
(2)拼梯形图:
1.数形结合法:
运用梯形面积表达式进行证明。
谢 谢
