2021 -2022学年九年级冀教版数学上册第25章25.4相似三角形的判定 讲义
文档属性
| 名称 | 2021 -2022学年九年级冀教版数学上册第25章25.4相似三角形的判定 讲义 |
|
|
| 格式 | zip | ||
| 文件大小 | 354.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 20:59:41 | ||
图片预览





文档简介
第4讲 相似三角形的判定
教学目标
掌握相似三角形的三个判定定理
知识点梳理
知识点一 定义法判定三角形相似:三个角对应相等,三条边对应成比例的三角形相似。
如△ABC与△A'B'C'相似,记作:△ABC∽△A'B'C' ;
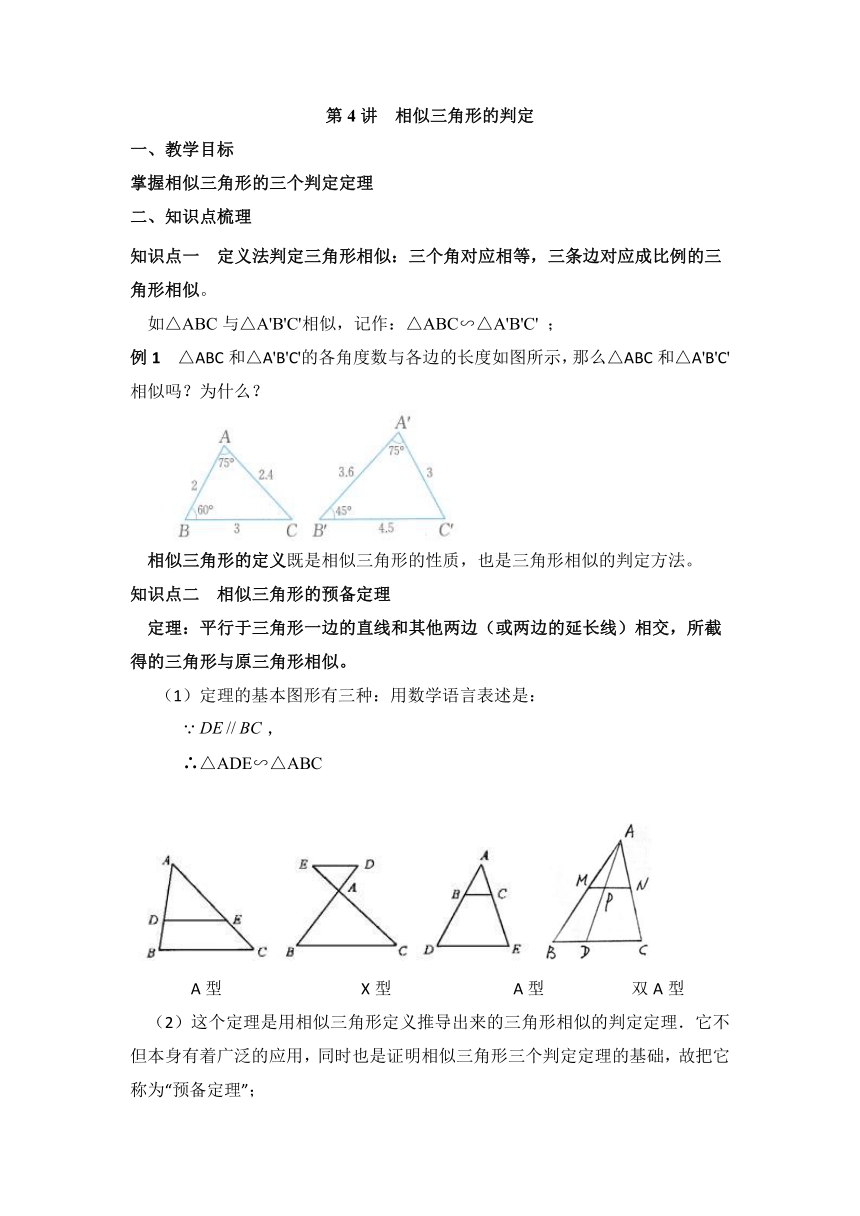
例1 △ABC和△A'B'C'的各角度数与各边的长度如图所示,那么△ABC和△A'B'C'相似吗?为什么?
相似三角形的定义既是相似三角形的性质,也是三角形相似的判定方法。
知识点二 相似三角形的预备定理
定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所截得的三角形与原三角形相似。
(1)定理的基本图形有三种:用数学语言表述是:
,
∴△ADE∽△ABC
A型 X型 A型 双A型
(2)这个定理是用相似三角形定义推导出来的三角形相似的判定定理.它不但本身有着广泛的应用,同时也是证明相似三角形三个判定定理的基础,故把它称为“预备定理”;
(3)有了预备定理后,在解题时不但要想到 “见平行,想比例”,还要想到“见平行,想相似”.
例2 如图2,在平行四边形ABCD中,过点B的直线与对角线AC、边AD分别相交于点E和F,过点E作EG∥BC,交AB于点G,则图中相似三角形有( )
A、4对 B、5对 C、6对 D、7对
图 2 图3
变式训练
2、如图3,DE∥FG∥BC,图中相似的三角形共有( )
A、4对 B、3对 C、2对 D、1对
知识点三、相似三角形的判定
判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
简述为:两角对应相等,两三角形相似.
点拨:在三角形中,若已知两个角,由三角形内角和定理可求出第三个角。
注意公共角和对顶角的运用,公共角也就是两个三角形都有的角,公共角和对顶角都是隐含的相等的角,它往往是证明相似的关键条件。
例1、如图所示,AD、BE分别是钝角三角形△ABC的边AB、AC上的高,求证:
变式训练
1已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE.
2、如图,E、F分别是△ABC的边BC上的点,DE∥AB,DF∥AC ,
求证:△ABC∽△DEF.
判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么
这两个三角形相似.
简述为:两边对应成比例且夹角相等,两三角形相似.
注意:这个角必须是两边的夹角,而不能是其他的角,其他的角则不可以识别两个三角形相似,此法类似于判定三角形全等的条件“SAS”;
例2、△ABC中,点D在AB上,如果AC2=AD AB,那么△ACD与△ABC相似吗?说说你的理由.
变式训练
3、如图,点C、D在线段AB上,△PCD是等边三角形。
(1)当AC、CD、DB满足怎样的关系时,△ACP∽△PDB?
(2)当△ACP∽△PDB时,求∠APB的度数。
判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相
似.
简述为:三边对应成比例的两三角形相似.
例3、如图在正方形网格上有A1B1C1和A2B2C2,它们相似吗?如果相似,求出相似比;如果不相似,请说明理由。
知识点四、判定直角三角形相似的方法:
(1)以上各种判定均适用.
(2)判定定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
简述为:斜边和一条直角边对应成比例,两直角三角形相似.
直角三角形被斜边上的高分成的两个直角三角形与原三角形相似.
注意:①由于直角三角形有一个角为直角,因此,在判定两个直角三角形相似时,只需再找一对对应角相等,用判定定理1,或两条直角边对应成比例,用判定定理2,一般不用判定定理3判定两个直角三角形相似;
②如图是一个十分重要的相似三角形的基本图形,图中的三角形,可称为“母子相似三角形”,其应用较为广泛.(直角三角形被斜边上的高分成的两个直三角形的与原三角形相似)
③如图,可简单记为:在Rt△ABC中,CD⊥AB,则△ABC∽△CBD∽△ACD.
④补充射影定理。
直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
公式 如图,Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下:
(1)(AD)2=BD·DC,
(2)(AB)2=BD·BC ,
(3)(AC)2=CD·BC 。
例1、已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.
求证:△ADQ∽△QCP.
变式训练
1、如上右图,AB⊥BD,CD⊥BD,P为BD上一动点,AB=60 cm,CD=40 cm,BD=140 cm,当P点在BD上由B点向D点运动时,PB的长满足什么条件,可以使图中的两个三角形相似 请说明理由。
2、已知:AD是Rt△ABC中∠A的平分线,∠C=90°,EF是AD的垂直平分线交AD于M,EF、BC的延长线交于一点N。
求证:(1)△AME∽△NMD
(2)ND2=NC·NB
知识点五:重点难点疑点突破
1、寻找相似三角形对应元素的方法与技巧
正确寻找相似三角形的对应元素是分析与解决相似三角形问题的一项基本功.通常有以下几种方法:
(1)相似三角形有公共角或对顶角时,公共角或对顶角是最明显的对应角;相似三角形中最大的角(或最小的角)一定是对应角;相似三角形中,一对相等的角是对应角,对应角所对的边是对应边,对应角的夹边是对应边;
(2)相似三角形中,一对最长的边(或最短的边)一定是对应边;对应边所对的角是对应角;对应边所夹的角是对应角.
(3)对应字母要写在对应的位置上,可直接得出对应边,对应角。
2、常见的相似三角形的基本图形:
学习三角形相似的判定,要与三角形全等的判定相比较,把证明三角形全等的思想方法迁移到相似三角形中来;对一些出现频率较高的图形,要善于归纳和记忆;对相似三角形的判定思路要善于总结,形成一整套完整的判定方法.如下表:
注:对于双垂图5有:①AB2=BD·BC;②AC2=CD·BC;③AD2=BD·CD;
对于拓展型6仅有AC2=CD·BC;
除以上6种基本图形外,常见的相似图形还有:旋转型,如下图:
(1)“平行线型”相似三角形,基本图形见前图.“见平行,想相似”是解这类题的基本思路;
(2)“相交线型”相似三角形,如上图.其中各图中都有一个公共角或对顶角.“见一对等角,找另一对等角或夹等角的两边成比例”是解这类题的基本思路;
(3)“旋转型”相似三角形,如图.若图中∠BAD=∠CAE,∠B=∠D(或∠C=∠E),则△ADE∽△ABC,该图可看成把A字型图中的△ADE绕点A旋转某一角度而形成的.
强调:
从基本图形入手能较顺利地找到解决问题的思路和方法,能帮助我们尽快地找到添加的辅助线.以上“平行线型”是常见的,这类相似三角形的对应元素有较明显的顺序,“相交线型”识图较困难,解题时要注意从复杂图形中分解或添加辅助线构造出基本图形.
例1、如图,下列每个图形中,存不存在相似的三角形,如果存在,把它们用字母表示出来,并简要说明识别的根据
2、如图,在大小为4×4的正方形方格中,△ABC的顶点A、B、C在单位正方形的顶点上,请在图中画一个△A1B1C1,使△A1B1C1∽△ABC(相似比不为1),且点A1,B1,C1都在单位正方形的顶点上.
小结:
①有平行线时,用预备定理;
②已有一对对应角相等(包括隐含的公共角或对顶角)时,可考虑利用判定定理1或判定定理2;注意公共角或对顶角或同角(等角)的余角(或补角)相等这些隐含的条件的利用;
③已有两边对应成比例时,可考虑利用判定定理2或判定定理3.但是,在选择利用判定定理2时,一对对应角相等必须是成比例两边的夹角对应相等.
特殊情况:
第一:顶角(或底角)相等的两个等腰三角形相似。
第二:腰和底对应成比例的两个等腰三角形相似。
第三:有一个锐角相等的两个直角三角形相似。
第四:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
第五:如果一个三角形的两边和其中一边上的中线与另一个三角形的两边和其中一边上的中线对应成比例,那么这两个三角形相似。
三角形相似的判定方法与全等的判定方法的联系列表如下:
类型 斜三角形 直角三角形
全等三角形的判定 SAS SSS AAS(ASA) HL
相似三角形 的判定 两边对应成比例夹角相等 三边对应成比例 两角对应相等 一条直角边与斜边对应成比例
三、典型例题
如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,△ABC和△DCE的顶点都在格点上,ED的延长线交AB于点F,
求证:(1)△ABC∽△DCE;(2)EF⊥AB
2、如图,D、E、F分别是等边△ABC三边上的点,AE=BE=CD,求证△ABC∽△DEF。
四、课堂练习
考点一、用角的关系判定三角形相似
如下图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中的相似三角形共有( )
A、1对 B、2对 C、3对 D、4对
如图,在梯形ABCD中,AD∥BC,AC与BD相交于点O,则下列三角形中,与△BOC一定相似的是( )
△ABD B、△DOA C、△ACD D、△ABO
如图,AB∥CD,AE∥FD,AE、FD分别交BC于点G、H,则图中相似三角形共有( )
A、4对 B、5对 C、6对 D、7对
如图,在△ABC中,BD、CE是高,BD与CE相交于O,则与BOE相似的三角形有( )
A、1个 B、2个 C、3个 D、4个
下列各组条件中,不能判定△ABC与△A'B'C'相似的是( )
A、∠A=∠A',∠B=∠B' B、∠C=∠C'=90°,∠A=35°,∠B'=55°
C、∠A=∠B,∠A'=∠B' D、∠A+∠B=∠A'+∠B',∠A-∠B=∠A'-∠B'
如下图,一直∠1=∠2=∠3,则下列各式正确的是( )
A、 B、 C、 D、
下列所给两个三角形不一定相似的是( )
A、两个等腰直角三角形 B、两个等边三角形
C、两个直角三角形 D、各有一个角是100°的两个等腰三角形
如下图,D、E分别在△ABC的边AB、AC上,且∠1=∠2=∠B,则图中相似三角形有( )
A、4对 B、3对 C、2对 D、1对
如下图,在△ABC中,BAC=90°,D是BC的中点,AEAD交CB的延长线于点E,下列结论正确的是( )
△AED∽△ACB B、△AEB∽△ACD
C、△BAE∽△ACE D、△AEC∽△DAC
如图,在Rt△ABC中,CD是斜边AB上的高,
求证:(1)CD2=AD·BD;(2)AC2=AD·AB.
考点二、用边角关系判定三角形相似
下列条件中,能判定△ABC和△A'B'C'相似的是( )
A、,且∠B=∠B' B、=,且∠A=∠C'
C、,且∠B=∠A' D、=,且∠A=∠B'
如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在格点为( )
A、P1 B、P2 C、P3 D、P4
如图,D是△ABC的边AB上一点,要使△ACD∽△ABC,则它们必须具备的条件是( )
A、AC:CD=AD:BC B、CD:AD=BC:AC
C、CD2=AD·DB D、AC2=AD·AB
考点三、用边的关系判定三角形相似
若△ABC和△A'B'C'满足下列条件,其中使△ABC和△A'B'C'相似的是( )
A、AB=1cm,BC=2cm,AC=2cm;A'B'=2cm,B'C'=6cm,A'C'=6cm
B、AB=2cm,BC=3cm,AC=4cm;A'B'=3cm,B'C'=6cm,A'C'=cm
C、AB=10cm,BC=AC=8cm;A'B'=cm,B'C'=A'C'=cm
D、AB=1cm,BC=cm,AC=3cm;A'B'=cm,B'C'=cm,A'C'=cm
已知△ABC的三边长分别为6cm,7.5cm,9cm,△DEF的一边长是4cm,当△DEF的另两边长是下列哪一组时,这两个三角形相似?( )
A、2cm ,3cm B、4cm,5cm C、5cm,6cm D、6cm,7cm
下列图形一定是相似的是( )
①所有三角形;②所有等边三角形;③所有等腰三角形;④所有直角三角形;⑤所有等腰直角三角形。
A、②⑤ B、①②⑤ C、②③⑤ D、②④⑤
4、如图,四个4×4的正方形网格(每个网格中的小正方形边长都是1),每个网格中均有一个“格点三角形”(三角形顶点在小正方形的顶点上),是相似三角形的是( )
A、①③ B、①② C、②③ D、②④
5、下面4×4的正方形网格,每个小正方形边均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
如图所示,若A、B、C、P、Q,甲、乙、丙、丁都是方格纸中的格点,为使△PQR∽△ABC,则点R应是甲、乙、丙、丁四点中的( )
A、甲 B、乙 C、丙 D、丁
五、课后作业:
如上右图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G;
(1)求证:△ADE≌△CFE;
(2)若GB=2,BC=4,BD=1,求AB的长;
2、已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点。
求证:△ADQ ∽△QCP
教学目标
掌握相似三角形的三个判定定理
知识点梳理
知识点一 定义法判定三角形相似:三个角对应相等,三条边对应成比例的三角形相似。
如△ABC与△A'B'C'相似,记作:△ABC∽△A'B'C' ;
例1 △ABC和△A'B'C'的各角度数与各边的长度如图所示,那么△ABC和△A'B'C'相似吗?为什么?
相似三角形的定义既是相似三角形的性质,也是三角形相似的判定方法。
知识点二 相似三角形的预备定理
定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所截得的三角形与原三角形相似。
(1)定理的基本图形有三种:用数学语言表述是:
,
∴△ADE∽△ABC
A型 X型 A型 双A型
(2)这个定理是用相似三角形定义推导出来的三角形相似的判定定理.它不但本身有着广泛的应用,同时也是证明相似三角形三个判定定理的基础,故把它称为“预备定理”;
(3)有了预备定理后,在解题时不但要想到 “见平行,想比例”,还要想到“见平行,想相似”.
例2 如图2,在平行四边形ABCD中,过点B的直线与对角线AC、边AD分别相交于点E和F,过点E作EG∥BC,交AB于点G,则图中相似三角形有( )
A、4对 B、5对 C、6对 D、7对
图 2 图3
变式训练
2、如图3,DE∥FG∥BC,图中相似的三角形共有( )
A、4对 B、3对 C、2对 D、1对
知识点三、相似三角形的判定
判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
简述为:两角对应相等,两三角形相似.
点拨:在三角形中,若已知两个角,由三角形内角和定理可求出第三个角。
注意公共角和对顶角的运用,公共角也就是两个三角形都有的角,公共角和对顶角都是隐含的相等的角,它往往是证明相似的关键条件。
例1、如图所示,AD、BE分别是钝角三角形△ABC的边AB、AC上的高,求证:
变式训练
1已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE.
2、如图,E、F分别是△ABC的边BC上的点,DE∥AB,DF∥AC ,
求证:△ABC∽△DEF.
判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么
这两个三角形相似.
简述为:两边对应成比例且夹角相等,两三角形相似.
注意:这个角必须是两边的夹角,而不能是其他的角,其他的角则不可以识别两个三角形相似,此法类似于判定三角形全等的条件“SAS”;
例2、△ABC中,点D在AB上,如果AC2=AD AB,那么△ACD与△ABC相似吗?说说你的理由.
变式训练
3、如图,点C、D在线段AB上,△PCD是等边三角形。
(1)当AC、CD、DB满足怎样的关系时,△ACP∽△PDB?
(2)当△ACP∽△PDB时,求∠APB的度数。
判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相
似.
简述为:三边对应成比例的两三角形相似.
例3、如图在正方形网格上有A1B1C1和A2B2C2,它们相似吗?如果相似,求出相似比;如果不相似,请说明理由。
知识点四、判定直角三角形相似的方法:
(1)以上各种判定均适用.
(2)判定定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
简述为:斜边和一条直角边对应成比例,两直角三角形相似.
直角三角形被斜边上的高分成的两个直角三角形与原三角形相似.
注意:①由于直角三角形有一个角为直角,因此,在判定两个直角三角形相似时,只需再找一对对应角相等,用判定定理1,或两条直角边对应成比例,用判定定理2,一般不用判定定理3判定两个直角三角形相似;
②如图是一个十分重要的相似三角形的基本图形,图中的三角形,可称为“母子相似三角形”,其应用较为广泛.(直角三角形被斜边上的高分成的两个直三角形的与原三角形相似)
③如图,可简单记为:在Rt△ABC中,CD⊥AB,则△ABC∽△CBD∽△ACD.
④补充射影定理。
直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
公式 如图,Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下:
(1)(AD)2=BD·DC,
(2)(AB)2=BD·BC ,
(3)(AC)2=CD·BC 。
例1、已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.
求证:△ADQ∽△QCP.
变式训练
1、如上右图,AB⊥BD,CD⊥BD,P为BD上一动点,AB=60 cm,CD=40 cm,BD=140 cm,当P点在BD上由B点向D点运动时,PB的长满足什么条件,可以使图中的两个三角形相似 请说明理由。
2、已知:AD是Rt△ABC中∠A的平分线,∠C=90°,EF是AD的垂直平分线交AD于M,EF、BC的延长线交于一点N。
求证:(1)△AME∽△NMD
(2)ND2=NC·NB
知识点五:重点难点疑点突破
1、寻找相似三角形对应元素的方法与技巧
正确寻找相似三角形的对应元素是分析与解决相似三角形问题的一项基本功.通常有以下几种方法:
(1)相似三角形有公共角或对顶角时,公共角或对顶角是最明显的对应角;相似三角形中最大的角(或最小的角)一定是对应角;相似三角形中,一对相等的角是对应角,对应角所对的边是对应边,对应角的夹边是对应边;
(2)相似三角形中,一对最长的边(或最短的边)一定是对应边;对应边所对的角是对应角;对应边所夹的角是对应角.
(3)对应字母要写在对应的位置上,可直接得出对应边,对应角。
2、常见的相似三角形的基本图形:
学习三角形相似的判定,要与三角形全等的判定相比较,把证明三角形全等的思想方法迁移到相似三角形中来;对一些出现频率较高的图形,要善于归纳和记忆;对相似三角形的判定思路要善于总结,形成一整套完整的判定方法.如下表:
注:对于双垂图5有:①AB2=BD·BC;②AC2=CD·BC;③AD2=BD·CD;
对于拓展型6仅有AC2=CD·BC;
除以上6种基本图形外,常见的相似图形还有:旋转型,如下图:
(1)“平行线型”相似三角形,基本图形见前图.“见平行,想相似”是解这类题的基本思路;
(2)“相交线型”相似三角形,如上图.其中各图中都有一个公共角或对顶角.“见一对等角,找另一对等角或夹等角的两边成比例”是解这类题的基本思路;
(3)“旋转型”相似三角形,如图.若图中∠BAD=∠CAE,∠B=∠D(或∠C=∠E),则△ADE∽△ABC,该图可看成把A字型图中的△ADE绕点A旋转某一角度而形成的.
强调:
从基本图形入手能较顺利地找到解决问题的思路和方法,能帮助我们尽快地找到添加的辅助线.以上“平行线型”是常见的,这类相似三角形的对应元素有较明显的顺序,“相交线型”识图较困难,解题时要注意从复杂图形中分解或添加辅助线构造出基本图形.
例1、如图,下列每个图形中,存不存在相似的三角形,如果存在,把它们用字母表示出来,并简要说明识别的根据
2、如图,在大小为4×4的正方形方格中,△ABC的顶点A、B、C在单位正方形的顶点上,请在图中画一个△A1B1C1,使△A1B1C1∽△ABC(相似比不为1),且点A1,B1,C1都在单位正方形的顶点上.
小结:
①有平行线时,用预备定理;
②已有一对对应角相等(包括隐含的公共角或对顶角)时,可考虑利用判定定理1或判定定理2;注意公共角或对顶角或同角(等角)的余角(或补角)相等这些隐含的条件的利用;
③已有两边对应成比例时,可考虑利用判定定理2或判定定理3.但是,在选择利用判定定理2时,一对对应角相等必须是成比例两边的夹角对应相等.
特殊情况:
第一:顶角(或底角)相等的两个等腰三角形相似。
第二:腰和底对应成比例的两个等腰三角形相似。
第三:有一个锐角相等的两个直角三角形相似。
第四:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
第五:如果一个三角形的两边和其中一边上的中线与另一个三角形的两边和其中一边上的中线对应成比例,那么这两个三角形相似。
三角形相似的判定方法与全等的判定方法的联系列表如下:
类型 斜三角形 直角三角形
全等三角形的判定 SAS SSS AAS(ASA) HL
相似三角形 的判定 两边对应成比例夹角相等 三边对应成比例 两角对应相等 一条直角边与斜边对应成比例
三、典型例题
如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,△ABC和△DCE的顶点都在格点上,ED的延长线交AB于点F,
求证:(1)△ABC∽△DCE;(2)EF⊥AB
2、如图,D、E、F分别是等边△ABC三边上的点,AE=BE=CD,求证△ABC∽△DEF。
四、课堂练习
考点一、用角的关系判定三角形相似
如下图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中的相似三角形共有( )
A、1对 B、2对 C、3对 D、4对
如图,在梯形ABCD中,AD∥BC,AC与BD相交于点O,则下列三角形中,与△BOC一定相似的是( )
△ABD B、△DOA C、△ACD D、△ABO
如图,AB∥CD,AE∥FD,AE、FD分别交BC于点G、H,则图中相似三角形共有( )
A、4对 B、5对 C、6对 D、7对
如图,在△ABC中,BD、CE是高,BD与CE相交于O,则与BOE相似的三角形有( )
A、1个 B、2个 C、3个 D、4个
下列各组条件中,不能判定△ABC与△A'B'C'相似的是( )
A、∠A=∠A',∠B=∠B' B、∠C=∠C'=90°,∠A=35°,∠B'=55°
C、∠A=∠B,∠A'=∠B' D、∠A+∠B=∠A'+∠B',∠A-∠B=∠A'-∠B'
如下图,一直∠1=∠2=∠3,则下列各式正确的是( )
A、 B、 C、 D、
下列所给两个三角形不一定相似的是( )
A、两个等腰直角三角形 B、两个等边三角形
C、两个直角三角形 D、各有一个角是100°的两个等腰三角形
如下图,D、E分别在△ABC的边AB、AC上,且∠1=∠2=∠B,则图中相似三角形有( )
A、4对 B、3对 C、2对 D、1对
如下图,在△ABC中,BAC=90°,D是BC的中点,AEAD交CB的延长线于点E,下列结论正确的是( )
△AED∽△ACB B、△AEB∽△ACD
C、△BAE∽△ACE D、△AEC∽△DAC
如图,在Rt△ABC中,CD是斜边AB上的高,
求证:(1)CD2=AD·BD;(2)AC2=AD·AB.
考点二、用边角关系判定三角形相似
下列条件中,能判定△ABC和△A'B'C'相似的是( )
A、,且∠B=∠B' B、=,且∠A=∠C'
C、,且∠B=∠A' D、=,且∠A=∠B'
如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在格点为( )
A、P1 B、P2 C、P3 D、P4
如图,D是△ABC的边AB上一点,要使△ACD∽△ABC,则它们必须具备的条件是( )
A、AC:CD=AD:BC B、CD:AD=BC:AC
C、CD2=AD·DB D、AC2=AD·AB
考点三、用边的关系判定三角形相似
若△ABC和△A'B'C'满足下列条件,其中使△ABC和△A'B'C'相似的是( )
A、AB=1cm,BC=2cm,AC=2cm;A'B'=2cm,B'C'=6cm,A'C'=6cm
B、AB=2cm,BC=3cm,AC=4cm;A'B'=3cm,B'C'=6cm,A'C'=cm
C、AB=10cm,BC=AC=8cm;A'B'=cm,B'C'=A'C'=cm
D、AB=1cm,BC=cm,AC=3cm;A'B'=cm,B'C'=cm,A'C'=cm
已知△ABC的三边长分别为6cm,7.5cm,9cm,△DEF的一边长是4cm,当△DEF的另两边长是下列哪一组时,这两个三角形相似?( )
A、2cm ,3cm B、4cm,5cm C、5cm,6cm D、6cm,7cm
下列图形一定是相似的是( )
①所有三角形;②所有等边三角形;③所有等腰三角形;④所有直角三角形;⑤所有等腰直角三角形。
A、②⑤ B、①②⑤ C、②③⑤ D、②④⑤
4、如图,四个4×4的正方形网格(每个网格中的小正方形边长都是1),每个网格中均有一个“格点三角形”(三角形顶点在小正方形的顶点上),是相似三角形的是( )
A、①③ B、①② C、②③ D、②④
5、下面4×4的正方形网格,每个小正方形边均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
如图所示,若A、B、C、P、Q,甲、乙、丙、丁都是方格纸中的格点,为使△PQR∽△ABC,则点R应是甲、乙、丙、丁四点中的( )
A、甲 B、乙 C、丙 D、丁
五、课后作业:
如上右图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G;
(1)求证:△ADE≌△CFE;
(2)若GB=2,BC=4,BD=1,求AB的长;
2、已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点。
求证:△ADQ ∽△QCP
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
