2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.5.1 直线与圆的位置关系 课件(29张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.5.1 直线与圆的位置关系 课件(29张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 10:50:19 | ||
图片预览







文档简介
(共29张PPT)
直线与圆的位置关系
点在圆外 d>r;
点在圆上 d=r;
点在圆内 d.A
知识回顾
点与圆的位置关系有几种?如何判断?
.C
.O
.B
设点到圆心的距离为d,圆的半径为r,则:
位置关系 数量关系
问题情景
在我们的生活中到处都蕴含着数学知识,下面请欣赏美丽的海上日出。
数学探究
直线与圆
相离
直线与圆
相切
思考分析
从海上日出这种自然现象中可以抽象出哪些基本的几何图形呢?
直线与圆的位置关系有几种 如何判断?
直线与圆
相交
规律总结
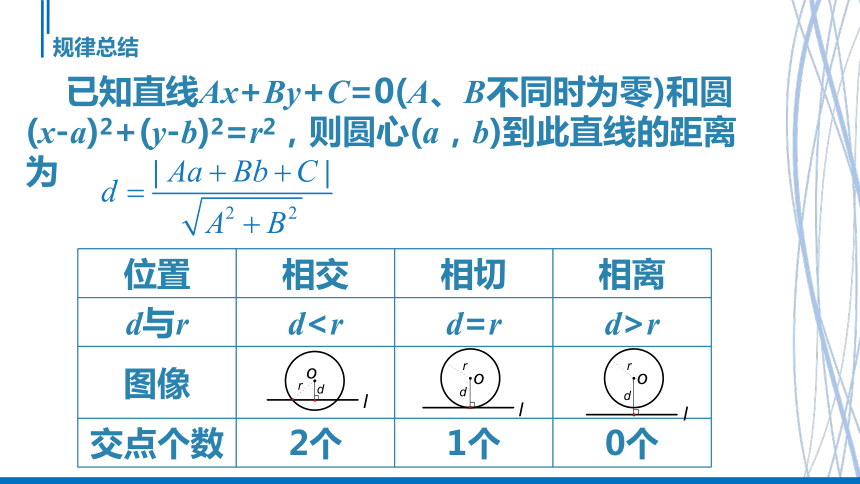
已知直线Ax+By+C=0(A、B不同时为零)和圆(x-a)2+(y-b)2=r2,则圆心(a,b)到此直线的距离为
位置 相交 相切 相离
d与r dr
图像
交点个数 2个 1个 0个
例题讲解
求直线4x+3y=40与和圆x2+y2=100的公共点坐标,并判断它们的位置关系。
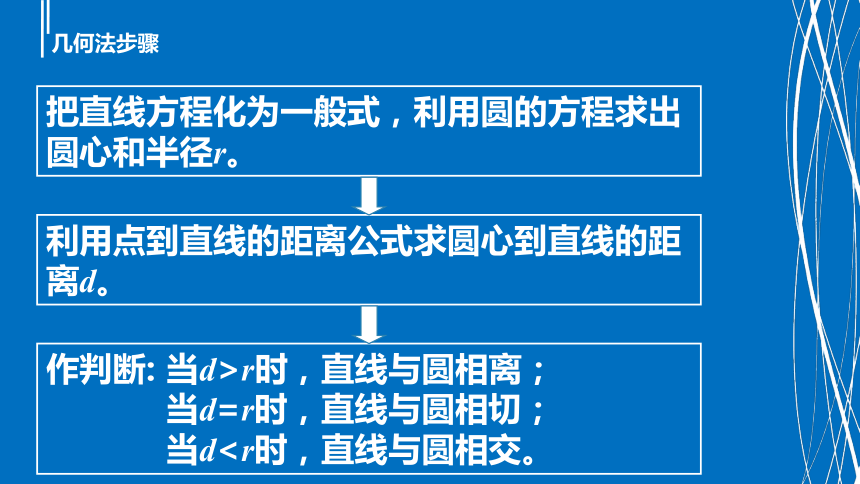
几何法步骤
利用点到直线的距离公式求圆心到直线的距离d。
作判断: 当d>r时,直线与圆相离;
当d=r时,直线与圆相切;
当d把直线方程化为一般式,利用圆的方程求出圆心和半径r。
巩固训练
3.直线x+2y-1=0和圆x2-2x+y2-y+1=0的位置关系为________
1.直线x+y-2=0与圆x2+y2=2的位置关系为________
2.直线x-y-2=0与圆(x-1)2+(y-1)2=1的位置关系为________
相交
相切
相离
巩固训练
4.已知⊙A的直径为6,点A的坐标为(-3,-4),则x轴与⊙A的位置关系是_______, y轴与⊙A的位置关系是_______。
相切
相离
O
x
y
B
C
4
3
.
A(-3,-4)
例题讲解
在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径作圆。
1、当r满足__________时,⊙C与直线AB相离。
2、当r满足__________时,⊙C与直线AB相切。
3、当r满足__________时,⊙C与直线AB相交。
0r=2.4
r>2.4
解题分析
B
C
A
D
4
5
d=2.4cm
3
由圆心到直线的距离d与半径r的大小来判断
课堂小结
1
2
判定直线与圆的位置关系的方法有______种:
在实际应用中,常采用第二种方法判定。
两
由直线与圆的公共点个数来判断
知识回顾
已知直线Ax+By+C=0(A、B不同时为零)和圆(x-a)2+(y-b)2=r2,则圆心(a,b)到此直线的距离为
位置 相交 相切 相离
d与r dr
图像
交点个数 2个 1个 0个
知识回顾
判定直线与圆的位置关系的方法
把直线方程代入圆的方程
得到一元 二次方程
求出△的值
确定圆的圆心坐标和半径r
计算圆心到直线的距离d
判断 d与圆半径r的大小关系
几何方法
代数方法
知识回顾
圆的切线性质:
切线与圆有且只有一个公共点;
圆心到切线的距离等于半径;
切线与过切点的半径垂直。
.A
.O
例题讲解
已知直线 l:x+y+C=0 和圆M:(x-1)2+(y+1)2=4, 问 C 为何值时,直线 l 与圆 M 相切?
例题讲解
1、求经过点A(-1,4)与圆M:(x-2)2+(y-3)2=1的切线l的方程。
2、求经过点A(-1,4)与圆M:x2+(y-3)2=2的切线l的方程。
注意:上述两个问题有区别吗?
变式训练
求经过点A(-1,4)与圆M:(x-2)2+(y-3)2=9的切线l的方程。
例题讲解
已知圆C的方程是x2+y2=4,求:
(1)斜率等于1的切线的方程;
(2)在y轴上的截距是 的切线方程。
课堂小结
求圆的切线方法有两种
(1)代数方法:设切线斜率,写出切线方程,联立方程,利用判别式为0;
(2)几何方法:设切线斜率,写出切线方程,用圆心到切线距离等于圆的半径.
利用斜率研究直线时,要注意直线斜率不存在的情形,应通过检验,判断它是否符合题意。
知识回顾
已知直线Ax+By+C=0(A、B不同时为零)和圆(x-a)2+(y-b)2=r2,则圆心(a,b)到此直线的距离为
位置 相交 相切 相离
d与r dr
图像
交点个数 2个 1个 0个
知识回顾
判定直线与圆的位置关系的方法
把直线方程代入圆的方程
得到一元 二次方程
求出△的值
确定圆的圆心坐标和半径r
计算圆心到直线的距离d
判断 d与圆半径r的大小关系
几何方法
代数方法
知识回顾
圆的割线性质:
切线与圆有两个公共点;
圆心与弦的中点的连线垂直于弦;
圆心与弦的中点的连线叫弦心距。
.O
.C
B.
.A
例题讲解
已知直线 l:x+y+C=0 和圆M:(x-1)2+(y+1)2=4, 问 C 为何值时,直线 l 与圆 M 相交?
例题讲解
已知直线 l:x-y+2=0被圆x2+y2=4截得的弦长。
已知过点M(-3,-3)的直线l被圆x2+y2+4y-21=0 所截得的弦长为4,求直线l的方程。
变式
训练
思考探索
设有圆(x-2)2+(y-4)2=9与直线l:ax-y+4-a=0
1)证明:无论a为何实数,直线l与圆C恒相交;
2)试求直线l被圆C截得弦长的最大值。
课堂小结
关于圆与直线相交,经常应用半径、弦心距及弦长的一半构造直角三角形,满足勾股定理:
利用斜率研究直线时,要注意直线斜率不存在的情形,应通过检验,判断它是否符合题意。
在此输入标题
输入文字
在此录入上述图表的综合分析结论
在此录入上述图表的综合分析结论
在此录入上述图表的综合分析结论
在此录入上述图表的综合分析结论
“
“
谢谢你的耐心倾听!
制作:刘海波
直线与圆的位置关系
点在圆外 d>r;
点在圆上 d=r;
点在圆内 d
知识回顾
点与圆的位置关系有几种?如何判断?
.C
.O
.B
设点到圆心的距离为d,圆的半径为r,则:
位置关系 数量关系
问题情景
在我们的生活中到处都蕴含着数学知识,下面请欣赏美丽的海上日出。
数学探究
直线与圆
相离
直线与圆
相切
思考分析
从海上日出这种自然现象中可以抽象出哪些基本的几何图形呢?
直线与圆的位置关系有几种 如何判断?
直线与圆
相交
规律总结
已知直线Ax+By+C=0(A、B不同时为零)和圆(x-a)2+(y-b)2=r2,则圆心(a,b)到此直线的距离为
位置 相交 相切 相离
d与r d
图像
交点个数 2个 1个 0个
例题讲解
求直线4x+3y=40与和圆x2+y2=100的公共点坐标,并判断它们的位置关系。
几何法步骤
利用点到直线的距离公式求圆心到直线的距离d。
作判断: 当d>r时,直线与圆相离;
当d=r时,直线与圆相切;
当d
巩固训练
3.直线x+2y-1=0和圆x2-2x+y2-y+1=0的位置关系为________
1.直线x+y-2=0与圆x2+y2=2的位置关系为________
2.直线x-y-2=0与圆(x-1)2+(y-1)2=1的位置关系为________
相交
相切
相离
巩固训练
4.已知⊙A的直径为6,点A的坐标为(-3,-4),则x轴与⊙A的位置关系是_______, y轴与⊙A的位置关系是_______。
相切
相离
O
x
y
B
C
4
3
.
A(-3,-4)
例题讲解
在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径作圆。
1、当r满足__________时,⊙C与直线AB相离。
2、当r满足__________时,⊙C与直线AB相切。
3、当r满足__________时,⊙C与直线AB相交。
0
r>2.4
解题分析
B
C
A
D
4
5
d=2.4cm
3
由圆心到直线的距离d与半径r的大小来判断
课堂小结
1
2
判定直线与圆的位置关系的方法有______种:
在实际应用中,常采用第二种方法判定。
两
由直线与圆的公共点个数来判断
知识回顾
已知直线Ax+By+C=0(A、B不同时为零)和圆(x-a)2+(y-b)2=r2,则圆心(a,b)到此直线的距离为
位置 相交 相切 相离
d与r d
图像
交点个数 2个 1个 0个
知识回顾
判定直线与圆的位置关系的方法
把直线方程代入圆的方程
得到一元 二次方程
求出△的值
确定圆的圆心坐标和半径r
计算圆心到直线的距离d
判断 d与圆半径r的大小关系
几何方法
代数方法
知识回顾
圆的切线性质:
切线与圆有且只有一个公共点;
圆心到切线的距离等于半径;
切线与过切点的半径垂直。
.A
.O
例题讲解
已知直线 l:x+y+C=0 和圆M:(x-1)2+(y+1)2=4, 问 C 为何值时,直线 l 与圆 M 相切?
例题讲解
1、求经过点A(-1,4)与圆M:(x-2)2+(y-3)2=1的切线l的方程。
2、求经过点A(-1,4)与圆M:x2+(y-3)2=2的切线l的方程。
注意:上述两个问题有区别吗?
变式训练
求经过点A(-1,4)与圆M:(x-2)2+(y-3)2=9的切线l的方程。
例题讲解
已知圆C的方程是x2+y2=4,求:
(1)斜率等于1的切线的方程;
(2)在y轴上的截距是 的切线方程。
课堂小结
求圆的切线方法有两种
(1)代数方法:设切线斜率,写出切线方程,联立方程,利用判别式为0;
(2)几何方法:设切线斜率,写出切线方程,用圆心到切线距离等于圆的半径.
利用斜率研究直线时,要注意直线斜率不存在的情形,应通过检验,判断它是否符合题意。
知识回顾
已知直线Ax+By+C=0(A、B不同时为零)和圆(x-a)2+(y-b)2=r2,则圆心(a,b)到此直线的距离为
位置 相交 相切 相离
d与r d
图像
交点个数 2个 1个 0个
知识回顾
判定直线与圆的位置关系的方法
把直线方程代入圆的方程
得到一元 二次方程
求出△的值
确定圆的圆心坐标和半径r
计算圆心到直线的距离d
判断 d与圆半径r的大小关系
几何方法
代数方法
知识回顾
圆的割线性质:
切线与圆有两个公共点;
圆心与弦的中点的连线垂直于弦;
圆心与弦的中点的连线叫弦心距。
.O
.C
B.
.A
例题讲解
已知直线 l:x+y+C=0 和圆M:(x-1)2+(y+1)2=4, 问 C 为何值时,直线 l 与圆 M 相交?
例题讲解
已知直线 l:x-y+2=0被圆x2+y2=4截得的弦长。
已知过点M(-3,-3)的直线l被圆x2+y2+4y-21=0 所截得的弦长为4,求直线l的方程。
变式
训练
思考探索
设有圆(x-2)2+(y-4)2=9与直线l:ax-y+4-a=0
1)证明:无论a为何实数,直线l与圆C恒相交;
2)试求直线l被圆C截得弦长的最大值。
课堂小结
关于圆与直线相交,经常应用半径、弦心距及弦长的一半构造直角三角形,满足勾股定理:
利用斜率研究直线时,要注意直线斜率不存在的情形,应通过检验,判断它是否符合题意。
在此输入标题
输入文字
在此录入上述图表的综合分析结论
在此录入上述图表的综合分析结论
在此录入上述图表的综合分析结论
在此录入上述图表的综合分析结论
“
“
谢谢你的耐心倾听!
制作:刘海波
