辽宁省阜新市第二高级中学2021-2022学年高二上学期期中考试数学试卷(Word版,含答案)
文档属性
| 名称 | 辽宁省阜新市第二高级中学2021-2022学年高二上学期期中考试数学试卷(Word版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 519.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 12:09:37 | ||
图片预览


文档简介
阜新市第二高级中学2021-2022学年高二上学期期中考试
数学试卷
一、选择题(每题3分,共12小题)
1.在下列选项中,能正确表示集合和关系的是( )
A. B. C.B A D.A B
2.的值为( )
A. B. C. D.
3.函数的定义域是( )
A. B. C. D.
4.已知为锐角,且,则( )
A. B. C. D.
5函数取得最小值时的自变量x等于( )
A. B. C.1 D.3
6.的值为( )
A. B. C. D.
7.两个相同的正方体骰子,六个面分别标有数字1,2,3,4,5,6,同时掷两个骰子,则两个骰子朝上面的数字之积能被6整除的概率为( )
A. B. C. D.
8.为了得到函数,的图象,只需把函数,的图象( )
A. 向右平移个单位长度 B. 向左平移个单位长度
C. 向右平移个单位长度 D. 向左平移个单位长度
9.棱长为a正四面体的表面积是 ( )
A、 B、 C、 D、
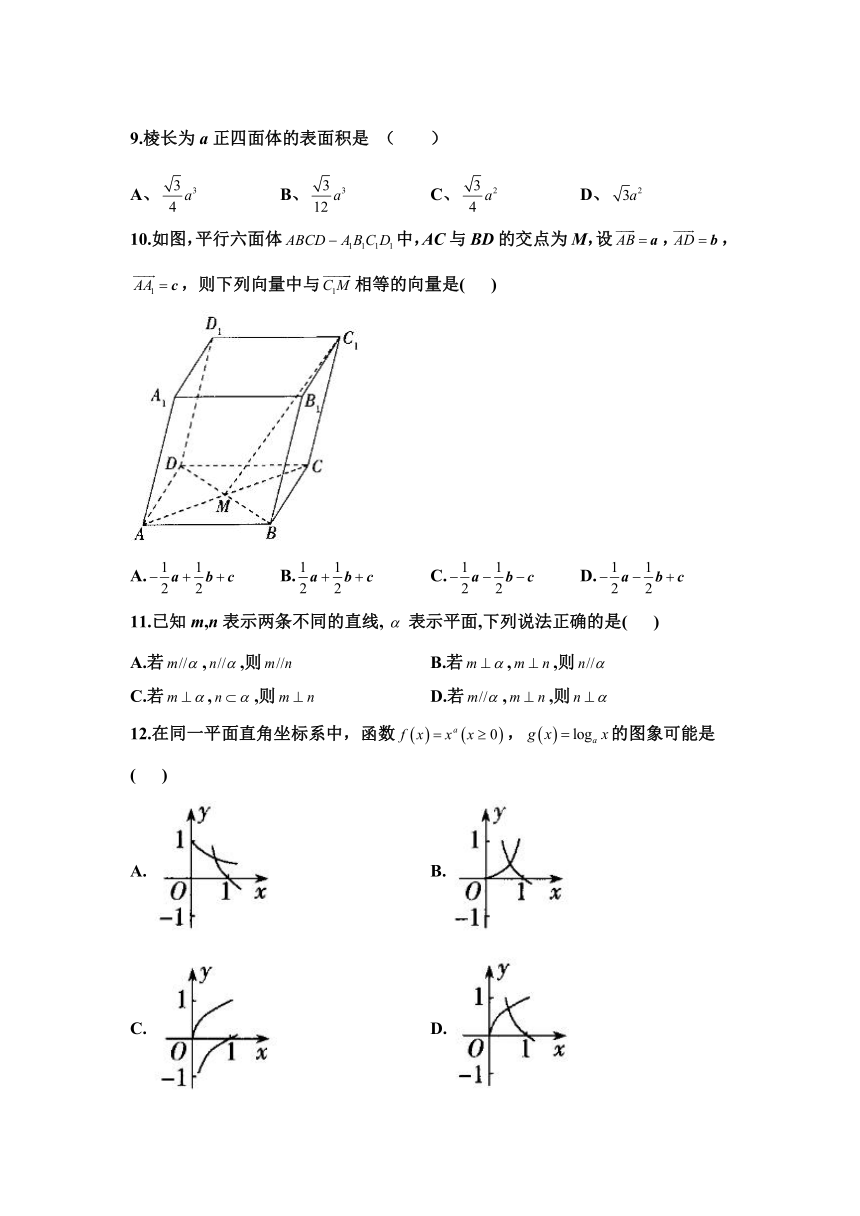
10.如图,平行六面体中,AC与BD的交点为M,设,,,则下列向量中与相等的向量是( )
A. B. C. D.
11.已知m,n表示两条不同的直线,表示平面,下列说法正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
12.在同一平面直角坐标系中,函数,的图象可能是( )
A. B.
C. D.
二、填空题(每题3分,共4小题)
13.若某中学高二年级8 个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数是_________.
14.设,则____________.
15.已知长方体的所有顶点在一个球面上,且, , 则这个球的体积为____________.
16.给出下列判断:
①一条直线和一点确定一个平面;
②两条直线确定一个平面;
③三角形和梯形一定是平面图形;
④三条互相平行的直线一定共面.
其中正确的是________________.(写出所有正确判断的序号)
三.解答题(共5小题,共52分)
17.(10分)已知向量,,求
18.(10分)如图,长方体的底面ABCD是正方形,点E在棱上,.证明:平面;
19(10分).的内角的对边分别为,已知,求的值
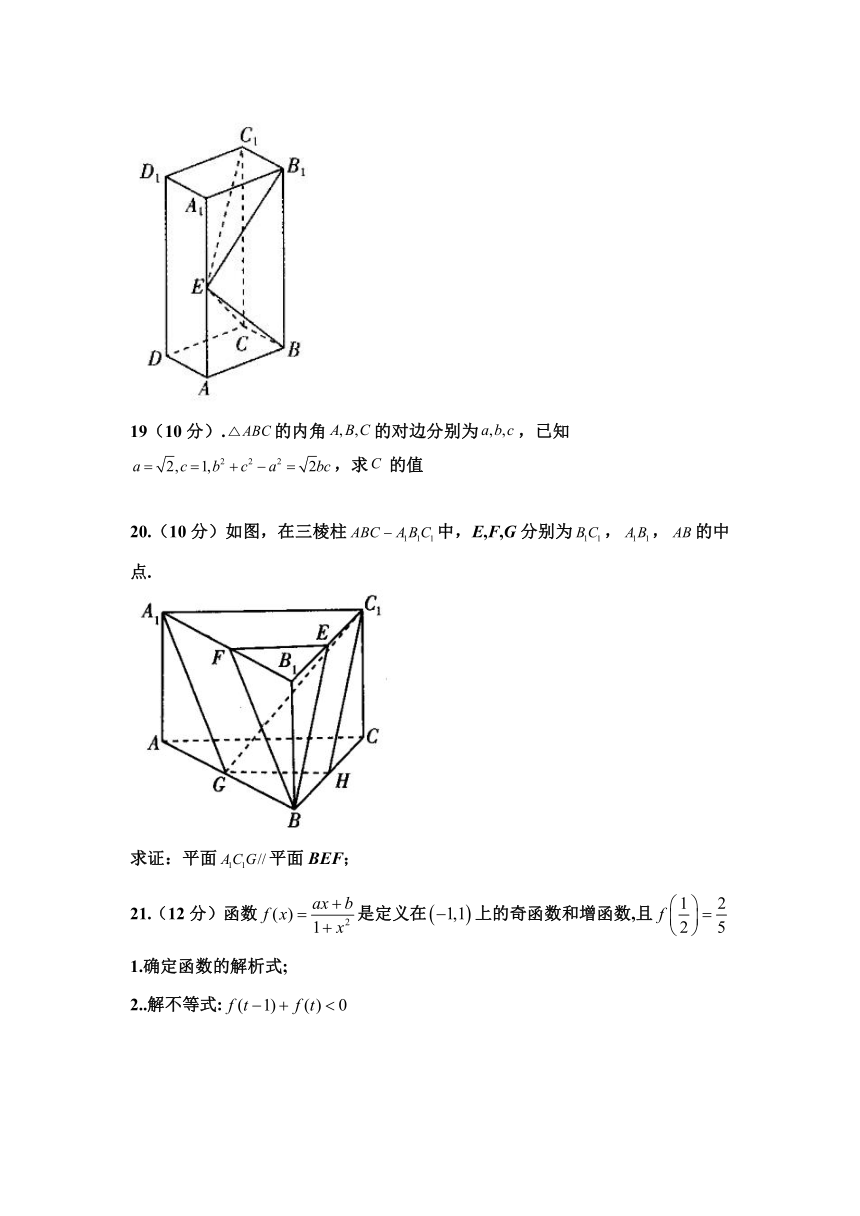
20.(10分)如图,在三棱柱中,E,F,G分别为,,的中点.
求证:平面平面BEF;
21.(12分)函数是定义在上的奇函数和增函数,且
1.确定函数的解析式;
2..解不等式:
参考答案
1.答案:C2.答案:A
3. 答案:C4.答案:B5.答案:A
6.答案:C7.答案:C8.答案:B
9.答案:D10.答案:C11.答案:C 12.答案:D
13.答案:90.5
14.答案:
15.答案:
16.答案:③
解析:一条直线与直线外一点能确定一个平面,所以①不正确;两条相交直线或两条平行直线可以确定一个平面,所以②不正确;三条互相平行的直线一定共面不正确,例如三棱柱的三条侧棱,所以④不正确;③正确.
17. 答案
18.答案:(1)【证明】由已知得平面,
平面,故.
又,所以平面.
(2)【解】由(1)知,由题设知,所以,故,.作,垂足为F,则平面,且.
所以,四棱锥的体积.
解析:
19.答案:A
解析:由于,
所以,
解得,
由于,
所以,
解得,
由于,
所以.
故选:A.
解析:
20.答案:(1)【证明】,F分别为,的中点,.
平面,平面,
平面.
又F,G分别为,AB的中点,
,,
∴四边形为平行四边形,.
平面,平面,
平面.
又,平面平面BEF.
(2)【证明】∵平面与平面ABC有公共点G,且平面,
∴平面平面.
又平面平面,平面平面,
,.
为AB的中点,为BC的中点.
解析:
21.答案:1.是上的奇函数,
,,
又,
,
2.证明:任设,且
则
,
且,又,
即
在上是增函数。
3.是奇函数,不等式可化为,
即又在上是增函数,
解得,
不等式的解集为
数学试卷
一、选择题(每题3分,共12小题)
1.在下列选项中,能正确表示集合和关系的是( )
A. B. C.B A D.A B
2.的值为( )
A. B. C. D.
3.函数的定义域是( )
A. B. C. D.
4.已知为锐角,且,则( )
A. B. C. D.
5函数取得最小值时的自变量x等于( )
A. B. C.1 D.3
6.的值为( )
A. B. C. D.
7.两个相同的正方体骰子,六个面分别标有数字1,2,3,4,5,6,同时掷两个骰子,则两个骰子朝上面的数字之积能被6整除的概率为( )
A. B. C. D.
8.为了得到函数,的图象,只需把函数,的图象( )
A. 向右平移个单位长度 B. 向左平移个单位长度
C. 向右平移个单位长度 D. 向左平移个单位长度
9.棱长为a正四面体的表面积是 ( )
A、 B、 C、 D、
10.如图,平行六面体中,AC与BD的交点为M,设,,,则下列向量中与相等的向量是( )
A. B. C. D.
11.已知m,n表示两条不同的直线,表示平面,下列说法正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
12.在同一平面直角坐标系中,函数,的图象可能是( )
A. B.
C. D.
二、填空题(每题3分,共4小题)
13.若某中学高二年级8 个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数是_________.
14.设,则____________.
15.已知长方体的所有顶点在一个球面上,且, , 则这个球的体积为____________.
16.给出下列判断:
①一条直线和一点确定一个平面;
②两条直线确定一个平面;
③三角形和梯形一定是平面图形;
④三条互相平行的直线一定共面.
其中正确的是________________.(写出所有正确判断的序号)
三.解答题(共5小题,共52分)
17.(10分)已知向量,,求
18.(10分)如图,长方体的底面ABCD是正方形,点E在棱上,.证明:平面;
19(10分).的内角的对边分别为,已知,求的值
20.(10分)如图,在三棱柱中,E,F,G分别为,,的中点.
求证:平面平面BEF;
21.(12分)函数是定义在上的奇函数和增函数,且
1.确定函数的解析式;
2..解不等式:
参考答案
1.答案:C2.答案:A
3. 答案:C4.答案:B5.答案:A
6.答案:C7.答案:C8.答案:B
9.答案:D10.答案:C11.答案:C 12.答案:D
13.答案:90.5
14.答案:
15.答案:
16.答案:③
解析:一条直线与直线外一点能确定一个平面,所以①不正确;两条相交直线或两条平行直线可以确定一个平面,所以②不正确;三条互相平行的直线一定共面不正确,例如三棱柱的三条侧棱,所以④不正确;③正确.
17. 答案
18.答案:(1)【证明】由已知得平面,
平面,故.
又,所以平面.
(2)【解】由(1)知,由题设知,所以,故,.作,垂足为F,则平面,且.
所以,四棱锥的体积.
解析:
19.答案:A
解析:由于,
所以,
解得,
由于,
所以,
解得,
由于,
所以.
故选:A.
解析:
20.答案:(1)【证明】,F分别为,的中点,.
平面,平面,
平面.
又F,G分别为,AB的中点,
,,
∴四边形为平行四边形,.
平面,平面,
平面.
又,平面平面BEF.
(2)【证明】∵平面与平面ABC有公共点G,且平面,
∴平面平面.
又平面平面,平面平面,
,.
为AB的中点,为BC的中点.
解析:
21.答案:1.是上的奇函数,
,,
又,
,
2.证明:任设,且
则
,
且,又,
即
在上是增函数。
3.是奇函数,不等式可化为,
即又在上是增函数,
解得,
不等式的解集为
同课章节目录
