2021-2022学年人教版九年级数学上册24.2.2切线的概念、切线的判定和性质 教案
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册24.2.2切线的概念、切线的判定和性质 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 169.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 06:41:58 | ||
图片预览

文档简介
切线的概念、切线的判定和性质
教学目标:1、理解切线的判定定理,并并能初步运用它解决简单的问题。
2、知道判定切线的常用的三种方法,初步掌握方法的选择。
3、掌握在解决切线的问题中常用的辅助线的作法。
情感态度:通过判定定理的学习,培养学生观察、分析和归纳问题的能力,并激发学生学习数学的兴趣;。
教学重点:切线的判定定理的理解和应用。
教学难点:理解切线判定定理的中的两个条件:一是经过半径的外端;二是直线垂直于这条半径。
教学过程:
一、创设情景,导入新课
问题:直线和圆有几种位置关系?你是如何来判断这几种位置关系的?
在学生回答后再展示相应的位置关系及判断的方法,并指明直线与圆相切是最常见与考察的内容,而判断一条直线是圆的切线,有以下方法:
1.切线的定义:与圆有唯一公共点的直线是圆的切线.
2.d与r的关系:当d=r时直线是圆的切线.
二,启发学生,探究新知
1.【例1】 已知:⊙O的半径等于3,AB=8, 并且OA=OB=5.
求证:直线AB是⊙O的切线.
老师与学生共同完成,得出证切线的方法:作垂直,证d=r.
【练一练】已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作⊙O .
求证:⊙O与AC相切.
2.教师引导:已知⊙0,以及⊙0的一条半径OA.过半径OA上一点(A除外)能作圆O的切线吗?过点A呢?
引导学生得出结论并给出几个语言:
切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
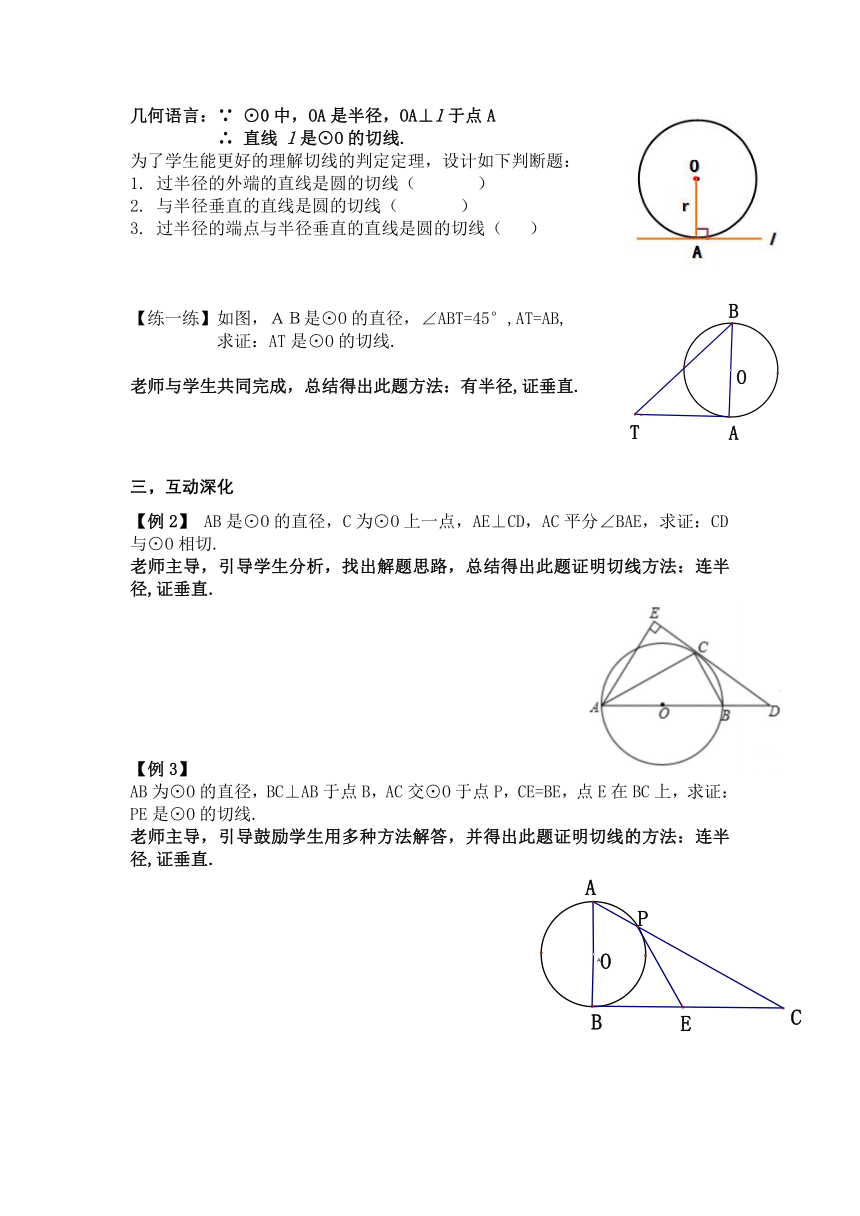
几何语言:∵ ⊙0中,OA是半径,OA⊥l于点A
∴ 直线 l是⊙O的切线.
为了学生能更好的理解切线的判定定理,设计如下判断题:
1. 过半径的外端的直线是圆的切线( )
2. 与半径垂直的直线是圆的切线( )
3. 过半径的端点与半径垂直的直线是圆的切线( )
【练一练】如图,AB是⊙O的直径,∠ABT=45°,AT=AB,
求证:AT是⊙O的切线.
老师与学生共同完成,总结得出此题方法:有半径,证垂直.
三,互动深化
【例2】 AB是⊙O的直径,C为⊙O上一点,AE⊥CD,AC平分∠BAE,求证:CD与⊙O相切.
老师主导,引导学生分析,找出解题思路,总结得出此题证明切线方法:连半径,证垂直.
【例3】
AB为⊙O的直径,BC⊥AB于点B,AC交⊙O于点P,CE=BE,点E在BC上,求证:PE是⊙O的切线.
老师主导,引导鼓励学生用多种方法解答,并得出此题证明切线的方法:连半径,证垂直.
【课堂练习】
(第2题图)
2.如图,点A,B,D在⊙O上,∠A=25°,OD的延长线交直线BC于点C,且∠OCB=40°,直线BC与⊙O 的位置关系为 .
3.已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.
4. 如图,已知⊙O的弦AB等于半径,OB并延长至C,使BC=OB.
(1) ∠ABC= 0;
(2)试判断直线AC与⊙O的位置关系,并证明你的结论.
5.如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P, PE⊥AC于E .
求证:PE是⊙O的切线.
(第3题图) (第4题图) (第5题图)
四、 课堂小结和作业
1.判断切线的方法有哪些?
(1)利用切线的定义:与圆有唯一公共点的直线是圆的切线.
(2)利用d与r的关系:当d=r时直线是圆的切线.
(3)利用切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
2. 常用的添辅助线方法?
⑴作垂直,证d=r;
⑵连半径,证垂直.
3.作业布置:
课本 P101 第1,2,4题
教学目标:1、理解切线的判定定理,并并能初步运用它解决简单的问题。
2、知道判定切线的常用的三种方法,初步掌握方法的选择。
3、掌握在解决切线的问题中常用的辅助线的作法。
情感态度:通过判定定理的学习,培养学生观察、分析和归纳问题的能力,并激发学生学习数学的兴趣;。
教学重点:切线的判定定理的理解和应用。
教学难点:理解切线判定定理的中的两个条件:一是经过半径的外端;二是直线垂直于这条半径。
教学过程:
一、创设情景,导入新课
问题:直线和圆有几种位置关系?你是如何来判断这几种位置关系的?
在学生回答后再展示相应的位置关系及判断的方法,并指明直线与圆相切是最常见与考察的内容,而判断一条直线是圆的切线,有以下方法:
1.切线的定义:与圆有唯一公共点的直线是圆的切线.
2.d与r的关系:当d=r时直线是圆的切线.
二,启发学生,探究新知
1.【例1】 已知:⊙O的半径等于3,AB=8, 并且OA=OB=5.
求证:直线AB是⊙O的切线.
老师与学生共同完成,得出证切线的方法:作垂直,证d=r.
【练一练】已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作⊙O .
求证:⊙O与AC相切.
2.教师引导:已知⊙0,以及⊙0的一条半径OA.过半径OA上一点(A除外)能作圆O的切线吗?过点A呢?
引导学生得出结论并给出几个语言:
切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
几何语言:∵ ⊙0中,OA是半径,OA⊥l于点A
∴ 直线 l是⊙O的切线.
为了学生能更好的理解切线的判定定理,设计如下判断题:
1. 过半径的外端的直线是圆的切线( )
2. 与半径垂直的直线是圆的切线( )
3. 过半径的端点与半径垂直的直线是圆的切线( )
【练一练】如图,AB是⊙O的直径,∠ABT=45°,AT=AB,
求证:AT是⊙O的切线.
老师与学生共同完成,总结得出此题方法:有半径,证垂直.
三,互动深化
【例2】 AB是⊙O的直径,C为⊙O上一点,AE⊥CD,AC平分∠BAE,求证:CD与⊙O相切.
老师主导,引导学生分析,找出解题思路,总结得出此题证明切线方法:连半径,证垂直.
【例3】
AB为⊙O的直径,BC⊥AB于点B,AC交⊙O于点P,CE=BE,点E在BC上,求证:PE是⊙O的切线.
老师主导,引导鼓励学生用多种方法解答,并得出此题证明切线的方法:连半径,证垂直.
【课堂练习】
(第2题图)
2.如图,点A,B,D在⊙O上,∠A=25°,OD的延长线交直线BC于点C,且∠OCB=40°,直线BC与⊙O 的位置关系为 .
3.已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.
4. 如图,已知⊙O的弦AB等于半径,OB并延长至C,使BC=OB.
(1) ∠ABC= 0;
(2)试判断直线AC与⊙O的位置关系,并证明你的结论.
5.如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P, PE⊥AC于E .
求证:PE是⊙O的切线.
(第3题图) (第4题图) (第5题图)
四、 课堂小结和作业
1.判断切线的方法有哪些?
(1)利用切线的定义:与圆有唯一公共点的直线是圆的切线.
(2)利用d与r的关系:当d=r时直线是圆的切线.
(3)利用切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
2. 常用的添辅助线方法?
⑴作垂直,证d=r;
⑵连半径,证垂直.
3.作业布置:
课本 P101 第1,2,4题
同课章节目录
