北师版数学七年级下册第五章 生活中的轴对称(word版含解析)
文档属性
| 名称 | 北师版数学七年级下册第五章 生活中的轴对称(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 460.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 20:23:51 | ||
图片预览

文档简介
第五章 生活中的轴对称
一、选择题(共10小题;共50分)
1. 视力表中的字母“”有各种不同的摆放方向,下面每种组合中的两个字母“”不能关于直线 成轴对称的是
A. B.
C. D.
2. 作 的平分线时,以 为圆心,某一长度为半径作弧,与 , 分别相交于 ,,然后分别以 , 为圆心,适当的长度为半径作弧,使两弧相交于一点,则这个适当的长度应
A. 大于 B. 等于 C. 小于 D. 以上都不对
3. 下列图形中,可表示塑料包装制品回收标志的是
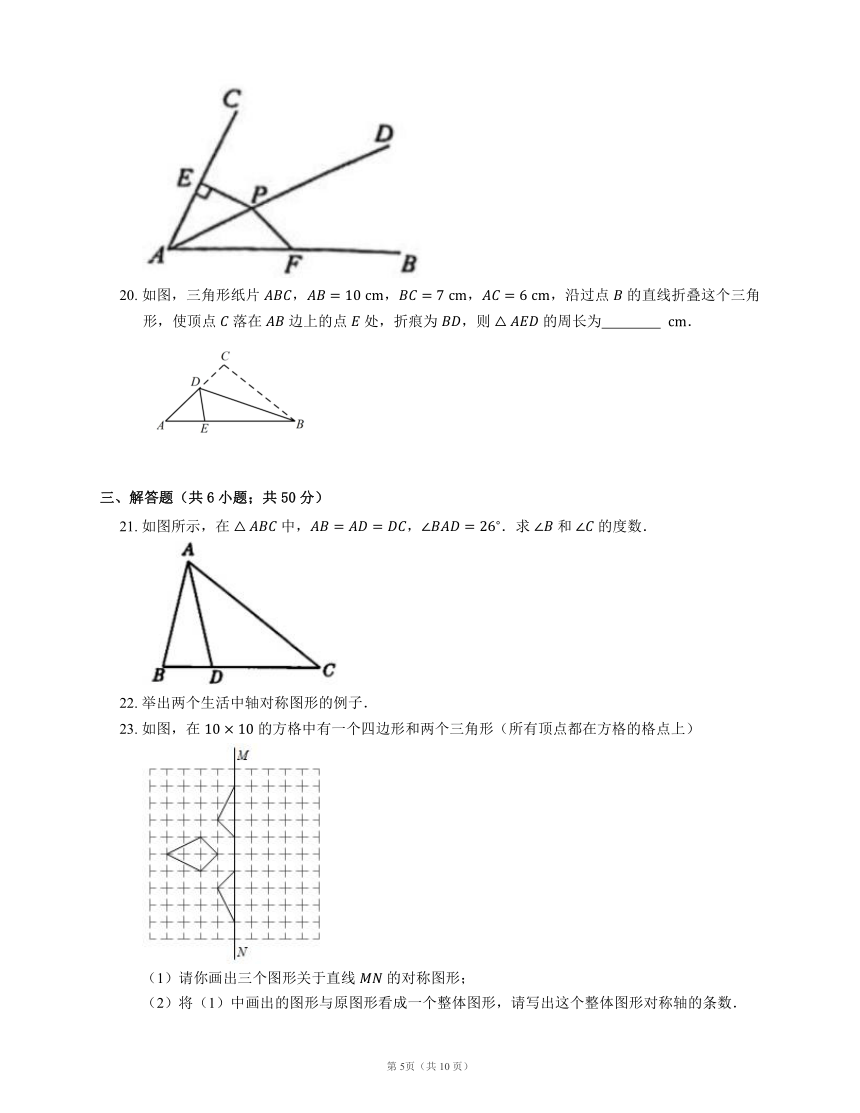
A. B.
C. D.
4. 在一些美术字中,有的汉字是轴对称图形,下面 个汉字中,可以看作是轴对称图形的是
A. B.
C. D.
5. 如图, 与 关于直线 对称,则 的度数为
A. B. C. D.
6. 等腰三角形的一个角是 ,则它的底角是
A. B. 或 C. 或 D.
7. 如图,在 中,, 平分 ,,点 到 的距离为 ,则
A. B. C. D.
8. 如图,在 中,线段 的垂直平分线与 相交于点 ,连接 ,边 的长为 ,边 的长为 ,则 的周长为
A. B. C. D.
9. 如图,正 的边长为 ,过点 的直线 ,且 与 关于直线 对称, 为线段 上一动点,则 的最小值是
A. B. C. D.
10. 对图的变化顺序描述正确的是
A. 翻折、旋转、平移 B. 翻折、平移、旋转
C. 平移、翻折、旋转 D. 旋转、翻折、平移
二、填空题(共10小题;共50分)
11. 如图,直线 是线段 的垂直平分线, 是 上的一点.如果 ,那么 .
12. 角平分线的尺规作图(如图):
()以点 为圆心,适当长为半径画弧,交 于点 ,交 于点 ;
()分别以点 为圆心,大于 的长为半径画弧,两弧在 的内部相交于点 ;
()画射线 ,射线 即为所求.
13. 下列图形:①角;②直角三角形;③等边三角形;④线段;⑤等腰三角形;⑥平行四边形.其中一定是轴对称图形的有 个.
14. 如图,在 中,.按以下步骤作图:分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于点 和点 ;作直线 交 于点 ;连接 .若 , 的周长为 ,则 的长为 .
15. 在下列字型的数字中,有两条对称轴的数字是 .
16. 在等腰三角形 中,,下列说法:
① 边上的高线和中线重合;
② 和 边上的中线的长度相等;
③ 中, 和 的平分线的长度相等;
④ 和 边上的高线的长度相等.
其中正确的是 (填序号).
17. 轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线 ,这条直线叫做 ,折叠后重合的点是对应点,叫做 .
18. 如图,在边长为 的等边三角形 中,点 ,, 分别为 ,, 的中点,点 为线段 上一个动点,连接 ,,则 周长的最小值是 .
19. 如图,点 是 的平分线 上一点, 于点 ,,有一点 在边 上运动,则 .
20. 如图,三角形纸片 ,,,,沿过点 的直线折叠这个三角形,使顶点 落在 边上的点 处,折痕为 ,则 的周长为 .
三、解答题(共6小题;共50分)
21. 如图所示,在 中,,.求 和 的度数.
22. 举出两个生活中轴对称图形的例子.
23. 如图,在 的方格中有一个四边形和两个三角形(所有顶点都在方格的格点上)
(1)请你画出三个图形关于直线 的对称图形;
(2)将(1)中画出的图形与原图形看成一个整体图形,请写出这个整体图形对称轴的条数.
24. 如图,在 的正方形格纸中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中 是一个格点三角形.
(1)请在每一个备选图中作出一个与 成轴对称的格点三角形;(不能重复)
(2)在这个 的正方形格纸中,与 成轴对称的格点三角形最多有 个.
25. 如图所示,在 , 两村之间有两条河,且每条河的宽度相同,从 村往 村,要经过两座桥 ,.现在要设计一条道路,并在两条河上分别架这两座垂直于河岸的大桥,问:如何设计这两座桥 , 的位置,使由 村到 村的路程最短 (要求在图上标出道路和大桥的位置)
26. 如图, 是 的高, 的垂直平分线分别交 , 于点 ,, 与 交于点 .求证:.
答案
第一部分
1. D
2. A
3. D 【解析】A中的图形是禁止吸烟的标志,故A不符合题意;
B中的图形是当心的警示标志,故B不符合题意;
C中的图形是节约用水的标志,故C不符合题意.
4. C
5. D
6. B
7. A 【解析】过点 作 于 ,
由题意得,,
平分 ,,,
,
,
故选:A.
8. B 【解析】 线段 的垂直平分线与 相交于点 ,
,
的周长 ,
,,
的周长 .
9. D 【解析】连接 ,如图所示:
, 均为正三角形,
,,
,
四边形 为菱形,
点 关于 对称的点是 ,即 ,
当点 与点 重合时, 取最小值,
此时 .
10. B
【解析】【分析】根据翻折、旋转、平移的定义进行判断即可.
【解析】解:由图可知,变换的顺序依次为:翻折、平移、旋转.
故选:.
【点评】本题考查了几何变换的类型,熟记各种变化的定义并准确识图是解题的关键.
第二部分
11.
12. ,,
13.
14.
15. ,,
16. ①②③
【解析】由 ,知 为底边,由等腰三角形的性质知①正确,由全等三角形的性质可判断②③正确.
17. (成轴)对称,对称轴,对称点
18.
19.
20.
【解析】由题意可得 ;
,
所以 的周长为 .
第三部分
21. ,
.
,
.
.
又 ,
.
故 ,.
22. 略.
23. (1) 所画图形如下所示:
(2) 这个整体图形共有 条对称轴.
24. (1) 与 成轴对称的格点三角形如图所示.(答案不唯一)
(2)
25. 如图所示.
()过点 作 ,垂足为 ,过点 作 ,垂足为 ;
()分别在 和 上截取 河的宽度;
()连接 ,分别交 和 于点 和 ;
()过点 和 分别作 和 的垂线段,垂足分别为 和 ;
()连接 和 ,则路线 就是满足题意的最短路线.
26. 是 的垂直平分线,
,.
在 和 中,
,
.
是 的高,
.
又 ,
,
,
.
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 视力表中的字母“”有各种不同的摆放方向,下面每种组合中的两个字母“”不能关于直线 成轴对称的是
A. B.
C. D.
2. 作 的平分线时,以 为圆心,某一长度为半径作弧,与 , 分别相交于 ,,然后分别以 , 为圆心,适当的长度为半径作弧,使两弧相交于一点,则这个适当的长度应
A. 大于 B. 等于 C. 小于 D. 以上都不对
3. 下列图形中,可表示塑料包装制品回收标志的是
A. B.
C. D.
4. 在一些美术字中,有的汉字是轴对称图形,下面 个汉字中,可以看作是轴对称图形的是
A. B.
C. D.
5. 如图, 与 关于直线 对称,则 的度数为
A. B. C. D.
6. 等腰三角形的一个角是 ,则它的底角是
A. B. 或 C. 或 D.
7. 如图,在 中,, 平分 ,,点 到 的距离为 ,则
A. B. C. D.
8. 如图,在 中,线段 的垂直平分线与 相交于点 ,连接 ,边 的长为 ,边 的长为 ,则 的周长为
A. B. C. D.
9. 如图,正 的边长为 ,过点 的直线 ,且 与 关于直线 对称, 为线段 上一动点,则 的最小值是
A. B. C. D.
10. 对图的变化顺序描述正确的是
A. 翻折、旋转、平移 B. 翻折、平移、旋转
C. 平移、翻折、旋转 D. 旋转、翻折、平移
二、填空题(共10小题;共50分)
11. 如图,直线 是线段 的垂直平分线, 是 上的一点.如果 ,那么 .
12. 角平分线的尺规作图(如图):
()以点 为圆心,适当长为半径画弧,交 于点 ,交 于点 ;
()分别以点 为圆心,大于 的长为半径画弧,两弧在 的内部相交于点 ;
()画射线 ,射线 即为所求.
13. 下列图形:①角;②直角三角形;③等边三角形;④线段;⑤等腰三角形;⑥平行四边形.其中一定是轴对称图形的有 个.
14. 如图,在 中,.按以下步骤作图:分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于点 和点 ;作直线 交 于点 ;连接 .若 , 的周长为 ,则 的长为 .
15. 在下列字型的数字中,有两条对称轴的数字是 .
16. 在等腰三角形 中,,下列说法:
① 边上的高线和中线重合;
② 和 边上的中线的长度相等;
③ 中, 和 的平分线的长度相等;
④ 和 边上的高线的长度相等.
其中正确的是 (填序号).
17. 轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线 ,这条直线叫做 ,折叠后重合的点是对应点,叫做 .
18. 如图,在边长为 的等边三角形 中,点 ,, 分别为 ,, 的中点,点 为线段 上一个动点,连接 ,,则 周长的最小值是 .
19. 如图,点 是 的平分线 上一点, 于点 ,,有一点 在边 上运动,则 .
20. 如图,三角形纸片 ,,,,沿过点 的直线折叠这个三角形,使顶点 落在 边上的点 处,折痕为 ,则 的周长为 .
三、解答题(共6小题;共50分)
21. 如图所示,在 中,,.求 和 的度数.
22. 举出两个生活中轴对称图形的例子.
23. 如图,在 的方格中有一个四边形和两个三角形(所有顶点都在方格的格点上)
(1)请你画出三个图形关于直线 的对称图形;
(2)将(1)中画出的图形与原图形看成一个整体图形,请写出这个整体图形对称轴的条数.
24. 如图,在 的正方形格纸中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中 是一个格点三角形.
(1)请在每一个备选图中作出一个与 成轴对称的格点三角形;(不能重复)
(2)在这个 的正方形格纸中,与 成轴对称的格点三角形最多有 个.
25. 如图所示,在 , 两村之间有两条河,且每条河的宽度相同,从 村往 村,要经过两座桥 ,.现在要设计一条道路,并在两条河上分别架这两座垂直于河岸的大桥,问:如何设计这两座桥 , 的位置,使由 村到 村的路程最短 (要求在图上标出道路和大桥的位置)
26. 如图, 是 的高, 的垂直平分线分别交 , 于点 ,, 与 交于点 .求证:.
答案
第一部分
1. D
2. A
3. D 【解析】A中的图形是禁止吸烟的标志,故A不符合题意;
B中的图形是当心的警示标志,故B不符合题意;
C中的图形是节约用水的标志,故C不符合题意.
4. C
5. D
6. B
7. A 【解析】过点 作 于 ,
由题意得,,
平分 ,,,
,
,
故选:A.
8. B 【解析】 线段 的垂直平分线与 相交于点 ,
,
的周长 ,
,,
的周长 .
9. D 【解析】连接 ,如图所示:
, 均为正三角形,
,,
,
四边形 为菱形,
点 关于 对称的点是 ,即 ,
当点 与点 重合时, 取最小值,
此时 .
10. B
【解析】【分析】根据翻折、旋转、平移的定义进行判断即可.
【解析】解:由图可知,变换的顺序依次为:翻折、平移、旋转.
故选:.
【点评】本题考查了几何变换的类型,熟记各种变化的定义并准确识图是解题的关键.
第二部分
11.
12. ,,
13.
14.
15. ,,
16. ①②③
【解析】由 ,知 为底边,由等腰三角形的性质知①正确,由全等三角形的性质可判断②③正确.
17. (成轴)对称,对称轴,对称点
18.
19.
20.
【解析】由题意可得 ;
,
所以 的周长为 .
第三部分
21. ,
.
,
.
.
又 ,
.
故 ,.
22. 略.
23. (1) 所画图形如下所示:
(2) 这个整体图形共有 条对称轴.
24. (1) 与 成轴对称的格点三角形如图所示.(答案不唯一)
(2)
25. 如图所示.
()过点 作 ,垂足为 ,过点 作 ,垂足为 ;
()分别在 和 上截取 河的宽度;
()连接 ,分别交 和 于点 和 ;
()过点 和 分别作 和 的垂线段,垂足分别为 和 ;
()连接 和 ,则路线 就是满足题意的最短路线.
26. 是 的垂直平分线,
,.
在 和 中,
,
.
是 的高,
.
又 ,
,
,
.
第1页(共1 页)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
