鲁教版(五四制)数学七年级上册 1.3 探索三角形全等的条件-第四课时 课件(共18张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学七年级上册 1.3 探索三角形全等的条件-第四课时 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 162.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 16:38:01 | ||
图片预览




文档简介
(共18张PPT)
探索三角形全等的条件
第四课时
1.掌握判定两个三角形全等的4种方法,并能应用它们解决简单问题。
2.学会用全等的方法证明线段(角)的相等。
3.规范解题步骤。
学习目标
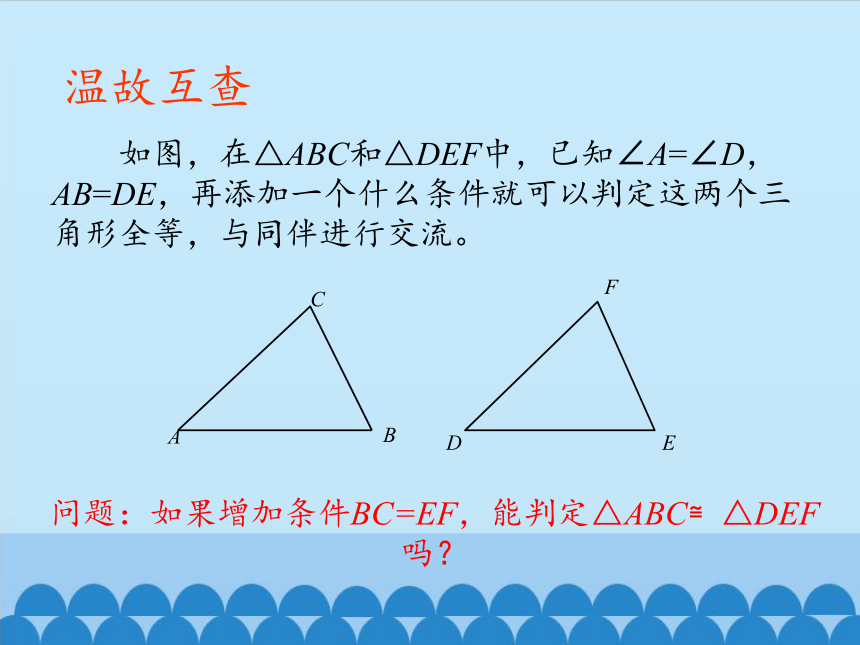
如图,在△ABC和△DEF中,已知∠A=∠D,AB=DE,再添加一个什么条件就可以判定这两个三角形全等,与同伴进行交流。
温故互查
问题:如果增加条件BC=EF,能判定△ABC≌△DEF吗?
C
A
B
D
E
F
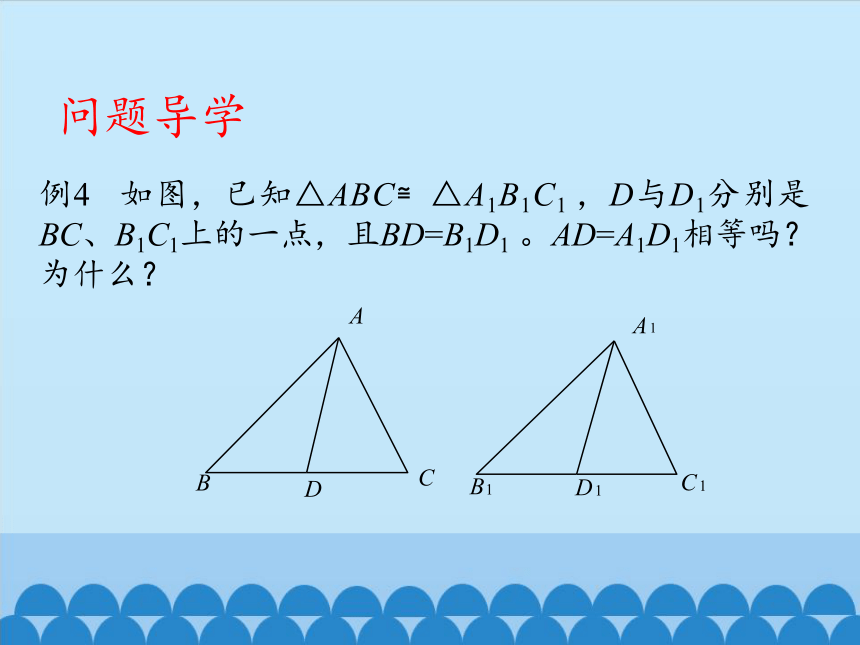
例4 如图,已知△ABC≌△A1B1C1 ,D与D1分别是BC、B1C1上的一点,且BD=B1D1 。AD=A1D1相等吗?为什么?
问题导学
A
B
D
C
A
1
B
1
D
1
C
1
证明角相等、线段相等的基本方法:证明这两个角或两条线段所在的两个三角形全等。
答:AD=A1D1
理由: ∵△ABC≌△A1B1C1
∴ ∠B=∠B1,AB=A1B1
∵在△ABD和△A1B1D1中
AB=A1B1
∠B=∠B1
BD=B1D1
∴△ABD≌△A1B1D1 (SAS)
∴ AD=A1D1
创条件
证全等
得边角
自学检测:
全等三角形对应角的平分线是否相等?对应中线和对应高呢?全等三角形的面积是否相等?
要求:先独立完成,然后小组内交流讨论,最后小组展示、点评。
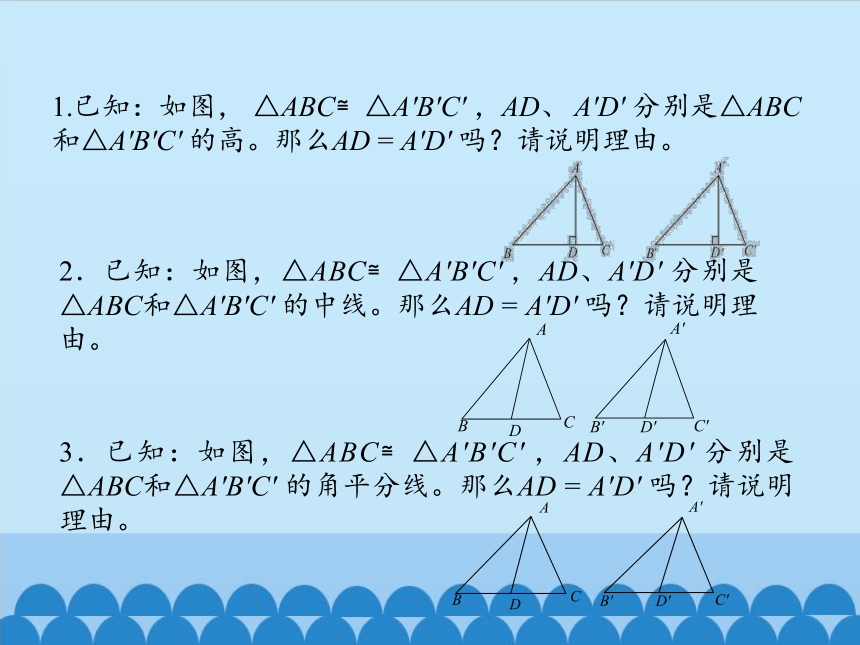
1.已知:如图, △ABC≌△A'B'C' ,AD、 A'D' 分别是△ABC和△A'B'C' 的高。那么AD = A'D' 吗?请说明理由。
2.已知:如图,△ABC≌△A'B'C' ,AD、A'D' 分别是△ABC和△A'B'C' 的中线。那么AD = A'D' 吗?请说明理由。
3.已知:如图,△ABC≌△A'B'C' ,AD、A'D' 分别是△ABC和△A'B'C' 的角平分线。那么AD = A'D' 吗?请说明理由。
A
B
C
D
A'
B'
D'
C'
A
B
C
D
A'
B'
D'
C'
A
B
C
D
A'
B'
D'
C'
A
B
C
D
A'
B'
D'
C'
答: AD=A'D'
理由: ∵△ABC≌△A'B'C'
∴ ∠B=∠B‘ ,
AB=A'B'
∵ AD 、 A'D'分别是 △ABC和 △A'B'C'的高
∴∠ADB=∠A'D'B'=90°
∴在△ABD和△A'B'D'中
∠B=∠B'
∠ADB=∠A'D'B'
AB=A'B'
∴△ABD≌△A'B'D' (AAS)
∴ AD=A'D'
( 全等三角形的对应边相等)
答: AD=A'D'
理由 :∵△ABC≌△A'B'C'
∴AB=A'B',BC=B'C',∠B=∠B'
∵AD、A'D'分别是△ABC和 △A'B'C'的中线
∴BD= BC , B'D'= B'C'
∴ BD = B'D'
∴在△ABD和△A'B'D'中
AB=A'B'
∠B=∠B'
BD=B'D'
∴△ABD≌△A'B'D' (SAS)
∴ AD=A'D'
( 全等三角形的对应边相等)
答: AD=A'D'
理由:∵△ABC≌△A'B'C'
∴AB=A'B',∠B=∠B' ,
∠BAC=∠B'A'C'
∵AD、 A'D'分别△ABC和△A'B'C'的角平分线
∴ ∠BAD= ∠BAC
∠B'A'D'= ∠B'A'C'
∴ ∠BAD =∠B'A'D'
∴在△ABD和△A'B'D'中
∠BAD =∠B'A'D'
AB=A'B'
∠B=∠B'
∴△ABD≌△A'B'D' (ASA)
∴ AD=A'D'
( 全等三角形的对应边相等)
全等三角形的对应高、对应角平分线、对应中线分别相等。
1.如图,① ∠1= ∠2② ∠3= ∠4 ③AC=AD
④BC=BD⑤ ∠C= ∠D,下面选项中能使
△ABC≌ △ABD的有( )
(A) ① ②
(B) ① ③
(C) ① ④
(D) ① ⑤
(E) ② ⑤
(F) ③ ④
ASA
SAS
AAS
×
AAS
SSS
D
A
C
B
1
2
3
4
巩固训练
2.已知:如图,AB=AD,AF=AG,BF=DG
那么 吗?为什么?
一变:图变题不变,结论还成立吗?说明理由。
A
B
F
D
G
A
B
F
D
G
再变:题变图不变,你还会证明吗?请说明理由。
已知:如图,AB=AD,AF=AG,∠BAG=∠DAF
那么BF=DG 吗?为什么?
A
B
F
D
G
A
B
F
D
G
答:∠BAG=∠DAF
理由:
∵在△ABF和△ADG中
AB=AD
AF=AG
BF=DG
∴△ABF≌△ADG(SSS)
∴∠BAF=∠DAG
∴∠BAF+ ∠FAG =
∠DAG+ ∠FAG
即:∠BAG=∠DAF
A
B
F
D
G
答:∠BAG=∠DAF
理由:
∵在△ABF和△ADG中
AB=AD
AF=AG
BF=DG
∴△ABF≌△ADG(SSS)
∴∠BAF=∠DAG
∴∠BAF-∠FAG =
∠DAG- ∠FAG
即:∠BAG=∠DAF
A
B
F
D
G
答:BF=DG
理由:∵ ∠BAG=∠DAF
∴∠BAG+ ∠FAG =
∠DAF+ ∠FAG
即:∠BAF=∠DAG
∵在△ABF和△ADG中
AB=AD
∠BAF=∠DAG
AF=AG
∴△ABF≌△ADG(SAS)
∴BF=DG
拓展延伸
1.已知:如图,AB=AD , BC=DC
那么∠B=∠D 吗?为什么?
答:∠B=∠D
理由:连接AC
∵在△ABC和△ADC中
AB=AD
BC=DC
AC=AC
∴ △ABC≌△ADC(SSS)
∴∠B=∠D
A
B
C
D
2.如图,已知AB=DC , AC=DB , 那么∠BAC=∠CDB吗?为什么?
思考:在上面的证明过程中,需要作怎样的辅助线,它的作用是什么?
答:∠BAC=∠CDB
理由:连接BC
∵在△ABC和△DCB中
AB=DC
BC=CB
AC=DB
∴ △ABC≌△DCB(SSS)
∴∠BAC=∠CDB
A
B
C
D
学习总结
今天这节课,我们有哪些收获?
1.全等三角形的对应高、对应角平分线、对应中线分别相等;
2.灵活应用4种判定方法来解决简单几何问题,体会方法的简洁性;
3.对数学转化思想的的理解与认识。
分层作业
A层:课本习题1.10 1、2
B层:课本习题1.10 3
欧几里德的几何学是人类知识史上的一座丰碑,它为人类知识的整理、系统阐述提供了一种模式。
比起欧几里德几何学中的几何知识而言,它所蕴含的方法论意义更重大。 欧氏的贡献在于用演绎法把几何学的知识贯穿起来,揭示了一个知识系统的整体结构。
后来的科学巨人麦克斯韦、牛顿、爱因斯坦等,在创建自己的科学体系时,无不是对这种方法的成功运用。
谢 谢
探索三角形全等的条件
第四课时
1.掌握判定两个三角形全等的4种方法,并能应用它们解决简单问题。
2.学会用全等的方法证明线段(角)的相等。
3.规范解题步骤。
学习目标
如图,在△ABC和△DEF中,已知∠A=∠D,AB=DE,再添加一个什么条件就可以判定这两个三角形全等,与同伴进行交流。
温故互查
问题:如果增加条件BC=EF,能判定△ABC≌△DEF吗?
C
A
B
D
E
F
例4 如图,已知△ABC≌△A1B1C1 ,D与D1分别是BC、B1C1上的一点,且BD=B1D1 。AD=A1D1相等吗?为什么?
问题导学
A
B
D
C
A
1
B
1
D
1
C
1
证明角相等、线段相等的基本方法:证明这两个角或两条线段所在的两个三角形全等。
答:AD=A1D1
理由: ∵△ABC≌△A1B1C1
∴ ∠B=∠B1,AB=A1B1
∵在△ABD和△A1B1D1中
AB=A1B1
∠B=∠B1
BD=B1D1
∴△ABD≌△A1B1D1 (SAS)
∴ AD=A1D1
创条件
证全等
得边角
自学检测:
全等三角形对应角的平分线是否相等?对应中线和对应高呢?全等三角形的面积是否相等?
要求:先独立完成,然后小组内交流讨论,最后小组展示、点评。
1.已知:如图, △ABC≌△A'B'C' ,AD、 A'D' 分别是△ABC和△A'B'C' 的高。那么AD = A'D' 吗?请说明理由。
2.已知:如图,△ABC≌△A'B'C' ,AD、A'D' 分别是△ABC和△A'B'C' 的中线。那么AD = A'D' 吗?请说明理由。
3.已知:如图,△ABC≌△A'B'C' ,AD、A'D' 分别是△ABC和△A'B'C' 的角平分线。那么AD = A'D' 吗?请说明理由。
A
B
C
D
A'
B'
D'
C'
A
B
C
D
A'
B'
D'
C'
A
B
C
D
A'
B'
D'
C'
A
B
C
D
A'
B'
D'
C'
答: AD=A'D'
理由: ∵△ABC≌△A'B'C'
∴ ∠B=∠B‘ ,
AB=A'B'
∵ AD 、 A'D'分别是 △ABC和 △A'B'C'的高
∴∠ADB=∠A'D'B'=90°
∴在△ABD和△A'B'D'中
∠B=∠B'
∠ADB=∠A'D'B'
AB=A'B'
∴△ABD≌△A'B'D' (AAS)
∴ AD=A'D'
( 全等三角形的对应边相等)
答: AD=A'D'
理由 :∵△ABC≌△A'B'C'
∴AB=A'B',BC=B'C',∠B=∠B'
∵AD、A'D'分别是△ABC和 △A'B'C'的中线
∴BD= BC , B'D'= B'C'
∴ BD = B'D'
∴在△ABD和△A'B'D'中
AB=A'B'
∠B=∠B'
BD=B'D'
∴△ABD≌△A'B'D' (SAS)
∴ AD=A'D'
( 全等三角形的对应边相等)
答: AD=A'D'
理由:∵△ABC≌△A'B'C'
∴AB=A'B',∠B=∠B' ,
∠BAC=∠B'A'C'
∵AD、 A'D'分别△ABC和△A'B'C'的角平分线
∴ ∠BAD= ∠BAC
∠B'A'D'= ∠B'A'C'
∴ ∠BAD =∠B'A'D'
∴在△ABD和△A'B'D'中
∠BAD =∠B'A'D'
AB=A'B'
∠B=∠B'
∴△ABD≌△A'B'D' (ASA)
∴ AD=A'D'
( 全等三角形的对应边相等)
全等三角形的对应高、对应角平分线、对应中线分别相等。
1.如图,① ∠1= ∠2② ∠3= ∠4 ③AC=AD
④BC=BD⑤ ∠C= ∠D,下面选项中能使
△ABC≌ △ABD的有( )
(A) ① ②
(B) ① ③
(C) ① ④
(D) ① ⑤
(E) ② ⑤
(F) ③ ④
ASA
SAS
AAS
×
AAS
SSS
D
A
C
B
1
2
3
4
巩固训练
2.已知:如图,AB=AD,AF=AG,BF=DG
那么 吗?为什么?
一变:图变题不变,结论还成立吗?说明理由。
A
B
F
D
G
A
B
F
D
G
再变:题变图不变,你还会证明吗?请说明理由。
已知:如图,AB=AD,AF=AG,∠BAG=∠DAF
那么BF=DG 吗?为什么?
A
B
F
D
G
A
B
F
D
G
答:∠BAG=∠DAF
理由:
∵在△ABF和△ADG中
AB=AD
AF=AG
BF=DG
∴△ABF≌△ADG(SSS)
∴∠BAF=∠DAG
∴∠BAF+ ∠FAG =
∠DAG+ ∠FAG
即:∠BAG=∠DAF
A
B
F
D
G
答:∠BAG=∠DAF
理由:
∵在△ABF和△ADG中
AB=AD
AF=AG
BF=DG
∴△ABF≌△ADG(SSS)
∴∠BAF=∠DAG
∴∠BAF-∠FAG =
∠DAG- ∠FAG
即:∠BAG=∠DAF
A
B
F
D
G
答:BF=DG
理由:∵ ∠BAG=∠DAF
∴∠BAG+ ∠FAG =
∠DAF+ ∠FAG
即:∠BAF=∠DAG
∵在△ABF和△ADG中
AB=AD
∠BAF=∠DAG
AF=AG
∴△ABF≌△ADG(SAS)
∴BF=DG
拓展延伸
1.已知:如图,AB=AD , BC=DC
那么∠B=∠D 吗?为什么?
答:∠B=∠D
理由:连接AC
∵在△ABC和△ADC中
AB=AD
BC=DC
AC=AC
∴ △ABC≌△ADC(SSS)
∴∠B=∠D
A
B
C
D
2.如图,已知AB=DC , AC=DB , 那么∠BAC=∠CDB吗?为什么?
思考:在上面的证明过程中,需要作怎样的辅助线,它的作用是什么?
答:∠BAC=∠CDB
理由:连接BC
∵在△ABC和△DCB中
AB=DC
BC=CB
AC=DB
∴ △ABC≌△DCB(SSS)
∴∠BAC=∠CDB
A
B
C
D
学习总结
今天这节课,我们有哪些收获?
1.全等三角形的对应高、对应角平分线、对应中线分别相等;
2.灵活应用4种判定方法来解决简单几何问题,体会方法的简洁性;
3.对数学转化思想的的理解与认识。
分层作业
A层:课本习题1.10 1、2
B层:课本习题1.10 3
欧几里德的几何学是人类知识史上的一座丰碑,它为人类知识的整理、系统阐述提供了一种模式。
比起欧几里德几何学中的几何知识而言,它所蕴含的方法论意义更重大。 欧氏的贡献在于用演绎法把几何学的知识贯穿起来,揭示了一个知识系统的整体结构。
后来的科学巨人麦克斯韦、牛顿、爱因斯坦等,在创建自己的科学体系时,无不是对这种方法的成功运用。
谢 谢
