2022年广东省普通高中学业水平合格性考试数学模拟试卷(Word含答案案解析)
文档属性
| 名称 | 2022年广东省普通高中学业水平合格性考试数学模拟试卷(Word含答案案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 482.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 00:00:00 | ||
图片预览



文档简介
2022年广东省普通高中学业水平合格性考试数学模拟试卷
考试时间:90分钟;满分:150分
第I卷(选择题)
一、单选题(每题6分,共90分)
1.设全集U=,A=,则( )
A. B. C. D.
2.下列函数中表示同一函数的是( ).
A.y=与y=() B.y=与y=
C.y= 与y=· D.y=与y=
3.计算的值为( ) A.5 B.3 C.2 D.0
4.设,,,则,,的大小关系是( )
A. B. C. D.
5.函数的零点所在区间为( )
A. B. C. D.
6.一个棱长为2的正方体,其顶点均在同一球的球面上,则该球的表面积是(参考公式:球的表面积公式为,其中R是球的半径)( )
A. B. C. D.
7..已知直线,平面,给出下列四个命题
①若,则 ②若,则 ③若 ④若
其中正确命题的个数是( ) A.0 B.1 C.2 D.3
8.已知过两点的直线与直线平行,则的值为( ).
A.-10 B.17 C.5 D.2
9.某中学有高中生3 500人,初中生1 500人,为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n的样本,已知从高中生中抽取70人,则n为( )
A.100 B.150 C.200 D.250
10.若点A(-2,-3) B(0,y) C(2,5)共线,则y的值等于( )
A.-4 B.-1 C.1 D.4
11.已知角的顶点为坐标原点,始边为x轴的正半轴,终边过点P,下列等式不正确的是( )A. B. C. D.
12.一个袋子装有四个形状、大小完全相同的球,球的编号分别为1、2、3、4,从袋中随机抽取两个球,则取出的球的编号之和等于5的概率为( )
A. B. C. D.
13.在数列{an}中,an+1=2an,a1=3,则a6=( ) A.24 B.48 C.96 D.192
14.若实数,则的最小值为( )
A. B.1 C. D.2
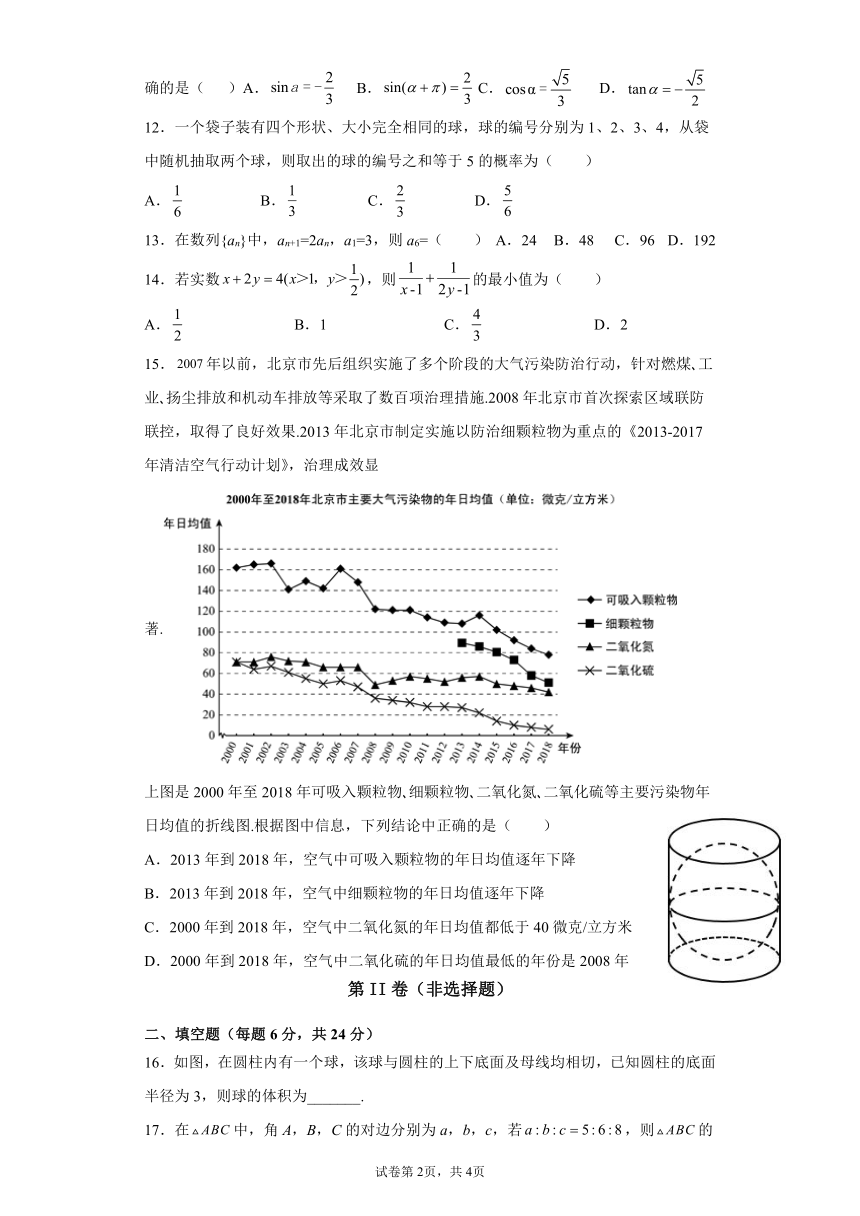
15.年以前,北京市先后组织实施了多个阶段的大气污染防治行动,针对燃煤 工业 扬尘排放和机动车排放等采取了数百项治理措施.2008年北京市首次探索区域联防联控,取得了良好效果.2013年北京市制定实施以防治细颗粒物为重点的《2013-2017年清洁空气行动计划》,治理成效显著.
上图是2000年至2018年可吸入颗粒物 细颗粒物 二氧化氮 二氧化硫等主要污染物年日均值的折线图.根据图中信息,下列结论中正确的是( )
A.2013年到2018年,空气中可吸入颗粒物的年日均值逐年下降
B.2013年到2018年,空气中细颗粒物的年日均值逐年下降
C.2000年到2018年,空气中二氧化氮的年日均值都低于40微克/立方米
D.2000年到2018年,空气中二氧化硫的年日均值最低的年份是2008年
第II卷(非选择题)
二、填空题(每题6分,共24分)
16.如图,在圆柱内有一个球,该球与圆柱的上下底面及母线均相切,已知圆柱的底面半径为3,则球的体积为_______.
17.在中,角A,B,C的对边分别为a,b,c,若,则的形状是_______三角形(填“锐角”、“钝角”、“直角”中的一个).
18.若圆心在轴上的圆经过点,且与轴相切,则圆的方程为___________.
19.两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数,按照点或小石子能排列的形状对数进行分类,如图2中的实心点个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作,第2个五角形数记作,第3个五角形数记作,第4个五角形数记作,…,若按此规律继续下去,得数列,则;对,.
三、解答题解答题(每题12分,共36分)
20.杭州市将于2022年举办第19届亚运会,本届亚运会以“绿色、智能、节位、文明”为办赛理念,展示杭州生态之美、文化之韵,充分发挥国际重大赛事对城市发展的牵引作用,从而促进经济快速发展,筹备期间,某公司带来了一种智能设备供采购商洽谈采购,并决定大量投放当地市场,已知该种设备年固定研发成本为50万元,每生产一台需另投入80元,设该公司一年内生产该设备x万台且全部售完,每万台的销售收入(万元)与年产量x(万台)满足如下关系式:
(1)写出年利润(万元)关于年产量x(万台)的函数解析式(利润=销售收入-成本)
(2)当年产量为多少万台时,该公司获得的年利润最大?并求最大利润.
21.已知为的三内角,且其对边分别为,若
(1)求; (2)若,,求的面积.
22.如图,在四棱锥中,底面ABCD是矩形,平面,分别是PB CD的中点.
(1)证明:平面PAD;
(2)若平面AEF,求四棱锥的体积.
试卷第2页,共2页
试卷第1页,共1页
答案第1页,共2页
答案第1页,共2页
2022年广东省普通高中学业水平合格性考试数学模拟试卷
参考答案
一、单选题(每题6分,共90分)
1.C 解:因为,所以
2.D
A,y=定义域为,y=()定义域为,定义域不同,不是同一函数;
B,y=定义域为,y=定义域为,定义域不同,不是同一函数;
C,y= 定义域为,y=·定义域为,
定义域不同,不是同一函数;
D,y=与y=定义域为,且y=,故两函数为同一函数.
3.C解:
4.A
解:,,,
综上可得
5.D因为均为上的增函数,
故为上的增函数,故至多有一个零点,.
而,,因为的图象不间断,
由零点存在定理可知在区间有且只有一个零点,
6.D因为正方体的对角线是其外接球的直径,
所以正方体的外接球的直径,所以,
所以该球的表面积.
7.C 分析:对①,若∥,又,所以.又,,正确;
对②,、可以平行,也可以相交,故错;
对③,若,则、有可能平行,也有可能异面,也有可能相交,故错;
对④,若∥,因为,所以.又,所以.正确.
8.D由题意结合直线平行的充要条件可得:,斜率公式有:,解得:.
9.A试题分析:根据已知可得:,故选择A
10.C由题意可知,,,
因 A(-2,-3) B(0,y) C(2,5)共线,故,即,解得,,
11.D详解:因为角的终边过点,所以,
由三角函数的定义可得:,,,而,
12.B解:从编号为1、2、3、4的4个球中随机抽取两个球,其可能结果有,,,,,共6个,其中满足编号之和等于5的有,共2个,
所以取出的球的编号之和等于5的概率
13.C因为数列{an}中,且an+1=2an,a1=3,
所以数列{an}是以3为首项,以2为公比的等比数列,所以,
14.D由条件可知,,
所以
,
当,即,结合条件 ,
可知时,等号成立,所以的最小值为.
15.B【详解】2014年空气中可吸入颗粒物年日均值比2013年多,A错;
2013年到2018年,空气中细颗粒物的年日均值逐年下降,B正确;
2007年(含2007年)之前空气中二氧化氮的年日均值都高于40微克/立方米,C错;
2000年到2018年,空气中二氧化硫的年日均值最低的年份是2018年,D错.
二、填空题(每题6分,共24分)
16.解:设球半径为,
根据题意可得:,所以球的体积.
17.钝角 设,则,显然,根据大边对大角,
因,故角为钝角,故的形状是钝角三角形.
18.
设圆心为,根据所求圆与轴相切,可得圆的方程为
又圆过点,所以有,解得 所以圆的方程为
19.
分析:因为,,,…………
所以 以上n个式子相加,得.
三、解答题解答题(每题12分,共36分)
20.【详解】
(1)由题意知:,
∴.
(2)由(1)知:,
∴时,单调递增,则;
时,,当且仅当时等号成立.
综上,当年产量为万台时,该公司获得的年利润最大为万元.
21.【详解】
解:(1)∵,
∴由正弦定理可得:,
整理得,
即:,
所以,
∵,∴,
∵,∴.
(2)由,,由余弦定理得,
∴,即有,
∴,
∴的面积为.
22.(1)证明:如图,取AP的中点为M,连接MD,ME.
因为E,M,F分别是的中点,四边形ABCD是矩形,
所以,且,所以,
∴四边形为平行四边形,∴∥,
又平面PAD,平面PAD,∴平面PAD.
(2)因为平面平面ABCD,
所以,又,所以,
因为平面平面AEF,所以,
又E是PB的中点,所以,
所以直角梯形ABCF的面积.
易知点E到平面ABCF的距离,
所以.答案第2页,共2页
答案第1页,共1页
考试时间:90分钟;满分:150分
第I卷(选择题)
一、单选题(每题6分,共90分)
1.设全集U=,A=,则( )
A. B. C. D.
2.下列函数中表示同一函数的是( ).
A.y=与y=() B.y=与y=
C.y= 与y=· D.y=与y=
3.计算的值为( ) A.5 B.3 C.2 D.0
4.设,,,则,,的大小关系是( )
A. B. C. D.
5.函数的零点所在区间为( )
A. B. C. D.
6.一个棱长为2的正方体,其顶点均在同一球的球面上,则该球的表面积是(参考公式:球的表面积公式为,其中R是球的半径)( )
A. B. C. D.
7..已知直线,平面,给出下列四个命题
①若,则 ②若,则 ③若 ④若
其中正确命题的个数是( ) A.0 B.1 C.2 D.3
8.已知过两点的直线与直线平行,则的值为( ).
A.-10 B.17 C.5 D.2
9.某中学有高中生3 500人,初中生1 500人,为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n的样本,已知从高中生中抽取70人,则n为( )
A.100 B.150 C.200 D.250
10.若点A(-2,-3) B(0,y) C(2,5)共线,则y的值等于( )
A.-4 B.-1 C.1 D.4
11.已知角的顶点为坐标原点,始边为x轴的正半轴,终边过点P,下列等式不正确的是( )A. B. C. D.
12.一个袋子装有四个形状、大小完全相同的球,球的编号分别为1、2、3、4,从袋中随机抽取两个球,则取出的球的编号之和等于5的概率为( )
A. B. C. D.
13.在数列{an}中,an+1=2an,a1=3,则a6=( ) A.24 B.48 C.96 D.192
14.若实数,则的最小值为( )
A. B.1 C. D.2
15.年以前,北京市先后组织实施了多个阶段的大气污染防治行动,针对燃煤 工业 扬尘排放和机动车排放等采取了数百项治理措施.2008年北京市首次探索区域联防联控,取得了良好效果.2013年北京市制定实施以防治细颗粒物为重点的《2013-2017年清洁空气行动计划》,治理成效显著.
上图是2000年至2018年可吸入颗粒物 细颗粒物 二氧化氮 二氧化硫等主要污染物年日均值的折线图.根据图中信息,下列结论中正确的是( )
A.2013年到2018年,空气中可吸入颗粒物的年日均值逐年下降
B.2013年到2018年,空气中细颗粒物的年日均值逐年下降
C.2000年到2018年,空气中二氧化氮的年日均值都低于40微克/立方米
D.2000年到2018年,空气中二氧化硫的年日均值最低的年份是2008年
第II卷(非选择题)
二、填空题(每题6分,共24分)
16.如图,在圆柱内有一个球,该球与圆柱的上下底面及母线均相切,已知圆柱的底面半径为3,则球的体积为_______.
17.在中,角A,B,C的对边分别为a,b,c,若,则的形状是_______三角形(填“锐角”、“钝角”、“直角”中的一个).
18.若圆心在轴上的圆经过点,且与轴相切,则圆的方程为___________.
19.两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数,按照点或小石子能排列的形状对数进行分类,如图2中的实心点个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作,第2个五角形数记作,第3个五角形数记作,第4个五角形数记作,…,若按此规律继续下去,得数列,则;对,.
三、解答题解答题(每题12分,共36分)
20.杭州市将于2022年举办第19届亚运会,本届亚运会以“绿色、智能、节位、文明”为办赛理念,展示杭州生态之美、文化之韵,充分发挥国际重大赛事对城市发展的牵引作用,从而促进经济快速发展,筹备期间,某公司带来了一种智能设备供采购商洽谈采购,并决定大量投放当地市场,已知该种设备年固定研发成本为50万元,每生产一台需另投入80元,设该公司一年内生产该设备x万台且全部售完,每万台的销售收入(万元)与年产量x(万台)满足如下关系式:
(1)写出年利润(万元)关于年产量x(万台)的函数解析式(利润=销售收入-成本)
(2)当年产量为多少万台时,该公司获得的年利润最大?并求最大利润.
21.已知为的三内角,且其对边分别为,若
(1)求; (2)若,,求的面积.
22.如图,在四棱锥中,底面ABCD是矩形,平面,分别是PB CD的中点.
(1)证明:平面PAD;
(2)若平面AEF,求四棱锥的体积.
试卷第2页,共2页
试卷第1页,共1页
答案第1页,共2页
答案第1页,共2页
2022年广东省普通高中学业水平合格性考试数学模拟试卷
参考答案
一、单选题(每题6分,共90分)
1.C 解:因为,所以
2.D
A,y=定义域为,y=()定义域为,定义域不同,不是同一函数;
B,y=定义域为,y=定义域为,定义域不同,不是同一函数;
C,y= 定义域为,y=·定义域为,
定义域不同,不是同一函数;
D,y=与y=定义域为,且y=,故两函数为同一函数.
3.C解:
4.A
解:,,,
综上可得
5.D因为均为上的增函数,
故为上的增函数,故至多有一个零点,.
而,,因为的图象不间断,
由零点存在定理可知在区间有且只有一个零点,
6.D因为正方体的对角线是其外接球的直径,
所以正方体的外接球的直径,所以,
所以该球的表面积.
7.C 分析:对①,若∥,又,所以.又,,正确;
对②,、可以平行,也可以相交,故错;
对③,若,则、有可能平行,也有可能异面,也有可能相交,故错;
对④,若∥,因为,所以.又,所以.正确.
8.D由题意结合直线平行的充要条件可得:,斜率公式有:,解得:.
9.A试题分析:根据已知可得:,故选择A
10.C由题意可知,,,
因 A(-2,-3) B(0,y) C(2,5)共线,故,即,解得,,
11.D详解:因为角的终边过点,所以,
由三角函数的定义可得:,,,而,
12.B解:从编号为1、2、3、4的4个球中随机抽取两个球,其可能结果有,,,,,共6个,其中满足编号之和等于5的有,共2个,
所以取出的球的编号之和等于5的概率
13.C因为数列{an}中,且an+1=2an,a1=3,
所以数列{an}是以3为首项,以2为公比的等比数列,所以,
14.D由条件可知,,
所以
,
当,即,结合条件 ,
可知时,等号成立,所以的最小值为.
15.B【详解】2014年空气中可吸入颗粒物年日均值比2013年多,A错;
2013年到2018年,空气中细颗粒物的年日均值逐年下降,B正确;
2007年(含2007年)之前空气中二氧化氮的年日均值都高于40微克/立方米,C错;
2000年到2018年,空气中二氧化硫的年日均值最低的年份是2018年,D错.
二、填空题(每题6分,共24分)
16.解:设球半径为,
根据题意可得:,所以球的体积.
17.钝角 设,则,显然,根据大边对大角,
因,故角为钝角,故的形状是钝角三角形.
18.
设圆心为,根据所求圆与轴相切,可得圆的方程为
又圆过点,所以有,解得 所以圆的方程为
19.
分析:因为,,,…………
所以 以上n个式子相加,得.
三、解答题解答题(每题12分,共36分)
20.【详解】
(1)由题意知:,
∴.
(2)由(1)知:,
∴时,单调递增,则;
时,,当且仅当时等号成立.
综上,当年产量为万台时,该公司获得的年利润最大为万元.
21.【详解】
解:(1)∵,
∴由正弦定理可得:,
整理得,
即:,
所以,
∵,∴,
∵,∴.
(2)由,,由余弦定理得,
∴,即有,
∴,
∴的面积为.
22.(1)证明:如图,取AP的中点为M,连接MD,ME.
因为E,M,F分别是的中点,四边形ABCD是矩形,
所以,且,所以,
∴四边形为平行四边形,∴∥,
又平面PAD,平面PAD,∴平面PAD.
(2)因为平面平面ABCD,
所以,又,所以,
因为平面平面AEF,所以,
又E是PB的中点,所以,
所以直角梯形ABCF的面积.
易知点E到平面ABCF的距离,
所以.答案第2页,共2页
答案第1页,共1页
同课章节目录
