鲁教版(五四制)数学七年级上册 3.3 勾股定理的应用举例-第一课时 课件 (共19张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学七年级上册 3.3 勾股定理的应用举例-第一课时 课件 (共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 361.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 17:35:43 | ||
图片预览






文档简介
(共19张PPT)
第一课时
勾股定理的应用举例
Contents
目录
01
02
03
04
诊断练习
巩固练习
课堂小结
例题讲解
05
问题情境一
06
问题情境二
1.圆柱的底面半径为3cm,高为12cm,求圆柱的侧面积。
A
A'
C'
C
12
6π
S侧=72π(cm2)
3
12
A
C
2.如图(1)是一个正方体,下面哪个不是正方体的展开图( )
图(1)
A
B
C
D
1.如图,有一个圆柱,它的高等于12cm,底面圆的周长为18cm,在圆柱下底面的A点有一只蚂蚁,它想吃到地面上与A点相对的B点处的食物,沿圆柱侧面爬行的最短路程是多少?
(1)在你自己做的圆柱上,尝试从点A到点B沿圆柱侧面画几条路线,你觉得哪条路线最短?
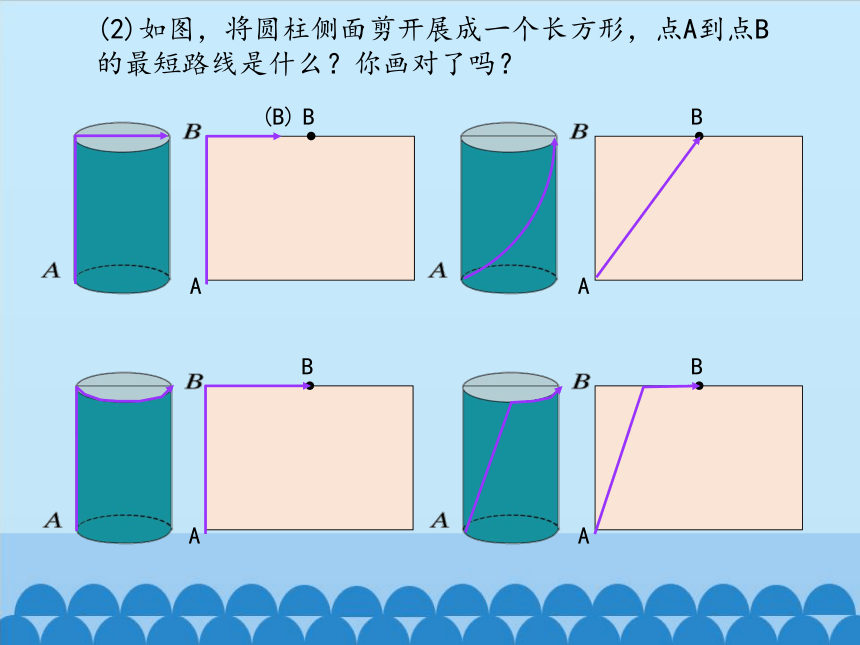
(2)如图,将圆柱侧面剪开展成一个长方形,点A到点B的最短路线是什么?你画对了吗?
A
B
(B)
A
B
A
B
A
B
(3)蚂蚁从点A出发,想吃到B点上的食物,它沿
圆柱侧面爬行的最短路程是多少?
12厘米
9厘米
AB2=122+92
AB=15(厘米)
(4)若蚂蚁先从点A直接向上爬到点C,然后再从点C沿底面直径爬到点B,这样爬的总路程与沿圆柱侧面爬行的最短路程比较,哪一条更短些?
12厘米
9厘米
AC+BC=12+9=21(厘米)
AB=15(厘米)
C
C
AB新知归纳
数学思想:
立体图形
平面图形
转化
展开
(1)
2.李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺。
(1)你能替他想办法完成任务吗?
连接对角线AC,只要分别量出
AB、BC、AC的长度即可。
若:AB2+BC2=AC2
△ABC为直角三角形
同理可证△ABD为直角三角形
2.李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺。
(2)李叔叔量得AD长是30cm,AB长是40cm,BD长是50cm。AD边垂直于AB边吗?
经计算AD2+AB2=BD2
AD⊥AB
2.李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺。
(3)小明随身只有一个长度为20cm的刻度尺,他能有办法检验AD边是否垂直于AB边吗?BC边与AB边呢?
新知归纳
数学思想:
实际问题
数学问题
转化
建模
(2)
1.甲、乙两位探险者到沙漠进行探险。某日早晨8︰00甲先出发,他以6km/h的速度向正东行走。1h后乙出发,他以5km/h的速度向正北行走。上午10︰00,甲、乙二人相距多远?
A
C
B
5km
12km
2.如图,带阴影的矩形面积是多少?
17厘米
S=17×3=51厘米2
3.一个无盖的长方形盒子的长、宽、高分别是8cm,8cm,12cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,你能帮蚂蚁设计一条最短的路线吗?蚂蚁要爬行的最短行程是多少?
8
12
8
A
B
A
B
8
8
12
数学思想:
立体图形
平面图形
转化
展开
(1)
实际问题
数学问题
转化
建模
(2)
谢 谢
第一课时
勾股定理的应用举例
Contents
目录
01
02
03
04
诊断练习
巩固练习
课堂小结
例题讲解
05
问题情境一
06
问题情境二
1.圆柱的底面半径为3cm,高为12cm,求圆柱的侧面积。
A
A'
C'
C
12
6π
S侧=72π(cm2)
3
12
A
C
2.如图(1)是一个正方体,下面哪个不是正方体的展开图( )
图(1)
A
B
C
D
1.如图,有一个圆柱,它的高等于12cm,底面圆的周长为18cm,在圆柱下底面的A点有一只蚂蚁,它想吃到地面上与A点相对的B点处的食物,沿圆柱侧面爬行的最短路程是多少?
(1)在你自己做的圆柱上,尝试从点A到点B沿圆柱侧面画几条路线,你觉得哪条路线最短?
(2)如图,将圆柱侧面剪开展成一个长方形,点A到点B的最短路线是什么?你画对了吗?
A
B
(B)
A
B
A
B
A
B
(3)蚂蚁从点A出发,想吃到B点上的食物,它沿
圆柱侧面爬行的最短路程是多少?
12厘米
9厘米
AB2=122+92
AB=15(厘米)
(4)若蚂蚁先从点A直接向上爬到点C,然后再从点C沿底面直径爬到点B,这样爬的总路程与沿圆柱侧面爬行的最短路程比较,哪一条更短些?
12厘米
9厘米
AC+BC=12+9=21(厘米)
AB=15(厘米)
C
C
AB
数学思想:
立体图形
平面图形
转化
展开
(1)
2.李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺。
(1)你能替他想办法完成任务吗?
连接对角线AC,只要分别量出
AB、BC、AC的长度即可。
若:AB2+BC2=AC2
△ABC为直角三角形
同理可证△ABD为直角三角形
2.李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺。
(2)李叔叔量得AD长是30cm,AB长是40cm,BD长是50cm。AD边垂直于AB边吗?
经计算AD2+AB2=BD2
AD⊥AB
2.李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺。
(3)小明随身只有一个长度为20cm的刻度尺,他能有办法检验AD边是否垂直于AB边吗?BC边与AB边呢?
新知归纳
数学思想:
实际问题
数学问题
转化
建模
(2)
1.甲、乙两位探险者到沙漠进行探险。某日早晨8︰00甲先出发,他以6km/h的速度向正东行走。1h后乙出发,他以5km/h的速度向正北行走。上午10︰00,甲、乙二人相距多远?
A
C
B
5km
12km
2.如图,带阴影的矩形面积是多少?
17厘米
S=17×3=51厘米2
3.一个无盖的长方形盒子的长、宽、高分别是8cm,8cm,12cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,你能帮蚂蚁设计一条最短的路线吗?蚂蚁要爬行的最短行程是多少?
8
12
8
A
B
A
B
8
8
12
数学思想:
立体图形
平面图形
转化
展开
(1)
实际问题
数学问题
转化
建模
(2)
谢 谢
