鲁教版(五四制)数学七年级上册 3.3 勾股定理的应用举例(1) 课件(共15张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学七年级上册 3.3 勾股定理的应用举例(1) 课件(共15张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 514.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
鲁教版七年级上册第三章第三节
出示问题:
1.从综合楼A点走到
教学楼B点怎样走最近?
2.其理由是什么?
两点之间,线段最短
情景引入
例 如图所示,有一个圆柱,它的高是12cm,底面上圆的周长等于18cm,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行到B点,求其爬行的最短路程是多少?
【探究点】如何确定圆柱体侧面两点间的最短路线
探究新知
1.能利用勾股定理灵活地求出一些圆柱表面距
离的最小值问题,进一步发展学生的应用意
识.
2.经历将实际问题抽象成数学问题解决的过
程,提高学生的观察能力、动手操作能力、
分析解决问题的能力及合作交流的能力.
教学目标
[活动要求]:
请同学们拿出已做好的圆柱
1.在图上标出点A、点B的位置
2.尝试着从点A到点B沿圆柱侧面进行比划,寻找
蚂蚁爬行的所有路径情况。
例 如图所示,有一个圆柱,它的高是12cm,
底面上圆的周长等于18cm,在圆柱下底面的
点A处有一只蚂蚁,它想吃到上底面上与点A
相对的点B处的食物,沿圆柱侧面爬行到B点,
求其爬行的最短路程是多少?
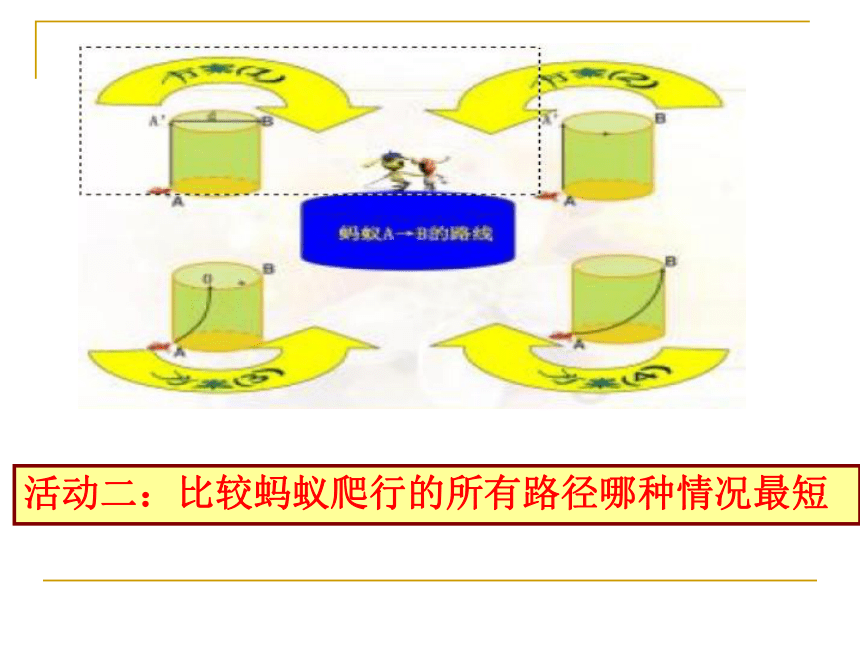
活动一:找出蚂蚁爬行的所有路径的情况
活动二:比较蚂蚁爬行的所有路径哪种情况最短
[活动步骤]:
1.明确圆柱的侧面展开图是什么?
[活动要求]:
沿着点A或点B所在的一条母线将圆柱剪开,观察定位点A、点B的位置,并画出示意图。
3.操作验证
2.猜想点A、点B在侧面展开图中的位置。
活动三:寻求蚂蚁爬行的所有路径中最短路径的求法
反思:求最短路径的方法是什么?
展成平面图形
确定最短路线(即两个点的具体位置)
确定直角三角形
利用勾股定理求解
B
C
A
求最短路径的方法
反思:解决这一类几何型问题的步骤是什么?
解决实际问题的关键是根据实际问题建立相应的数学模型,解决这一类几何型问题的具体步骤大致可以归纳如下:
1.审题——分析实际问题;
2.建模——建立相应的数学模型;
3.求解——运用勾股定理计算;
4.检验——是否符合实际问题的真实性.
反思:解决本题目的关键是什么?
方法提炼
[变式1].
如图,有一圆柱,其高为8cm,它的底面周长为16cm,在圆柱外侧距下底1cm的A处有一只蚂蚁,它想得到距上底1cm 的B处的食物,则蚂蚁经过的最短路程是多少?
小试牛刀
[变式2].
有一圆柱形油罐如图所示,已知油罐的底面圆半径是2米,高为5米,要从A点起环绕油罐建梯子,梯子的顶端正好到达A点的正上方B点,则梯子最少需要多少米(∏=3).
小试牛刀
[变式3].
我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是 多少 尺?
小试牛刀
如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为多少 m(容器厚度忽略不计).
思维加油站
1.本节课你学习了哪些知识?有哪些收获?体
现了什么数学思想?
2. 请填写学习评价表:你本节课的表现( )
A.优秀 B.良好 C.合格
盘点收获
谢谢大家
再见
鲁教版七年级上册第三章第三节
出示问题:
1.从综合楼A点走到
教学楼B点怎样走最近?
2.其理由是什么?
两点之间,线段最短
情景引入
例 如图所示,有一个圆柱,它的高是12cm,底面上圆的周长等于18cm,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行到B点,求其爬行的最短路程是多少?
【探究点】如何确定圆柱体侧面两点间的最短路线
探究新知
1.能利用勾股定理灵活地求出一些圆柱表面距
离的最小值问题,进一步发展学生的应用意
识.
2.经历将实际问题抽象成数学问题解决的过
程,提高学生的观察能力、动手操作能力、
分析解决问题的能力及合作交流的能力.
教学目标
[活动要求]:
请同学们拿出已做好的圆柱
1.在图上标出点A、点B的位置
2.尝试着从点A到点B沿圆柱侧面进行比划,寻找
蚂蚁爬行的所有路径情况。
例 如图所示,有一个圆柱,它的高是12cm,
底面上圆的周长等于18cm,在圆柱下底面的
点A处有一只蚂蚁,它想吃到上底面上与点A
相对的点B处的食物,沿圆柱侧面爬行到B点,
求其爬行的最短路程是多少?
活动一:找出蚂蚁爬行的所有路径的情况
活动二:比较蚂蚁爬行的所有路径哪种情况最短
[活动步骤]:
1.明确圆柱的侧面展开图是什么?
[活动要求]:
沿着点A或点B所在的一条母线将圆柱剪开,观察定位点A、点B的位置,并画出示意图。
3.操作验证
2.猜想点A、点B在侧面展开图中的位置。
活动三:寻求蚂蚁爬行的所有路径中最短路径的求法
反思:求最短路径的方法是什么?
展成平面图形
确定最短路线(即两个点的具体位置)
确定直角三角形
利用勾股定理求解
B
C
A
求最短路径的方法
反思:解决这一类几何型问题的步骤是什么?
解决实际问题的关键是根据实际问题建立相应的数学模型,解决这一类几何型问题的具体步骤大致可以归纳如下:
1.审题——分析实际问题;
2.建模——建立相应的数学模型;
3.求解——运用勾股定理计算;
4.检验——是否符合实际问题的真实性.
反思:解决本题目的关键是什么?
方法提炼
[变式1].
如图,有一圆柱,其高为8cm,它的底面周长为16cm,在圆柱外侧距下底1cm的A处有一只蚂蚁,它想得到距上底1cm 的B处的食物,则蚂蚁经过的最短路程是多少?
小试牛刀
[变式2].
有一圆柱形油罐如图所示,已知油罐的底面圆半径是2米,高为5米,要从A点起环绕油罐建梯子,梯子的顶端正好到达A点的正上方B点,则梯子最少需要多少米(∏=3).
小试牛刀
[变式3].
我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是 多少 尺?
小试牛刀
如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为多少 m(容器厚度忽略不计).
思维加油站
1.本节课你学习了哪些知识?有哪些收获?体
现了什么数学思想?
2. 请填写学习评价表:你本节课的表现( )
A.优秀 B.良好 C.合格
盘点收获
谢谢大家
再见
