沪科版数学七年级上册 1.6 有理数的乘方课件(共42张PPT)
文档属性
| 名称 | 沪科版数学七年级上册 1.6 有理数的乘方课件(共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 944.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 00:00:00 | ||
图片预览








文档简介
(共42张PPT)
1.6 有理数的乘方
“你真傻就要这些米粒”国王哈哈大笑 ,他下令将一袋米拿到宝座前.计数米粒的工作开始了.第一格内放一粒,第二格两粒,第三格四粒……还没到第二十格,袋子已经空了.一袋又一袋的米被扛到国王面前来,但是,米粒数一格接一格地增长得那么迅速,很快国王就看出,即使拿来全印度的米,他也无法兑现他对宰相许下的诺言!这位聪明的宰相到底要求的是多少米粒呢?
第1格:1
第2格:2
第3格:4=2x2
第4格:8=2x2x2
第5格:16=2x2x2x2
……
63个2
第64格=2x2x2x……x2
想一想
有没有简单的记法和读法???
这些麦子究竟有多少?打个比方,如果造一个仓库来放这些麦子,仓库高4公尺,宽10公尺,那么仓库的长度就等于地球到太阳的距离的两倍。而要生产这么多的麦子,全世界要两千年。
尽管印度舍罕王非常富有,但要这样多的麦子他是怎么也拿不出来的。这么一来,舍罕王就欠了宰相好大一笔债。要么是忍受达依尔没完没了的讨债,要么是干脆砍掉他的脑袋。结果究竟如何,可惜史书上没有记载。
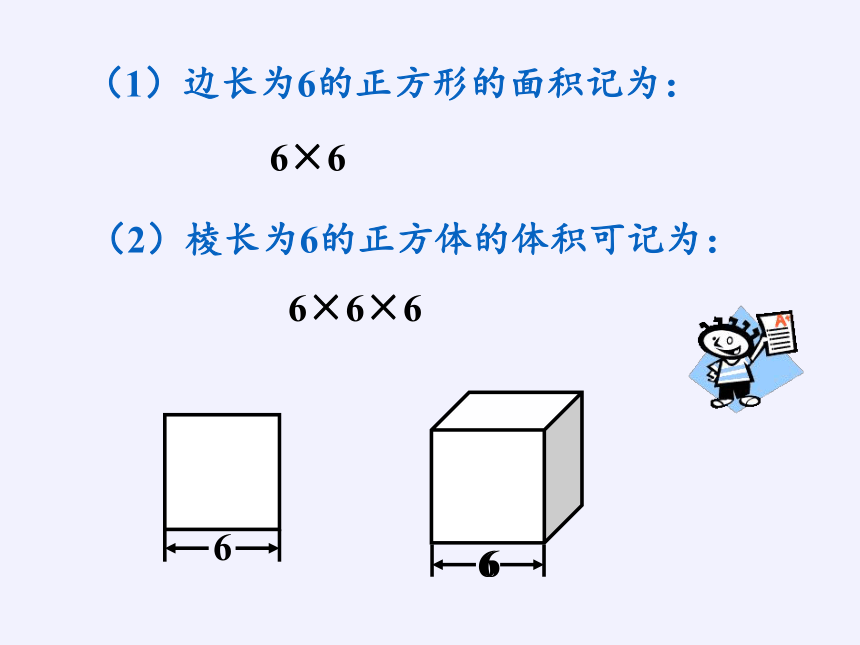
(1)边长为6的正方形的面积记为:
(2)棱长为6的正方体的体积可记为:
6×6
6×6×6
6
6
6
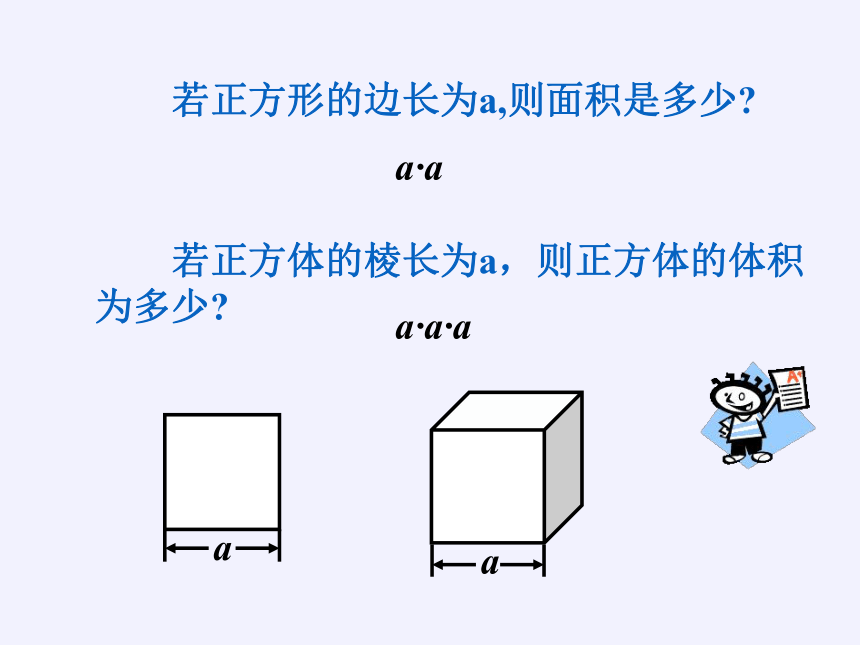
若正方形的边长为a,则面积是多少
若正方体的棱长为a,则正方体的体积为多少
a·a
a·a·a
a
a
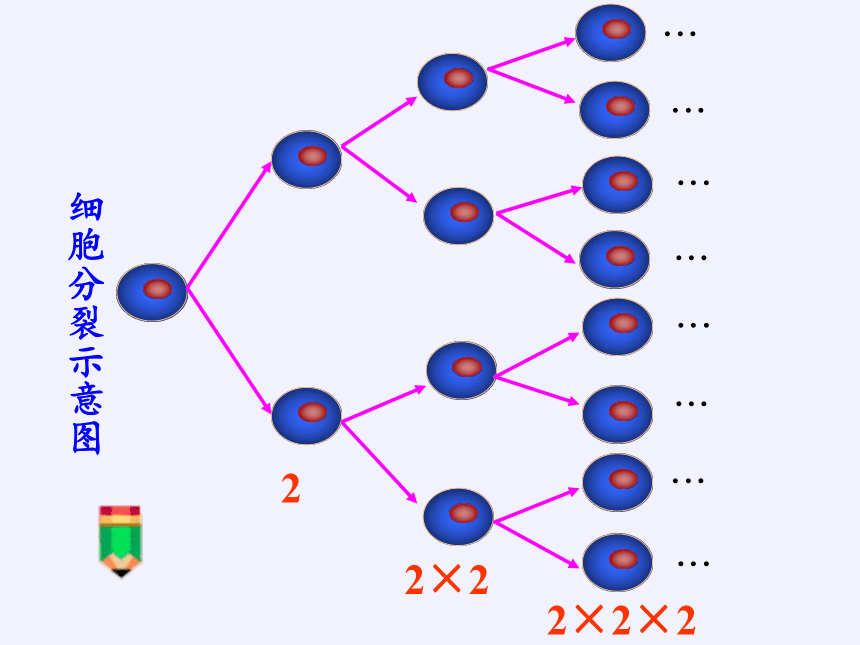
细胞分裂示意图
2
2×2
2×2×2
···
···
···
···
···
···
···
···
1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?
2×2×·······×2×2
10个2
2×2×… ×2×2
10个
记作62,读作6的平方(或二次方).
6×6
6×6×6
a·a
a·a·a
记作210,读作2的10次方.
记作a3,读作a的立方(或三次方).
记作a2,读作a的平方(或二次方).
记作63,读作6的立方(或三次方).
一般地,n个相同因数a相乘,即:
记作:an,读作a的n次方.
或者a的n次幂
a×a ×… ×a ×a
n个
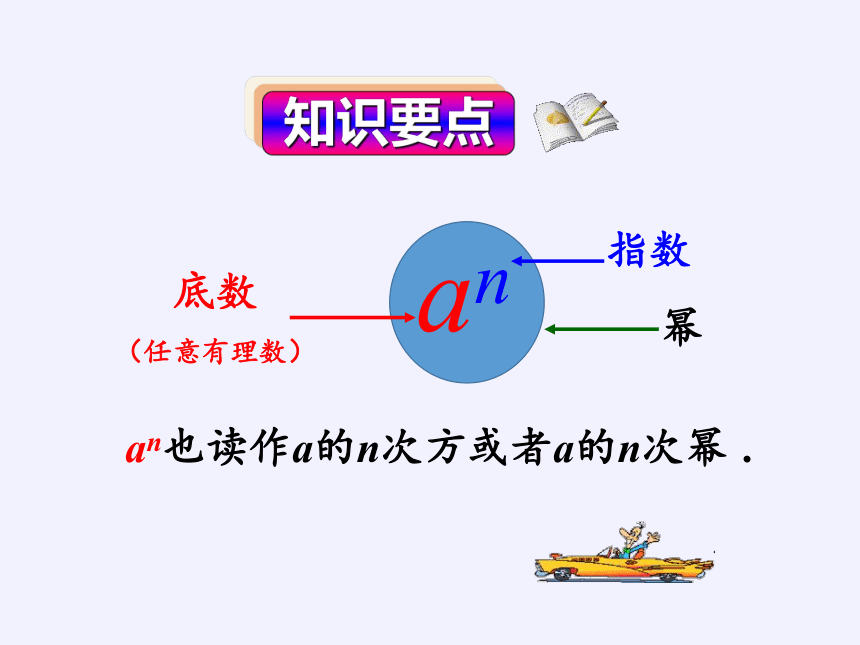
知识要点
知识要点
求n个相同因数a的积的运算叫做乘方.
即:
an=
a×a ×… ×a ×a
n个
知识要点
an
底数
(任意有理数)
指数
幂
an也读作a的n次方或者a的n次幂 .
记作
n个
记作
记作
记作
a的平方
a的2次幂
a的二次方
a的立方
a的3次幂
a的三次方
a的4次幂
a的四次方
a的n次幂
a的n次方
读作
读作
读作
读作
(1) 34 读做__________,其中底数是___,指数是___,表示为___________,结果为_____.
(2) 读做____________,其中底数是_____,指数是_____,表示为_________________,结果为______.
3的4次幂
3
3×3×3×3
81
4
3
练一练
一个数可以看作这个数本身的一次方.
a的底数,指数各是多少?
a的底数是a,指数是1.
想一想
(1)71有意义吗?
(2)12000与15有什么异同?
(3)02000有意义吗?
想一想
0的任何次幂等于零;
1的任何次幂等于1.
归纳
(1)(-5)3 ; (2)(-1)4;
(3) ; (4)(-3)5;
(5)43 ; (6)34 .
观察各题的结果,你能发现什么规律?
正数的任何次幂是正数;
负数的奇次幂是负数,负数的偶次幂是正数.
计算 :
-125
1
64
243
81
(-4)2与-42
观察下面两个式子有什么不同?
(-4)2表示-4的平方,-42表示4的平方的相反数.
当底数是负数或分数时,底数一定要加上括号.
(1)(-1)5=_________,
(2)(-1)8=_________,
(3)12000= ____________,
(4)02005=_____________,
(5)(-10)4=_________,
(6)(-5)3=__________.
口算下列各题:
-1
1
1
0
10 000
-125
归纳
运算名称 运算结果
加法 和
减法 差
乘法 积
除法 商
乘方 幂
例1:计算:
解:
45>54.
想一想
一个大于1的正数作底数,指数越大,乘方的结果越大;
而一个小于1的正数作底数,指数越大,乘方的结果就越小 .
归纳
例2:用计算器计算
解:用带符号键 的计算器.
(-)
(-)
(
9
∧
=
531 441.
(-)
(
7
∧
=
-16807.
显示:(-9)∧6
显示:(-7)∧5
用计算器计算:
262 144
279 936
20 736
9 924.36543
练一练
3+52×(-7)这个式子中,存在哪几种计算?这道题按什么顺序计算?
存在+、×和乘方的运算.根据前面学过的有理数的加减乘除混合运算法则,我们应该“先乘除,后加减”来计算这个式子.那么乘方的运算顺序我们又是怎么规定的呢?
有理数的混合运算应注意的运算顺序:
(1)先乘方,再乘除,最后加减;
(2)同级运算,从左到右进行;
(3)如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
知识要点
例3:计算:
例3 计算:
例4:观察下面三行数:
-3,9,-27,81,-243,729,…;①
0,12,-24,84,-240,733,…;②
10,-17,55,-181,487,-1557,…;③
(1)第①行数按什么规律排列?
(2)第② ③行数与第①行数分别有什么关系?
(3)取每行数的第9个数,计算这三个数的和.
解:(1)第①行数是-3,(-3)2 ,(-3)3,(-3)4,···.
(2)对比①②两行中位置对应的数,将会发现第②行数是第①行相应的数加3,即
-3+3,(-3)2+3 ,(-3)3+3,(-3)4+3,···.
对比①③两行中位置对应的数,将会发现第③行数是第①行对应的数的2倍再加1,即
-3×2+1,(-3)2×2+1 ,(-3)3×2+1,(-3)4×2+1,···.
(3)每行数中的第9个数的和是:
(-3)9+[(-3)9+3] + [(-3)9×2+1]
=-19 683+(-19683+3) +(-19683) ×2+1
=-19 683-19 680-39 366+1
=-78 728.
指数
底数
幂
负数的奇次幂是负数,负数的偶次幂是正数. 正数的任何次幂都是正数,0的任何次幂都是0.
课堂小结
有理数的混合运算应注意的运算顺序:
(1)先乘方,再乘除,最后加减;
(2)同级运算,从左到右进行;
(3)如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
1.把下列各式写成乘方运算的形式,并指出底数,指数各是多少?
(2)底数分别为:
(3)指数分别为:5,4,1000.
随堂练习
2.如果一个数的偶次幂是正数,那么这个数是( )
A.正数 B.负数
C.有理数 D.非0数
3.如果有理数a满足a2A.绝对值小于1的数 B.大于1的数
C.小于-1的数 D.0和1之间的数
D
D
4.计算:
5.已知m=b1+b2+b3+b4+···+b1000,
当b=-1时,求m5的值.
解:当b=-1时,
m=b1+b2+b3+b4+···+b1000
=(-1) 1+ (-1) 2+ (-1) 3 + (-1)4 + ···+ (-1)1000
=-1+1-1+1 - ···-1+1
=0.
所以m5=05=0.
谢 谢
1.6 有理数的乘方
“你真傻就要这些米粒”国王哈哈大笑 ,他下令将一袋米拿到宝座前.计数米粒的工作开始了.第一格内放一粒,第二格两粒,第三格四粒……还没到第二十格,袋子已经空了.一袋又一袋的米被扛到国王面前来,但是,米粒数一格接一格地增长得那么迅速,很快国王就看出,即使拿来全印度的米,他也无法兑现他对宰相许下的诺言!这位聪明的宰相到底要求的是多少米粒呢?
第1格:1
第2格:2
第3格:4=2x2
第4格:8=2x2x2
第5格:16=2x2x2x2
……
63个2
第64格=2x2x2x……x2
想一想
有没有简单的记法和读法???
这些麦子究竟有多少?打个比方,如果造一个仓库来放这些麦子,仓库高4公尺,宽10公尺,那么仓库的长度就等于地球到太阳的距离的两倍。而要生产这么多的麦子,全世界要两千年。
尽管印度舍罕王非常富有,但要这样多的麦子他是怎么也拿不出来的。这么一来,舍罕王就欠了宰相好大一笔债。要么是忍受达依尔没完没了的讨债,要么是干脆砍掉他的脑袋。结果究竟如何,可惜史书上没有记载。
(1)边长为6的正方形的面积记为:
(2)棱长为6的正方体的体积可记为:
6×6
6×6×6
6
6
6
若正方形的边长为a,则面积是多少
若正方体的棱长为a,则正方体的体积为多少
a·a
a·a·a
a
a
细胞分裂示意图
2
2×2
2×2×2
···
···
···
···
···
···
···
···
1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?
2×2×·······×2×2
10个2
2×2×… ×2×2
10个
记作62,读作6的平方(或二次方).
6×6
6×6×6
a·a
a·a·a
记作210,读作2的10次方.
记作a3,读作a的立方(或三次方).
记作a2,读作a的平方(或二次方).
记作63,读作6的立方(或三次方).
一般地,n个相同因数a相乘,即:
记作:an,读作a的n次方.
或者a的n次幂
a×a ×… ×a ×a
n个
知识要点
知识要点
求n个相同因数a的积的运算叫做乘方.
即:
an=
a×a ×… ×a ×a
n个
知识要点
an
底数
(任意有理数)
指数
幂
an也读作a的n次方或者a的n次幂 .
记作
n个
记作
记作
记作
a的平方
a的2次幂
a的二次方
a的立方
a的3次幂
a的三次方
a的4次幂
a的四次方
a的n次幂
a的n次方
读作
读作
读作
读作
(1) 34 读做__________,其中底数是___,指数是___,表示为___________,结果为_____.
(2) 读做____________,其中底数是_____,指数是_____,表示为_________________,结果为______.
3的4次幂
3
3×3×3×3
81
4
3
练一练
一个数可以看作这个数本身的一次方.
a的底数,指数各是多少?
a的底数是a,指数是1.
想一想
(1)71有意义吗?
(2)12000与15有什么异同?
(3)02000有意义吗?
想一想
0的任何次幂等于零;
1的任何次幂等于1.
归纳
(1)(-5)3 ; (2)(-1)4;
(3) ; (4)(-3)5;
(5)43 ; (6)34 .
观察各题的结果,你能发现什么规律?
正数的任何次幂是正数;
负数的奇次幂是负数,负数的偶次幂是正数.
计算 :
-125
1
64
243
81
(-4)2与-42
观察下面两个式子有什么不同?
(-4)2表示-4的平方,-42表示4的平方的相反数.
当底数是负数或分数时,底数一定要加上括号.
(1)(-1)5=_________,
(2)(-1)8=_________,
(3)12000= ____________,
(4)02005=_____________,
(5)(-10)4=_________,
(6)(-5)3=__________.
口算下列各题:
-1
1
1
0
10 000
-125
归纳
运算名称 运算结果
加法 和
减法 差
乘法 积
除法 商
乘方 幂
例1:计算:
解:
45>54.
想一想
一个大于1的正数作底数,指数越大,乘方的结果越大;
而一个小于1的正数作底数,指数越大,乘方的结果就越小 .
归纳
例2:用计算器计算
解:用带符号键 的计算器.
(-)
(-)
(
9
∧
=
531 441.
(-)
(
7
∧
=
-16807.
显示:(-9)∧6
显示:(-7)∧5
用计算器计算:
262 144
279 936
20 736
9 924.36543
练一练
3+52×(-7)这个式子中,存在哪几种计算?这道题按什么顺序计算?
存在+、×和乘方的运算.根据前面学过的有理数的加减乘除混合运算法则,我们应该“先乘除,后加减”来计算这个式子.那么乘方的运算顺序我们又是怎么规定的呢?
有理数的混合运算应注意的运算顺序:
(1)先乘方,再乘除,最后加减;
(2)同级运算,从左到右进行;
(3)如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
知识要点
例3:计算:
例3 计算:
例4:观察下面三行数:
-3,9,-27,81,-243,729,…;①
0,12,-24,84,-240,733,…;②
10,-17,55,-181,487,-1557,…;③
(1)第①行数按什么规律排列?
(2)第② ③行数与第①行数分别有什么关系?
(3)取每行数的第9个数,计算这三个数的和.
解:(1)第①行数是-3,(-3)2 ,(-3)3,(-3)4,···.
(2)对比①②两行中位置对应的数,将会发现第②行数是第①行相应的数加3,即
-3+3,(-3)2+3 ,(-3)3+3,(-3)4+3,···.
对比①③两行中位置对应的数,将会发现第③行数是第①行对应的数的2倍再加1,即
-3×2+1,(-3)2×2+1 ,(-3)3×2+1,(-3)4×2+1,···.
(3)每行数中的第9个数的和是:
(-3)9+[(-3)9+3] + [(-3)9×2+1]
=-19 683+(-19683+3) +(-19683) ×2+1
=-19 683-19 680-39 366+1
=-78 728.
指数
底数
幂
负数的奇次幂是负数,负数的偶次幂是正数. 正数的任何次幂都是正数,0的任何次幂都是0.
课堂小结
有理数的混合运算应注意的运算顺序:
(1)先乘方,再乘除,最后加减;
(2)同级运算,从左到右进行;
(3)如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
1.把下列各式写成乘方运算的形式,并指出底数,指数各是多少?
(2)底数分别为:
(3)指数分别为:5,4,1000.
随堂练习
2.如果一个数的偶次幂是正数,那么这个数是( )
A.正数 B.负数
C.有理数 D.非0数
3.如果有理数a满足a2
C.小于-1的数 D.0和1之间的数
D
D
4.计算:
5.已知m=b1+b2+b3+b4+···+b1000,
当b=-1时,求m5的值.
解:当b=-1时,
m=b1+b2+b3+b4+···+b1000
=(-1) 1+ (-1) 2+ (-1) 3 + (-1)4 + ···+ (-1)1000
=-1+1-1+1 - ···-1+1
=0.
所以m5=05=0.
谢 谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
