人教版数学七年级上册_4.2直线、射线、线段(第2课时)教学PPT17张
文档属性
| 名称 | 人教版数学七年级上册_4.2直线、射线、线段(第2课时)教学PPT17张 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 09:05:58 | ||
图片预览



文档简介
(共17张PPT)
直线、射线、线段(二)
(1)线段AB长2厘米,线段CD长3厘米,则AB _____ CD (填<或>或=).
(2)线段AB和CD分别长2.5 cm和2.3 cm ,则AB______CD(填<或>或=).
<
>
认真阅读课本第126页至第128页的内容,完成下面练习并体验知识点的形成过程.
1、 比较两条线段长短的方法
(1)度量法:用_________分别测量出它们的长度来比较.
(2)叠合法:把其中的一条线段_______另一条上作比较.
思考:画在黑板上的两条线段是无法移动的,在没有度量工具的情况下,请大家想想办法,如何来比较它们的长短?
这就是我们接下来学习得内容:利用圆规比较线段的长短
移到
刻度尺
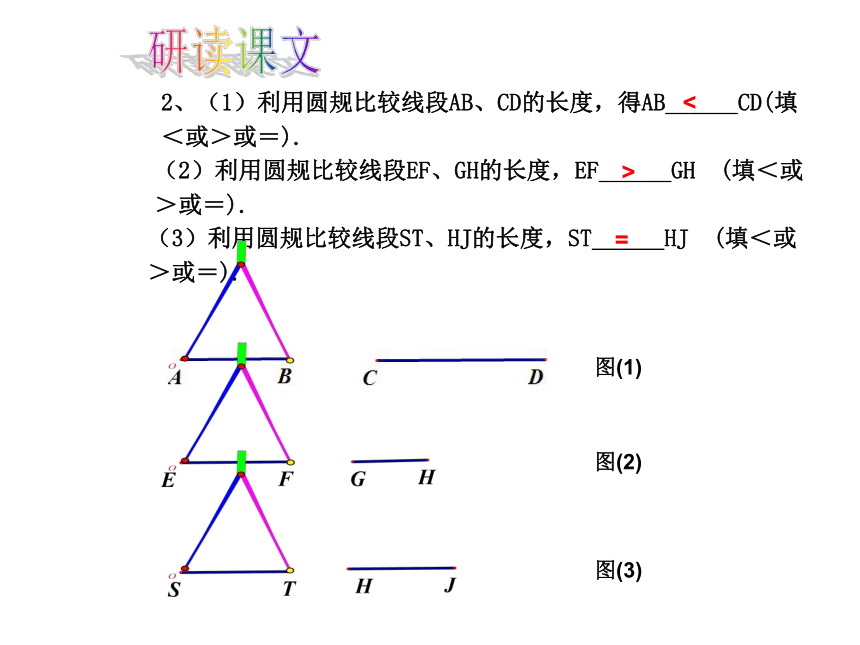
2、(1)利用圆规比较线段AB、CD的长度,得AB______CD(填<或>或=).
(2)利用圆规比较线段EF、GH的长度,EF______GH (填<或>或=).
(3)利用圆规比较线段ST、HJ的长度,ST______HJ (填<或>或=).
图(1)
图(2)
图(3)
<
>
=
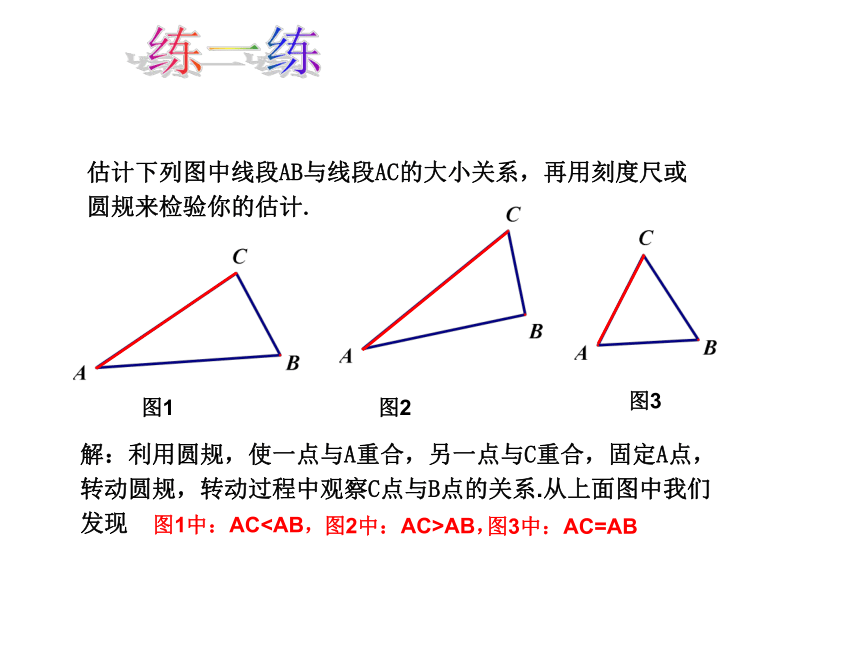
估计下列图中线段AB与线段AC的大小关系,再用刻度尺或圆规来检验你的估计.
图1
图2
图3
解:利用圆规,使一点与A重合,另一点与C重合,固定A点,转动圆规,转动过程中观察C点与B点的关系.从上面图中我们发现
图1中:AC图2中:AC>AB,
图3中:AC=AB
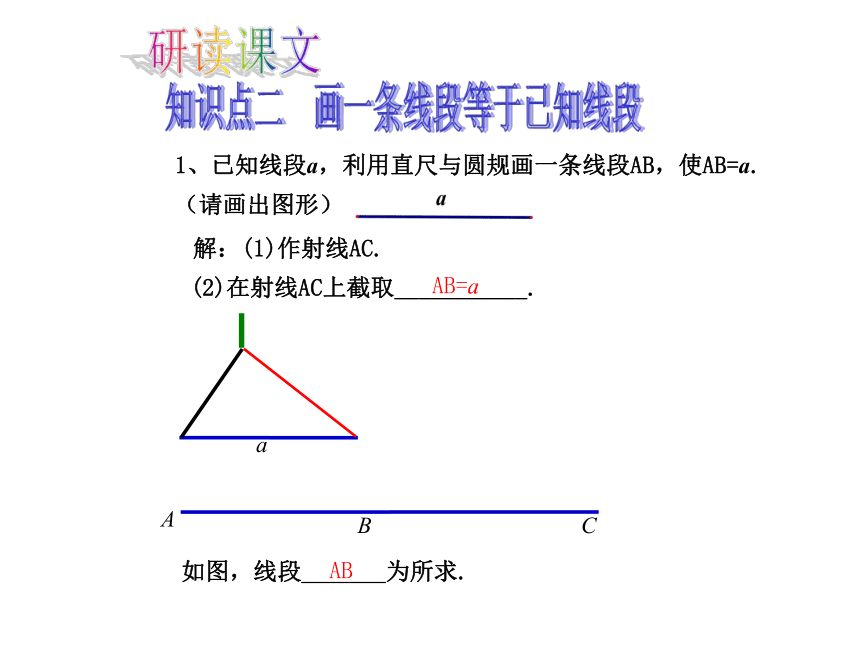
1、已知线段a,利用直尺与圆规画一条线段AB,使AB=a.(请画出图形)
解:(1)作射线AC.
a
C
A
B
(2)在射线AC上截取___________.
AB=a
如图,线段_______为所求.
AB
a
C
A
M
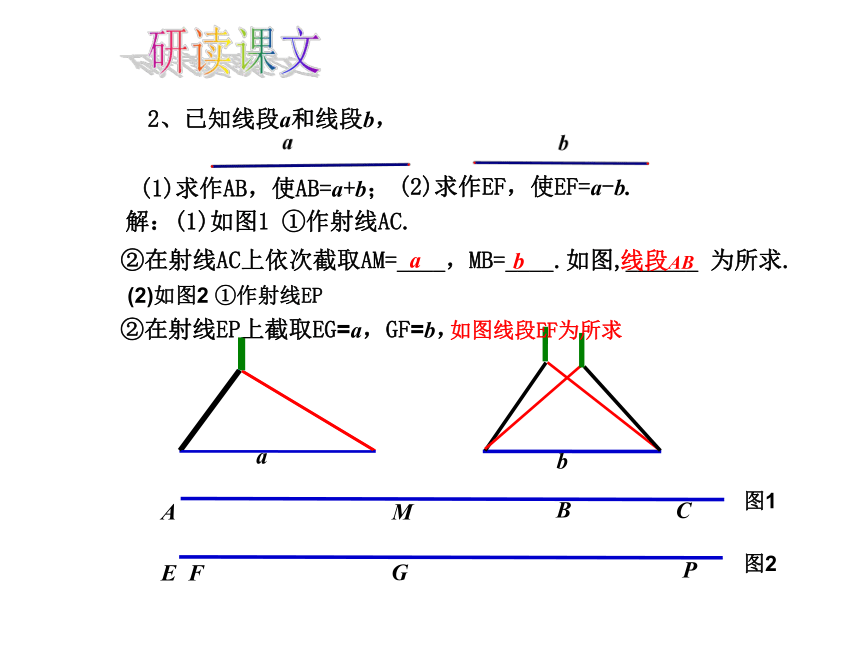
2、已知线段a和线段b,
(1)求作AB,使AB=a+b;
解:(1)如图1 ①作射线AC.
②在射线AC上依次截取AM=____,MB=____.如图,______ 为所求.
b
B
a
b
线段AB
(2)求作EF,使EF=a-b.
(2)如图2 ①作射线EP
②在射线EP上截取EG=a,GF=b,
E
P
G
F
图1
图2
如图线段EF为所求
如图,已知线段a、b画一条线段,使它等于2a-b.
解:(1)作射线OP;
(2)在射线OP上依次截取OA=a,AB=a;
(3)截取BC=b,
a
O
b
A
P
C
B
则OC=2a-b,OC就是所求的线段.
1、把一条线段分成________的两条线段的点叫做这条线段的中点.如C是AB的中点,则AC=______=_____AB.
2、类似地,还有线段的三等分点、四等分点等.
如图,已知C为线段AB的中点,D为线段AC的中点,若AB=4cm,求线段CD的长度.
解:因为AB=4cm,C是AB的中点,
所以AC= AB =2cm;
因为D是AC的中点,
所以CD= AC=1cm
相等
BC
认真阅读课本第128页的“思考”至第129页的内容,完成下面练习,并体验知识点的形成过程.
思考:如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你联系以前所学的知识,在图上画出最短路线.
A
B
两点之间,线段最短
1、两点的所有连线中,_____________. 简单说成,______________________.
2、_____________________________,叫做这两点的距离.
直线距离最短
两点之间,线段最短
两点之间的线段的长度
1、如图点C、点B在线段AD上,且AB=CD,那么AC与BD的大小关系是( )
A、AC=BD B、AC<BD
C、AC>BD D、不能确定
2、如图,AC=CD=DE=EB,图中和线段AD长度相等的线段是______________.以D为中点的线段_________.
A
CE、DB
CE、AB
3、如果点M在线段AC上,下列表达式中能表示点M是线段AC中点的有( )
①AM=MC; ②AM= AC;
③AC=2AM; ④AM+MC=AC
A.1个 B.2个 C.3个 D.4个
4、观察下图,填空:
(1)AD=____+BC+____=AC+____=AB+____
(2)CD=_______-AC
(3)BC=AC-______
(4)AC______CD (填<或>)
C
BD
>
AB
AD
CD
CD
AB
两点之间,线段最短
1、把甲、乙两地间一段弯曲的公路改为直路,可以缩短路程,其理由是____________.
两点之间,线段最短
两点之间,线段最短
2、如图:AB+AC_____BC,
理由是:
__________________________.
>
三角形两边之和大于第三边
学习从来无捷径,
循序渐进登高峰。
———— 高永祚
直线、射线、线段(二)
(1)线段AB长2厘米,线段CD长3厘米,则AB _____ CD (填<或>或=).
(2)线段AB和CD分别长2.5 cm和2.3 cm ,则AB______CD(填<或>或=).
<
>
认真阅读课本第126页至第128页的内容,完成下面练习并体验知识点的形成过程.
1、 比较两条线段长短的方法
(1)度量法:用_________分别测量出它们的长度来比较.
(2)叠合法:把其中的一条线段_______另一条上作比较.
思考:画在黑板上的两条线段是无法移动的,在没有度量工具的情况下,请大家想想办法,如何来比较它们的长短?
这就是我们接下来学习得内容:利用圆规比较线段的长短
移到
刻度尺
2、(1)利用圆规比较线段AB、CD的长度,得AB______CD(填<或>或=).
(2)利用圆规比较线段EF、GH的长度,EF______GH (填<或>或=).
(3)利用圆规比较线段ST、HJ的长度,ST______HJ (填<或>或=).
图(1)
图(2)
图(3)
<
>
=
估计下列图中线段AB与线段AC的大小关系,再用刻度尺或圆规来检验你的估计.
图1
图2
图3
解:利用圆规,使一点与A重合,另一点与C重合,固定A点,转动圆规,转动过程中观察C点与B点的关系.从上面图中我们发现
图1中:AC
图3中:AC=AB
1、已知线段a,利用直尺与圆规画一条线段AB,使AB=a.(请画出图形)
解:(1)作射线AC.
a
C
A
B
(2)在射线AC上截取___________.
AB=a
如图,线段_______为所求.
AB
a
C
A
M
2、已知线段a和线段b,
(1)求作AB,使AB=a+b;
解:(1)如图1 ①作射线AC.
②在射线AC上依次截取AM=____,MB=____.如图,______ 为所求.
b
B
a
b
线段AB
(2)求作EF,使EF=a-b.
(2)如图2 ①作射线EP
②在射线EP上截取EG=a,GF=b,
E
P
G
F
图1
图2
如图线段EF为所求
如图,已知线段a、b画一条线段,使它等于2a-b.
解:(1)作射线OP;
(2)在射线OP上依次截取OA=a,AB=a;
(3)截取BC=b,
a
O
b
A
P
C
B
则OC=2a-b,OC就是所求的线段.
1、把一条线段分成________的两条线段的点叫做这条线段的中点.如C是AB的中点,则AC=______=_____AB.
2、类似地,还有线段的三等分点、四等分点等.
如图,已知C为线段AB的中点,D为线段AC的中点,若AB=4cm,求线段CD的长度.
解:因为AB=4cm,C是AB的中点,
所以AC= AB =2cm;
因为D是AC的中点,
所以CD= AC=1cm
相等
BC
认真阅读课本第128页的“思考”至第129页的内容,完成下面练习,并体验知识点的形成过程.
思考:如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你联系以前所学的知识,在图上画出最短路线.
A
B
两点之间,线段最短
1、两点的所有连线中,_____________. 简单说成,______________________.
2、_____________________________,叫做这两点的距离.
直线距离最短
两点之间,线段最短
两点之间的线段的长度
1、如图点C、点B在线段AD上,且AB=CD,那么AC与BD的大小关系是( )
A、AC=BD B、AC<BD
C、AC>BD D、不能确定
2、如图,AC=CD=DE=EB,图中和线段AD长度相等的线段是______________.以D为中点的线段_________.
A
CE、DB
CE、AB
3、如果点M在线段AC上,下列表达式中能表示点M是线段AC中点的有( )
①AM=MC; ②AM= AC;
③AC=2AM; ④AM+MC=AC
A.1个 B.2个 C.3个 D.4个
4、观察下图,填空:
(1)AD=____+BC+____=AC+____=AB+____
(2)CD=_______-AC
(3)BC=AC-______
(4)AC______CD (填<或>)
C
BD
>
AB
AD
CD
CD
AB
两点之间,线段最短
1、把甲、乙两地间一段弯曲的公路改为直路,可以缩短路程,其理由是____________.
两点之间,线段最短
两点之间,线段最短
2、如图:AB+AC_____BC,
理由是:
__________________________.
>
三角形两边之和大于第三边
学习从来无捷径,
循序渐进登高峰。
———— 高永祚
