八年级数学等腰三角形
图片预览








文档简介
(共30张PPT)
12.3.2.1等边三角形(1)
我们在上一节学习了等腰三角形的性质。现在能回答一些问题吗?
一、复习:
1、等腰三角形的性质定理是什么?
等腰三角形的两个底角相等。
(可以简称:等边对等角)
2、这个定理的逆命题是什么?
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
等腰三角形的判定定理
如果一个三角形有两个角相等,那么这个三角形是等腰三角形。
简写成:等角对等边
等腰三角形的判定定理 与性质定理有何不同?
探究:
等腰三角形的性质定理和判定定理 互为逆命题
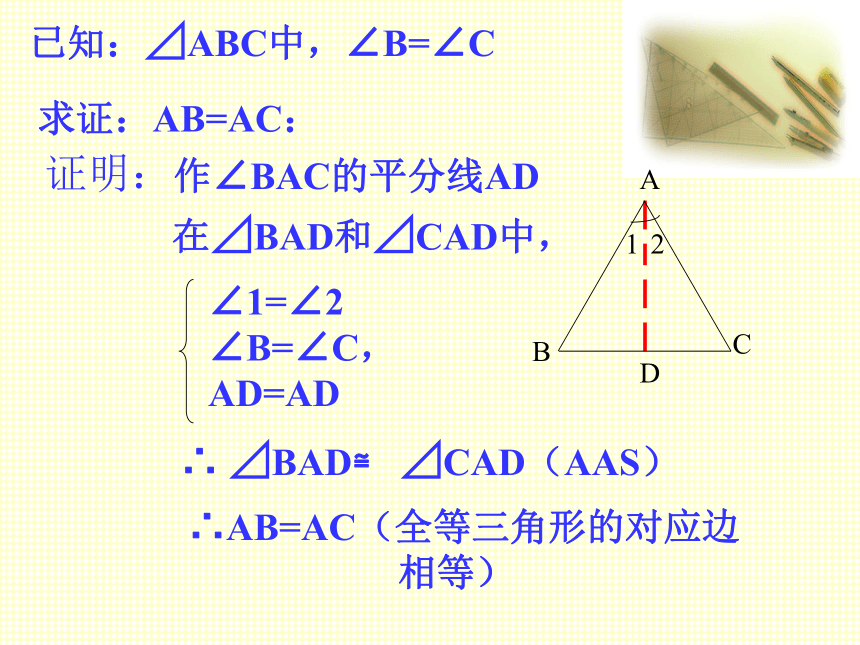
已知:⊿ABC中,∠B=∠C
求证:AB=AC:
证明:
作∠BAC的平分线AD
在⊿BAD和⊿CAD中,
∠1=∠2
∠B=∠C,
AD=AD
∴ ⊿BAD≌ ⊿CAD(AAS)
∴AB=AC(全等三角形的对应边
相等)
1
A
B
C
D
2
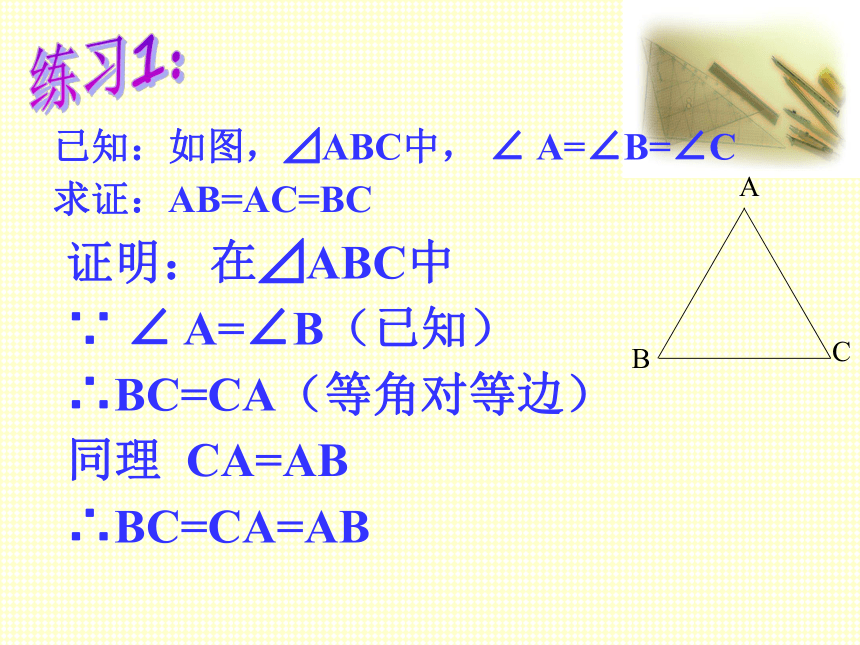
已知:如图,⊿ABC中, ∠ A=∠B=∠C
求证:AB=AC=BC
A
B
C
证明:在⊿ABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理 CA=AB
∴BC=CA=AB
推论1:
三个角都相等的三角形是等边三角形。
如果一个等腰三角形中有一个角是60°,那么这个三角形是什么三角形?
第一种情况:当顶角是60度时
第二种情况:当底角是60度时
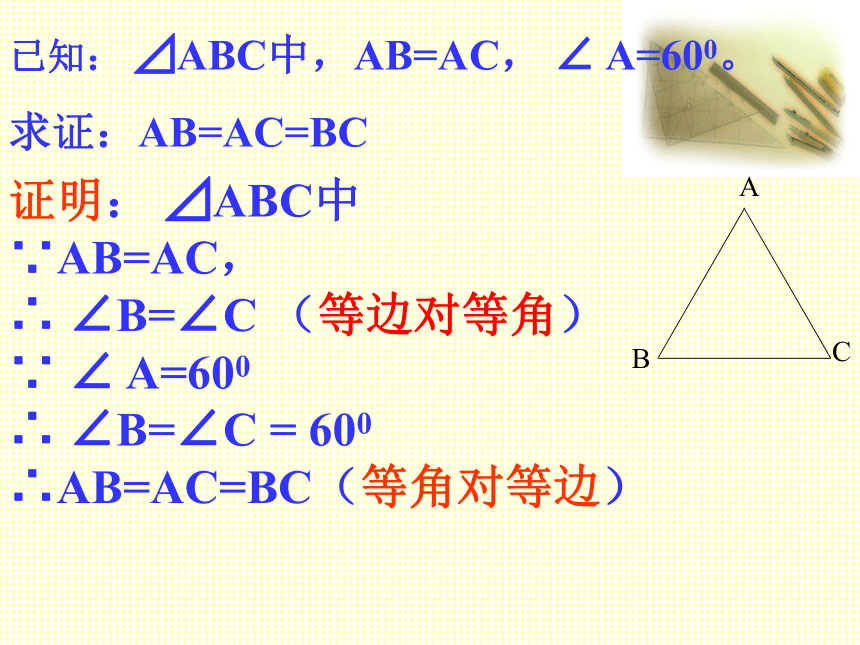
已知: ⊿ABC中,AB=AC, ∠ A=600。
求证:AB=AC=BC
A
B
C
证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ A=600
∴ ∠B=∠C = 600
∴AB=AC=BC(等角对等边)
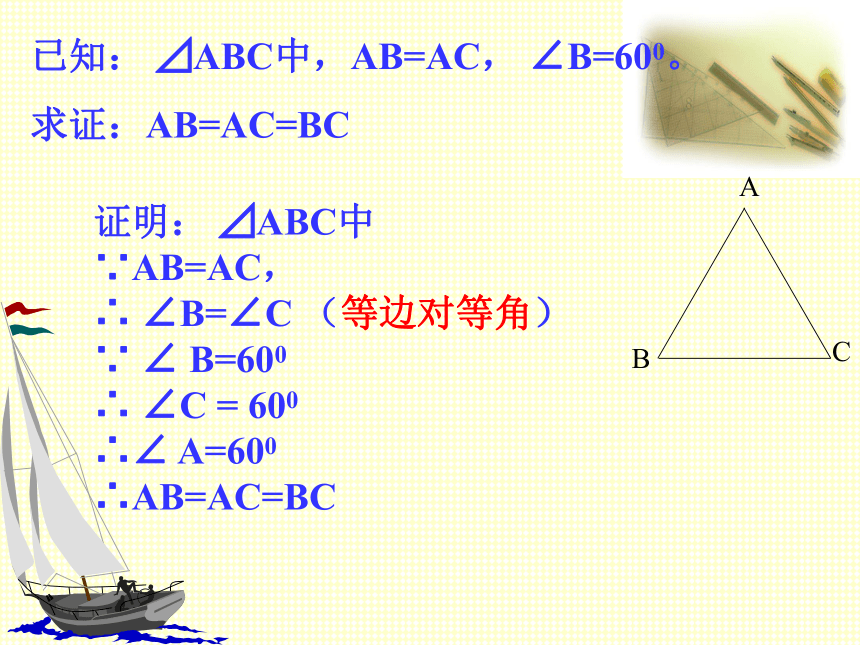
已知: ⊿ABC中,AB=AC, ∠B=600。
求证:AB=AC=BC
A
B
C
证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ B=600
∴ ∠C = 600
∴∠ A=600
∴AB=AC=BC
推论2:
有一个角是 60°的等腰三角形是等边三角形。
例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。
A
B
C
D
E
1
2
如图,∠CAE是⊿ABC的外角,
∠1=∠2,AD∥BC。
已知:
求证:AB=AC
证明:
∵AD∥BC,
∴∠1=∠B(两直线平行,
同位角相等)
∠2=∠C(两直线平行,
内错角相等)
∵∠1=∠2
∴∠B=∠C
∴AB=AC(等边对等角)
A
B
C
D
E
1
2
练习3
C
B
A
D
1
2
解答
已知:如图, ∠A= ∠DBC =360, ∠C=720。计算∠1和∠2,并说明图中有哪些等腰三角形?
解:
∠1=720 ∠2=360
等腰三角形有: ⊿ABC
⊿ABD
⊿BCD
C
B
A
D
1
2
练习4
已知:如图,CD是等腰直角三角形ABC斜边上的高,找出图中有哪些等腰直角三角形。
解答
A
C
D
B
A
C
D
B
解答
等腰直角三角形有: ⊿ABC ⊿ACD ⊿BCD
练习5
B
A
D
C
已知:如图,
AD ∥BC,BD平分∠ABC。
求证:AB=AD
解答
B
A
D
C
证明:∵ AD ∥BC
∴∠ADB=∠DBC
∵∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD(等角对等边)
研究性学习
如果过等腰三角形的一个顶点的直线把原三角形分成两个等腰三角形,那么原等腰三角形的顶角可能是多少度?请你画出图形,并结合图形说明理由。
1、等腰三角形的判定定理及其推论的内容是什么?
判定定理:如果一个三角形有两个角相等,那么这个三角形是等腰三角形。 推论1:三个角都相等的三角形是等边三角形。 推论2:有一个角是 60°的等腰三角形是等边三角形。
2、等腰三角形的判定方法有下列几种:
①定义
②判定定理
3、等边三角形的判定方法有以下几种:
①定义
②推论1
③推论2
4、等腰三角形的判定定理与性质定理的区别是:
条件和结论刚好相反。
5、运用等腰三角形的判定定理时,应注意
在同一个三角形中。
2、等腰三角形的判定方法有下列几种: 。
3、等边三角形的判定方法有以下几种: 。
4、等腰三角形的判定定理与性质定理的区别是 。
5、运用等腰三角形的判定定理时,应注意 。
①定义,②判定定理
条件和结论刚好相反。
在同一个三角形中
①定义,②推论1, ③推论2。
1、等腰三角形的判定定理及其推论的内容是什么?
课堂作业:
课本P81:
第2,3,4题
12.3.2.1等边三角形(1)
我们在上一节学习了等腰三角形的性质。现在能回答一些问题吗?
一、复习:
1、等腰三角形的性质定理是什么?
等腰三角形的两个底角相等。
(可以简称:等边对等角)
2、这个定理的逆命题是什么?
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
等腰三角形的判定定理
如果一个三角形有两个角相等,那么这个三角形是等腰三角形。
简写成:等角对等边
等腰三角形的判定定理 与性质定理有何不同?
探究:
等腰三角形的性质定理和判定定理 互为逆命题
已知:⊿ABC中,∠B=∠C
求证:AB=AC:
证明:
作∠BAC的平分线AD
在⊿BAD和⊿CAD中,
∠1=∠2
∠B=∠C,
AD=AD
∴ ⊿BAD≌ ⊿CAD(AAS)
∴AB=AC(全等三角形的对应边
相等)
1
A
B
C
D
2
已知:如图,⊿ABC中, ∠ A=∠B=∠C
求证:AB=AC=BC
A
B
C
证明:在⊿ABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理 CA=AB
∴BC=CA=AB
推论1:
三个角都相等的三角形是等边三角形。
如果一个等腰三角形中有一个角是60°,那么这个三角形是什么三角形?
第一种情况:当顶角是60度时
第二种情况:当底角是60度时
已知: ⊿ABC中,AB=AC, ∠ A=600。
求证:AB=AC=BC
A
B
C
证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ A=600
∴ ∠B=∠C = 600
∴AB=AC=BC(等角对等边)
已知: ⊿ABC中,AB=AC, ∠B=600。
求证:AB=AC=BC
A
B
C
证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ B=600
∴ ∠C = 600
∴∠ A=600
∴AB=AC=BC
推论2:
有一个角是 60°的等腰三角形是等边三角形。
例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。
A
B
C
D
E
1
2
如图,∠CAE是⊿ABC的外角,
∠1=∠2,AD∥BC。
已知:
求证:AB=AC
证明:
∵AD∥BC,
∴∠1=∠B(两直线平行,
同位角相等)
∠2=∠C(两直线平行,
内错角相等)
∵∠1=∠2
∴∠B=∠C
∴AB=AC(等边对等角)
A
B
C
D
E
1
2
练习3
C
B
A
D
1
2
解答
已知:如图, ∠A= ∠DBC =360, ∠C=720。计算∠1和∠2,并说明图中有哪些等腰三角形?
解:
∠1=720 ∠2=360
等腰三角形有: ⊿ABC
⊿ABD
⊿BCD
C
B
A
D
1
2
练习4
已知:如图,CD是等腰直角三角形ABC斜边上的高,找出图中有哪些等腰直角三角形。
解答
A
C
D
B
A
C
D
B
解答
等腰直角三角形有: ⊿ABC ⊿ACD ⊿BCD
练习5
B
A
D
C
已知:如图,
AD ∥BC,BD平分∠ABC。
求证:AB=AD
解答
B
A
D
C
证明:∵ AD ∥BC
∴∠ADB=∠DBC
∵∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD(等角对等边)
研究性学习
如果过等腰三角形的一个顶点的直线把原三角形分成两个等腰三角形,那么原等腰三角形的顶角可能是多少度?请你画出图形,并结合图形说明理由。
1、等腰三角形的判定定理及其推论的内容是什么?
判定定理:如果一个三角形有两个角相等,那么这个三角形是等腰三角形。 推论1:三个角都相等的三角形是等边三角形。 推论2:有一个角是 60°的等腰三角形是等边三角形。
2、等腰三角形的判定方法有下列几种:
①定义
②判定定理
3、等边三角形的判定方法有以下几种:
①定义
②推论1
③推论2
4、等腰三角形的判定定理与性质定理的区别是:
条件和结论刚好相反。
5、运用等腰三角形的判定定理时,应注意
在同一个三角形中。
2、等腰三角形的判定方法有下列几种: 。
3、等边三角形的判定方法有以下几种: 。
4、等腰三角形的判定定理与性质定理的区别是 。
5、运用等腰三角形的判定定理时,应注意 。
①定义,②判定定理
条件和结论刚好相反。
在同一个三角形中
①定义,②推论1, ③推论2。
1、等腰三角形的判定定理及其推论的内容是什么?
课堂作业:
课本P81:
第2,3,4题
