八年级数学用坐标表示轴对称
图片预览










文档简介
(共35张PPT)
人教版义务教育课程标准实验教科书
哈尔滨市第二十七中
常慎敏
用坐标表示轴对称
教学设计的理念
教学程序的设计
教材分析与处理
教学方式的构建
用坐标表示轴对称
教学设计的理念
教学程序的设计
教材分析与处理
教学方式的构建
新的课程观认为素质教育的根本在于发挥学生的主体因素.让学生自主获取知识,并能形成规律和经验。所以本节课的设计理念是:以活动为主,不锁住学生;以发现为主,不代替学生; 以鼓励为主,不钳制学生.重技能,重过程,重方法.让每位学生都能在自主中求知,在合作中获取,在探究中发展。
用坐标表示轴对称
教材地位与作用
本节课是在学生学习了轴对称及轴对称变换的概念与特征,掌握了平面直角坐标系的相关知识的基础上进行的.教材将轴对称变换的知识与坐标知识进行整合,体现了轴对称在平面直角坐标系中的应用,从数量关系的角度刻画轴对称的内容,把“形”和“数”紧密的结合在一起,是培养学生把坐标思想和图形变换的思想相联系的不可缺少的一节重要内容.
教 材 的 处 理
为了实现认知的螺旋上升,使不同层次的学生得到不同的发展,我对教材进行了整合与创造性的使用,安排了三个不同梯度的探究活动 ,从探究关于坐标轴对称的点入手 ,再到由点构成的线段,继而到由线段组成的多边形,使学生在动手操作与动脑思考的过程中深刻感受数学思想方法的运用. 在此基础上,我又安排了活动四 ,进一步挖掘探究的深度与广度,使轴对称变换知识在平面直角坐标系中得到细化与延伸.
教材分析与处理
教学设计的理念
教学程序的设计
教学方式的构建
掌握关于坐标轴(或关于直线x=m,y=n)对称的两个点的坐标之间的对应关系,会作出一个图形关于坐标轴对称的图形.
知识与技能
过程与方法
通过探究关于坐标轴对称的两个点坐标之间关系的活动,培养学生:作图--观察--猜想--验证--归纳这一研究数学问题的基本方法。
教学目标
教材分析与处理
通过探究活动,培养学生的 主动探究,合作交流的意识,体验探究的甘苦和成功的喜悦。
情感态度与价值观
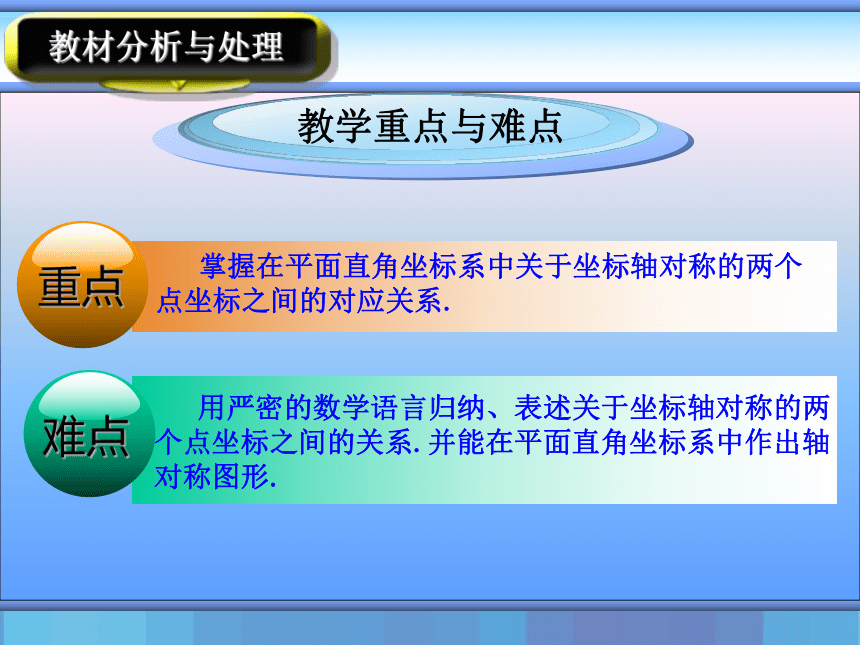
教学重点与难点
掌握在平面直角坐标系中关于坐标轴对称的两个
点坐标之间的对应关系.
重点
用严密的数学语言归纳、表述关于坐标轴对称的两个点坐标之间的关系.并能在平面直角坐标系中作出轴对称图形.
难点
教材分析与处理
用坐标表示轴对称
教 法 分 析
结合学生的认知结构,年龄特征及本节课的特点,采用作图--观察--猜想--验证--归纳为主,多媒体演示为辅的教学方法, 在教学的过程中,设计带有启发性、思考性的问题 ,创设情境,引导学生独立思考,自主探索,合作交流,让学生始终处于一种积极思维、主动探究的学习状态.多媒体教学手段的使用增加了教学的直观性,趣味性,从而加大课堂容量、提高教学效率.
学 法 指 导
在本节课的教学中要帮助学生学会运用观察、分析、比较、归纳、概括等方法去解决问题 .使学习知识和培养能力融为一体.
教 学 手 段
采用多媒体课件及教学材料(方格纸)辅助教学.
教学设计的理念
教学程序的设计
教材分析与处理
教学方式的构建
用坐标表示轴对称
引入新课
创设情境
探索新知
动手实践
思维升华
探究拓展
巩固新知
尝试运用
反思评价
体验收获
课堂延伸
布置作业
教学程序的设计
教学设计的理念
教材分析与处理
教学方式的构建
板书设计
创设情境,引入新课
老北京的地图中,其中西直门和东直门是关于中轴线对称的,如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系, 对应于如图所示的东直门的坐标, 你能找到西直门的位置,说出西直门的坐标吗
右安门
左安门
广安门
广渠门
西便门
东便门
西直门
东直门
阜成门
朝阳门
德胜门
安定门
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
y
永定门
天安门
O
引入新课
创设情境
探索新知
动手实践
提升思维
拓展探究
知识升华
实践应用
课堂延伸
布置作业
板书设计
教学程序的设计
反思评价
体验收获
动手实践,探索新知
在平面直角坐标系上作任意两点.
(1)作出它们关于y轴对称的点,标出点的坐标,填在表格上.
(2) 探究关于y轴对称的点坐标之间的关系,并用数学语言表达出来.
活动一
关于y轴对称 1 2 3 4 5 6 7 8
点
(x1,y1)
对称点(x2,y2)
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A
·
A1 (-2,3)
动手实践,探索新知
y
x
(2,3)
·
动手实践,探索新知
探究结论
关于y 轴对称的点纵坐标相同, 横坐标互为相反数.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
动手实践,探索新知
y
x
(-2,3)
A2
·
(2,3)
A
·
动手实践,探索新知
探究结论
关于y 轴对称的点纵坐标相同,横坐标互为相反数.
关于x轴对称的点横坐标相同,纵坐标互为相反数.
关于哪个轴对称,哪个坐标就不变,另一个坐标互为相反数.
动手实践,探索新知
说出下列各点关于x轴、y轴对称的点的坐标:
(1,3) (-2,6) (-4,-2)
(1,0) (1,-2) (0,-5)
习 题
动手实践,探索新知
在平面直角坐标系上作任意两点A和B,连接AB,再作出A,B两点关于x轴对称的点A1,B1,连接A1,B1 ,你有怎样的发现 关于y轴呢?
活动二
动手实践,探索新知
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
·
·
·
A
B
A1
B1
·
·
C(2,2 )
C1 (2,-2 )
y
x
·
·
A2
B2
·
C2(-2,2 )
动手实践,探索新知
如图,四边形ABCD的四个顶点的坐标分别为A(-5 ,1)、B(-2 , 1)、C(-2 ,5)、D(-5 ,4),分别作出四边形ABCD关于x轴、y轴对称的图形.
活动三
动手实践,探索新知
学习目标
能求出一个点关于坐标轴对称的点的坐标;
能作出一个图形关于坐标轴对称的图形。
引入新课
创设情境
探索新知
动手实践
思维升华
探究拓展
巩固新知
尝试运用
课堂延伸
布置作业
板书设计
教学程序的设计
反思评价
体验收获
拓展探究,提升思维
活动四
如图所示,分别作出△PQR关于直线x=1和直线y=-1对称的图形.
-1
-2
-3
-4
-5
-6
-7
x
y
X=1
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1 0
7
6
5
4
3
2
1
x
y
y=-1
Q
探究拓展,思维升华
探究拓展,思维升华
探究结论
点A(x ,y)
关于直线x=m对称的
点A1的坐标是(x1,y1)
点A(x ,y)
关于直线y=n对称的
点A2的坐标是(x2,y2)
探究拓展,思维升华
探究结论
点A及A1的坐标满足:
(1) x1-m=m-x ;即x1=2m-x
(2) y1 = y
点A(x ,y)关于直线x=m对称
的点A1的坐标是(2m-x,y)
点A及A2的坐标满足:
(1) y2-n = n-y ;即y2=2n-y
(2) x2 = x
点A(x ,y)关于直线y=n对称的
点A2的坐标是(x ,2n-y)
习 题
探究拓展,思维升华
(1)点(-2,-3)关于直线x=-1 的对称点的坐标为 ; 关于直线y=2 的对称点的坐标为 .
(2)点(2,4)与点(4,4)是关于直线 对称的.
引入新课
创设情境
探索新知
动手实践
思维升华
探究拓展
巩固新知
尝试运用
课堂延伸
布置作业
板书设计
教学程序的设计
反思评价
体验收获
尝试运用,巩固新知
(1)若点M(2,a)和点N(a+b,-3)关于x轴对称,试求a,b的值;若这两个点关于y轴对称呢?
(2)已知长方形ABCD关于y轴对称,平行于y轴的边AB长是6,点A的坐标是(-2,-1),请你写出B、C、D三点的坐标.
(3)已知点的坐标A(2,2),B(1,1),C(3,-1.5),D(3,2).请写出A、B两点关于CD对称的点E、F的坐标,并在图中画出这两点.
(4)在坐标系中描出点A(-1,3),B(5,-4),c(-3,-1),D(-1,1),E(-3,5),F(5,8),连接AB,BC,AC,DE,EF,DF,请你判断所得的图形是轴对称图形吗 如果不是,请说明理由,如果是,请说出对称轴.
引入新课
创设情境
探索新知
动手实践
思维升华
探究拓展
巩固新知
尝试运用
课堂延伸
布置作业
板书设计
教学程序的设计
反思评价
体验收获
体验收获,反思评价
知识点
感受
问题
本节课你有哪些收获?
引入新课
创设情境
探索新知
动手实践
思维升华
探究拓展
巩固新知
尝试运用
课堂延伸
布置作业
板书设计
教学程序的设计
反思评价
体验收获
将点(2,1),(5,1),(2,5)做如下变化:
①纵坐标不变,横坐标分别加2.②横坐标不变,纵坐标分别加1.③纵坐标不变,横坐标分别变为原来的2倍.④横坐标不变,纵坐标分别变为原来的2倍.⑤纵坐标不变,横坐标分别乘以-1.⑥横坐标不变,纵坐标分别乘以-1.⑦纵坐标、横都分别乘以-1.
观察变化后的三角形与原三角形有什么变化,并用语言描述出来.
必做题:
布置作业,课堂延伸
选做题:
你能利用本节课的探究的方法,找出一个点关于直线y=x和y=-x对称的点的坐标吗
引入新课
创设情境
探索新知
动手实践
思维升华
探究拓展
巩固新知
尝试运用
课堂延伸
布置作业
板书设计
教学程序的设计
反思评价
体验收获
19.2.2 用坐标表示轴对称
在平面直角坐标系中:
点(x, y)关于x轴对称的点的坐标为(x,-y).
关于y轴对称的点的坐标为(-x, y).
关于直线x=m对称的点的坐标为(2m-x, y)
关于直线y=n对称的点的坐标为(x, 2n- y)
板书设计
人教版义务教育课程标准实验教科书
哈尔滨市第二十七中
常慎敏
用坐标表示轴对称
教学设计的理念
教学程序的设计
教材分析与处理
教学方式的构建
用坐标表示轴对称
教学设计的理念
教学程序的设计
教材分析与处理
教学方式的构建
新的课程观认为素质教育的根本在于发挥学生的主体因素.让学生自主获取知识,并能形成规律和经验。所以本节课的设计理念是:以活动为主,不锁住学生;以发现为主,不代替学生; 以鼓励为主,不钳制学生.重技能,重过程,重方法.让每位学生都能在自主中求知,在合作中获取,在探究中发展。
用坐标表示轴对称
教材地位与作用
本节课是在学生学习了轴对称及轴对称变换的概念与特征,掌握了平面直角坐标系的相关知识的基础上进行的.教材将轴对称变换的知识与坐标知识进行整合,体现了轴对称在平面直角坐标系中的应用,从数量关系的角度刻画轴对称的内容,把“形”和“数”紧密的结合在一起,是培养学生把坐标思想和图形变换的思想相联系的不可缺少的一节重要内容.
教 材 的 处 理
为了实现认知的螺旋上升,使不同层次的学生得到不同的发展,我对教材进行了整合与创造性的使用,安排了三个不同梯度的探究活动 ,从探究关于坐标轴对称的点入手 ,再到由点构成的线段,继而到由线段组成的多边形,使学生在动手操作与动脑思考的过程中深刻感受数学思想方法的运用. 在此基础上,我又安排了活动四 ,进一步挖掘探究的深度与广度,使轴对称变换知识在平面直角坐标系中得到细化与延伸.
教材分析与处理
教学设计的理念
教学程序的设计
教学方式的构建
掌握关于坐标轴(或关于直线x=m,y=n)对称的两个点的坐标之间的对应关系,会作出一个图形关于坐标轴对称的图形.
知识与技能
过程与方法
通过探究关于坐标轴对称的两个点坐标之间关系的活动,培养学生:作图--观察--猜想--验证--归纳这一研究数学问题的基本方法。
教学目标
教材分析与处理
通过探究活动,培养学生的 主动探究,合作交流的意识,体验探究的甘苦和成功的喜悦。
情感态度与价值观
教学重点与难点
掌握在平面直角坐标系中关于坐标轴对称的两个
点坐标之间的对应关系.
重点
用严密的数学语言归纳、表述关于坐标轴对称的两个点坐标之间的关系.并能在平面直角坐标系中作出轴对称图形.
难点
教材分析与处理
用坐标表示轴对称
教 法 分 析
结合学生的认知结构,年龄特征及本节课的特点,采用作图--观察--猜想--验证--归纳为主,多媒体演示为辅的教学方法, 在教学的过程中,设计带有启发性、思考性的问题 ,创设情境,引导学生独立思考,自主探索,合作交流,让学生始终处于一种积极思维、主动探究的学习状态.多媒体教学手段的使用增加了教学的直观性,趣味性,从而加大课堂容量、提高教学效率.
学 法 指 导
在本节课的教学中要帮助学生学会运用观察、分析、比较、归纳、概括等方法去解决问题 .使学习知识和培养能力融为一体.
教 学 手 段
采用多媒体课件及教学材料(方格纸)辅助教学.
教学设计的理念
教学程序的设计
教材分析与处理
教学方式的构建
用坐标表示轴对称
引入新课
创设情境
探索新知
动手实践
思维升华
探究拓展
巩固新知
尝试运用
反思评价
体验收获
课堂延伸
布置作业
教学程序的设计
教学设计的理念
教材分析与处理
教学方式的构建
板书设计
创设情境,引入新课
老北京的地图中,其中西直门和东直门是关于中轴线对称的,如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系, 对应于如图所示的东直门的坐标, 你能找到西直门的位置,说出西直门的坐标吗
右安门
左安门
广安门
广渠门
西便门
东便门
西直门
东直门
阜成门
朝阳门
德胜门
安定门
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
y
永定门
天安门
O
引入新课
创设情境
探索新知
动手实践
提升思维
拓展探究
知识升华
实践应用
课堂延伸
布置作业
板书设计
教学程序的设计
反思评价
体验收获
动手实践,探索新知
在平面直角坐标系上作任意两点.
(1)作出它们关于y轴对称的点,标出点的坐标,填在表格上.
(2) 探究关于y轴对称的点坐标之间的关系,并用数学语言表达出来.
活动一
关于y轴对称 1 2 3 4 5 6 7 8
点
(x1,y1)
对称点(x2,y2)
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A
·
A1 (-2,3)
动手实践,探索新知
y
x
(2,3)
·
动手实践,探索新知
探究结论
关于y 轴对称的点纵坐标相同, 横坐标互为相反数.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
动手实践,探索新知
y
x
(-2,3)
A2
·
(2,3)
A
·
动手实践,探索新知
探究结论
关于y 轴对称的点纵坐标相同,横坐标互为相反数.
关于x轴对称的点横坐标相同,纵坐标互为相反数.
关于哪个轴对称,哪个坐标就不变,另一个坐标互为相反数.
动手实践,探索新知
说出下列各点关于x轴、y轴对称的点的坐标:
(1,3) (-2,6) (-4,-2)
(1,0) (1,-2) (0,-5)
习 题
动手实践,探索新知
在平面直角坐标系上作任意两点A和B,连接AB,再作出A,B两点关于x轴对称的点A1,B1,连接A1,B1 ,你有怎样的发现 关于y轴呢?
活动二
动手实践,探索新知
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
·
·
·
A
B
A1
B1
·
·
C(2,2 )
C1 (2,-2 )
y
x
·
·
A2
B2
·
C2(-2,2 )
动手实践,探索新知
如图,四边形ABCD的四个顶点的坐标分别为A(-5 ,1)、B(-2 , 1)、C(-2 ,5)、D(-5 ,4),分别作出四边形ABCD关于x轴、y轴对称的图形.
活动三
动手实践,探索新知
学习目标
能求出一个点关于坐标轴对称的点的坐标;
能作出一个图形关于坐标轴对称的图形。
引入新课
创设情境
探索新知
动手实践
思维升华
探究拓展
巩固新知
尝试运用
课堂延伸
布置作业
板书设计
教学程序的设计
反思评价
体验收获
拓展探究,提升思维
活动四
如图所示,分别作出△PQR关于直线x=1和直线y=-1对称的图形.
-1
-2
-3
-4
-5
-6
-7
x
y
X=1
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1 0
7
6
5
4
3
2
1
x
y
y=-1
Q
探究拓展,思维升华
探究拓展,思维升华
探究结论
点A(x ,y)
关于直线x=m对称的
点A1的坐标是(x1,y1)
点A(x ,y)
关于直线y=n对称的
点A2的坐标是(x2,y2)
探究拓展,思维升华
探究结论
点A及A1的坐标满足:
(1) x1-m=m-x ;即x1=2m-x
(2) y1 = y
点A(x ,y)关于直线x=m对称
的点A1的坐标是(2m-x,y)
点A及A2的坐标满足:
(1) y2-n = n-y ;即y2=2n-y
(2) x2 = x
点A(x ,y)关于直线y=n对称的
点A2的坐标是(x ,2n-y)
习 题
探究拓展,思维升华
(1)点(-2,-3)关于直线x=-1 的对称点的坐标为 ; 关于直线y=2 的对称点的坐标为 .
(2)点(2,4)与点(4,4)是关于直线 对称的.
引入新课
创设情境
探索新知
动手实践
思维升华
探究拓展
巩固新知
尝试运用
课堂延伸
布置作业
板书设计
教学程序的设计
反思评价
体验收获
尝试运用,巩固新知
(1)若点M(2,a)和点N(a+b,-3)关于x轴对称,试求a,b的值;若这两个点关于y轴对称呢?
(2)已知长方形ABCD关于y轴对称,平行于y轴的边AB长是6,点A的坐标是(-2,-1),请你写出B、C、D三点的坐标.
(3)已知点的坐标A(2,2),B(1,1),C(3,-1.5),D(3,2).请写出A、B两点关于CD对称的点E、F的坐标,并在图中画出这两点.
(4)在坐标系中描出点A(-1,3),B(5,-4),c(-3,-1),D(-1,1),E(-3,5),F(5,8),连接AB,BC,AC,DE,EF,DF,请你判断所得的图形是轴对称图形吗 如果不是,请说明理由,如果是,请说出对称轴.
引入新课
创设情境
探索新知
动手实践
思维升华
探究拓展
巩固新知
尝试运用
课堂延伸
布置作业
板书设计
教学程序的设计
反思评价
体验收获
体验收获,反思评价
知识点
感受
问题
本节课你有哪些收获?
引入新课
创设情境
探索新知
动手实践
思维升华
探究拓展
巩固新知
尝试运用
课堂延伸
布置作业
板书设计
教学程序的设计
反思评价
体验收获
将点(2,1),(5,1),(2,5)做如下变化:
①纵坐标不变,横坐标分别加2.②横坐标不变,纵坐标分别加1.③纵坐标不变,横坐标分别变为原来的2倍.④横坐标不变,纵坐标分别变为原来的2倍.⑤纵坐标不变,横坐标分别乘以-1.⑥横坐标不变,纵坐标分别乘以-1.⑦纵坐标、横都分别乘以-1.
观察变化后的三角形与原三角形有什么变化,并用语言描述出来.
必做题:
布置作业,课堂延伸
选做题:
你能利用本节课的探究的方法,找出一个点关于直线y=x和y=-x对称的点的坐标吗
引入新课
创设情境
探索新知
动手实践
思维升华
探究拓展
巩固新知
尝试运用
课堂延伸
布置作业
板书设计
教学程序的设计
反思评价
体验收获
19.2.2 用坐标表示轴对称
在平面直角坐标系中:
点(x, y)关于x轴对称的点的坐标为(x,-y).
关于y轴对称的点的坐标为(-x, y).
关于直线x=m对称的点的坐标为(2m-x, y)
关于直线y=n对称的点的坐标为(x, 2n- y)
板书设计
