第七章《平行线的证明》检测试卷A(含答案)
文档属性
| 名称 | 第七章《平行线的证明》检测试卷A(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 22:07:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版2021-20202年八年级(上)第七章平行线的证明检测试卷A
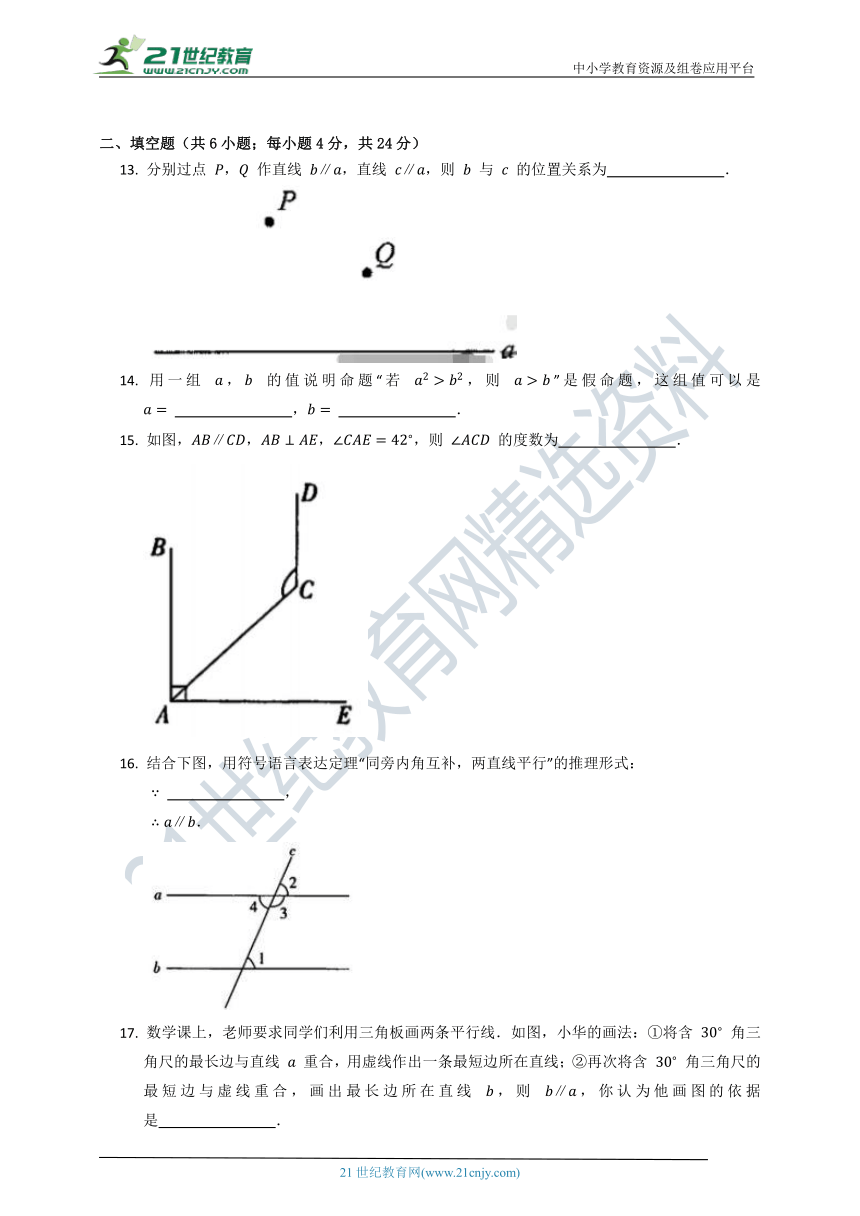
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 如图,,, 的大小关系是
A. B. C. D.
2. 能说明“锐角 ,锐角 的和是锐角”是假命题的例证图是
A. B.
C. D.
3. 如图,直线 , 被直线 所截,,且 ,则
A. B. C. D.
4. 如图,点 在 的延长线上,下列条件中能判断 的是
A. B.
C. D.
5. 小明放学回家自己煮面条吃,有下面几道工序:()洗锅盛水 分钟;()洗菜 分钟;()准备面条及佐料 分钟;()把水烧开 分钟;()用烧开的水煮面条和菜要 分钟.以上各工序除()外,一次只能进行一道工序,小明要将面条煮好,最少用
A. 分钟 B. 分钟 C. 分钟 D. 分钟
6. 如图,直线 , 被直线 所截,,,则
A. B. C. D.
7. 甲、乙、丙、丁四个小朋友在院里玩球,忽听“砰”的一声,球击中了李大爷家的窗户.李大爷跑出来察看,发现一块窗户玻璃被打碎了.李大爷问:“是谁闯的祸 ”
甲说:“是乙不小心闯的祸.”
乙说:“是丙闯的祸.”
丙说:“乙说的不是实话.”
丁说:“反正不是我闯的祸.”
如果这四个小朋友中只有一个人说了实话,请你帮李大爷判断一下,究竟是谁闯的祸
A. 甲 B. 乙 C. 丙 D. 丁
8. 如图,下列条件中,能判定直线 的是
A. B. C. D.
9. 如图, 是 的外角,若 ,,则
A. B. C. D.
10. 如图, 处在 处的北偏东 方向, 处在 处的北偏西 方向,则 等于
A. B. C. D.
11. 下列命题是真命题的是
A. 两边及其中一边的对角分别相等的两个三角形全等
B. 平分弦的直径垂直于弦
C. 一组对边平行且一组对角相等的四边形是平行四边形
D. 两条直线被第三条直线所截,内错角相等
12. 下列命题中是真命题的是
A. 同位角相等
B. 有两边及一角分别相等的两个三角形全等
C. 两组对边分别相等的四边形是平行四边形
D. 垂直于半径的直线是圆的切线
二、填空题(共6小题;每小题4分,共24分)
13. 分别过点 , 作直线 ,直线 ,则 与 的位置关系为 .
14. 用一组 , 的值说明命题“若 ,则 ”是假命题,这组值可以是 , .
15. 如图,,,,则 的度数为 .
16. 结合下图,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:
,
.
17. 数学课上,老师要求同学们利用三角板画两条平行线.如图,小华的画法:①将含 角三角尺的最长边与直线 重合,用虚线作出一条最短边所在直线;②再次将含 角三角尺的最短边与虚线重合,画出最长边所在直线 ,则 ,你认为他画图的依据是 .
18. 下图是某剧场第一排座位分布图.甲、乙、丙、丁四人购票,所购票数分别为 ,,,.每人选座购票时,只购买第一排的座位相邻的票,同时使自己所选的座位号之和最小.如果按“甲、乙、丙、丁”的先后顺序购票,那么甲购买 , 号座位的票,乙购买 ,, 号座位的票,丙选座购票后,丁无法购买到第一排座位的票.若丙第一个购票,要使其他三人都能购买到第一排座位的票,写出一种满足条件的购票的先后顺序 .
三、解答题(共7小题;共60分)
19. (8分)如图所示,在同一平面内有直线 ,,,现有三个条件:
① ;
② ;
③ .
请以其中两个为条件,另一个为结论构造命题.
(1)请写出你构造的所有命题.
(2)你构造的命题哪些是真命题,哪些是假命题 若是假命题,请举反例说明.
20. (8分)写出下列命题的已知、求证,并完成证明过程.命题:在同一平面内,垂直于同一条直线的两条直线互相平行.
已知:如图, .
求证: .
然后给出证明.
21. (8分)如图,已知 , 平分 ,且 ,.
(1)求 的度数;
(2)求 的度数.
22. (8分)用语言叙述下列命题.
如图,已知 ,直线 交 于 ,交 于 , 平分 , 平分 ,则 .
23. (8分)某次足球比赛的规则如下:四个球队进行单循环比赛(每两队赛一场),胜一场得 分,平一场得 分,负一场得 分,某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙队打平的是哪几个球队
24. (10分)下面是小明设计的“过直线外一点作这条直线的平行线”的尺规作图过程.已知:如图,直线 及直线 外一点 .
求作:直线 ,使得 .
作法:如图,
①在直线 上取一点 ,连接 ;
②作 的平分线 ;
③以点 为圆心, 长为半径画弧,交射线 于点 ;
④作直线 .
所以直线 就是所求作的直线.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明: 平分 ,
.
,
.
.
.( )(填推理的依据)
25.(10分) 如图①, 是 的外角, 平分 , 平分 ,且 , 交于点 .
(1)若 ,,则 .
(2) 与 有什么数量关系 (直接写出结论)
(3)如图②,点 是 两外角平分线 , 的交点,探索 与 之间的数量关系.
答案
第一部分
1. B
2. C 【解析】C选项中,三角形三个内角都是锐角,
所以 .
3. B 【解析】 ,
.
,
.
.
4. A
5. C
【解析】第一步,洗锅盛水 分钟;第二步,把水烧开 分钟,同时洗菜 分钟,准备面条及佐料 分钟,总计 分钟;第三步,用烧开的水煮面条和菜要 分钟.故共用 分钟.
6. B 【解析】,,
.
7. D 【解析】本题可分三种情况进行讨论:
①若甲真,则乙假,丙真,丁真,这种情况下,三人说了实话,显然与题意不符;
②若甲假,乙真,则丙假,丁真,这种情况下,两人说了实话,显然与题意不符;
③若甲假,乙假,则丙真,丁可能真也可能假,当丁真时,两人说了实话,显然与条件不符,故丁假,这种情况下,只有丙说了实话,符合题目给出的条件.
由于丁说了假话,因此闯祸的人一定是丁.
故选D.
8. C 【解析】 和 是 和 被 所截形成的同旁内角,若它们互补,则 与 平行.
9. D
10. D
【解析】过点 作 与正北方向平行,交 于点 ,则 ,.
,
故选D.
11. C 【解析】【分析】、根据全等三角形的判定方法,判断即可.
、根据垂径定理的推理对进行判断;
、根据平行四边形的判定进行判断;
、根据平行线的判定进行判断.
【解析】解:、由两边及其中一边的对角分别相等无法证明两个三角形全等,故错误,是假命题;
、平分弦非直径的直径垂直于弦,故错误,是假命题;
、一组对边平行且一组对角相等的四边形是平行四边形,故正确,是真命题;
、两条平行线被第三条直线所截,内错角相等,故错误,是假命题;
故选:.
【点评】本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,有些命题的正确性是用推理证实的,这样的真命题叫做定理.
12. C 【解析】【分析】根据平行线的性质对进行判断;根据三角形全等的判定方法对进行判断;根据平行线的判定对进行判断;根据切线的判定对进行判断.
【解析】解:、两直线平行,同位角相等,故错误;
、两边和夹角相等的两个三角形全等,故错误;
、两组对边分别相等的四边形是平行四边形,故正确;
、垂直于半径且过半径的外端点的直线是圆的切线,故错误.
故选:.
【点评】本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果那么”形式;有些命题的正确性是用推理证实的,这样的真命题叫做定理.
第二部分
13.
14. ,(答案不唯一)
【解析】当 , 时,,,
此时 ,而 ,
命题“若 ,则 ”是假命题.
15.
【解析】,
,
,,
.
.
16.
【解析】 与 是直线 和 被直线 所截形成的同旁内角.
17. 内错角相等,两直线平行
18. 答案不唯一,如:丙、丁、甲、乙
【解析】已知丙第一个购票,且买 张,可知丙购买的是 ,,, 这四个位置,则左边剩余 个位置,右边剩余 个位置;
若甲第二个购票,则甲购买的是 , 这两个位置,此时只能是丁第三个购票,乙最后购票,否则无法满足题意,即此时顺序为丙、甲、丁、乙;
同理,若乙第二个购票,则乙购买的是 ,, 这三个位置,接下来只能是丁第三个,甲第四个,即此时顺序为丙、乙、丁、甲;
若丁第二个购票,则甲、乙顺序无影响,即此时顺序为丙、丁、甲、乙(或丙、丁、乙、甲).
第三部分
19. (1) 命题 :若 ,,则 .
命题 :若 ,,则 .
命题 :若 ,,则 .
(2) 三个命题都是真命题.
20. ,垂足为 ,,垂足为 ;
,,
,
.
21. (1) ,
.
(2) ,
,
平分 ,
,
,
,
.
22. 两条平行直线被第三条直线所截,一对同旁内角的角平分线互相垂直.
23. 因为甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,
所以甲队得 分, 胜 平;乙队得 分, 胜 平;丙队得 分, 胜 平;丁队得 分, 胜 平.
因为甲、乙两队都没有输球,所以甲队一定与乙队平.
因为乙队得 分, 胜 平,丁队得 分, 胜 平,
所以与乙队打平的球队是甲队与丁队.
24. (1)
(2) ;;内错角相等,两直线平行
25. (1)
(2) .
(3) , 是 两外角的平分线,
,.
,,
,.
,
,
即 .
又 ,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版2021-20202年八年级(上)第七章平行线的证明检测试卷A
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 如图,,, 的大小关系是
A. B. C. D.
2. 能说明“锐角 ,锐角 的和是锐角”是假命题的例证图是
A. B.
C. D.
3. 如图,直线 , 被直线 所截,,且 ,则
A. B. C. D.
4. 如图,点 在 的延长线上,下列条件中能判断 的是
A. B.
C. D.
5. 小明放学回家自己煮面条吃,有下面几道工序:()洗锅盛水 分钟;()洗菜 分钟;()准备面条及佐料 分钟;()把水烧开 分钟;()用烧开的水煮面条和菜要 分钟.以上各工序除()外,一次只能进行一道工序,小明要将面条煮好,最少用
A. 分钟 B. 分钟 C. 分钟 D. 分钟
6. 如图,直线 , 被直线 所截,,,则
A. B. C. D.
7. 甲、乙、丙、丁四个小朋友在院里玩球,忽听“砰”的一声,球击中了李大爷家的窗户.李大爷跑出来察看,发现一块窗户玻璃被打碎了.李大爷问:“是谁闯的祸 ”
甲说:“是乙不小心闯的祸.”
乙说:“是丙闯的祸.”
丙说:“乙说的不是实话.”
丁说:“反正不是我闯的祸.”
如果这四个小朋友中只有一个人说了实话,请你帮李大爷判断一下,究竟是谁闯的祸
A. 甲 B. 乙 C. 丙 D. 丁
8. 如图,下列条件中,能判定直线 的是
A. B. C. D.
9. 如图, 是 的外角,若 ,,则
A. B. C. D.
10. 如图, 处在 处的北偏东 方向, 处在 处的北偏西 方向,则 等于
A. B. C. D.
11. 下列命题是真命题的是
A. 两边及其中一边的对角分别相等的两个三角形全等
B. 平分弦的直径垂直于弦
C. 一组对边平行且一组对角相等的四边形是平行四边形
D. 两条直线被第三条直线所截,内错角相等
12. 下列命题中是真命题的是
A. 同位角相等
B. 有两边及一角分别相等的两个三角形全等
C. 两组对边分别相等的四边形是平行四边形
D. 垂直于半径的直线是圆的切线
二、填空题(共6小题;每小题4分,共24分)
13. 分别过点 , 作直线 ,直线 ,则 与 的位置关系为 .
14. 用一组 , 的值说明命题“若 ,则 ”是假命题,这组值可以是 , .
15. 如图,,,,则 的度数为 .
16. 结合下图,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:
,
.
17. 数学课上,老师要求同学们利用三角板画两条平行线.如图,小华的画法:①将含 角三角尺的最长边与直线 重合,用虚线作出一条最短边所在直线;②再次将含 角三角尺的最短边与虚线重合,画出最长边所在直线 ,则 ,你认为他画图的依据是 .
18. 下图是某剧场第一排座位分布图.甲、乙、丙、丁四人购票,所购票数分别为 ,,,.每人选座购票时,只购买第一排的座位相邻的票,同时使自己所选的座位号之和最小.如果按“甲、乙、丙、丁”的先后顺序购票,那么甲购买 , 号座位的票,乙购买 ,, 号座位的票,丙选座购票后,丁无法购买到第一排座位的票.若丙第一个购票,要使其他三人都能购买到第一排座位的票,写出一种满足条件的购票的先后顺序 .
三、解答题(共7小题;共60分)
19. (8分)如图所示,在同一平面内有直线 ,,,现有三个条件:
① ;
② ;
③ .
请以其中两个为条件,另一个为结论构造命题.
(1)请写出你构造的所有命题.
(2)你构造的命题哪些是真命题,哪些是假命题 若是假命题,请举反例说明.
20. (8分)写出下列命题的已知、求证,并完成证明过程.命题:在同一平面内,垂直于同一条直线的两条直线互相平行.
已知:如图, .
求证: .
然后给出证明.
21. (8分)如图,已知 , 平分 ,且 ,.
(1)求 的度数;
(2)求 的度数.
22. (8分)用语言叙述下列命题.
如图,已知 ,直线 交 于 ,交 于 , 平分 , 平分 ,则 .
23. (8分)某次足球比赛的规则如下:四个球队进行单循环比赛(每两队赛一场),胜一场得 分,平一场得 分,负一场得 分,某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙队打平的是哪几个球队
24. (10分)下面是小明设计的“过直线外一点作这条直线的平行线”的尺规作图过程.已知:如图,直线 及直线 外一点 .
求作:直线 ,使得 .
作法:如图,
①在直线 上取一点 ,连接 ;
②作 的平分线 ;
③以点 为圆心, 长为半径画弧,交射线 于点 ;
④作直线 .
所以直线 就是所求作的直线.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明: 平分 ,
.
,
.
.
.( )(填推理的依据)
25.(10分) 如图①, 是 的外角, 平分 , 平分 ,且 , 交于点 .
(1)若 ,,则 .
(2) 与 有什么数量关系 (直接写出结论)
(3)如图②,点 是 两外角平分线 , 的交点,探索 与 之间的数量关系.
答案
第一部分
1. B
2. C 【解析】C选项中,三角形三个内角都是锐角,
所以 .
3. B 【解析】 ,
.
,
.
.
4. A
5. C
【解析】第一步,洗锅盛水 分钟;第二步,把水烧开 分钟,同时洗菜 分钟,准备面条及佐料 分钟,总计 分钟;第三步,用烧开的水煮面条和菜要 分钟.故共用 分钟.
6. B 【解析】,,
.
7. D 【解析】本题可分三种情况进行讨论:
①若甲真,则乙假,丙真,丁真,这种情况下,三人说了实话,显然与题意不符;
②若甲假,乙真,则丙假,丁真,这种情况下,两人说了实话,显然与题意不符;
③若甲假,乙假,则丙真,丁可能真也可能假,当丁真时,两人说了实话,显然与条件不符,故丁假,这种情况下,只有丙说了实话,符合题目给出的条件.
由于丁说了假话,因此闯祸的人一定是丁.
故选D.
8. C 【解析】 和 是 和 被 所截形成的同旁内角,若它们互补,则 与 平行.
9. D
10. D
【解析】过点 作 与正北方向平行,交 于点 ,则 ,.
,
故选D.
11. C 【解析】【分析】、根据全等三角形的判定方法,判断即可.
【解析】解:、由两边及其中一边的对角分别相等无法证明两个三角形全等,故错误,是假命题;
故选:.
【点评】本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,有些命题的正确性是用推理证实的,这样的真命题叫做定理.
12. C 【解析】【分析】根据平行线的性质对进行判断;根据三角形全等的判定方法对进行判断;根据平行线的判定对进行判断;根据切线的判定对进行判断.
【解析】解:、两直线平行,同位角相等,故错误;
、两边和夹角相等的两个三角形全等,故错误;
、两组对边分别相等的四边形是平行四边形,故正确;
、垂直于半径且过半径的外端点的直线是圆的切线,故错误.
故选:.
【点评】本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果那么”形式;有些命题的正确性是用推理证实的,这样的真命题叫做定理.
第二部分
13.
14. ,(答案不唯一)
【解析】当 , 时,,,
此时 ,而 ,
命题“若 ,则 ”是假命题.
15.
【解析】,
,
,,
.
.
16.
【解析】 与 是直线 和 被直线 所截形成的同旁内角.
17. 内错角相等,两直线平行
18. 答案不唯一,如:丙、丁、甲、乙
【解析】已知丙第一个购票,且买 张,可知丙购买的是 ,,, 这四个位置,则左边剩余 个位置,右边剩余 个位置;
若甲第二个购票,则甲购买的是 , 这两个位置,此时只能是丁第三个购票,乙最后购票,否则无法满足题意,即此时顺序为丙、甲、丁、乙;
同理,若乙第二个购票,则乙购买的是 ,, 这三个位置,接下来只能是丁第三个,甲第四个,即此时顺序为丙、乙、丁、甲;
若丁第二个购票,则甲、乙顺序无影响,即此时顺序为丙、丁、甲、乙(或丙、丁、乙、甲).
第三部分
19. (1) 命题 :若 ,,则 .
命题 :若 ,,则 .
命题 :若 ,,则 .
(2) 三个命题都是真命题.
20. ,垂足为 ,,垂足为 ;
,,
,
.
21. (1) ,
.
(2) ,
,
平分 ,
,
,
,
.
22. 两条平行直线被第三条直线所截,一对同旁内角的角平分线互相垂直.
23. 因为甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,
所以甲队得 分, 胜 平;乙队得 分, 胜 平;丙队得 分, 胜 平;丁队得 分, 胜 平.
因为甲、乙两队都没有输球,所以甲队一定与乙队平.
因为乙队得 分, 胜 平,丁队得 分, 胜 平,
所以与乙队打平的球队是甲队与丁队.
24. (1)
(2) ;;内错角相等,两直线平行
25. (1)
(2) .
(3) , 是 两外角的平分线,
,.
,,
,.
,
,
即 .
又 ,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
