第七章 平行线的证明 单元质量检测试卷B(含解析)
文档属性
| 名称 | 第七章 平行线的证明 单元质量检测试卷B(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
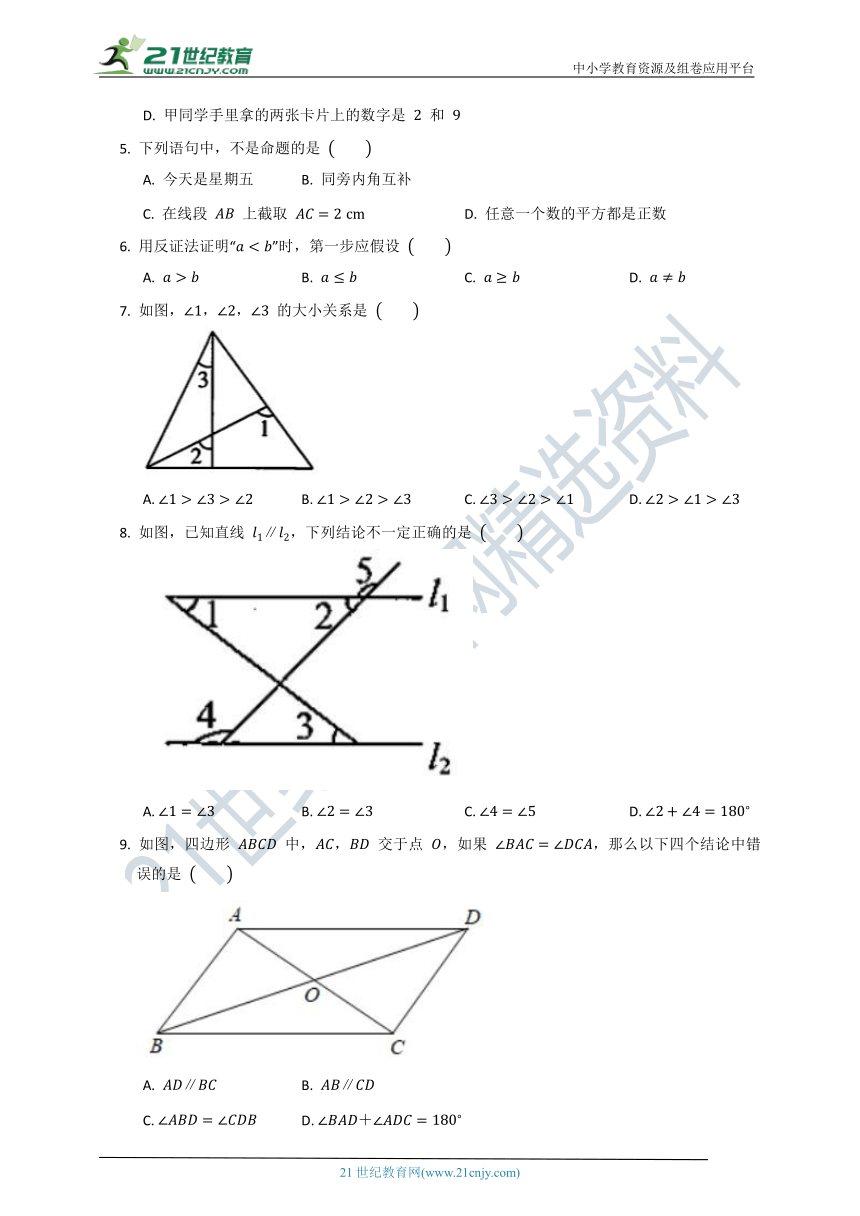
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 06:44:49 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
北师大版2021-2022学年八年级(上)第七章平行线的证明检测试卷B
(时间120分钟,满分120分)
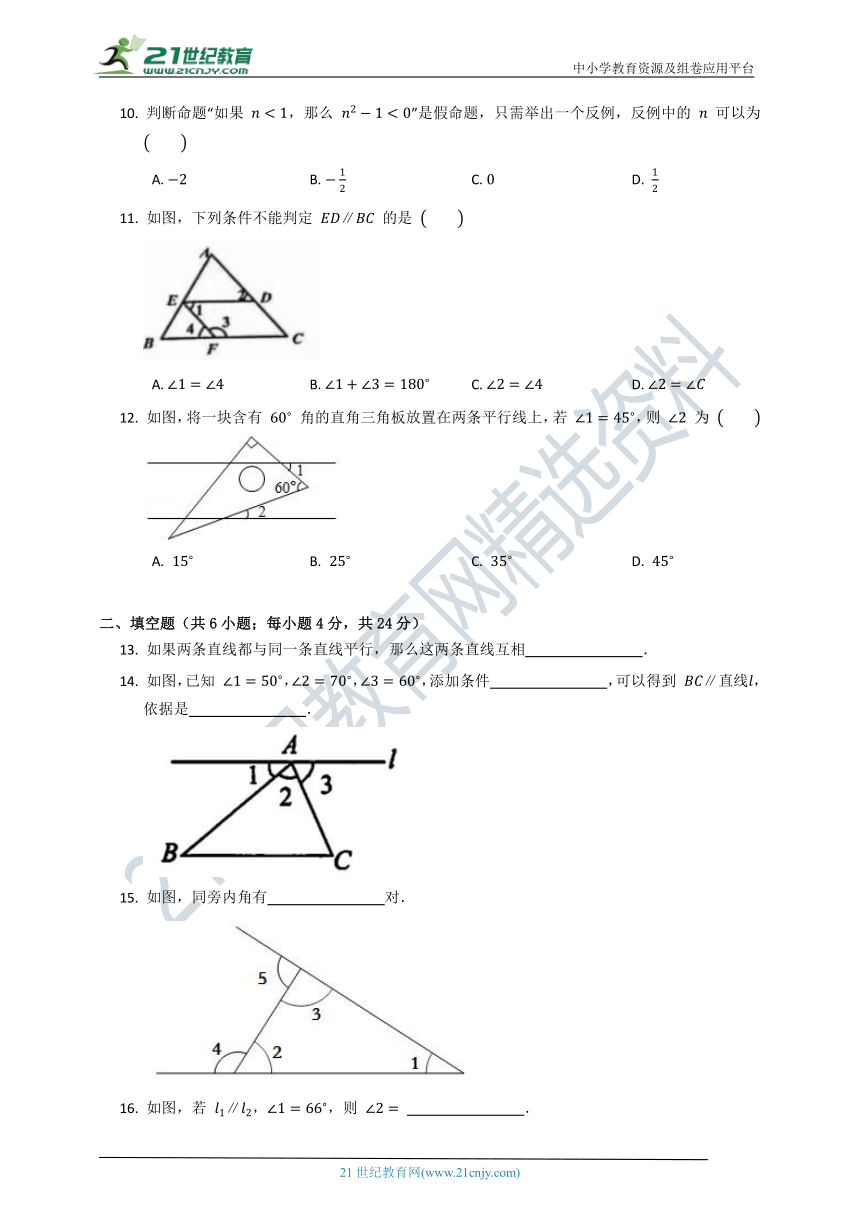
一、选择题(共12小题;每小题3分,共36分)
1. 如图所示,点 在 的延长线上,下列条件中能判断
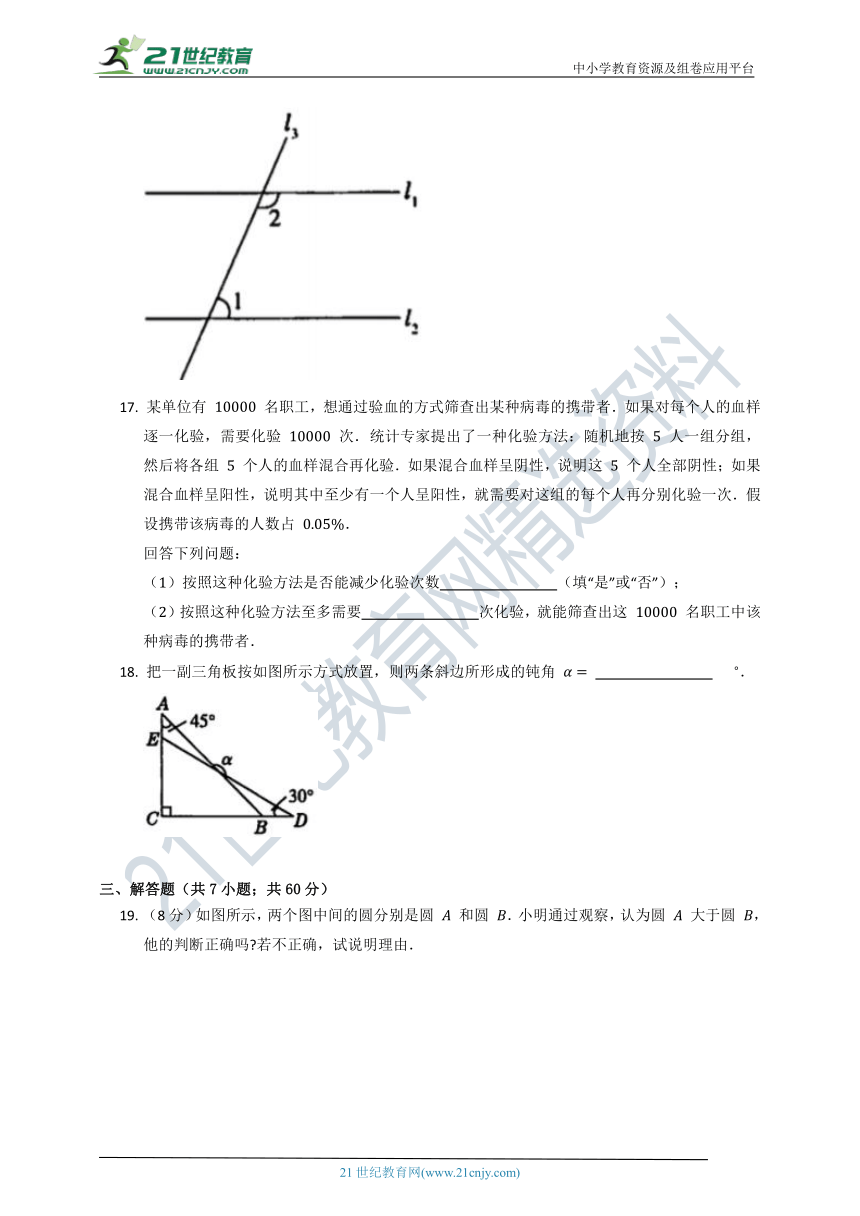
A. B.
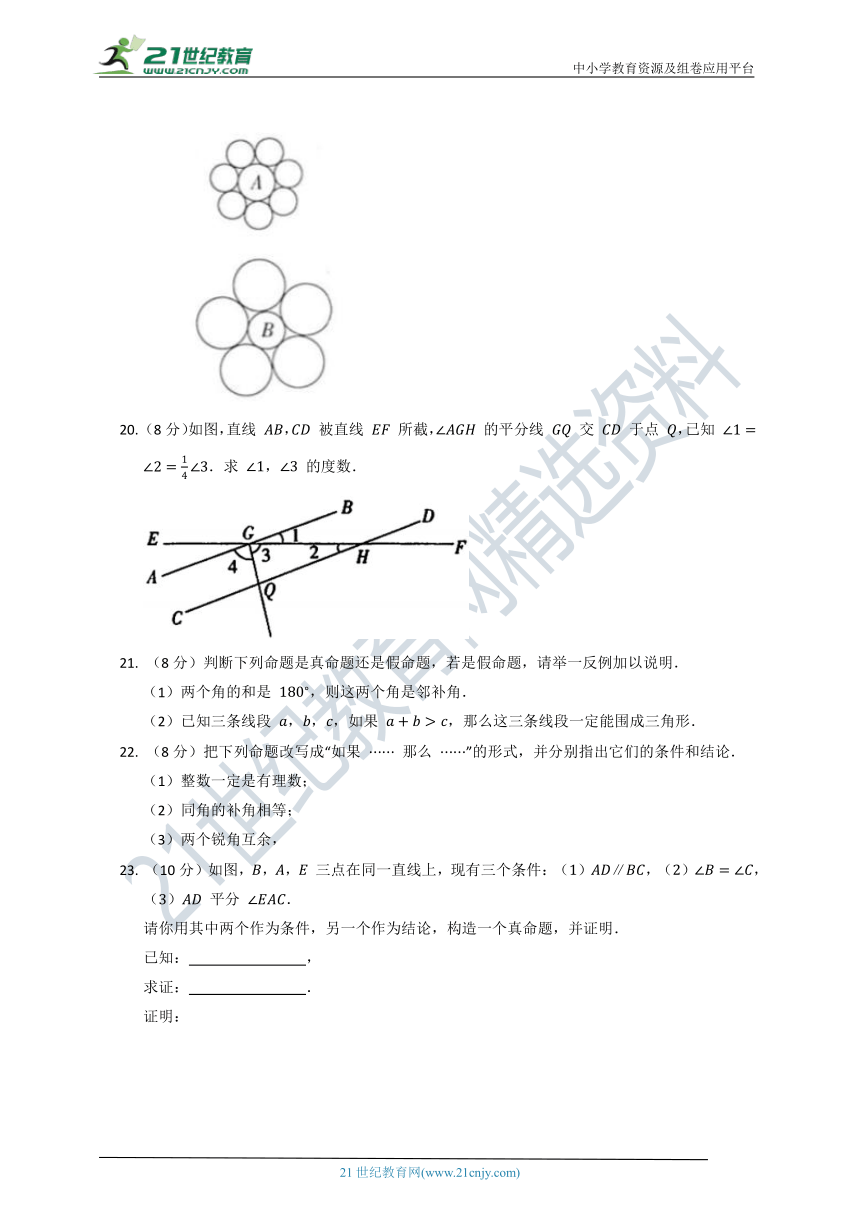
C. D.
2. 下列命题中,是假命题的是
A. 平面内,若 ,,那么
B. 两直线平行,同位角相等
C. 负数的平方根是负数
D. 若 ,则
3. 如图,已知 ,要使 ,则需具备的另一个条件为
A. B. C. D.
4. 在一次数学活动课上,某数学老师将 共十个整数依次写在十张不透明的卡片上(每张卡片上只写一个数字,每一个数字只写在一张卡片上,而且把写有数字的那一面朝下).他先像洗扑克牌一样打乱这些卡片的顺序,然后把甲,乙,丙,丁,戊五位同学叫到讲台上,随机地发给每位同学两张卡片,并要求他们把自己手里拿的两张卡片上的数字之和写在黑板上,写出的结果依次是:甲:;乙:;丙:;丁:;戊:.根据以上信息,下列判断正确的是
A. 戊同学手里拿的两张卡片上的数字是 和
B. 丙同学手里拿的两张卡片上的数字是 和
C. 丁同学手里拿的两张卡片上的数字是 和
D. 甲同学手里拿的两张卡片上的数字是 和
5. 下列语句中,不是命题的是
A. 今天是星期五 B. 同旁内角互补
C. 在线段 上截取 D. 任意一个数的平方都是正数
6. 用反证法证明“”时,第一步应假设
A. B. C. D.
7. 如图,,, 的大小关系是
A. B. C. D.
8. 如图,已知直线 ,下列结论不一定正确的是
A. B. C. D.
9. 如图,四边形 中,, 交于点 ,如果 ,那么以下四个结论中错误的是
A. B.
C. D.
10. 判断命题“如果 ,那么 ”是假命题,只需举出一个反例,反例中的 可以为
A. B. C. D.
11. 如图,下列条件不能判定 的是
A. B. C. D.
12. 如图,将一块含有 角的直角三角板放置在两条平行线上,若 ,则 为
A. B. C. D.
二、填空题(共6小题;每小题4分,共24分)
13. 如果两条直线都与同一条直线平行,那么这两条直线互相 .
14. 如图,已知 ,,,添加条件 ,可以得到 ,依据是 .
15. 如图,同旁内角有 对.
16. 如图,若 ,,则 .
17. 某单位有 名职工,想通过验血的方式筛查出某种病毒的携带者.如果对每个人的血样逐一化验,需要化验 次.统计专家提出了一种化验方法:随机地按 人一组分组,然后将各组 个人的血样混合再化验.如果混合血样呈阴性,说明这 个人全部阴性;如果混合血样呈阳性,说明其中至少有一个人呈阳性,就需要对这组的每个人再分别化验一次.假设携带该病毒的人数占 .
回答下列问题:
()按照这种化验方法是否能减少化验次数 (填“是”或“否”);
()按照这种化验方法至多需要 次化验,就能筛查出这 名职工中该种病毒的携带者.
18. 把一副三角板按如图所示方式放置,则两条斜边所形成的钝角 .
三、解答题(共7小题;共60分)
19. (8分)如图所示,两个图中间的圆分别是圆 和圆 .小明通过观察,认为圆 大于圆 ,他的判断正确吗 若不正确,试说明理由.
20. (8分)如图,直线 , 被直线 所截, 的平分线 交 于点 ,已知 .求 , 的度数.
21. (8分)判断下列命题是真命题还是假命题,若是假命题,请举一反例加以说明.
(1)两个角的和是 ,则这两个角是邻补角.
(2)已知三条线段 ,,,如果 ,那么这三条线段一定能围成三角形.
22. (8分)把下列命题改写成“如果 那么 ”的形式,并分别指出它们的条件和结论.
(1)整数一定是有理数;
(2)同角的补角相等;
(3)两个锐角互余,
23. (10分)如图,,, 三点在同一直线上,现有三个条件:(),(),() 平分 .
请你用其中两个作为条件,另一个作为结论,构造一个真命题,并证明.
已知: ,
求证: .
证明:
24. (8分)如图,已知 ,,垂足分别为 ,,.
求证:.
25.(10分)如图所示,直线 ,直线 与 , 分别交于 , 两点,点 是线段 上的一个动点(不与 , 重合),试判断 ,, 这三个角之间有怎样的数量关系.先用量角器量一量,得出你的猜想,再证明.
答案
第一部分
1. A 【解析】A、根据内错角相等,两直线平行可得 ,故此选项正确;
B、根据内错角相等,两直线平行可得 ,故此选项错误;
C、根据内错角相等,两直线平行可得 ,故此选项错误;
D、根据同旁内角互补,两直线平行可得 ,故此选项错误;
故选:A.
2. C
3. C 【解析】若 ,则么 ,
(同旁内角互补,两直线平行).
故选C.
4. A 【解析】由题意可知,一共十张卡片十个数,五个人每人两张卡片,
每人手里的数字不重复.
由甲:,可知甲手中的数字可能是 和 , 和 , 和 , 和 , 和 ;
由乙:,可知乙手中的数字只有 和 ;
由丙:,可知丙手中的数字可能是 和 , 和 ;
由丁:,可知丁手中的数字可能是 和 , 和 , 和 ;
由戊:,可知戊手中的数字可能是 和 , 和 ;
丁只能是 和 ,甲只能是 和 ,丙只能是 和 ,戊只能是 和 .
各选项中,只有A是正确的.
5. C
【解析】A中“是”表示判断,是命题;
B中对同旁内角的数量关系作出判断,是命题,且是一个错误的命题,即假命题;
C只是表示一种动作,所以不是命题;
D中“都是”表示判断,是命题.
6. C 【解析】在反证法的步骤中,第一步是假设结论不成立,因此可假设 .
故选C.
7. B
8. B
9. A 【解析】,
,选项B正确;
,,选项C,D均正确;
根据已知条件无法证出 ,选项A错误;
故选:A.
10. A
【解析】当 时,满足 ,但 ,
所以判断命题“如果 ,那么 ”是假命题,可令 .
11. C
12. A 【解析】过三角形的 角的顶点 作 ,
,
,
,
,
,
.
第二部分
13. 平行
14. 答案不唯一,如 ,内错角相等,两直线平行
15.
16.
【解析】,
,
,
.
17. 是,
【解析】()是,
次 次,明显减少;
() 人,
故有 人是携带者,
第一轮: 次,
至多化验次数,故而这 个人都在不同组,
这样次数最多,
第二轮有 个组需要化验,
次,
次,
故至多需要 次化验.
18.
【解析】利用“三角形的一个外角等于与它不相邻的两个内角的和”来求解,即 .
第三部分
19. 小明的判断不正确.借助圆规或刻度尺可知两圆的半径或直径相等,故两圆一样大,小明的判断不正确.
20. 的平分线 交 于点 ,
,
,
,
,
,,
,
,
.
21. (1) 假命题.
如图所示,
在等腰 中,,,
则 ,但 与 不是邻补角.
(2) 假命题.
例如 ,,,,但 ,构不成三角形.
22. (1) 如果一个数是整数,那么它一定是有理数.
条件:一个数是整数;
结论:它一定是有理数.
(2) 如果两个角是同一个角的补角,那么这两个角相等.
条件:两个角是同一个角的补角;
结论:这两个角相等.
(3) 如果两个角是锐角,那么这两个角互为余角.
条件:两个角是锐角;
结论:这两个角互为余角.
23. ,; 平分
因为 ,
所以 ,.
又因为 ,
所以 ,
即 平分 .(答案不唯一)
24. ,,
,
,
.
,
,
.
25. 猜想:.
证明:如图所示,过点 作 ,
所以 (两直线平行,内错角相等).
因为 ,
所以 ,
所以 .
因为 ,
所以 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版2021-2022学年八年级(上)第七章平行线的证明检测试卷B
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 如图所示,点 在 的延长线上,下列条件中能判断
A. B.
C. D.
2. 下列命题中,是假命题的是
A. 平面内,若 ,,那么
B. 两直线平行,同位角相等
C. 负数的平方根是负数
D. 若 ,则
3. 如图,已知 ,要使 ,则需具备的另一个条件为
A. B. C. D.
4. 在一次数学活动课上,某数学老师将 共十个整数依次写在十张不透明的卡片上(每张卡片上只写一个数字,每一个数字只写在一张卡片上,而且把写有数字的那一面朝下).他先像洗扑克牌一样打乱这些卡片的顺序,然后把甲,乙,丙,丁,戊五位同学叫到讲台上,随机地发给每位同学两张卡片,并要求他们把自己手里拿的两张卡片上的数字之和写在黑板上,写出的结果依次是:甲:;乙:;丙:;丁:;戊:.根据以上信息,下列判断正确的是
A. 戊同学手里拿的两张卡片上的数字是 和
B. 丙同学手里拿的两张卡片上的数字是 和
C. 丁同学手里拿的两张卡片上的数字是 和
D. 甲同学手里拿的两张卡片上的数字是 和
5. 下列语句中,不是命题的是
A. 今天是星期五 B. 同旁内角互补
C. 在线段 上截取 D. 任意一个数的平方都是正数
6. 用反证法证明“”时,第一步应假设
A. B. C. D.
7. 如图,,, 的大小关系是
A. B. C. D.
8. 如图,已知直线 ,下列结论不一定正确的是
A. B. C. D.
9. 如图,四边形 中,, 交于点 ,如果 ,那么以下四个结论中错误的是
A. B.
C. D.
10. 判断命题“如果 ,那么 ”是假命题,只需举出一个反例,反例中的 可以为
A. B. C. D.
11. 如图,下列条件不能判定 的是
A. B. C. D.
12. 如图,将一块含有 角的直角三角板放置在两条平行线上,若 ,则 为
A. B. C. D.
二、填空题(共6小题;每小题4分,共24分)
13. 如果两条直线都与同一条直线平行,那么这两条直线互相 .
14. 如图,已知 ,,,添加条件 ,可以得到 ,依据是 .
15. 如图,同旁内角有 对.
16. 如图,若 ,,则 .
17. 某单位有 名职工,想通过验血的方式筛查出某种病毒的携带者.如果对每个人的血样逐一化验,需要化验 次.统计专家提出了一种化验方法:随机地按 人一组分组,然后将各组 个人的血样混合再化验.如果混合血样呈阴性,说明这 个人全部阴性;如果混合血样呈阳性,说明其中至少有一个人呈阳性,就需要对这组的每个人再分别化验一次.假设携带该病毒的人数占 .
回答下列问题:
()按照这种化验方法是否能减少化验次数 (填“是”或“否”);
()按照这种化验方法至多需要 次化验,就能筛查出这 名职工中该种病毒的携带者.
18. 把一副三角板按如图所示方式放置,则两条斜边所形成的钝角 .
三、解答题(共7小题;共60分)
19. (8分)如图所示,两个图中间的圆分别是圆 和圆 .小明通过观察,认为圆 大于圆 ,他的判断正确吗 若不正确,试说明理由.
20. (8分)如图,直线 , 被直线 所截, 的平分线 交 于点 ,已知 .求 , 的度数.
21. (8分)判断下列命题是真命题还是假命题,若是假命题,请举一反例加以说明.
(1)两个角的和是 ,则这两个角是邻补角.
(2)已知三条线段 ,,,如果 ,那么这三条线段一定能围成三角形.
22. (8分)把下列命题改写成“如果 那么 ”的形式,并分别指出它们的条件和结论.
(1)整数一定是有理数;
(2)同角的补角相等;
(3)两个锐角互余,
23. (10分)如图,,, 三点在同一直线上,现有三个条件:(),(),() 平分 .
请你用其中两个作为条件,另一个作为结论,构造一个真命题,并证明.
已知: ,
求证: .
证明:
24. (8分)如图,已知 ,,垂足分别为 ,,.
求证:.
25.(10分)如图所示,直线 ,直线 与 , 分别交于 , 两点,点 是线段 上的一个动点(不与 , 重合),试判断 ,, 这三个角之间有怎样的数量关系.先用量角器量一量,得出你的猜想,再证明.
答案
第一部分
1. A 【解析】A、根据内错角相等,两直线平行可得 ,故此选项正确;
B、根据内错角相等,两直线平行可得 ,故此选项错误;
C、根据内错角相等,两直线平行可得 ,故此选项错误;
D、根据同旁内角互补,两直线平行可得 ,故此选项错误;
故选:A.
2. C
3. C 【解析】若 ,则么 ,
(同旁内角互补,两直线平行).
故选C.
4. A 【解析】由题意可知,一共十张卡片十个数,五个人每人两张卡片,
每人手里的数字不重复.
由甲:,可知甲手中的数字可能是 和 , 和 , 和 , 和 , 和 ;
由乙:,可知乙手中的数字只有 和 ;
由丙:,可知丙手中的数字可能是 和 , 和 ;
由丁:,可知丁手中的数字可能是 和 , 和 , 和 ;
由戊:,可知戊手中的数字可能是 和 , 和 ;
丁只能是 和 ,甲只能是 和 ,丙只能是 和 ,戊只能是 和 .
各选项中,只有A是正确的.
5. C
【解析】A中“是”表示判断,是命题;
B中对同旁内角的数量关系作出判断,是命题,且是一个错误的命题,即假命题;
C只是表示一种动作,所以不是命题;
D中“都是”表示判断,是命题.
6. C 【解析】在反证法的步骤中,第一步是假设结论不成立,因此可假设 .
故选C.
7. B
8. B
9. A 【解析】,
,选项B正确;
,,选项C,D均正确;
根据已知条件无法证出 ,选项A错误;
故选:A.
10. A
【解析】当 时,满足 ,但 ,
所以判断命题“如果 ,那么 ”是假命题,可令 .
11. C
12. A 【解析】过三角形的 角的顶点 作 ,
,
,
,
,
,
.
第二部分
13. 平行
14. 答案不唯一,如 ,内错角相等,两直线平行
15.
16.
【解析】,
,
,
.
17. 是,
【解析】()是,
次 次,明显减少;
() 人,
故有 人是携带者,
第一轮: 次,
至多化验次数,故而这 个人都在不同组,
这样次数最多,
第二轮有 个组需要化验,
次,
次,
故至多需要 次化验.
18.
【解析】利用“三角形的一个外角等于与它不相邻的两个内角的和”来求解,即 .
第三部分
19. 小明的判断不正确.借助圆规或刻度尺可知两圆的半径或直径相等,故两圆一样大,小明的判断不正确.
20. 的平分线 交 于点 ,
,
,
,
,
,,
,
,
.
21. (1) 假命题.
如图所示,
在等腰 中,,,
则 ,但 与 不是邻补角.
(2) 假命题.
例如 ,,,,但 ,构不成三角形.
22. (1) 如果一个数是整数,那么它一定是有理数.
条件:一个数是整数;
结论:它一定是有理数.
(2) 如果两个角是同一个角的补角,那么这两个角相等.
条件:两个角是同一个角的补角;
结论:这两个角相等.
(3) 如果两个角是锐角,那么这两个角互为余角.
条件:两个角是锐角;
结论:这两个角互为余角.
23. ,; 平分
因为 ,
所以 ,.
又因为 ,
所以 ,
即 平分 .(答案不唯一)
24. ,,
,
,
.
,
,
.
25. 猜想:.
证明:如图所示,过点 作 ,
所以 (两直线平行,内错角相等).
因为 ,
所以 ,
所以 .
因为 ,
所以 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
