2021—2022学年北师大版数学九年级下册2.3.2确定二次函数的表达式课件(共18张PPT)
文档属性
| 名称 | 2021—2022学年北师大版数学九年级下册2.3.2确定二次函数的表达式课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 543.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 09:31:43 | ||
图片预览






文档简介
(共18张PPT)
第二章 二次函数
2.3.2.确定二次函数的表达式(二)
温故知新
顶点式
对称轴:
顶点坐标:
x = h
(h,k)
y = a( x - h )2 + k
一般式 y=ax +bx+c
对称轴是:
顶点坐标是:
b
2a
-
,
4ac-b
4a
)
(
b
2a
-
x=
直线
温故知新
确定二次函数表达式的方法:
(1)对于一般式y=ax2+bx+c,
再加_____条件就可以确定表达式;
已知一项的系数,
两个
(2)对于顶点坐标式y=a(x-h)2+k 。
再加_____条件就可以确定表达式。
已知顶点坐标,
一个
对于一般式y=ax2+bx+c,
需要几个条件就可以确定表达式呢?
新知探究
例1.已知二次函数的图像经过(-1, 10),(1, 4)、(2, 7)三点,求这个二次函数的表达式,并写出它的对称轴和顶点坐标。
解:
设二次函数表达式为
解得
将点(-1,10)、(1,4)、(2,7)的坐标分别
y=ax2+bx+c
代入表达式,得
a-b+c =10
a+b+c =4
4a+2b+c =7
a=2
b=-3
c=5
所以,二次函数的表达式为
y=2x2-3x+5
详细解法
新知探究
所以,二次函数的表达式为
y=2x2-3x+5
b
2a
-
4ac-b
4a
化为顶点式:
y=2(x )2
-
3
4
+
31
8
所以,二次函数的对称轴为
顶点坐标为
( , )
31
8
3
4
x=
3
4
=
-3
4
-
3
4
=
8
40
-9
=
31
8
=
利用顶点公式:
归纳
确定二次函数表达式的方法:
(1)对于一般式y=ax2+bx+c,
再加_____条件就可以确定表达式;
已知一项的系数,
两个
(2)对于顶点坐标式y=a(x-h)2+k 。
再加_____条件就可以确定表达式。
已知顶点坐标,
一个
(3)对于一般式y=ax2+bx+c,
需要_____条件就可以确定表达式
三个
议一议
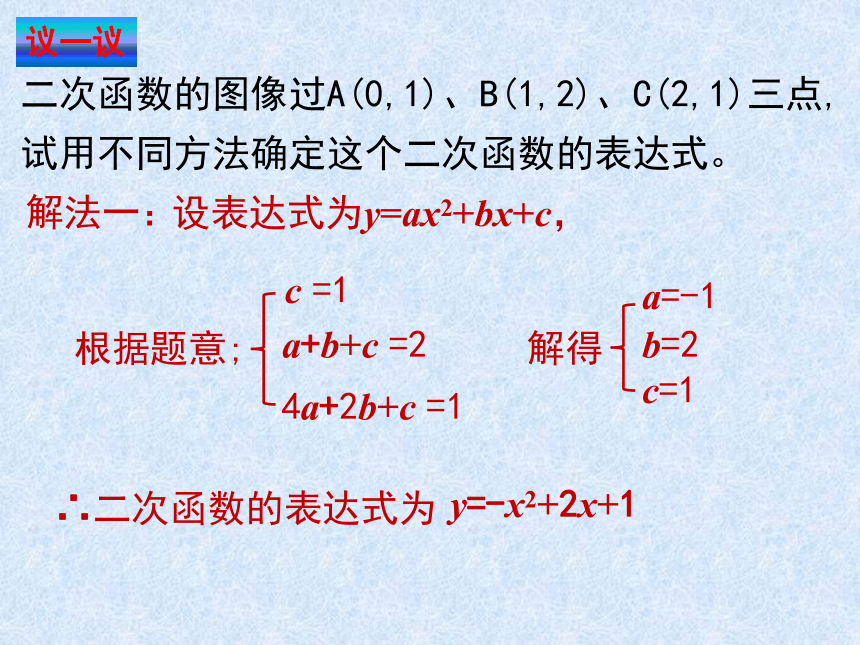
二次函数的图像过A(0,1)、B(1,2)、C(2,1)三点,试用不同方法确定这个二次函数的表达式。
设表达式为y=ax2+bx+c,
解法一:
解得
y=-x2+2x+1
根据题意;
c =1
a+b+c =2
4a+2b+c =1
a=-1
b=2
c=1
∴二次函数的表达式为
议一议
设一般式y=ax2+bx+1,
方法二:
解得:
二次函数的图像过A(0,1)、B(1,2)、C(2,1)三点,试用不同方法确定这个二次函数的表达式。
根据题意;
a+b+1 =2
4a+2b+1 =1
a=-1
b=2
y=-x2+2x+1
∴二次函数的表达式为
新知探究
二次函数的图像过A(0,1)、B(1,2)、C(2,1)三点,试用不同方法确定这个二次函数的表达式。
设一般式y=ax2+bx+1,
方法三:
b
2a
-
=1
a+b+1 =2
解得:
a=-1
b=2
y=-x2+2x+1
∴二次函数的表达式为
x
O
-2 -1 1 2 3
y
3
2
1
-1
-2
归纳
一般式求二次函数的解析式的一般步骤:
4.写出二次函数的解析式。
3.解方程(组);
2.代入已知点的坐标,
得到关于二次函数系数的一次方程(组);
1.设二次函数的表达式:y=ax +bx+c
练一练
1.已知抛物线经过点(-1,0),(3,0),且函数
有最大值5.求抛物线的函数表达式.
根据题意,
表达式可设为:
y = a( x - ___)2 +___
1
5
2.已知二次函数的图象如图所示,则这个二次函数的表达式为( )
A.y=x -2x+3
B.y=x -2x-3
C.y=x +2x-3
D.y=x +2x+3
b
2a
-
x=
a, b异号
B
练一练
练一练
3.已知二次函数的图象如图所示,则这个二次函数的表达式可能是( )
A.y=-x +2x+1
B.y=-x -2x-1
C.y=-x -2x+1
D.y=x +2x+1
x
y
b
2a
-
x=
a, b同号
开口向下
C
练一练
4.根据图中数据求抛物线的函数表达式
设二次函数的表达式为:
y = a( x - 2)2
练一练
4.根据图中数据求抛物线的函数表达式
设二次函数的表达式为:
y=ax +bx
课堂小结
一般式求二次函数的解析式的一般步骤:
4.写出二次函数的解析式。
3.解方程(组);
2.代入已知点的坐标,
得到关于二次函数系数的一次方程(组);
1.设二次函数的表达式:y=ax +bx+c
作业
P45
1,2,
新知探究
a-b+c =10
a+b+c =4
4a+2b+c =7
……①
……②
……③
解方程组的基本思路
②-①得:
2b=-6
∴b=-3
将b=-3分别代入 ②和③得:
a+c =7
4a+c =13
解得:
a=2,
c=5
返回
∴
b=-3
a=2,
c=5
第二章 二次函数
2.3.2.确定二次函数的表达式(二)
温故知新
顶点式
对称轴:
顶点坐标:
x = h
(h,k)
y = a( x - h )2 + k
一般式 y=ax +bx+c
对称轴是:
顶点坐标是:
b
2a
-
,
4ac-b
4a
)
(
b
2a
-
x=
直线
温故知新
确定二次函数表达式的方法:
(1)对于一般式y=ax2+bx+c,
再加_____条件就可以确定表达式;
已知一项的系数,
两个
(2)对于顶点坐标式y=a(x-h)2+k 。
再加_____条件就可以确定表达式。
已知顶点坐标,
一个
对于一般式y=ax2+bx+c,
需要几个条件就可以确定表达式呢?
新知探究
例1.已知二次函数的图像经过(-1, 10),(1, 4)、(2, 7)三点,求这个二次函数的表达式,并写出它的对称轴和顶点坐标。
解:
设二次函数表达式为
解得
将点(-1,10)、(1,4)、(2,7)的坐标分别
y=ax2+bx+c
代入表达式,得
a-b+c =10
a+b+c =4
4a+2b+c =7
a=2
b=-3
c=5
所以,二次函数的表达式为
y=2x2-3x+5
详细解法
新知探究
所以,二次函数的表达式为
y=2x2-3x+5
b
2a
-
4ac-b
4a
化为顶点式:
y=2(x )2
-
3
4
+
31
8
所以,二次函数的对称轴为
顶点坐标为
( , )
31
8
3
4
x=
3
4
=
-3
4
-
3
4
=
8
40
-9
=
31
8
=
利用顶点公式:
归纳
确定二次函数表达式的方法:
(1)对于一般式y=ax2+bx+c,
再加_____条件就可以确定表达式;
已知一项的系数,
两个
(2)对于顶点坐标式y=a(x-h)2+k 。
再加_____条件就可以确定表达式。
已知顶点坐标,
一个
(3)对于一般式y=ax2+bx+c,
需要_____条件就可以确定表达式
三个
议一议
二次函数的图像过A(0,1)、B(1,2)、C(2,1)三点,试用不同方法确定这个二次函数的表达式。
设表达式为y=ax2+bx+c,
解法一:
解得
y=-x2+2x+1
根据题意;
c =1
a+b+c =2
4a+2b+c =1
a=-1
b=2
c=1
∴二次函数的表达式为
议一议
设一般式y=ax2+bx+1,
方法二:
解得:
二次函数的图像过A(0,1)、B(1,2)、C(2,1)三点,试用不同方法确定这个二次函数的表达式。
根据题意;
a+b+1 =2
4a+2b+1 =1
a=-1
b=2
y=-x2+2x+1
∴二次函数的表达式为
新知探究
二次函数的图像过A(0,1)、B(1,2)、C(2,1)三点,试用不同方法确定这个二次函数的表达式。
设一般式y=ax2+bx+1,
方法三:
b
2a
-
=1
a+b+1 =2
解得:
a=-1
b=2
y=-x2+2x+1
∴二次函数的表达式为
x
O
-2 -1 1 2 3
y
3
2
1
-1
-2
归纳
一般式求二次函数的解析式的一般步骤:
4.写出二次函数的解析式。
3.解方程(组);
2.代入已知点的坐标,
得到关于二次函数系数的一次方程(组);
1.设二次函数的表达式:y=ax +bx+c
练一练
1.已知抛物线经过点(-1,0),(3,0),且函数
有最大值5.求抛物线的函数表达式.
根据题意,
表达式可设为:
y = a( x - ___)2 +___
1
5
2.已知二次函数的图象如图所示,则这个二次函数的表达式为( )
A.y=x -2x+3
B.y=x -2x-3
C.y=x +2x-3
D.y=x +2x+3
b
2a
-
x=
a, b异号
B
练一练
练一练
3.已知二次函数的图象如图所示,则这个二次函数的表达式可能是( )
A.y=-x +2x+1
B.y=-x -2x-1
C.y=-x -2x+1
D.y=x +2x+1
x
y
b
2a
-
x=
a, b同号
开口向下
C
练一练
4.根据图中数据求抛物线的函数表达式
设二次函数的表达式为:
y = a( x - 2)2
练一练
4.根据图中数据求抛物线的函数表达式
设二次函数的表达式为:
y=ax +bx
课堂小结
一般式求二次函数的解析式的一般步骤:
4.写出二次函数的解析式。
3.解方程(组);
2.代入已知点的坐标,
得到关于二次函数系数的一次方程(组);
1.设二次函数的表达式:y=ax +bx+c
作业
P45
1,2,
新知探究
a-b+c =10
a+b+c =4
4a+2b+c =7
……①
……②
……③
解方程组的基本思路
②-①得:
2b=-6
∴b=-3
将b=-3分别代入 ②和③得:
a+c =7
4a+c =13
解得:
a=2,
c=5
返回
∴
b=-3
a=2,
c=5
