安徽省亳州市第五完全中学2022届高三上学期期中考试数学(文)试题(Word版含答案解析)
文档属性
| 名称 | 安徽省亳州市第五完全中学2022届高三上学期期中考试数学(文)试题(Word版含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 523.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 14:59:43 | ||
图片预览



文档简介
亳州市第五完全中学2021-2022学年度第一学期高三年级数学期中考试卷
文科数学
考试时间:120分钟 满分:150分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题(共60分)
1.(本题5分)已知集合,,则( )
A. B. C. D.
2.(本题5分)函数的定义域为( )
A. B. C. D.
3.(本题5分)设,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
4.(本题5分)命题“,”的否定是( )
A., B.,
C., D.,
5.(本题5分)已知函数是幂函数,且在上是减函数,
则实数( )
A.2 B. C.4 D.2或
6.(本题5分)下列函数中,既是奇函数又是增函数的为
A. B. C. D.
7.(本题5分)已知,,,则
A. B. C. D.
8.(本题5分)已知函数,则( )
A.-1 B.0
C.1 D.2
9.(本题5分)设是定义域为的偶函数,且在单调递减,则
A.B.
C.D.
10.(本题5分)已知是定义域为的奇函数,若为偶函数,,则( )
A.-2 B.-1 C.0 D.1
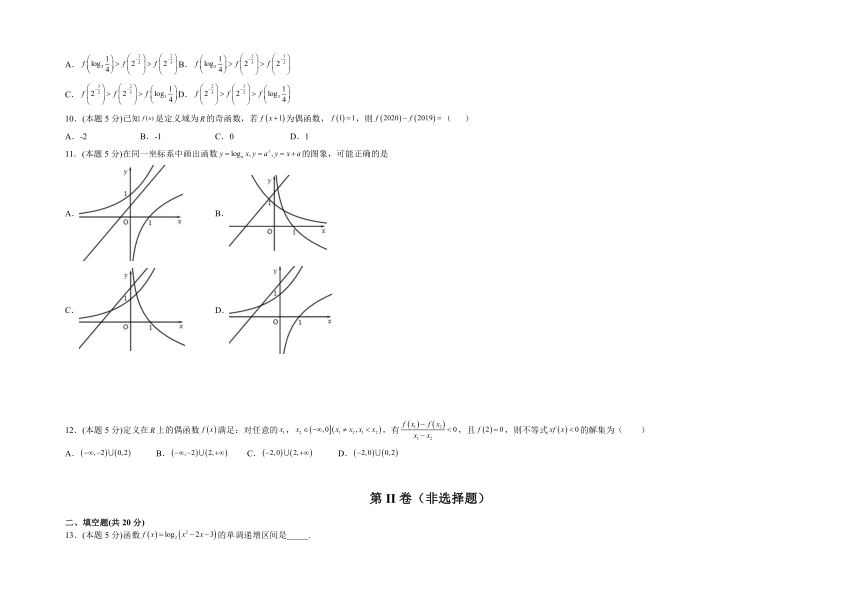
11.(本题5分)在同一坐标系中画出函数的图象,可能正确的是
A. B.
C. D.
12.(本题5分)定义在上的偶函数满足:对任意的,,有,且,则不等式的解集为( )
A. B. C. D.
第II卷(非选择题)
二、填空题(共20分)
13.(本题5分)函数的单调递增区间是_____.
14.(本题5分)已知,且,则__________.
15.(本题5分)已知是奇函数,且时的解析式是,若时,则的表达式为____________.
16.(本题5分)设函数,若,则实数______.
解答题(共70分)
17.(本题10分)已知集合,,.
(1)求; (2)若,求的取值范围.
(本题12分)
已知命题:“,”,命题:“,”,若“且”为真命题,求实数的取值范围.
19.(本题12分)已知是定义在上的奇函数,且当时,.
(1)求函数的解析式;(2)若对任意的,都有不等式恒成立,求实数的取值范围.
20.(本题12分)已知函数.
(1)判断的奇偶性并证明;(2)求证:在上是减函数.
21.(本题12分)已知函数.
(1)若函数在上有最大值,求实数的值;(2)若,解不等式.
22.(本题12分)已知函数的定义域是,且满足,,如果对于,都有.
(1)求的值;(2)解不等式.
参考答案
1.B
解:∵集合,
,∴.故选:B.
2.B
要使函数有意义,则需,解得且,所以.
所以函数的定义域为.故选:B.
3.A
且,∵且,
推不出且,∴“”是“”的充分而不必要条件.
4.B
因为全称命题的否定是特称命题,所以命题“,”的否定是:,.
5.A
解:幂函数中,令,得,解得或;
当时,,函数,在上是减函数,满足题意;
当时,,函数,在上是增函数,不满足题意;
所以实数.
6.D
A是增函数,不是奇函数;B和C都不是定义域内的增函数,排除,只有D正确
7.D
,;.
8.A
解:因为所以,
9.C
是R的偶函数,.
,
又在(0,+∞)单调递减,∴,
,故选C.
10.D
解:根据题意,是定义域为的奇函数,则且,
又由为偶函数,则,则有,
故有,函数是周期为4的周期函数,
故,,
故,
11.D
由于函数互为反函数,所以其图像关于直线y=x对称,由于D选项中a>1,所以直线y=x+a在y轴上的截距也大于1正好相符
12.A
解:∵ 对任意的,,有,
∴ ,∴ 当时,函数为减函数,
又∵ 是偶函数,∴ 当时,为增函数,
∵,∴ ,∴ 当或 时,当时,
又∵ 等价于或
∴不等式的解集为:
13.
依题意,由得:或,即函数的定义域是,
函数在上单调递减,在上单调递增,而在上单调递增,于是得在是单调递减,在上单调递增,
所以函数的单调递增区间为.
14.
由得,,又,所以,则,
所以.故答案为:.
15.
由奇函数的定义知,当时,,那么,故本题正确答案为.
16.
函数当时,,解得,
当时,,解得(舍),实数.
17.(1);(2).
【详解】
(1)因为集合,所以,
(2)由(1)知,①当时,满足,此时,得;②当时,要,则,解得;
由①②得,,综上所述,所求实数的取值范围为.
18.或
【详解】
若是真命题.则对任意恒成立,∴;
若为真命题,则方程有实根,
∴,解得或,
由题意,真也真,∴或.
即实数的取值范围是或.
19.(1);(2).
解:(1)依题可知,解得,所以当时,,
设,则,所以,
又是奇函数,,
即,所以当时,,
综上所述,
(2)当时,,所以在上单调递减,
又是上的奇函数,在上单调递减,
从而在上单调递减,由,
可得,
又在上单调递减,
,即对任意的恒成立,
则,解得或,故的取值范围是.
20.
【详解】
(1)由解得或,所以的定义域为.
为奇函数,证明如下:
,
所以为奇函数.
当时, 任取x1>x2>1,则0由f(x1)-f(x2)=log2 一 log2 = log2( * ) < log2 , 所以f(x1)-f(x2) < 0, 在上是减函数.
21.(1)或;(2).
【详解】
(1)依题意知:,且
或.
(2)若,由
,
故原不等式的解集为.
22.(1) (2).
【详解】
(1)令,则,.
(2)解法一:由,都有知为上的减函数,且,即.
∵,且,
∴可化为,即=,
则,解得.
∴不等式的解集为.
文科数学
考试时间:120分钟 满分:150分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题(共60分)
1.(本题5分)已知集合,,则( )
A. B. C. D.
2.(本题5分)函数的定义域为( )
A. B. C. D.
3.(本题5分)设,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
4.(本题5分)命题“,”的否定是( )
A., B.,
C., D.,
5.(本题5分)已知函数是幂函数,且在上是减函数,
则实数( )
A.2 B. C.4 D.2或
6.(本题5分)下列函数中,既是奇函数又是增函数的为
A. B. C. D.
7.(本题5分)已知,,,则
A. B. C. D.
8.(本题5分)已知函数,则( )
A.-1 B.0
C.1 D.2
9.(本题5分)设是定义域为的偶函数,且在单调递减,则
A.B.
C.D.
10.(本题5分)已知是定义域为的奇函数,若为偶函数,,则( )
A.-2 B.-1 C.0 D.1
11.(本题5分)在同一坐标系中画出函数的图象,可能正确的是
A. B.
C. D.
12.(本题5分)定义在上的偶函数满足:对任意的,,有,且,则不等式的解集为( )
A. B. C. D.
第II卷(非选择题)
二、填空题(共20分)
13.(本题5分)函数的单调递增区间是_____.
14.(本题5分)已知,且,则__________.
15.(本题5分)已知是奇函数,且时的解析式是,若时,则的表达式为____________.
16.(本题5分)设函数,若,则实数______.
解答题(共70分)
17.(本题10分)已知集合,,.
(1)求; (2)若,求的取值范围.
(本题12分)
已知命题:“,”,命题:“,”,若“且”为真命题,求实数的取值范围.
19.(本题12分)已知是定义在上的奇函数,且当时,.
(1)求函数的解析式;(2)若对任意的,都有不等式恒成立,求实数的取值范围.
20.(本题12分)已知函数.
(1)判断的奇偶性并证明;(2)求证:在上是减函数.
21.(本题12分)已知函数.
(1)若函数在上有最大值,求实数的值;(2)若,解不等式.
22.(本题12分)已知函数的定义域是,且满足,,如果对于,都有.
(1)求的值;(2)解不等式.
参考答案
1.B
解:∵集合,
,∴.故选:B.
2.B
要使函数有意义,则需,解得且,所以.
所以函数的定义域为.故选:B.
3.A
且,∵且,
推不出且,∴“”是“”的充分而不必要条件.
4.B
因为全称命题的否定是特称命题,所以命题“,”的否定是:,.
5.A
解:幂函数中,令,得,解得或;
当时,,函数,在上是减函数,满足题意;
当时,,函数,在上是增函数,不满足题意;
所以实数.
6.D
A是增函数,不是奇函数;B和C都不是定义域内的增函数,排除,只有D正确
7.D
,;.
8.A
解:因为所以,
9.C
是R的偶函数,.
,
又在(0,+∞)单调递减,∴,
,故选C.
10.D
解:根据题意,是定义域为的奇函数,则且,
又由为偶函数,则,则有,
故有,函数是周期为4的周期函数,
故,,
故,
11.D
由于函数互为反函数,所以其图像关于直线y=x对称,由于D选项中a>1,所以直线y=x+a在y轴上的截距也大于1正好相符
12.A
解:∵ 对任意的,,有,
∴ ,∴ 当时,函数为减函数,
又∵ 是偶函数,∴ 当时,为增函数,
∵,∴ ,∴ 当或 时,当时,
又∵ 等价于或
∴不等式的解集为:
13.
依题意,由得:或,即函数的定义域是,
函数在上单调递减,在上单调递增,而在上单调递增,于是得在是单调递减,在上单调递增,
所以函数的单调递增区间为.
14.
由得,,又,所以,则,
所以.故答案为:.
15.
由奇函数的定义知,当时,,那么,故本题正确答案为.
16.
函数当时,,解得,
当时,,解得(舍),实数.
17.(1);(2).
【详解】
(1)因为集合,所以,
(2)由(1)知,①当时,满足,此时,得;②当时,要,则,解得;
由①②得,,综上所述,所求实数的取值范围为.
18.或
【详解】
若是真命题.则对任意恒成立,∴;
若为真命题,则方程有实根,
∴,解得或,
由题意,真也真,∴或.
即实数的取值范围是或.
19.(1);(2).
解:(1)依题可知,解得,所以当时,,
设,则,所以,
又是奇函数,,
即,所以当时,,
综上所述,
(2)当时,,所以在上单调递减,
又是上的奇函数,在上单调递减,
从而在上单调递减,由,
可得,
又在上单调递减,
,即对任意的恒成立,
则,解得或,故的取值范围是.
20.
【详解】
(1)由解得或,所以的定义域为.
为奇函数,证明如下:
,
所以为奇函数.
当时, 任取x1>x2>1,则0
21.(1)或;(2).
【详解】
(1)依题意知:,且
或.
(2)若,由
,
故原不等式的解集为.
22.(1) (2).
【详解】
(1)令,则,.
(2)解法一:由,都有知为上的减函数,且,即.
∵,且,
∴可化为,即=,
则,解得.
∴不等式的解集为.
同课章节目录
