安徽省合肥市瑶海区三十中2021-2022学年九年级上学期期末预测绿色数学试卷(word版含答案)
文档属性
| 名称 | 安徽省合肥市瑶海区三十中2021-2022学年九年级上学期期末预测绿色数学试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 421.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 00:49:46 | ||
图片预览

文档简介
合肥瑶海区三十中2021-2022学年九上期末预测绿色数学试卷(含答案)
温馨提示:本试卷内容涵盖沪科版九年级21.1~24.3、共4页八大题、23小题,满分150分,时间120分钟
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列汽车标志中既是轴对称图形又是中心对称图形的是( )
A B C D
2.若一次函数y=ax+b (a≠0)的图象与x轴的交点坐标为(–2,0),则抛物线y=ax+bx的对称轴为( )
A. 直线x=1 B. 直线x=–2 C. 直线x=–1 D. 直线x=–4
3.在Rt△ACB中,∠C=90°,AC=1、BC=2,则sinB的值为( )
A B C D
4.如图,在ΔABC中,D、E分别是边BC、AC上的点,AD与BE相交于点F,若E为AC的中点,BD:DC=2:3,则AF:FD的值是( )
A.2.5 B.3 C. 4 D.2
第4题图 第5题图 第6题图
5.如图,⊙0的弦AB=6,半径OD⊥AB交AB于点D、交弧AB于点C.若CD=1,则⊙0的半径为( )
A. 4 B. 5 C. 6 D. 7
6.如图,点A在反比例函数y=上,点B在x轴上,连接AB交y轴于点E,将AB沿x轴向右平移至CD,其中C在x轴上,D在y轴上,连接CE,若△CDE的面积为3,则k的值为( )
A. – 3 B.3 C. – 6 D.6
7.如图大坝的横断面,斜坡AB的坡比i=1:2,背水坡CD的坡比i=1:1,若坡面CD的长度为6米,则斜坡AB的长度为( )
A. 4 B. 6 C. 6 D. 24
第7题图 第8题图 第9题图
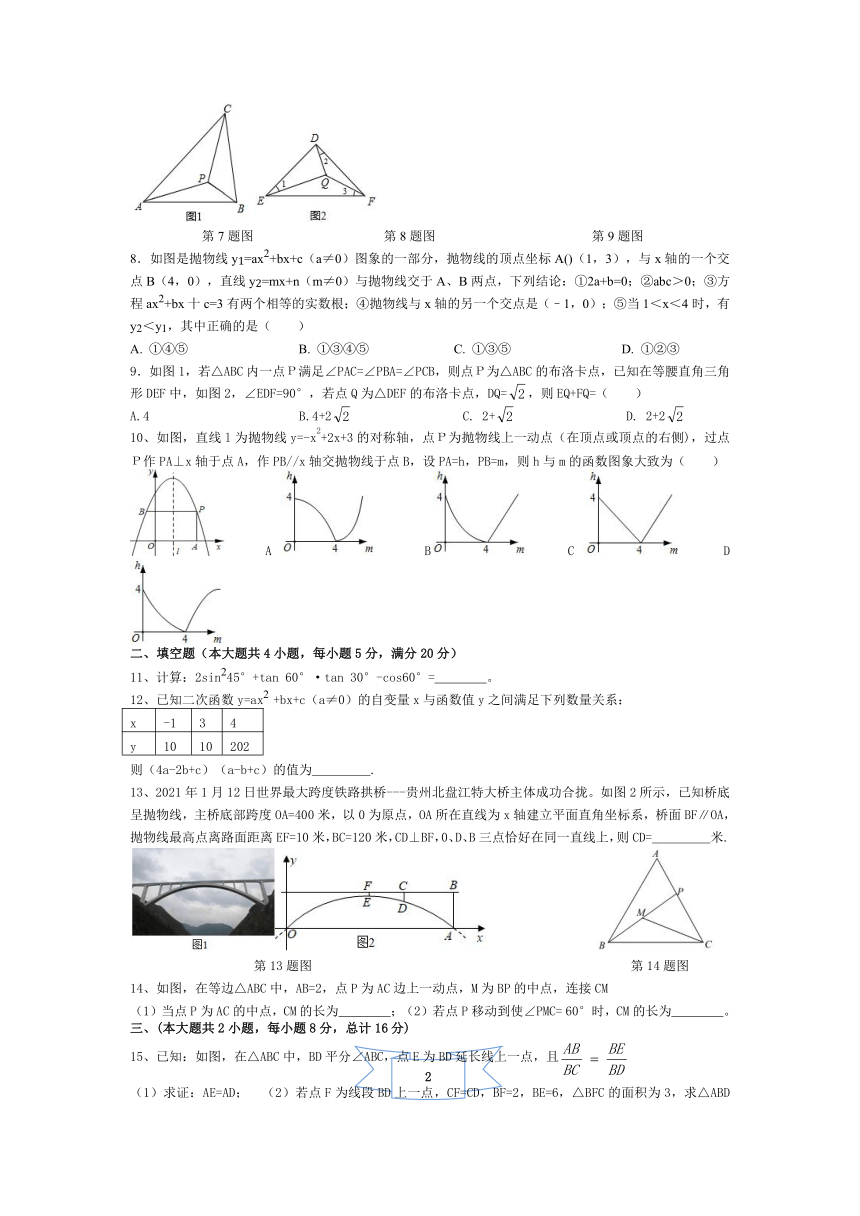
8.如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A()(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A、B两点,下列结论:①2a+b=0;②abc>0;③方程ax2+bx十c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(–1,0);⑤当1<x<4时,有y2<y1,其中正确的是( )
A. ①④⑤ B. ①③④⑤ C. ①③⑤ D. ①②③
9.如图1,若△ABC内一点Р满足∠PAC=∠PBA=∠PCB,则点Р为△ABC的布洛卡点,已知在等腰直角三角形DEF中,如图2,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=,则EQ+FQ=( )
A.4 B.4+2 C. 2+ D. 2+2
10、如图,直线l为抛物线y=-x2+2x+3的对称轴,点Р为抛物线上一动点(在顶点或顶点的右侧),过点Р作PA⊥x轴于点A,作PB//x轴交抛物线于点B,设PA=h,PB=m,则h与m的函数图象大致为( )
A B C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11、计算:2sin45°+tan 60°·tan 30°-cos60°= 。
12、已知二次函数y=ax +bx+c(a≠0)的自变量x与函数值y之间满足下列数量关系:
x -1 3 4
y 10 10 202
则(4a-2b+c)(a-b+c)的值为 .
13、2021年1月12日世界最大跨度铁路拱桥---贵州北盘江特大桥主体成功合拢。如图2所示,已知桥底呈抛物线,主桥底部跨度OA=400米,以0为原点,OA所在直线为x轴建立平面直角坐标系,桥面BF∥OA,抛物线最高点离路面距离EF=10米,BC=120米,CD⊥BF,0、D、B三点恰好在同一直线上,则CD= 米.
第13题图 第14题图
14、如图,在等边△ABC中,AB=2,点P为AC边上一动点,M为BP的中点,连接CM
(1)当点P为AC的中点,CM的长为 ;(2)若点P移动到使∠PMC= 60°时,CM的长为 。
三、(本大题共2小题,每小题8分,总计16分)
15、已知:如图,在△ABC中,BD平分∠ABC,点E为BD延长线上一点,且
(1)求证:AE=AD; (2)若点F为线段BD上一点,CF=CD,BF=2,BE=6,△BFC的面积为3,求△ABD的面积;
16、为了预防新冠病毒的传播,某校对教室采取喷洒药物消毒,在对某教室进行消毒的过程中,先经过5分钟的集中药物喷洒,再封闭教室10分钟,然后打开门窗进行通风,室内每立方米空气中含药量y(mg/m)与药物在空气中的持续时间x(分钟)之间的函数关系,在打开门窗通风前分别满足两一次函数,在通风后又成反比例,如图所示.
(1)问:室内空气中的含药量不低于8mg/m3的持续时间可达到几分钟?
(2)当室内空气中的含药量不低于5mg/m且持续时间不低于30分钟时,才能完全有效杀灭传染病毒,试通过分析判断此次消毒是否完全有效?
四、(本大题共2小题,每小题8分,总计16分)
17、如图所示,巡逻船在A处测得灯塔C在北偏东45°方向上,距离A处30km,在灯塔C的正南方向B处有一渔船发出求救信号,巡逻船接到指示后立即前往施救,已知B处在A处的北偏东60°方向上,这时巡逻船与渔船的距离是多少?(精确到0.01km,参考数据:=1.414,≈1.732,≈2.449)
18、如图,AB是⊙0的直径,点C、D是⊙0上的点,且0D//BC,AC分别与BD、OD相交于点E、F。
(1)求证:点D为AC的中点; (2)若DF=7、AC=24,求00的直径;
五、(本大题共2小题,每小题10分,总计20分)
19、如图,在平面坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,-4)
(1)请在图中,画出将△ABC绕点0逆时针旋转90°得到的△A1B1C1;
(2)以点0为位似中心,将△ABC缩小为原来的,得到△A2B2C2,请在图中y轴右侧,画△A2B2C2;
(3)tan∠BAC= 。
20、已知A(a,-2a)、B(-2,a)两点是反比例函数与一次函数y= kx+b图象的两个交点。
(1)求一次函数和反比例函数的解析式; (2)求△ABO的面积;
(3)观察图象,直接写出不等式kx+b->0的解集.
六、(本大题共1小题,每小题12分,总计12分)
21、已知二次函数y=-x+mx+m(m≠0)的图象与x轴交于A、B两点(A在B点的左侧),与y轴交点C,顶点为D.
(1)若A点在x负半轴上,且0A=OC,求该二次函数解析式;
(2)用含m的代数式表示顶点D的纵坐标,并求纵坐标的最小值;
(3)若-2≤m≤4,且当-1≤x≤2时,y的最大值为3,直接写出m的值 。
七、(本大题共1小题,每小题12分,总计12分)
22、要建如图所示两个长方形养鸡场,为了节约材料,鸡场的一边靠着原有的一条墙长a=20m,另外的边用竹篱笆围成,已知篱笆总长为32m,且在BC边上开一扇长为2m的门GH,在EF边上开一扇长为2m的门MN,若设鸡场的AB长为xm
(1)若两个鸡场的总面积为S,求S关了x的关系式,并求出x的取值范围;
(2)若两个鸡场总面积为96m,求x;
(3)直接写出当鸡场的总面积不小于105m时,x的取值范围是 。
八、(本大题共1小题,每小题14分,总计14分)
23、△ABC中,∠ABC=90°,BD⊥AC,点E为BD的中点,连接AE并延长交BC于点F,且有AF=CF,过F点作
FH⊥AC于点H.
(1)求证:△ADE~△CDB; (2)求证:AE=2EF; (3)若FH=,求BC的长.
合肥瑶海区三十中2021-2022学年九上期末预测绿色数学试卷(含答案)
1 2 3 4 5 6 7 8 9 10
D C B A B C C C C A
11、 12、 2020; 13、 18; 14、 (1) ; (2);
17、24.49km;
20、(1);y=-x-1; (2); (3)x<-2或0<x<1;
21、(1)y-x+x+; (2)yD=m+m;最小值为-1; (3)2;
22、(1)s=-3x+3x(); (2)x=4或8; (3);
温馨提示:本试卷内容涵盖沪科版九年级21.1~24.3、共4页八大题、23小题,满分150分,时间120分钟
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列汽车标志中既是轴对称图形又是中心对称图形的是( )
A B C D
2.若一次函数y=ax+b (a≠0)的图象与x轴的交点坐标为(–2,0),则抛物线y=ax+bx的对称轴为( )
A. 直线x=1 B. 直线x=–2 C. 直线x=–1 D. 直线x=–4
3.在Rt△ACB中,∠C=90°,AC=1、BC=2,则sinB的值为( )
A B C D
4.如图,在ΔABC中,D、E分别是边BC、AC上的点,AD与BE相交于点F,若E为AC的中点,BD:DC=2:3,则AF:FD的值是( )
A.2.5 B.3 C. 4 D.2
第4题图 第5题图 第6题图
5.如图,⊙0的弦AB=6,半径OD⊥AB交AB于点D、交弧AB于点C.若CD=1,则⊙0的半径为( )
A. 4 B. 5 C. 6 D. 7
6.如图,点A在反比例函数y=上,点B在x轴上,连接AB交y轴于点E,将AB沿x轴向右平移至CD,其中C在x轴上,D在y轴上,连接CE,若△CDE的面积为3,则k的值为( )
A. – 3 B.3 C. – 6 D.6
7.如图大坝的横断面,斜坡AB的坡比i=1:2,背水坡CD的坡比i=1:1,若坡面CD的长度为6米,则斜坡AB的长度为( )
A. 4 B. 6 C. 6 D. 24
第7题图 第8题图 第9题图
8.如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A()(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A、B两点,下列结论:①2a+b=0;②abc>0;③方程ax2+bx十c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(–1,0);⑤当1<x<4时,有y2<y1,其中正确的是( )
A. ①④⑤ B. ①③④⑤ C. ①③⑤ D. ①②③
9.如图1,若△ABC内一点Р满足∠PAC=∠PBA=∠PCB,则点Р为△ABC的布洛卡点,已知在等腰直角三角形DEF中,如图2,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=,则EQ+FQ=( )
A.4 B.4+2 C. 2+ D. 2+2
10、如图,直线l为抛物线y=-x2+2x+3的对称轴,点Р为抛物线上一动点(在顶点或顶点的右侧),过点Р作PA⊥x轴于点A,作PB//x轴交抛物线于点B,设PA=h,PB=m,则h与m的函数图象大致为( )
A B C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11、计算:2sin45°+tan 60°·tan 30°-cos60°= 。
12、已知二次函数y=ax +bx+c(a≠0)的自变量x与函数值y之间满足下列数量关系:
x -1 3 4
y 10 10 202
则(4a-2b+c)(a-b+c)的值为 .
13、2021年1月12日世界最大跨度铁路拱桥---贵州北盘江特大桥主体成功合拢。如图2所示,已知桥底呈抛物线,主桥底部跨度OA=400米,以0为原点,OA所在直线为x轴建立平面直角坐标系,桥面BF∥OA,抛物线最高点离路面距离EF=10米,BC=120米,CD⊥BF,0、D、B三点恰好在同一直线上,则CD= 米.
第13题图 第14题图
14、如图,在等边△ABC中,AB=2,点P为AC边上一动点,M为BP的中点,连接CM
(1)当点P为AC的中点,CM的长为 ;(2)若点P移动到使∠PMC= 60°时,CM的长为 。
三、(本大题共2小题,每小题8分,总计16分)
15、已知:如图,在△ABC中,BD平分∠ABC,点E为BD延长线上一点,且
(1)求证:AE=AD; (2)若点F为线段BD上一点,CF=CD,BF=2,BE=6,△BFC的面积为3,求△ABD的面积;
16、为了预防新冠病毒的传播,某校对教室采取喷洒药物消毒,在对某教室进行消毒的过程中,先经过5分钟的集中药物喷洒,再封闭教室10分钟,然后打开门窗进行通风,室内每立方米空气中含药量y(mg/m)与药物在空气中的持续时间x(分钟)之间的函数关系,在打开门窗通风前分别满足两一次函数,在通风后又成反比例,如图所示.
(1)问:室内空气中的含药量不低于8mg/m3的持续时间可达到几分钟?
(2)当室内空气中的含药量不低于5mg/m且持续时间不低于30分钟时,才能完全有效杀灭传染病毒,试通过分析判断此次消毒是否完全有效?
四、(本大题共2小题,每小题8分,总计16分)
17、如图所示,巡逻船在A处测得灯塔C在北偏东45°方向上,距离A处30km,在灯塔C的正南方向B处有一渔船发出求救信号,巡逻船接到指示后立即前往施救,已知B处在A处的北偏东60°方向上,这时巡逻船与渔船的距离是多少?(精确到0.01km,参考数据:=1.414,≈1.732,≈2.449)
18、如图,AB是⊙0的直径,点C、D是⊙0上的点,且0D//BC,AC分别与BD、OD相交于点E、F。
(1)求证:点D为AC的中点; (2)若DF=7、AC=24,求00的直径;
五、(本大题共2小题,每小题10分,总计20分)
19、如图,在平面坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,-4)
(1)请在图中,画出将△ABC绕点0逆时针旋转90°得到的△A1B1C1;
(2)以点0为位似中心,将△ABC缩小为原来的,得到△A2B2C2,请在图中y轴右侧,画△A2B2C2;
(3)tan∠BAC= 。
20、已知A(a,-2a)、B(-2,a)两点是反比例函数与一次函数y= kx+b图象的两个交点。
(1)求一次函数和反比例函数的解析式; (2)求△ABO的面积;
(3)观察图象,直接写出不等式kx+b->0的解集.
六、(本大题共1小题,每小题12分,总计12分)
21、已知二次函数y=-x+mx+m(m≠0)的图象与x轴交于A、B两点(A在B点的左侧),与y轴交点C,顶点为D.
(1)若A点在x负半轴上,且0A=OC,求该二次函数解析式;
(2)用含m的代数式表示顶点D的纵坐标,并求纵坐标的最小值;
(3)若-2≤m≤4,且当-1≤x≤2时,y的最大值为3,直接写出m的值 。
七、(本大题共1小题,每小题12分,总计12分)
22、要建如图所示两个长方形养鸡场,为了节约材料,鸡场的一边靠着原有的一条墙长a=20m,另外的边用竹篱笆围成,已知篱笆总长为32m,且在BC边上开一扇长为2m的门GH,在EF边上开一扇长为2m的门MN,若设鸡场的AB长为xm
(1)若两个鸡场的总面积为S,求S关了x的关系式,并求出x的取值范围;
(2)若两个鸡场总面积为96m,求x;
(3)直接写出当鸡场的总面积不小于105m时,x的取值范围是 。
八、(本大题共1小题,每小题14分,总计14分)
23、△ABC中,∠ABC=90°,BD⊥AC,点E为BD的中点,连接AE并延长交BC于点F,且有AF=CF,过F点作
FH⊥AC于点H.
(1)求证:△ADE~△CDB; (2)求证:AE=2EF; (3)若FH=,求BC的长.
合肥瑶海区三十中2021-2022学年九上期末预测绿色数学试卷(含答案)
1 2 3 4 5 6 7 8 9 10
D C B A B C C C C A
11、 12、 2020; 13、 18; 14、 (1) ; (2);
17、24.49km;
20、(1);y=-x-1; (2); (3)x<-2或0<x<1;
21、(1)y-x+x+; (2)yD=m+m;最小值为-1; (3)2;
22、(1)s=-3x+3x(); (2)x=4或8; (3);
同课章节目录
