河南省淮阳中学2013届高三富洲部10月第八次周考(数学文)有答案
文档属性
| 名称 | 河南省淮阳中学2013届高三富洲部10月第八次周考(数学文)有答案 | 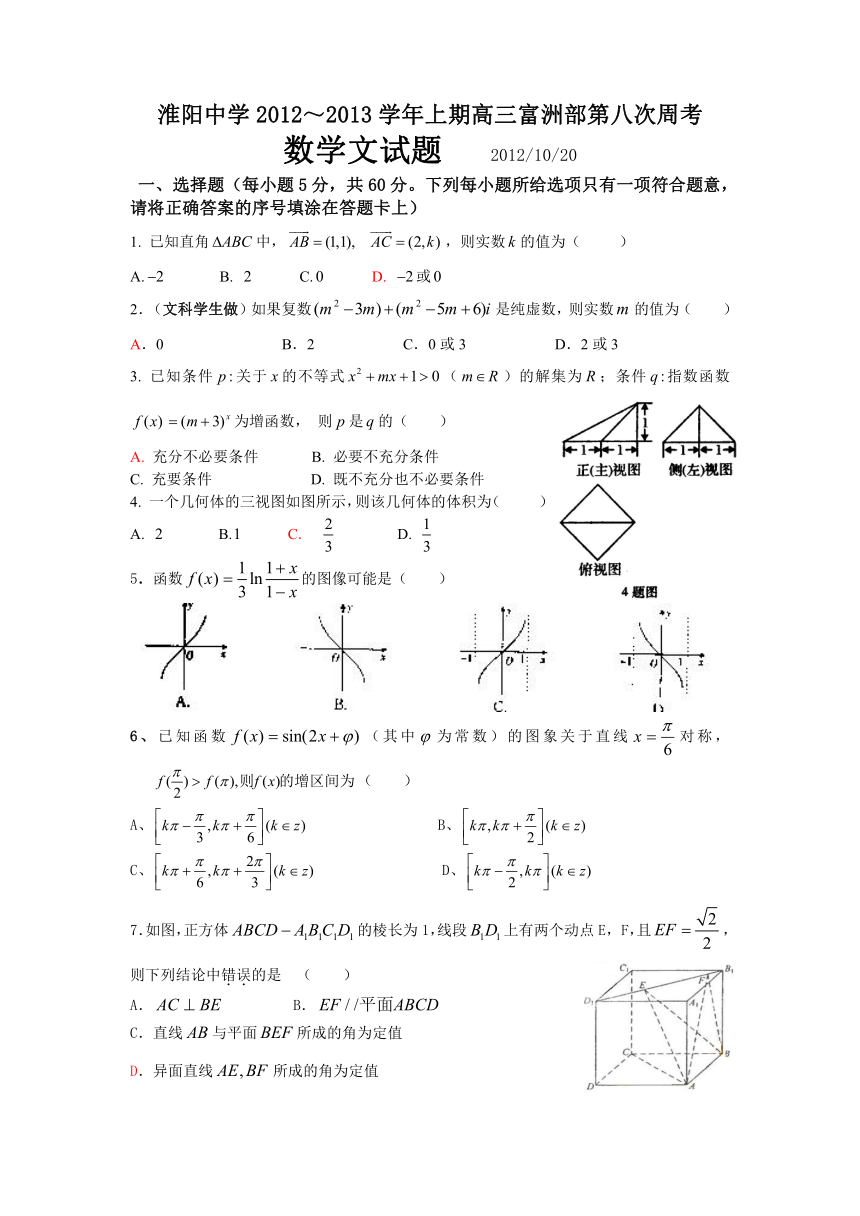 | |
| 格式 | zip | ||
| 文件大小 | 519.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-21 16:24:26 | ||
图片预览





文档简介
淮阳中学2012~2013学年上期高三富洲部第八次周考
数学文试题 2012/10/20
一、选择题(每小题5分,共60分。下列每小题所给选项只有一项符合题意,请将正确答案的序号填涂在答题卡上)
1. 已知直角中,,则实数的值为( )
A. B. C. D. 或
2.(文科学生做)如果复数是纯虚数,则实数的值为( )
A.0 B.2 C.0或3 D.2或3
3. 已知条件关于的不等式()的解集为;条件指数函数为增函数, 则是的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4. 一个几何体的三视图如图所示,则该几何体的体积为( )
A. B. C. D.
5.函数的图像可能是( )
6、已知函数(其中为常数)的图象关于直线对称,( )
A、 B、
C、 D、
7.如图,正方体的棱长为1,线段上有两个动点E, F,且,则下列结论中错误的是 ( )
A. B.
C.直线与平面所成的角为定值
D.异面直线所成的角为定值
8.在△ABC中,角A,B,C所对的边长分别为a,b,c,若∠C=120°,c=a,则( )
A. B.
C. D.a与b的大小关系不能确定
9. (文做)已知函数,则函数的图像的交点的个数为 ( )
A.1 B.2 C.3 D.4
10. 如右图,正三角形所在平面与正方形所在的平面互相垂直,为正方形的中心,为正方形内一点,且满足,则点的轨迹为( )
11.(文科学生做)若函数有最小值,则实数的取值范围是( )
A. B. C. D.
12.在中,D是BC边上任意一点(D与B,C不重合),且,则一定是 ( )
A.直角三角形 B.等边三角形 C.等腰三角形 D.等腰直角三角形
二、填空题(本大题共4个小题,每小题5分,共20分)
13.设则的值等于__
14.设O是△ABC内部一点,且的面积之比为 .
15.△ABC的周长是20,面积是10,A=60°,则BC边的长等于________.
16. 已知球是棱长为12的正四面体的外接球,分别是棱的中点,则平面截球所得截面的面积是 。
三、解答题(本大题共6个小题,共70分. 各题解答必须答在答题卡上规定的矩形区域内。解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)
在中,内角分别对应的边是,已知,.
(Ⅰ)若的面积等于,求;
(Ⅱ)若,求的面积.
18.(本小题满分12分)
在直三棱柱中,
∠ACB=90°,M是 的中点,N是的中点
(1)求证:MN∥平面 ;
(2)求点到平面BMC的距离;
19. (本小题满分12分)
已知角A、B、C是的三个内角,若向量,,且。
(1)求的值; (2)求的最大值。
20.(本小题满分12分)
已知向量=(cosx,sinx),=(cos,-sin),其中x∈[0,]
(1)求·及|+|;
(2)若f(x)=·-2λ|+|的最小值为-,求λ的值
21. (本小题满分12分)
(文科学生做)已知函数().
(1)求函数的单调区间;
(2)函数的图像在处的切线的斜率为若函数,在区间(1,3)上不是单调函数,求 的取值范围。
22. (文科学生做)已知函数.
(Ⅰ)若,求曲线在处切线的斜率;
(Ⅱ)求的单调区间;
(Ⅲ)设,若对任意,均存在,使得,求的取值范围.
淮阳中学2012~2013学年上期高三富洲部第八次周考
数学试题参考答案
一、选择题
1. D. 2.文A 3. A. 4. C 5.C 6. 7.D 8. 9.文D 10. A 11.文C12.C
二、填空题
13. 14.1 15. 7 16.
三、解答题(本大题共6个小题,共75分. 各题解答必须答在答题卡上规定的矩形区域内。解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)
在中,内角分别对应的边是,已知,.
(Ⅰ)若的面积等于,求;
(Ⅱ)若,求的面积.
17. 解:(Ⅰ)由余弦定理及已知条件得,,
又因为的面积等于,所以,得. 2分
联立方程组解得,. 5分
所以的面积. 10分
18.(本小题满分12分)
在直三棱柱中,
∠ACB=90°,M是 的中点,N是的中点
(1)求证:MN∥平面 ;
(2)求点到平面BMC的距离;
(3)(只有理科学生做)求二面角的平面角的余弦值大小。
18:(1)如图所示,取B1C1中点D,连结ND、A1D
∴DN∥BB1∥AA1
又DN=
∴四边形A1MND为平行四边形。
∴MN∥A1 D 又 MN 平面A1B1C1 AD1平面A1B1C1
∴MN∥平面--------------------------4分
(2)因三棱柱为直三棱柱, ∴C1 C ⊥BC,又∠ACB=90°∴BC⊥平面A1MC1
在平面ACC1 A1中,过C1作C1H⊥CM,又BC⊥C1H,故C1H为C1点到平面BMC的距离。
在等腰三角形CMC1中,C1 C=2,CM=C1M=
∴.--------------------------8分
(3)在平面ACC1A1上作CE⊥C1M交C1M于点E,A1C1于点F,
则CE为BE在平面ACC1A1上的射影,
∴BE⊥C1M, ∴∠BEF为二面角B-C1M-A的平面角,
在等腰三角形CMC1中,CE=C1H=,∴tan∠BEC=
∴cos∠BEC=
即二面角的余弦值为。-----------------------12分
19. (本小题满分12分)
已知角A、B、C是的三个内角,若向量,,且。
(1)求的值; (2)求的最大值。
19.解:(1)
(2)
(A,B均是锐角,即其正切均为正)
所求最大值为。
20.(本小题满分12分)
已知向量=(cosx,sinx),=(cos,-sin),其中x∈[0,]
(1)求·及|+|;
(2)若f(x)=·-2λ|+|的最小值为-,求λ的值
20、(1)·=cosxcos-sinxsin=cos2x,|+|==2cosx
(2)f(x)=·-2λ|+|=cos2x-4λcosx=2cos2x-1-4λcosx=2(cosx-λ)2-2λ2-1
∵x∈[0,],故cosx∈[0,1],
若λ<0,当cosx=0时f(x)取最小值-1,不合条件,舍去.
若0≤λ≤1,当cosx=λ时,f(x)取最小值-2λ2-1,令-2λ2-1=-且0≤λ≤1,解得λ=,
若λ>1,当cosx=1时,f(x)取最小值1-4λ, 令1-4λ=-且λ>1,无解
综上:λ=为所求.
21. (本小题满分12分)
(理科学生做)已知函数.
(Ⅰ)若函数在上是增函数,求正实数的取值范围;
(Ⅱ)当时,对任意的正整数,
求证:,且不等式都成立.
21(理科学生做)解:(I)由题设可得
函数在上是增函数,
当时,不等式即恒成立.
当时,的最大值为1,则实数的取值范围是;-----------6分
(Ⅱ)当时,由(Ⅰ)知在上是增函数
对于任意的正整数,有,则--------------8分
(文科学生做)已知函数().
(1)求函数的单调区间;
(2)函数的图像在处的切线的斜率为若函数,在区间(1,3)上不是单调函数,求 的取值范围。
21(文科学生做)解:(I) ……2分
当 即
f(x)的单调递增区间为(0,),单调递减区间为(, ………4分
当 , 即
f(x)的单调递增区间为(,,单调递减区间为(0,) ……6分
(II)得 ……7分
+3 ……8分
………9分
……10分
……12分 即: ……12分
22. (理科学生做)已知函数其中a<0,且a≠-1.
(Ⅰ)讨论函数的单调性;
(Ⅱ)设函数(e是自然对数的底数),是否存在a,使在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由.
22
(文科学生做)已知函数.
(Ⅰ)若,求曲线在处切线的斜率;
(Ⅱ)求的单调区间;
(Ⅲ)设,若对任意,均存在,使得,求的取值范围.
22(文科学生做)解:(1)由已知, ……2分
.
故曲线在处切线的斜率为. ……………4分
(2). ………………5分
①当时,由于,故,
所以,的单调递增区间为. ………………6分
②当时,由,得.
在区间上,,在区间上,
所以,函数的单调递增区间为,单调递减区间为.………7分
(3)由已知,转化为. ………………8分
……………9分
由(Ⅱ)知,当时,在上单调递增,值域为,故不符合题意.
(或者举出反例:存在,故不符合题意.) ……………10分
当时,在上单调递增,在上单调递减,
故的极大值即为最大值,,………11分
所以,
解得. ………………12分
数学文试题 2012/10/20
一、选择题(每小题5分,共60分。下列每小题所给选项只有一项符合题意,请将正确答案的序号填涂在答题卡上)
1. 已知直角中,,则实数的值为( )
A. B. C. D. 或
2.(文科学生做)如果复数是纯虚数,则实数的值为( )
A.0 B.2 C.0或3 D.2或3
3. 已知条件关于的不等式()的解集为;条件指数函数为增函数, 则是的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4. 一个几何体的三视图如图所示,则该几何体的体积为( )
A. B. C. D.
5.函数的图像可能是( )
6、已知函数(其中为常数)的图象关于直线对称,( )
A、 B、
C、 D、
7.如图,正方体的棱长为1,线段上有两个动点E, F,且,则下列结论中错误的是 ( )
A. B.
C.直线与平面所成的角为定值
D.异面直线所成的角为定值
8.在△ABC中,角A,B,C所对的边长分别为a,b,c,若∠C=120°,c=a,则( )
A. B.
C. D.a与b的大小关系不能确定
9. (文做)已知函数,则函数的图像的交点的个数为 ( )
A.1 B.2 C.3 D.4
10. 如右图,正三角形所在平面与正方形所在的平面互相垂直,为正方形的中心,为正方形内一点,且满足,则点的轨迹为( )
11.(文科学生做)若函数有最小值,则实数的取值范围是( )
A. B. C. D.
12.在中,D是BC边上任意一点(D与B,C不重合),且,则一定是 ( )
A.直角三角形 B.等边三角形 C.等腰三角形 D.等腰直角三角形
二、填空题(本大题共4个小题,每小题5分,共20分)
13.设则的值等于__
14.设O是△ABC内部一点,且的面积之比为 .
15.△ABC的周长是20,面积是10,A=60°,则BC边的长等于________.
16. 已知球是棱长为12的正四面体的外接球,分别是棱的中点,则平面截球所得截面的面积是 。
三、解答题(本大题共6个小题,共70分. 各题解答必须答在答题卡上规定的矩形区域内。解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)
在中,内角分别对应的边是,已知,.
(Ⅰ)若的面积等于,求;
(Ⅱ)若,求的面积.
18.(本小题满分12分)
在直三棱柱中,
∠ACB=90°,M是 的中点,N是的中点
(1)求证:MN∥平面 ;
(2)求点到平面BMC的距离;
19. (本小题满分12分)
已知角A、B、C是的三个内角,若向量,,且。
(1)求的值; (2)求的最大值。
20.(本小题满分12分)
已知向量=(cosx,sinx),=(cos,-sin),其中x∈[0,]
(1)求·及|+|;
(2)若f(x)=·-2λ|+|的最小值为-,求λ的值
21. (本小题满分12分)
(文科学生做)已知函数().
(1)求函数的单调区间;
(2)函数的图像在处的切线的斜率为若函数,在区间(1,3)上不是单调函数,求 的取值范围。
22. (文科学生做)已知函数.
(Ⅰ)若,求曲线在处切线的斜率;
(Ⅱ)求的单调区间;
(Ⅲ)设,若对任意,均存在,使得,求的取值范围.
淮阳中学2012~2013学年上期高三富洲部第八次周考
数学试题参考答案
一、选择题
1. D. 2.文A 3. A. 4. C 5.C 6. 7.D 8. 9.文D 10. A 11.文C12.C
二、填空题
13. 14.1 15. 7 16.
三、解答题(本大题共6个小题,共75分. 各题解答必须答在答题卡上规定的矩形区域内。解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)
在中,内角分别对应的边是,已知,.
(Ⅰ)若的面积等于,求;
(Ⅱ)若,求的面积.
17. 解:(Ⅰ)由余弦定理及已知条件得,,
又因为的面积等于,所以,得. 2分
联立方程组解得,. 5分
所以的面积. 10分
18.(本小题满分12分)
在直三棱柱中,
∠ACB=90°,M是 的中点,N是的中点
(1)求证:MN∥平面 ;
(2)求点到平面BMC的距离;
(3)(只有理科学生做)求二面角的平面角的余弦值大小。
18:(1)如图所示,取B1C1中点D,连结ND、A1D
∴DN∥BB1∥AA1
又DN=
∴四边形A1MND为平行四边形。
∴MN∥A1 D 又 MN 平面A1B1C1 AD1平面A1B1C1
∴MN∥平面--------------------------4分
(2)因三棱柱为直三棱柱, ∴C1 C ⊥BC,又∠ACB=90°∴BC⊥平面A1MC1
在平面ACC1 A1中,过C1作C1H⊥CM,又BC⊥C1H,故C1H为C1点到平面BMC的距离。
在等腰三角形CMC1中,C1 C=2,CM=C1M=
∴.--------------------------8分
(3)在平面ACC1A1上作CE⊥C1M交C1M于点E,A1C1于点F,
则CE为BE在平面ACC1A1上的射影,
∴BE⊥C1M, ∴∠BEF为二面角B-C1M-A的平面角,
在等腰三角形CMC1中,CE=C1H=,∴tan∠BEC=
∴cos∠BEC=
即二面角的余弦值为。-----------------------12分
19. (本小题满分12分)
已知角A、B、C是的三个内角,若向量,,且。
(1)求的值; (2)求的最大值。
19.解:(1)
(2)
(A,B均是锐角,即其正切均为正)
所求最大值为。
20.(本小题满分12分)
已知向量=(cosx,sinx),=(cos,-sin),其中x∈[0,]
(1)求·及|+|;
(2)若f(x)=·-2λ|+|的最小值为-,求λ的值
20、(1)·=cosxcos-sinxsin=cos2x,|+|==2cosx
(2)f(x)=·-2λ|+|=cos2x-4λcosx=2cos2x-1-4λcosx=2(cosx-λ)2-2λ2-1
∵x∈[0,],故cosx∈[0,1],
若λ<0,当cosx=0时f(x)取最小值-1,不合条件,舍去.
若0≤λ≤1,当cosx=λ时,f(x)取最小值-2λ2-1,令-2λ2-1=-且0≤λ≤1,解得λ=,
若λ>1,当cosx=1时,f(x)取最小值1-4λ, 令1-4λ=-且λ>1,无解
综上:λ=为所求.
21. (本小题满分12分)
(理科学生做)已知函数.
(Ⅰ)若函数在上是增函数,求正实数的取值范围;
(Ⅱ)当时,对任意的正整数,
求证:,且不等式都成立.
21(理科学生做)解:(I)由题设可得
函数在上是增函数,
当时,不等式即恒成立.
当时,的最大值为1,则实数的取值范围是;-----------6分
(Ⅱ)当时,由(Ⅰ)知在上是增函数
对于任意的正整数,有,则--------------8分
(文科学生做)已知函数().
(1)求函数的单调区间;
(2)函数的图像在处的切线的斜率为若函数,在区间(1,3)上不是单调函数,求 的取值范围。
21(文科学生做)解:(I) ……2分
当 即
f(x)的单调递增区间为(0,),单调递减区间为(, ………4分
当 , 即
f(x)的单调递增区间为(,,单调递减区间为(0,) ……6分
(II)得 ……7分
+3 ……8分
………9分
……10分
……12分 即: ……12分
22. (理科学生做)已知函数其中a<0,且a≠-1.
(Ⅰ)讨论函数的单调性;
(Ⅱ)设函数(e是自然对数的底数),是否存在a,使在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由.
22
(文科学生做)已知函数.
(Ⅰ)若,求曲线在处切线的斜率;
(Ⅱ)求的单调区间;
(Ⅲ)设,若对任意,均存在,使得,求的取值范围.
22(文科学生做)解:(1)由已知, ……2分
.
故曲线在处切线的斜率为. ……………4分
(2). ………………5分
①当时,由于,故,
所以,的单调递增区间为. ………………6分
②当时,由,得.
在区间上,,在区间上,
所以,函数的单调递增区间为,单调递减区间为.………7分
(3)由已知,转化为. ………………8分
……………9分
由(Ⅱ)知,当时,在上单调递增,值域为,故不符合题意.
(或者举出反例:存在,故不符合题意.) ……………10分
当时,在上单调递增,在上单调递减,
故的极大值即为最大值,,………11分
所以,
解得. ………………12分
同课章节目录
