2021-2022学年苏科版七年级数学上册6.3.1 余角、补角、对顶角 课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学上册6.3.1 余角、补角、对顶角 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 598.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 07:35:22 | ||
图片预览




文档简介
(共20张PPT)
6.3.1 余角、补角、对顶角
1
导
入
1平角=
1直角=
∠1+∠2= ∠
AOB
∠ 2=
∠ AOB- ∠1
(1)
B
A
O
2
1
(2)
今天我们继续研究两角之间的关系
2
导
入
85°
15°
3
导
入
85°
15°
4
讲
解
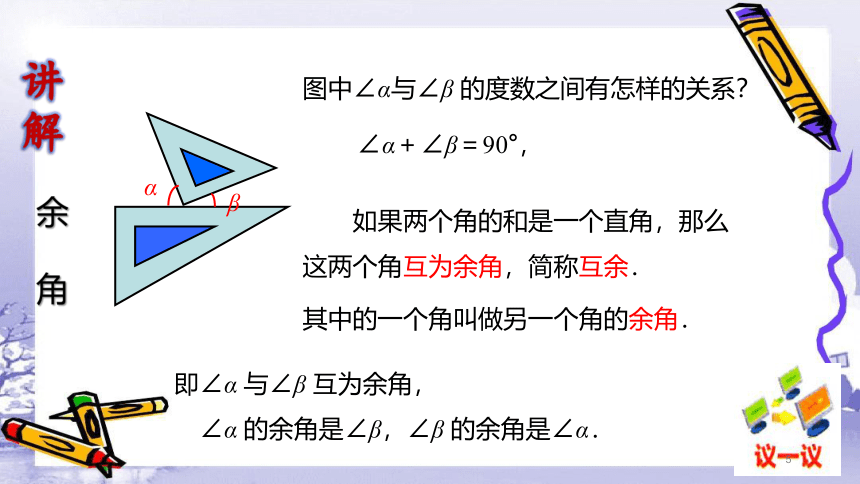
图中∠α与∠β 的度数之间有怎样的关系?
α
β
如果两个角的和是一个直角,那么这两个角互为余角,简称互余.
其中的一个角叫做另一个角的余角.
即∠α 与∠β 互为余角,
∠α 的余角是∠β,∠β 的余角是∠α.
∠α+∠β=90°,
余
角
5
讲
解
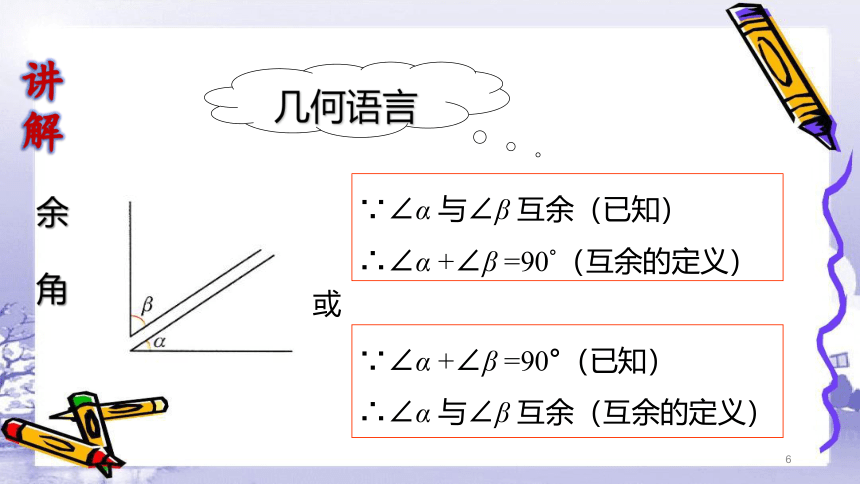
几何语言
∵∠α 与∠β 互余(已知)
∴∠α +∠β =90°(互余的定义)
∵∠α +∠β =90°(已知)
∴∠α 与∠β 互余(互余的定义)
或
余
角
6
讲
解
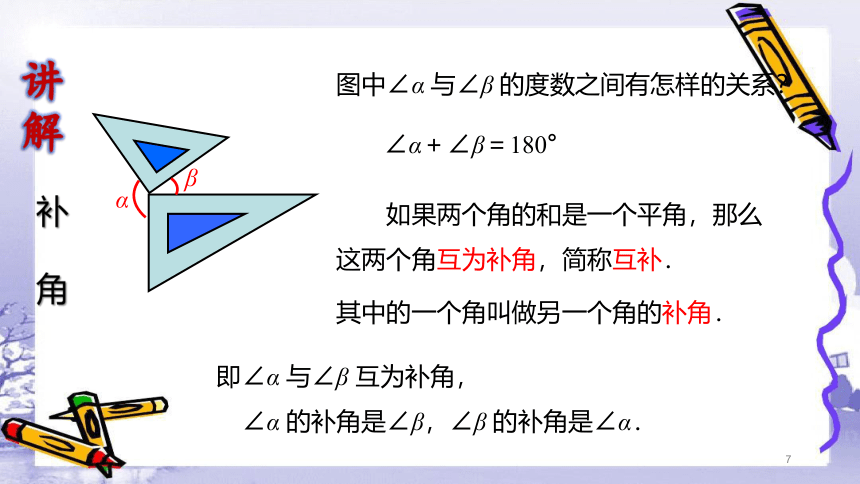
图中∠α 与∠β 的度数之间有怎样的关系?
α
β
如果两个角的和是一个平角,那么
这两个角互为补角,简称互补.
其中的一个角叫做另一个角的补角.
即∠α 与∠β 互为补角,
∠α 的补角是∠β,∠β 的补角是∠α.
∠α+∠β=180°
补
角
7
讲
解
几何语言
∵∠α 与∠β 互补(已知)
∴∠α +∠β =180°(互补的定义)
∵∠α+∠β =180°(已知)
∴∠α 与∠β 互补(互补的定义)
或
补
角
8
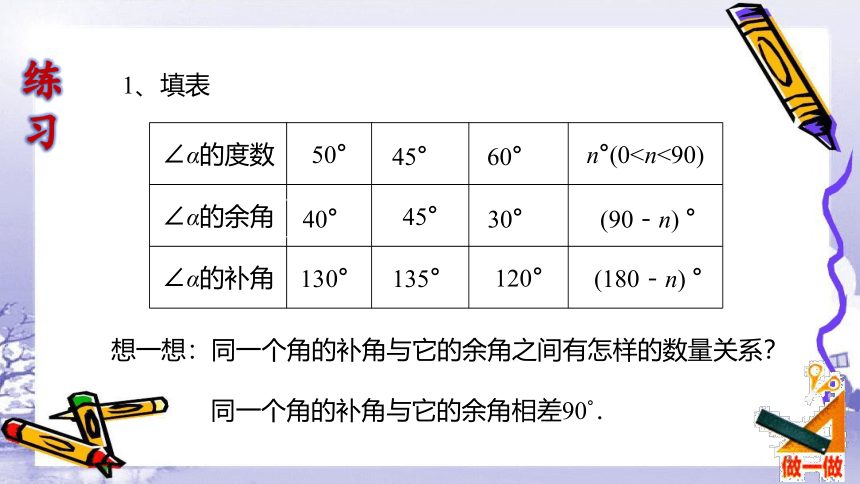
∠α的度数 50° n°(0∠α的余角 45°
∠α的补角 120°
练
习
想一想:同一个角的补角与它的余角之间有怎样的数量关系?
40°
130°
45°
135°
60°
30°
(90-n) °
(180-n) °
同一个角的补角与它的余角相差90°.
1、填表
9
2. 图中给出的各角,哪些互为余角?
10°
44°
25°
65°
46°
80°
55°
2. 图中给出的各角,哪些互为补角?
10°
30°
60°
110°
150°
170°
120°
【收获】:
互余和互补是两个角的数量关系,
与它们的位置无关.
练
习
练
习
10°
55°
75°
145°
100°
35°
80°
105°
125°
170°
10°
15°
35°
55°
115°
3、(1)对A组中的每一个角,在B组中找出它的补角,并用线连接.
(2)B组中有哪些角的余角在C组中?分别找出这些角,并用线连接.
A组
B组
C组
11
讲
解
1
2
3
1. 如图,如果∠1 与∠2 互余,∠1 与∠3 互余,那么∠2 与∠3 相等吗?为什么?
解: ∠2与∠3相等.
因为∠1与∠ 2互为余角, ∠1与∠3互为余角,
所以 ∠ 2= 90 °-∠1, ∠3= 90 °-∠1,
所以∠2=∠3.
同角(或等角)的余角相等
12
讲
解
2.如图,如果∠α 与∠β 互补,∠ α 与∠γ 互补,那么∠ β 与∠ γ 相等吗?为什么?
解: ∠β 与∠γ 相等.
因为∠α 与∠ β 互为补角, ∠α 与∠γ 互为补角,
所以 ∠β= 180 °-∠α ,∠γ= 180 °-∠α
所以∠β =∠γ.
γ
β
α
同角(或等角)的补角相等
13
练
习
A
C
D
B
1、如图,∠A+∠B=90°,∠BCD+∠B=90°,
则∠A与∠BCD有怎样的大小关系?为什么?
∵ ∠A+∠B=90°
∴ ∠A与∠B互余
解:∠A=∠BCD
∴ ∠A=∠BCD
(同角的余角相等)
∵ ∠BCD+∠B=90°
∴ ∠BCD与∠B互余
14
练
习
2、已知∠α 与∠β 互为补角,且∠β 比∠α 大30°,求∠α、∠β的度数 .
解:根据题意,可得∠β=∠α+30°,
因为∠α 与∠β 互为补角,
所以∠α+∠β=180°,
即∠α+(∠α+30°)=180°,
所以∠α=75°,
∠β=75°+30°=105°.
15
练
习
解:
∠α 的余角 = 90°-∠α = 90°-27° = 63°
∠α 的补角 = 180°-∠α = 180°-27° = 153°
3、已知 ∠α=27°,求∠α 的余角和补角的度数.
∠α 的余角的补角是___________
∠α 的补角是____________
∠α 的余角是__________
29°26′
119°26′
150°34′
4、已知∠α = 60°34′,求∠α 的余角、补角和余角的补角.
16
练
习
5、已知一个角的补角是这个角的余角的4倍,求这个角
的度数.
解:设这个角为x度,
则这个角的余角是(90-x)°,
补角是(180-x) °
由题意得,
180-x = 4(90-x)
解得:x = 60
这个角的度数为60°.
17
18
6.已知∠A的余角是它的2倍,求∠A的度数。
7.已知∠B是它补角的3倍,求∠B的度数。
6.解:设∠A为x°,则它的余角为(2x)°,得
X+2x=90,x=30°
答:∠A是30°。
7.解:设∠B为x°则它的补角为(180-x)°得
X=3(180-x), x=135
答:∠B是135°。
练
习
19
8 如图,O是直线AB上的一点,OC平分∠AOB,∠DOE=90o,则
(1)∠2=∠( ),∠1=∠( )
(2)图中,互为余角的角共有哪几对?
( )
(3)图中,∠DOB的补角是 。
4
3
∠1与∠2,∠1与∠4,∠2与∠3,∠4与∠3
∠1,∠3
A
1
4
3
2
B
C
D
E
O
F
(4)延长EO到F,∠COF与∠ BOD的大小关系怎样?
解: ∠COF=∠ BOD
理由:∵ ∠COF+∠ 3=1800
∠ BOD+∠1=1800
又∵∠ 1 = ∠3
∴ ∠COF=∠ BOD
练
习
总
结
(1)余角、补角的概念
注意:余角、补角与两个角的大小有关系,与它们的位置没有关系.
(2)余角、补角的性质
同角(或等角)的余角相等
同角(或等角)的补角相等
20
6.3.1 余角、补角、对顶角
1
导
入
1平角=
1直角=
∠1+∠2= ∠
AOB
∠ 2=
∠ AOB- ∠1
(1)
B
A
O
2
1
(2)
今天我们继续研究两角之间的关系
2
导
入
85°
15°
3
导
入
85°
15°
4
讲
解
图中∠α与∠β 的度数之间有怎样的关系?
α
β
如果两个角的和是一个直角,那么这两个角互为余角,简称互余.
其中的一个角叫做另一个角的余角.
即∠α 与∠β 互为余角,
∠α 的余角是∠β,∠β 的余角是∠α.
∠α+∠β=90°,
余
角
5
讲
解
几何语言
∵∠α 与∠β 互余(已知)
∴∠α +∠β =90°(互余的定义)
∵∠α +∠β =90°(已知)
∴∠α 与∠β 互余(互余的定义)
或
余
角
6
讲
解
图中∠α 与∠β 的度数之间有怎样的关系?
α
β
如果两个角的和是一个平角,那么
这两个角互为补角,简称互补.
其中的一个角叫做另一个角的补角.
即∠α 与∠β 互为补角,
∠α 的补角是∠β,∠β 的补角是∠α.
∠α+∠β=180°
补
角
7
讲
解
几何语言
∵∠α 与∠β 互补(已知)
∴∠α +∠β =180°(互补的定义)
∵∠α+∠β =180°(已知)
∴∠α 与∠β 互补(互补的定义)
或
补
角
8
∠α的度数 50° n°(0
∠α的补角 120°
练
习
想一想:同一个角的补角与它的余角之间有怎样的数量关系?
40°
130°
45°
135°
60°
30°
(90-n) °
(180-n) °
同一个角的补角与它的余角相差90°.
1、填表
9
2. 图中给出的各角,哪些互为余角?
10°
44°
25°
65°
46°
80°
55°
2. 图中给出的各角,哪些互为补角?
10°
30°
60°
110°
150°
170°
120°
【收获】:
互余和互补是两个角的数量关系,
与它们的位置无关.
练
习
练
习
10°
55°
75°
145°
100°
35°
80°
105°
125°
170°
10°
15°
35°
55°
115°
3、(1)对A组中的每一个角,在B组中找出它的补角,并用线连接.
(2)B组中有哪些角的余角在C组中?分别找出这些角,并用线连接.
A组
B组
C组
11
讲
解
1
2
3
1. 如图,如果∠1 与∠2 互余,∠1 与∠3 互余,那么∠2 与∠3 相等吗?为什么?
解: ∠2与∠3相等.
因为∠1与∠ 2互为余角, ∠1与∠3互为余角,
所以 ∠ 2= 90 °-∠1, ∠3= 90 °-∠1,
所以∠2=∠3.
同角(或等角)的余角相等
12
讲
解
2.如图,如果∠α 与∠β 互补,∠ α 与∠γ 互补,那么∠ β 与∠ γ 相等吗?为什么?
解: ∠β 与∠γ 相等.
因为∠α 与∠ β 互为补角, ∠α 与∠γ 互为补角,
所以 ∠β= 180 °-∠α ,∠γ= 180 °-∠α
所以∠β =∠γ.
γ
β
α
同角(或等角)的补角相等
13
练
习
A
C
D
B
1、如图,∠A+∠B=90°,∠BCD+∠B=90°,
则∠A与∠BCD有怎样的大小关系?为什么?
∵ ∠A+∠B=90°
∴ ∠A与∠B互余
解:∠A=∠BCD
∴ ∠A=∠BCD
(同角的余角相等)
∵ ∠BCD+∠B=90°
∴ ∠BCD与∠B互余
14
练
习
2、已知∠α 与∠β 互为补角,且∠β 比∠α 大30°,求∠α、∠β的度数 .
解:根据题意,可得∠β=∠α+30°,
因为∠α 与∠β 互为补角,
所以∠α+∠β=180°,
即∠α+(∠α+30°)=180°,
所以∠α=75°,
∠β=75°+30°=105°.
15
练
习
解:
∠α 的余角 = 90°-∠α = 90°-27° = 63°
∠α 的补角 = 180°-∠α = 180°-27° = 153°
3、已知 ∠α=27°,求∠α 的余角和补角的度数.
∠α 的余角的补角是___________
∠α 的补角是____________
∠α 的余角是__________
29°26′
119°26′
150°34′
4、已知∠α = 60°34′,求∠α 的余角、补角和余角的补角.
16
练
习
5、已知一个角的补角是这个角的余角的4倍,求这个角
的度数.
解:设这个角为x度,
则这个角的余角是(90-x)°,
补角是(180-x) °
由题意得,
180-x = 4(90-x)
解得:x = 60
这个角的度数为60°.
17
18
6.已知∠A的余角是它的2倍,求∠A的度数。
7.已知∠B是它补角的3倍,求∠B的度数。
6.解:设∠A为x°,则它的余角为(2x)°,得
X+2x=90,x=30°
答:∠A是30°。
7.解:设∠B为x°则它的补角为(180-x)°得
X=3(180-x), x=135
答:∠B是135°。
练
习
19
8 如图,O是直线AB上的一点,OC平分∠AOB,∠DOE=90o,则
(1)∠2=∠( ),∠1=∠( )
(2)图中,互为余角的角共有哪几对?
( )
(3)图中,∠DOB的补角是 。
4
3
∠1与∠2,∠1与∠4,∠2与∠3,∠4与∠3
∠1,∠3
A
1
4
3
2
B
C
D
E
O
F
(4)延长EO到F,∠COF与∠ BOD的大小关系怎样?
解: ∠COF=∠ BOD
理由:∵ ∠COF+∠ 3=1800
∠ BOD+∠1=1800
又∵∠ 1 = ∠3
∴ ∠COF=∠ BOD
练
习
总
结
(1)余角、补角的概念
注意:余角、补角与两个角的大小有关系,与它们的位置没有关系.
(2)余角、补角的性质
同角(或等角)的余角相等
同角(或等角)的补角相等
20
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
