2021—2022学年人教版九年级数学上册24.1.2 垂直于弦的直径 同步练习题 (word版 含答案)
文档属性
| 名称 | 2021—2022学年人教版九年级数学上册24.1.2 垂直于弦的直径 同步练习题 (word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 192.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 18:05:27 | ||
图片预览


文档简介
2021——2022学年度人教版九年级数学上册 第二十四章
圆 24.1.2 垂直于弦的直径 同步练习题
一、选择题
1.已知AB,CD是⊙O的两条平行弦,AB=8,CD=6,⊙O的半径为5,则弦AB与CD的距离为( )
A.1 B.7 C.4或3 D.7或1
2.的半径为,弦,,,则、间的距离是:( )
A. B. C.或 D.以上都不对
3.已知AB、CD是⊙O的两条弦,AB∥CD,AB=6,CD=8,⊙O的半径为5,则AB与CD的距离是( )
A.1 B.7 C.1或7 D.无法确定
4.如图,⊙O中弦AB长为8,OC⊥AB,垂足为E,若CE=2,则⊙O半径长是( )
A.10 B.8 C.6 D.5
5.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM长的最小值为( )
A.2 B.3 C.4 D.5
6.⊙O的直径AB长为10,弦CD⊥AB于E,将⊙O沿CD翻折,翻折后点B的对应点为点B′,若AB′=6,CB′的长为
( )
A. B.或 C. D.或
7.将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水面AB的宽度是( )cm.
A.6 B. C. D.
8.如图,已知的直径弦于点则下列结论不一定成立的是( )
A. B. C. D.
9.如图,的直径交弦相于点,且若,则的长为( )
A. B. C. D.
10.如图,AB是⊙O的直径,点E是AB上一点,过点E作CD⊥AB,交⊙O于点C,D,以下结论正确的是( )
A.若⊙O的半径是2,点E是OB的中点,则CD=
B.若CD=,则⊙O的半径是1
C.若∠CAB=30°,则四边形OCBD是菱形
D.若四边形OCBD是平行四边形,则∠CAB=60°
二、填空题
11.在平面直角坐标系中,以原点为圆心的圆过点,直线与交于、两点则弦的长最小值为______.
12.已知的半径为5,为圆内的一点,,则过点P的弦长的最小值是________.
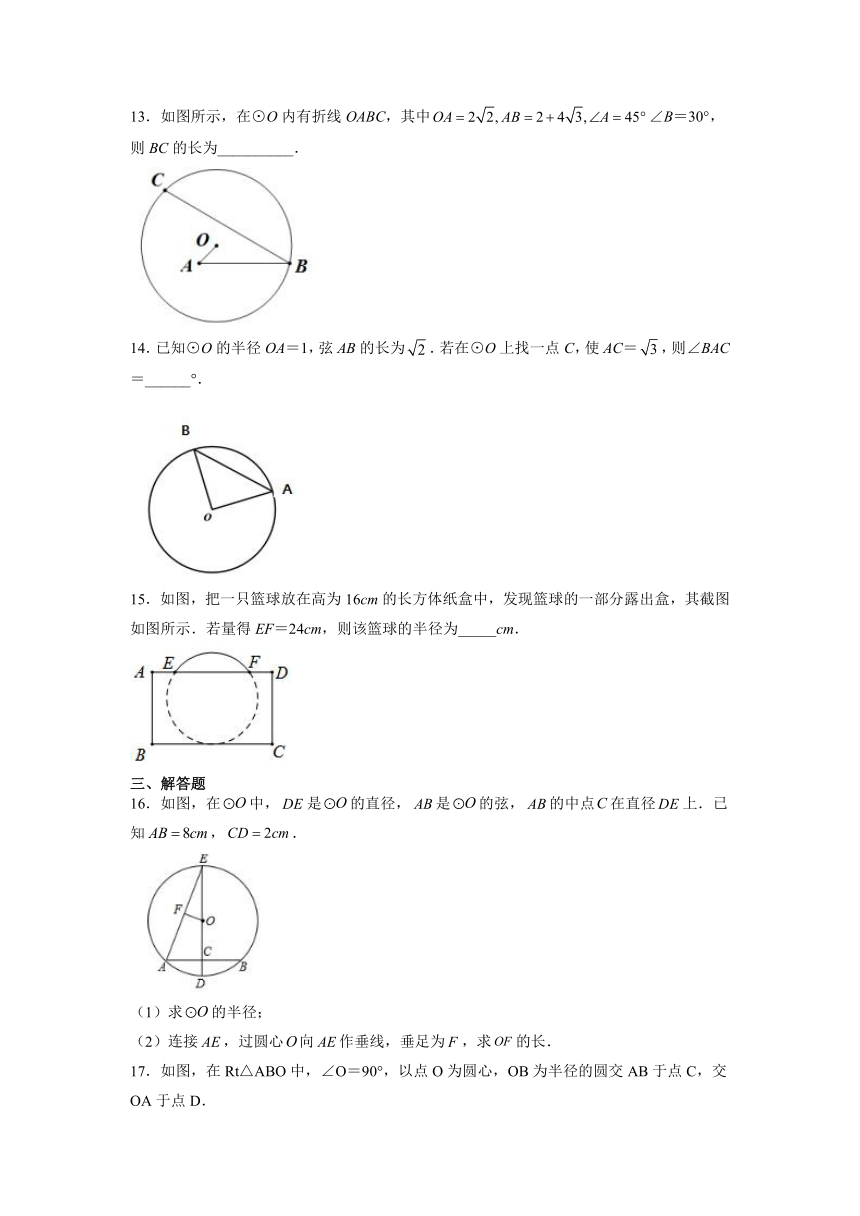
13.如图所示,在⊙O内有折线OABC,其中∠B=30°,则BC的长为__________.
14.已知⊙O的半径OA=1,弦AB的长为.若在⊙O上找一点C,使AC=,则∠BAC=______°.
15.如图,把一只篮球放在高为16cm的长方体纸盒中,发现篮球的一部分露出盒,其截图如图所示.若量得EF=24cm,则该篮球的半径为_____cm.
三、解答题
16.如图,在中,是的直径,是的弦,的中点在直径上.已知,.
(1)求的半径;
(2)连接,过圆心向作垂线,垂足为,求的长.
17.如图,在Rt△ABO中,∠O=90°,以点O为圆心,OB为半径的圆交AB于点C,交OA于点D.
(1)若∠A=25°,则弧BC的度数为 .
(2)若OB=3,OA=4,求BC的长.
18.如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
19.要测量一个钢板上的小孔的直径,通常采用间接的测量方法.如果用一个直径为10 mm的标准钢珠放在小孔上,测得钢珠顶端与小孔平面的距离h = 8 mm(如图),求此小孔的直径d.
20.如图,已知在四边形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O交边DC于E、F两点,AD=1,BC=5,设⊙O的半径长为r.
(1)联结OF,当OF∥BC时,求⊙O的半径长;
(2)过点O作OH⊥EF,垂足为点H,设OH=y,试用r的代数式表示y;
(3)设点G为DC的中点,联结OG、OD,△ODG是否能成为等腰三角形?如果能,试求出r的值;如不能,试说明理由.
21.已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求:
(1)圆心O到AQ的距离;
(2)线段EF的长.
22.如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD=24 m,OE⊥CD于点E.已测得sin∠DOE=.
(1)求半径OD;
(2)根据需要,水面要以每小时0.5m的速度下降,则经过多长时间才能将水排干?
23.如图所示,某地有一座圆弧形的拱桥,桥下水面宽AB为12米,拱高CD为4米.
(1)求这座拱桥所在圆的半径.
(2)现有一艘宽5米,船舱顶部为正方形并高出水面3.6米的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.
【参考答案】
1.D 2.C 3.C 4.D 5.B 6.B 7.C 8.B 9.D 10.C
11.24
12.8
13.14
14.15°或75°
15.12.5
16.(1);(2).
17.(1)50°;(2).
18.(1); (2)存在,
19.d=8mm
20.(1)3;(2)y=;(3)△ODG能成为等腰三角形,r=2
21.(1)即圆心O到AQ的距离为4cm;(2)EF=6cm.
22.10(小时).
23.(1)这座拱桥所在圆的半径为6.5米;(2)货船不能顺利通过这座拱桥.
圆 24.1.2 垂直于弦的直径 同步练习题
一、选择题
1.已知AB,CD是⊙O的两条平行弦,AB=8,CD=6,⊙O的半径为5,则弦AB与CD的距离为( )
A.1 B.7 C.4或3 D.7或1
2.的半径为,弦,,,则、间的距离是:( )
A. B. C.或 D.以上都不对
3.已知AB、CD是⊙O的两条弦,AB∥CD,AB=6,CD=8,⊙O的半径为5,则AB与CD的距离是( )
A.1 B.7 C.1或7 D.无法确定
4.如图,⊙O中弦AB长为8,OC⊥AB,垂足为E,若CE=2,则⊙O半径长是( )
A.10 B.8 C.6 D.5
5.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM长的最小值为( )
A.2 B.3 C.4 D.5
6.⊙O的直径AB长为10,弦CD⊥AB于E,将⊙O沿CD翻折,翻折后点B的对应点为点B′,若AB′=6,CB′的长为
( )
A. B.或 C. D.或
7.将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水面AB的宽度是( )cm.
A.6 B. C. D.
8.如图,已知的直径弦于点则下列结论不一定成立的是( )
A. B. C. D.
9.如图,的直径交弦相于点,且若,则的长为( )
A. B. C. D.
10.如图,AB是⊙O的直径,点E是AB上一点,过点E作CD⊥AB,交⊙O于点C,D,以下结论正确的是( )
A.若⊙O的半径是2,点E是OB的中点,则CD=
B.若CD=,则⊙O的半径是1
C.若∠CAB=30°,则四边形OCBD是菱形
D.若四边形OCBD是平行四边形,则∠CAB=60°
二、填空题
11.在平面直角坐标系中,以原点为圆心的圆过点,直线与交于、两点则弦的长最小值为______.
12.已知的半径为5,为圆内的一点,,则过点P的弦长的最小值是________.
13.如图所示,在⊙O内有折线OABC,其中∠B=30°,则BC的长为__________.
14.已知⊙O的半径OA=1,弦AB的长为.若在⊙O上找一点C,使AC=,则∠BAC=______°.
15.如图,把一只篮球放在高为16cm的长方体纸盒中,发现篮球的一部分露出盒,其截图如图所示.若量得EF=24cm,则该篮球的半径为_____cm.
三、解答题
16.如图,在中,是的直径,是的弦,的中点在直径上.已知,.
(1)求的半径;
(2)连接,过圆心向作垂线,垂足为,求的长.
17.如图,在Rt△ABO中,∠O=90°,以点O为圆心,OB为半径的圆交AB于点C,交OA于点D.
(1)若∠A=25°,则弧BC的度数为 .
(2)若OB=3,OA=4,求BC的长.
18.如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
19.要测量一个钢板上的小孔的直径,通常采用间接的测量方法.如果用一个直径为10 mm的标准钢珠放在小孔上,测得钢珠顶端与小孔平面的距离h = 8 mm(如图),求此小孔的直径d.
20.如图,已知在四边形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O交边DC于E、F两点,AD=1,BC=5,设⊙O的半径长为r.
(1)联结OF,当OF∥BC时,求⊙O的半径长;
(2)过点O作OH⊥EF,垂足为点H,设OH=y,试用r的代数式表示y;
(3)设点G为DC的中点,联结OG、OD,△ODG是否能成为等腰三角形?如果能,试求出r的值;如不能,试说明理由.
21.已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求:
(1)圆心O到AQ的距离;
(2)线段EF的长.
22.如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD=24 m,OE⊥CD于点E.已测得sin∠DOE=.
(1)求半径OD;
(2)根据需要,水面要以每小时0.5m的速度下降,则经过多长时间才能将水排干?
23.如图所示,某地有一座圆弧形的拱桥,桥下水面宽AB为12米,拱高CD为4米.
(1)求这座拱桥所在圆的半径.
(2)现有一艘宽5米,船舱顶部为正方形并高出水面3.6米的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.
【参考答案】
1.D 2.C 3.C 4.D 5.B 6.B 7.C 8.B 9.D 10.C
11.24
12.8
13.14
14.15°或75°
15.12.5
16.(1);(2).
17.(1)50°;(2).
18.(1); (2)存在,
19.d=8mm
20.(1)3;(2)y=;(3)△ODG能成为等腰三角形,r=2
21.(1)即圆心O到AQ的距离为4cm;(2)EF=6cm.
22.10(小时).
23.(1)这座拱桥所在圆的半径为6.5米;(2)货船不能顺利通过这座拱桥.
同课章节目录
