沪科版数学七年级上册 4.3线段的长短比较 课件(共26张ppt)
文档属性
| 名称 | 沪科版数学七年级上册 4.3线段的长短比较 课件(共26张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 14:48:01 | ||
图片预览




文档简介
(共26张PPT)
初中数学沪科版七年级上册第四章第三节《线段的长短比较》
4.3线段的长短比较
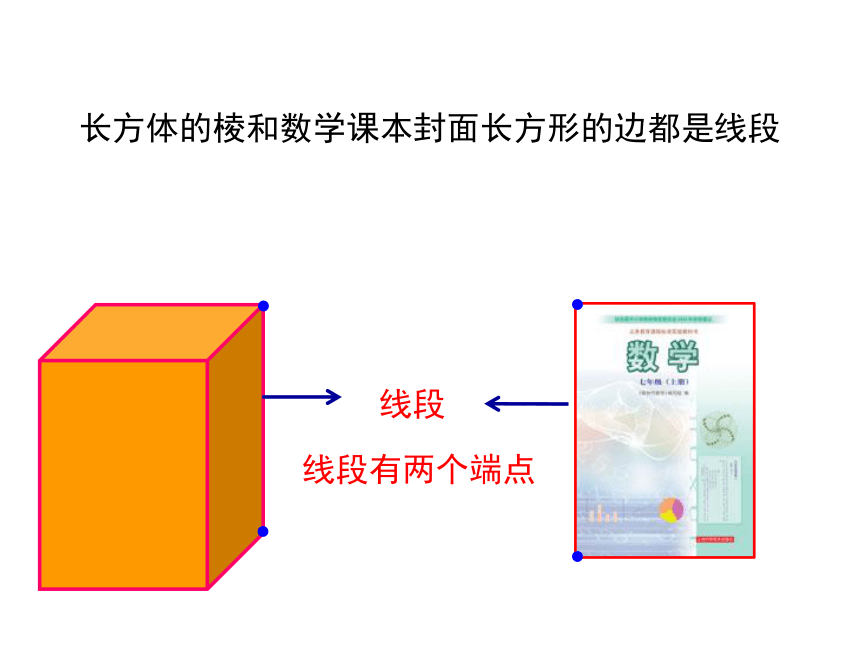
长方体的棱和数学课本封面长方形的边都是线段
线段
线段有两个端点
合作探究
黑板边沿和课桌边沿哪个长?白板边沿和黑板
边沿哪个长?甲同学和乙同学他俩谁的个子高?你是
怎么比较的?
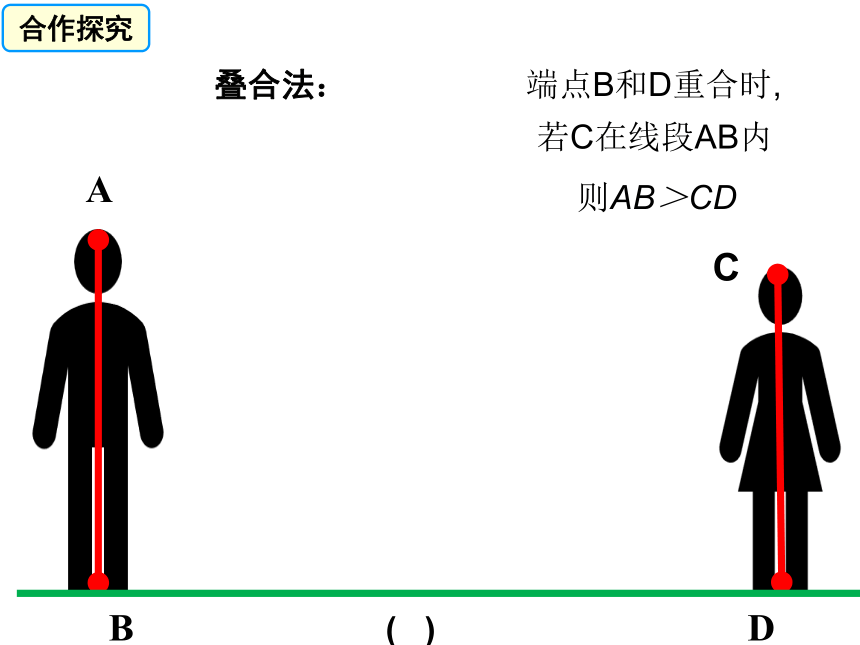
叠合法:
B
A
C
D
则AB>CD
端点B和D重合时,
若C在线段AB内
( )
合作探究
C
D
(A)
B
<
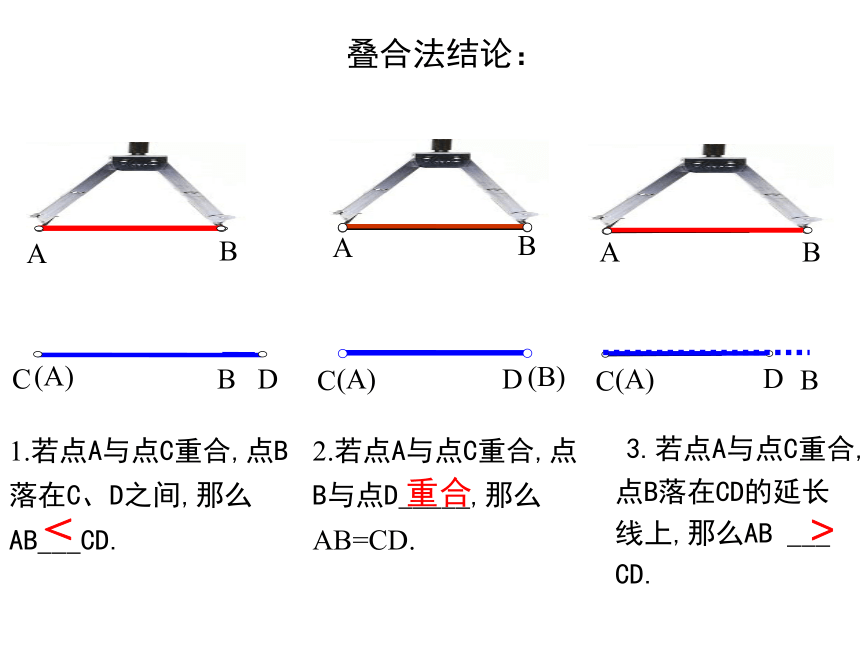
叠合法结论:
B
A
C
(B)
(A)
D
A
B
C
D
B
(A)
B
A
1.若点A与点C重合,点B落在C、D之间,那么AB___CD.
2.若点A与点C重合,点B与点D_____,那么AB=CD.
3.若点A与点C重合,点B落在CD的延长线上,那么AB ___ CD.
重合
>
2、度量法
3、叠合法
——从“数”的角度比较
——从“形”的角度比较
比较线段长短的三种方法
归 纳
1、观察法
合作探究
a
b
A
B
C
已知:点C在线段AB的延长线上,如果AB=a,
线段BC=b.那么AC与AB,BC之间有何关系
记作:AC=AB+BC=a+b
线段AC为线段AB与线段BC的和.
b
a
A
C
B
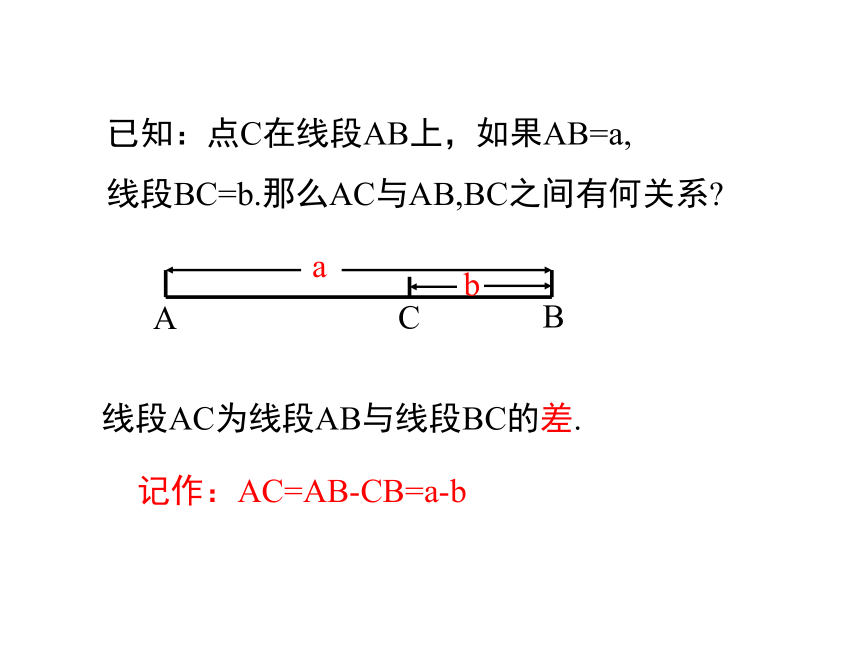
已知:点C在线段AB上,如果AB=a,
线段BC=b.那么AC与AB,BC之间有何关系
线段AC为线段AB与线段BC的差.
记作:AC=AB-CB=a-b
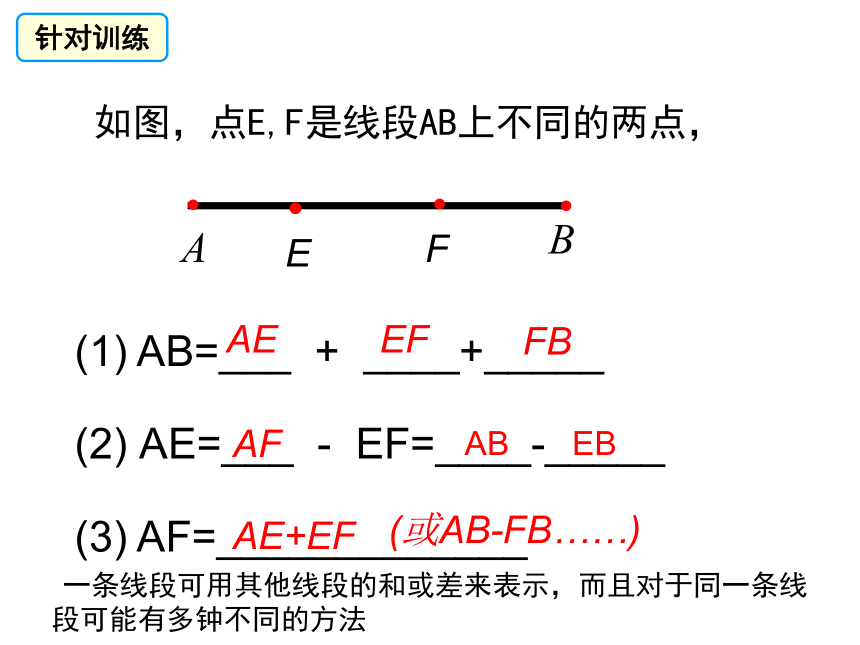
如图,点E,F是线段AB上不同的两点,
B
A
F
E
(1) AB=___ + ____+_____
(2) AE=___ - EF=____-_____
(3) AF=_____________
AF
AE
EF
FB
AE+EF
(或AB-FB……)
AB
EB
针对训练
一条线段可用其他线段的和或差来表示,而且对于同一条线段可能有多钟不同的方法
+ =
A
B
C
AC
CB
AB
AC
>
CB
AC
<
CB
思考:动点C在移动的过程中,
有没有一个位置使得
合作探究
AC=BC
A
B
AC
=
CB
C
点C在线段AB 上且使线段AC,CB相等,这样的点C叫做线段AB的中点。
线段中点定义:
AB
=
AB
AC
=
CB
=
合作探究
A
B
如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你在图上画出最短路线.
发现:两点之间的所有连线中,线段最短
B
A
两点之间的所有连线中,
线段最短.
想一想:
在生活中,我们有哪些实例运用到线段的基本事实?请同学们交流思考一下。
线段的基本事实
归 纳
高 铁
走“捷径“?
B
A
点A与点B之间的距离:
线段AB的长度
点A与点B之间的距离为:
5.8cm
10.8cm
9.3cm
5.8cm
8.7cm
两点之间的距离:两点之间线段的长度
[解析] 在MN上任选一点P1,它到A,B的距离即线段P1A与P1B的长,结合两点之间线段最短可求.
如图所示,直线MN表示一条铁路,铁路两旁各有一点A和B,表示两个工厂.要在铁路上建一货站,使它到两厂距离之和最短,这个货站应建在何处?
解:连接AB,交MN于点P,则这个货站应建在点P处.
P
P1
学以致用
几何画板
例1 已知:线段AB=4 ,延长AB至点C,使AC=11.点D是AB的中点,点E是AC的中点.求DE的长.
几何计算题与小学算术有很大区别。有数学图形语言而没有图形的题,解题时要画出与题意相符合的图,再求解.要求每一步有理有据,先写出图形之间的关系,才能代入数据计算。
典例分析
例2 点A,O,B在一条直线上,线段AO=3,OB=1,C是AO的中点,D是OB的中点.请同学们画出图形,并求线段CD的长.
3
1
1,当点B在线段AO的延长线上
2,当点B在线段AO内
B
C
D
3
1
备注:分类讨论思想
B
D
C
当三个点在同一条直线上时,要注意讨论第三点是在其余两点确定的线段上,还是在线段的延长线上,即要分类讨论。
小 结
例3 如图,B、C 两点把线段AD分成2∶3∶4的三部分,点E是线段AD的中点,EC=2cm,求线段AD的长.
解:设AB=2x,则BC=3x,CD=4x,
由线段的和差,得AD=AB+BC+CD=9x.
由E为AD的中点,得ED= AD= x.
由线段的和差,得CE=DE-CD= x-4x= =2.
解得x=4.
∴AD=9x=36(cm).
在遇到线段之间比的问题时,往往设出未知数,列方程解答简便快捷。
小 结
比较线段的长短
两点之间线段最短
比较线段大小的方法
线段的和、差及中点
度量法
叠合法
整体思想,分类讨论思想,方程思想在求线段长度中的运用
课堂总结
观察法
两点之间的距离
两点之间线段最短
比较线段大小的方法
线段的和、差及中点
度量法
叠合法
观察法
比较线段大小的方法
度量法
叠合法
观察法
比较线段大小的方法
度量法
叠合法
观察法
比较线段大小的方法
度量法
叠合法
观察法
比较线段大小的方法
当堂练习
1.如图,由AB=CD可得AC与BD的大小关系正确的是( )
A.AC>BD B.AC<BD
C.AC=BD D.不能确定
2.已知M是线段AB的中点,①AB=2AM;②BM=1/2AB;③AM=BM;④AM+BM=AB.上面四个式子中,正确的有( )
A.1个 B.2个 C.3个 D.4个
C
D
3.已知线段AB=6 cm,在直线AB上画线段AC=2cm
则BC的长是___________.
4cm或8cm
先画出图形,有两种情况
4.若AB = 6cm,点C是线段AB的中点,点D是线段CB的中点, 求:线段AD的长是多少
5.如图,从A地到B地有三条路①,②,③可走(图中“┍,“┙”,“┕”表示直角),则第________条路最短,另外两条路的长短关系是________.
③
相等
初中数学沪科版七年级上册第四章第三节《线段的长短比较》
4.3线段的长短比较
长方体的棱和数学课本封面长方形的边都是线段
线段
线段有两个端点
合作探究
黑板边沿和课桌边沿哪个长?白板边沿和黑板
边沿哪个长?甲同学和乙同学他俩谁的个子高?你是
怎么比较的?
叠合法:
B
A
C
D
则AB>CD
端点B和D重合时,
若C在线段AB内
( )
合作探究
C
D
(A)
B
<
叠合法结论:
B
A
C
(B)
(A)
D
A
B
C
D
B
(A)
B
A
1.若点A与点C重合,点B落在C、D之间,那么AB___CD.
2.若点A与点C重合,点B与点D_____,那么AB=CD.
3.若点A与点C重合,点B落在CD的延长线上,那么AB ___ CD.
重合
>
2、度量法
3、叠合法
——从“数”的角度比较
——从“形”的角度比较
比较线段长短的三种方法
归 纳
1、观察法
合作探究
a
b
A
B
C
已知:点C在线段AB的延长线上,如果AB=a,
线段BC=b.那么AC与AB,BC之间有何关系
记作:AC=AB+BC=a+b
线段AC为线段AB与线段BC的和.
b
a
A
C
B
已知:点C在线段AB上,如果AB=a,
线段BC=b.那么AC与AB,BC之间有何关系
线段AC为线段AB与线段BC的差.
记作:AC=AB-CB=a-b
如图,点E,F是线段AB上不同的两点,
B
A
F
E
(1) AB=___ + ____+_____
(2) AE=___ - EF=____-_____
(3) AF=_____________
AF
AE
EF
FB
AE+EF
(或AB-FB……)
AB
EB
针对训练
一条线段可用其他线段的和或差来表示,而且对于同一条线段可能有多钟不同的方法
+ =
A
B
C
AC
CB
AB
AC
>
CB
AC
<
CB
思考:动点C在移动的过程中,
有没有一个位置使得
合作探究
AC=BC
A
B
AC
=
CB
C
点C在线段AB 上且使线段AC,CB相等,这样的点C叫做线段AB的中点。
线段中点定义:
AB
=
AB
AC
=
CB
=
合作探究
A
B
如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你在图上画出最短路线.
发现:两点之间的所有连线中,线段最短
B
A
两点之间的所有连线中,
线段最短.
想一想:
在生活中,我们有哪些实例运用到线段的基本事实?请同学们交流思考一下。
线段的基本事实
归 纳
高 铁
走“捷径“?
B
A
点A与点B之间的距离:
线段AB的长度
点A与点B之间的距离为:
5.8cm
10.8cm
9.3cm
5.8cm
8.7cm
两点之间的距离:两点之间线段的长度
[解析] 在MN上任选一点P1,它到A,B的距离即线段P1A与P1B的长,结合两点之间线段最短可求.
如图所示,直线MN表示一条铁路,铁路两旁各有一点A和B,表示两个工厂.要在铁路上建一货站,使它到两厂距离之和最短,这个货站应建在何处?
解:连接AB,交MN于点P,则这个货站应建在点P处.
P
P1
学以致用
几何画板
例1 已知:线段AB=4 ,延长AB至点C,使AC=11.点D是AB的中点,点E是AC的中点.求DE的长.
几何计算题与小学算术有很大区别。有数学图形语言而没有图形的题,解题时要画出与题意相符合的图,再求解.要求每一步有理有据,先写出图形之间的关系,才能代入数据计算。
典例分析
例2 点A,O,B在一条直线上,线段AO=3,OB=1,C是AO的中点,D是OB的中点.请同学们画出图形,并求线段CD的长.
3
1
1,当点B在线段AO的延长线上
2,当点B在线段AO内
B
C
D
3
1
备注:分类讨论思想
B
D
C
当三个点在同一条直线上时,要注意讨论第三点是在其余两点确定的线段上,还是在线段的延长线上,即要分类讨论。
小 结
例3 如图,B、C 两点把线段AD分成2∶3∶4的三部分,点E是线段AD的中点,EC=2cm,求线段AD的长.
解:设AB=2x,则BC=3x,CD=4x,
由线段的和差,得AD=AB+BC+CD=9x.
由E为AD的中点,得ED= AD= x.
由线段的和差,得CE=DE-CD= x-4x= =2.
解得x=4.
∴AD=9x=36(cm).
在遇到线段之间比的问题时,往往设出未知数,列方程解答简便快捷。
小 结
比较线段的长短
两点之间线段最短
比较线段大小的方法
线段的和、差及中点
度量法
叠合法
整体思想,分类讨论思想,方程思想在求线段长度中的运用
课堂总结
观察法
两点之间的距离
两点之间线段最短
比较线段大小的方法
线段的和、差及中点
度量法
叠合法
观察法
比较线段大小的方法
度量法
叠合法
观察法
比较线段大小的方法
度量法
叠合法
观察法
比较线段大小的方法
度量法
叠合法
观察法
比较线段大小的方法
当堂练习
1.如图,由AB=CD可得AC与BD的大小关系正确的是( )
A.AC>BD B.AC<BD
C.AC=BD D.不能确定
2.已知M是线段AB的中点,①AB=2AM;②BM=1/2AB;③AM=BM;④AM+BM=AB.上面四个式子中,正确的有( )
A.1个 B.2个 C.3个 D.4个
C
D
3.已知线段AB=6 cm,在直线AB上画线段AC=2cm
则BC的长是___________.
4cm或8cm
先画出图形,有两种情况
4.若AB = 6cm,点C是线段AB的中点,点D是线段CB的中点, 求:线段AD的长是多少
5.如图,从A地到B地有三条路①,②,③可走(图中“┍,“┙”,“┕”表示直角),则第________条路最短,另外两条路的长短关系是________.
③
相等
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
